Water Cashier Offices Location Optimisation Using Machine

Learning-Based Clustering Approaches: A Case Study of Ordu

Altınordu

Kübra Selvi

, Murat Taşyürek

and Celal Öztürk

Vocational School of Information Technologies, Kayseri University, Kayseri, Turkey

Faculty of Engineering, Arch. and Design, Kayseri University, Kayseri, Turkey

Faculty of Engineering, Erciyes University, Kayseri, Turkey

Keywords: K-Means Clustering, Hierarchical Clustering, Spatial Data.

Abstract: The location of water cashier offices is crucial in terms of both operational efficiency and citizens' easy access

to payment points. This study aims to reduce the average distance covering the widest service area with the

minimum number of cashier offices by using the K-Means and Hierarchical Clustering methods based on the

geographical coordinates of independent sections in Altınordu district of Ordu province. Spatial analyses are

playing an increasingly important role in urban planning, urban transformation and disaster management, and

identifying regions with similar characteristics is of great value. The dataset contains the latitude and longitude

information of the independent sections. The actual number of cashier offices in the Altınordu district of Ordu

province is 3. The optimal number of clusters determined by the Elbow method was 5, while the optimal

number of clusters found using dendrogram analysis was 8. In this context, clustering scenarios of 3, 5, and 8

were examined, and the performance of each algorithm was compared based on the average distance criterion.

The analyses revealed that the K-Means algorithm provided the best average distance. The results demonstrate

that the independent sections in Altınordu can be geographically clustered and that this clustering, taking into

account settlement density and the current cashier distribution, can serve as a guide for cashier planning and

resource allocation. This approach can guide the more effective placement of water cashier offices, thereby

increasing service efficiency and accessibility for citizens.

1 INTRODUCTION

Spatial data mining has become a very challenging

field because large amounts of data are collected in

various applications. The amount of data collected is

increasing exponentially. Therefore, it has gone far

beyond the analytical capabilities of humans.

Recently, clustering has been accepted as the primary

data mining method for information discovery in

spatial databases (Mumtaz & Duraiswamy, 2010).

Today, the effective management of urban

infrastructure and the provision of public services that

are more accessible to citizens are increasing the

importance of spatial data analysis. In this context,

water cashier offices stand out as service points where

citizens can meet their basic needs, such as paying

https://orcid.org/0009-0007-4063-6854

https://orcid.org/0000-0001-5623-8577

https://orcid.org/ 0000-0003-3798-8123

water bills and carrying out subscription procedures.

Similar studies have been conducted in the literature

for different locations. Özmerdivenli and colleagues

identified the best location for a religious facility

using the K-Means clustering algorithm. In their

study, the researchers examined the K-Means

clustering algorithm, which is widely used for

density-based analyses, and highlighted the

limitations of the traditional two-dimensional K-

Means method. To overcome these limitations, they

developed a multi-dimensional K-Means model that

takes into account both spatial distance and

population density, and experimentally compared the

success of the proposed model on real data

(Özmerdivenli et al., 2021). Another study in this

field was presented to the literature by Yürük and

278

Selvi, K., Tasyürek, M. and Öztürk, C.

Water Cashier Ofﬁces Location Optimisation Using Machine Learning-Based Clustering Approaches: A Case Study of Ordu Altınordu.

DOI: 10.5220/0014363700004848

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Advances in Electrical, Electronics, Energy, and Computer Sciences (ICEEECS 2025), pages 278-286

ISBN: 978-989-758-783-2

Erdoğmuş. Yürük and his colleague calculated the

biogas production potential based on the number of

large livestock, small livestock and poultry in Düzce.

In addition, they aimed to determine the optimal

location for a biogas plant using the K-Means

clustering algorithm, thereby identifying the most

suitable areas for waste management and energy

production (Yürük & Erdoğmuş, 2015). George and

his colleagues introduced a study to the literature

showing how the K-Means clustering algorithm can

be used to obtain information about housing

preferences and city services. They examined the

potential of analysing geographical location data

using clustering techniques to improve the quality of

life and find accommodation for expatriates and

general residents in a particular city (George et al.,

2023). In another study, Özmen and colleagues

examined central cashier offices location selection

and ATM inventory management policies with the

aim of optimising Türkiye İş Bankası's cash

management system. The goal was to increase

customer satisfaction by reducing operational costs

and idle cash costs. In this context, mathematical

models were developed for cashier offices locations,

armoured vehicle planning, and ATM cash loading

policies, and tested using data from the Eastern Black

Sea Region. Using a coordinated replenishment

model and clustering methods, they achieved a total

cost reduction of approximately 36% in the system

(Özmen et al., 2015). In Brimicombe's study, in order

to identify clusters in spatial data, he first identifies

spatial concentrations using a ‘hot spot’ clustering

method such as Geo-ProZones and proposes initial

cluster centres and the number of k for K-Means

clustering. then producing a spatial and attribute-

based segmentation from this K-Means clustering

(Brimicombe, 2007). Anderson et al.'s study

presented a two-stage methodology that uses

Geographic Information Systems (GIS) and Kernel

Density Estimation (KDE) to identify spatial

concentrations in order to determine hot spots for

traffic accidents, and then classifies these points using

environmental and qualitative data through the K-

Means clustering algorithm (Anderson, 2009). Güner

and his colleagues examined 525 traffic accidents

involving public transport vehicles in Sakarya

between 2006 and 2012. The accidents, analysed

using the K-Means clustering method, were divided

into two main groups: ‘collisions with other vehicles’

and ‘collisions with pedestrians’. It was found that

most of the accidents occurred during the day, in open

areas, and at intersections without traffic lights. As a

result, it was recommended that traffic lights be

installed at intersections, particularly in side streets

(Güner et al.). In Özdoğan's study, a new cross-

sectional model was developed using the K-Means

clustering algorithm on point cloud data obtained

from a terrestrial laser scanner, in order to identify

deformations occurring underground. Deformation

analyses conducted with the developed model

provided more accurate and reliable results compared

to traditional meshing methods. This approach

enables more precise analysis, especially in cases

where data is incomplete or contains errors (Özdoğan,

2019). Khalid and others examine the impact of big

data analytics on decision-making processes in the

logistics sector and, in particular, use the K-Means

algorithm to cluster data. By analysing supply chain

data using the K-Means clustering method, they have

contributed to operational efficiency and strategic

decision-making processes. The results demonstrate

that the correct use of big data analytics can provide

a competitive advantage in logistics (Khalid &

Herbert-Hansen, 2018). Razavi and his colleagues

propose a low-complexity floor estimation method

for indoor positioning in multi-storey buildings. To

reduce the disadvantages of traditional fingerprint-

based methods, such as large data size and processing

load, despite their high accuracy, they suggest using

the K-Means clustering algorithm to transmit only

cluster heads to mobile devices. In experiments using

real building data, this method significantly reduced

both data size and processing time while delivering

results very close to those of the fingerprint method

in terms of accuracy (Razavi et al., 2015). In

Costanzo's study, a "constrained K-Means" clustering

algorithm is proposed, which considers both

statistical similarities and spatial neighborhood

relationships in the classification of geographic units.

The developed method is specifically designed to

divide regions defined by socio-economic data into

homogeneous groups while ensuring spatial

continuity of these groups. The proposed algorithm

was successfully applied in the regional planning of

Italy’s Calabria and Puglia regions, producing more

meaningful spatial segmentations compared to the

classical K-Means method (Damiana Costanzo,

2001). The Hierarchical clustering algorithm has been

preferred in many studies, particularly due to its

ability to reveal multi-layered similarities in data

structures. In this context, some studies in the

literature are as follows. Zhu and Guo have provided

a solution to the problem of mapping large-volume

spatial flow data. They noted that traditional methods

lead to information loss and visual clutter. They

developed a Hierarchical clustering method that

considers both the starting and destination points,

aiming to produce simpler and more meaningful maps

Water Cashier Ofﬁces Location Optimisation Using Machine Learning-Based Clustering Approaches: A Case Study of Ordu Altınordu

279

by grouping flows with similar origins and

destinations. The proposed algorithm was designed to

handle large datasets and was successfully applied to

243.850 taxi trips in the city of Shenzhen (Zhu & Guo,

2014). Lamb et al. proposed a new space-time

Hierarchical clustering method that enables the joint

analysis of temporal and spatial points. This method

combines location, time, and attribute similarity to

enable the identification of multi-scale cluster

structures. This approach, which is particularly

effective in motion data, has provided more flexible

and meaningful clustering results in situations where

traditional methods fall short (Lamb et al., 2020). In

the study by Feng and colleagues, Geo-SOM and

Hierarchical clustering methods were integrated to

explore geographic data. The approach facilitates the

visual identification of spatial patterns while

providing an effective analytical tool for decision

support systems (Feng et al., 2014). In this regard,

there are studies in the literature where both methods

are applied together in a complementary manner. In

particular, examples where K-Means and

Hierarchical clustering algorithms are used

sequentially or comparatively to gain a deeper

understanding of the data structure and to validate the

clustering results are noteworthy. Fuchs and

colleagues have examined the three most commonly

used clustering approaches in the tourism field

(Hierarchical clustering, K-Means, and DBSCAN)

along with their theoretical foundations and

demonstrated how these techniques can be applied in

practice using the RapidMiner platform. Through

analyses conducted using visual data obtained from

the Flickr platform, they highlighted the various

applications of clustering algorithms, such as market

segmentation, identification of points of interest, and

classification of tourism behaviours (Fuchs &

Höpken, 2022). Kaushik and Mathur conducted a

comparative analysis of the K-Means and

Hierarchical clustering algorithms, detailing the

fundamental characteristics, strengths, and

weaknesses of each method. Their evaluation focused

on factors such as dataset size, sensitivity to noise,

algorithm performance, and areas of applicability.

They concluded that K-Means offers high

performance on large datasets, whereas Hierarchical

clustering yields higher-quality results for smaller

and more structured datasets (Kaushik & Mathur,

2014). Chehata et al. proposed a new method based

on the Hierarchical K-Means clustering algorithm for

classifying LIDAR data. The method aims to reliably

separate ground points in areas with dense vegetation

and complex topography. Clustering, which is

initiated with a fixed neighbourhood size, progresses

hierarchically to classify ground surface information

within the data more accurately. Additionally, the

accuracy of the classification has been improved

using slope maps and multi-scale analysis, and the

proposed method has demonstrated lower error rates

compared to other common filtering algorithms when

applied to ISPRS datasets (Chehata et al., 2008).

The structure of the study is organised as follows:

In the second section, the theoretical foundations of

the K-Means and Hierarchical clustering algorithms

are presented, and the spatial data set belonging to

Altınordu district of Ordu province, which was used

in the study, is introduced in detail. In the third section,

the experimental findings obtained as a result of the

applications carried out with both clustering

algorithms are presented. In the fourth chapter, the

results are discussed in the context of existing cashier

offices locations and the performance difference

between the two algorithms. Finally, in the fifth

chapter, the results obtained from the study are

evaluated in general, and recommendations for future

research are provided.

2 MATERIALS AND METHOD

In this section, the basic principles and working

principles of the K-Means and Hierarchical clustering

algorithms applied using the current data set will be

discussed in detail.

2.1 Clustering Method

Cluster analysis refers to the process of dividing data

in a data set into different groups according to specific

proximity criteria. Each group formed is called a

“cluster”. In other words, clustering is the separation

of data elements with similar characteristics into

different groups. The elements within a cluster are

similar to each other, while the similarity between

clusters is less (Silahtaroğlu, 2013). Clustering

techniques enable objects or variables to be grouped

into homogeneous and heterogeneous clusters using a

distance matrix (Yılmaz & Patır, 2011). Many

clustering methods are based on calculating the

distances between observed values. Therefore, there

is a need for formulas that calculate the distance

between two points. The most commonly used

distance formula in practice is the Euclidean distance

formula. Let p be the number of variables, i, j = 1,

2, ..., n, and k = 1, 2, ..., p. The Euclidean distance is

calculated as follows: (Yeşilbudak et al., 2011).

ICEEECS 2025 - International Conference on Advances in Electrical, Electronics, Energy, and Computer Sciences

280

𝑑



𝑖,𝑗



= 𝑥



−𝑥











(1)

Clustering methods can be grouped under four

headings: Partitioning Clustering, Hierarchical

clustering, Density-Based Clustering, and Grid-

Based Clustering (Silahtaroğlu, 2013). In this study,

K-Means and Hierarchical clustering methods were

used from among the partitioning clustering methods.

2.1.1 K-Means Clustering Method

K-Means is a typical clustering algorithm widely used

in data mining and is particularly preferred for

clustering large data sets. The K-Means algorithm

was first proposed by MacQueen in 1967. This

algorithm is one of the simplest and most widely used

unsupervised learning algorithms developed to solve

the known clustering problem (Jigui et al., 2008). The

K-Means clustering method is a clustering method

that creates k clusters from a data group containing n

data points, grouping data with similar characteristics

into the same cluster (Kodinariya & Makwana, 2013).

It is a cyclical algorithm that continuously repeats

clusters until the most suitable solution is reached. It

divides the available data into k clusters and separates

the clusters according to their averages (centers). As

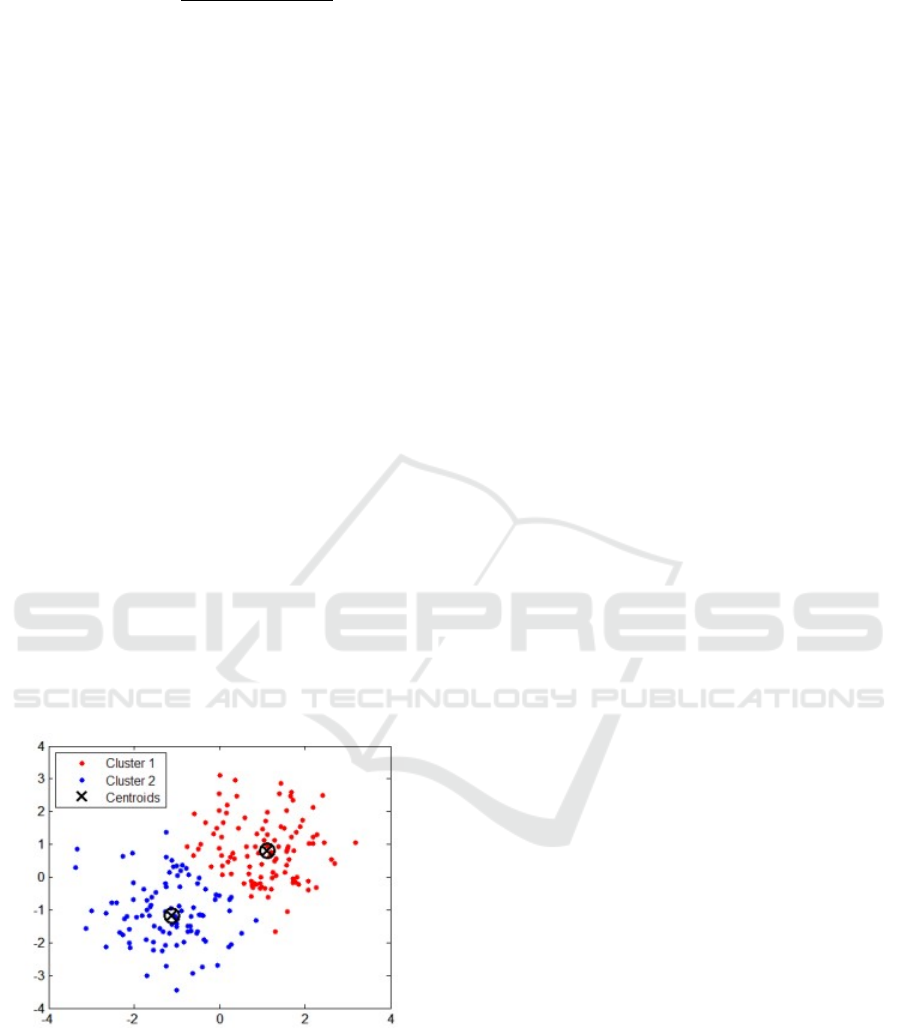
shown in Figure 1, each data point clusters around the

nearest center, and these centers are recalculated in

each iteration. The number of clusters k is determined

by the user (Silahtaroğlu, 2013).

Figure 1: K-Means Clustering (Burkardt, 2009).

The steps of the K-Means clustering algorithm are

listed below (Han et al., 2009):

k: number of clusters

D={t

1, t2,...,tn} : to represent a data group with n

number of elements;

1. The initial average values m

1, m2, ..., mk are

defined for the initially specified sets from the D

data group.

2. Each t

i element is assigned to the set of the closest

3. The average values m1, m2, ..., mk or the clusters

are recalculated.

4. If there is no change in the average m values, the

algorithm is terminated as it has completed its task.

5. If there is a change, the process is repeated from

the first step (step 1).

Determining the value of K is an important issue

in this method. Various methods exist for selecting an

appropriate value of K. One of these is the Elbow

method. This method, used to determine the number

of clusters K, is calculated using the sum of the

squares of the distances of each point to the cluster

centres (WCSS: Within Clusters Sum of Squares).

According to this method, the point where the change

in WCSS decreases is the elbow point, and this elbow

point represents the optimal number of clusters K

(Ketchen & Shook, 1996).

2.1.2 Hierarchical Clustering Method

Hierarchical clustering methods, also known as

linkage methods, are methods that bring units

together at different stages to form sequential clusters

and determine the distance or similarity level at which

elements will be included in these clusters (Doğan,

2008). Hierarchical clustering methods are based on

the principle of treating clusters as a main cluster and

then gradually dividing them into sub-clusters, or

combining clusters that are treated separately into a

cluster in stages (Özkan, 2020). A diagram called a

dendrogram is used to make Hierarchical clustering

results more visually understandable. (Statistics How

To, 2025). A dendrogram can be interpreted by

focusing on the height at which two objects merge. In

Figure 2, E and F are seen to be the most similar

objects, because the height of the link connecting

them is the smallest. The next most similar two

objects are A and B. The height of the dendrogram

indicates the distance between clusters. This diagram

shows that the greatest difference between clusters is

between clusters A and B and clusters C, D, E, and F.

(DisplayR, 2025).

Hierarchical clustering methods are primarily

divided into two main types: Agglomerative

Hierarchical clustering methods and Divisive

Hierarchical clustering methods. In Agglomerative

Hierarchical clustering methods, each observation is

initially considered as an independent cluster, and

then,

in a repetitive manner, each observation or

Water Cashier Ofﬁces Location Optimisation Using Machine Learning-Based Clustering Approaches: A Case Study of Ordu Altınordu

281

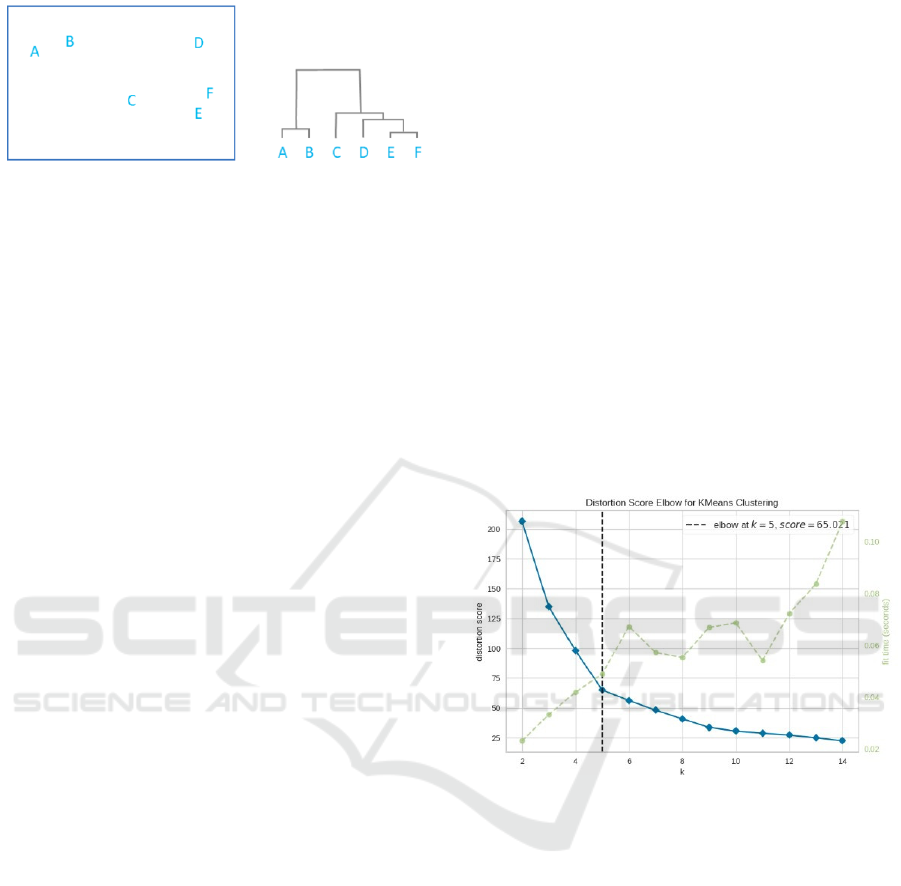
Figure 2: Dendrogram (DisplayR, 2025).

cluster of observations is combined with the

observation or cluster of observations closest to it

until a single cluster containing all observations is

obtained. In divisive Hierarchical clustering methods,

all observations are initially considered as a single

cluster, and then, in a repetitive manner, each

observation or observation cluster is separated from

the observation or observation cluster furthest from it

to form a new cluster until all observations become

independent single clusters (Yeşilbudak et al., 2011).

At each stage of Hierarchical clustering, different

approaches can be applied to determine the two most

similar clusters to be merged using a distance

measure. One such approach is the Ward method. The

centre of a cluster considers the average distance of

the cluster from the examples within it. In other words,

it aims to minimise the total intra-cluster variance. To

this end, it calculates the sum of squared errors using

intra-cluster squared deviations. (Murtagh &

Contreras, 2017).

2.2 Dataset

The data sets used in this study are publicly available

at Ulasav (Ulusal Akıllı Şehir Açık Veri Platformu,

2025). The data sets include independent section data

at the neighbourhood level for Altınordu district in

Ordu province and spatial data in KML format related

to OSKİ (Ordu Water and Sewerage Administration)

cashier offices. At the neighborhood level,

independent section data includes latitude/longitude

information, neighborhood names, and the number of

independent units. Data for Oski cashier offices

include details such as cashier offices locations

(latitude/longitude information), cashier offices

names, and additional cashier offices information

(e.g., operating hours, service types).

3 RESULTS

In this study, K-Means and Hierarchical Clustering

algorithms were used to optimise existing cashier

offices locations and determine new cashier offices

locations in Altınordu district of Ordu province. The

clustering results obtained were evaluated by

comparing the average distances between the

determined cashier offices locations and independent

units. Python software was used to perform the

simulations in this study.

K-Means Clustering Analysis Results: In the K-

Means algorithm, the k value must be determined

before the algorithm is run. However, selecting the

appropriate k value is usually a data-specific decision,

and an incorrect selection can negatively affect the

meaningfulness of the clusters. For this reason, the

Elbow Method is commonly used to determine the

optimal k value. In Figure 3, it can be seen that the

decrease in the distortion score becomes significantly

less pronounced at k=5 (the formation of an ‘elbow’).

This indicates that 5 clusters best represent the dataset

and that adding more clusters would not significantly

increase the benefit gained. The distortion score for

this optimal k value (k=5) is reported as 65.021.

Figure 3: Distortion Score Elbow for K-Means Clustering.

Hierarchical Clustering Analysis Results: The

Ward method was used in the Hierarchical clustering

analysis. The dendrogram visualises the hierarchical

relationship between data points and allows the

number of clusters to be determined by identifying an

appropriate cut-off point. By examining the cluster

structures formed when a cut-off is made at a specific

distance threshold in the dendrogram, the optimal

number of clusters can be determined. In the current

dendrogram, the large vertical lines observed

represent different cluster mergers, and it can be seen

from Figure 4 that a specific cut-off point results in 8

separate clusters.

ICEEECS 2025 - International Conference on Advances in Electrical, Electronics, Energy, and Computer Sciences

282

Figure 4: Hierarchical Clustering Dendrogram (Ward

Method).

The study will compare the results obtained using

different clustering methods. In reality, there are three

OSKİ cashier offices. Analysis using the Elbow

method with the K-Means algorithm found that the

most appropriate number of clusters is five, while

dendrogram analysis using the Ward linkage method

in the hierarchical clustering approach found that the

most appropriate number of clusters is eight. These

three different values were taken into account and

evaluated in the comparative analyses of the study.

Cluster Scenario: The three different clusters

obtained with KMeans (Figure 5) and hierarchical

clustering (Figure 6) the suggested cashier offices

locations for each cluster are visualized.

Figure 5: Recommended Cashier Offices Locations with K-

Means (3 Cluster).

The average distance for K-Means is

approximately 0.046 degrees, while the average

distance for Hierarchical Clustering is determined to

be approximately 0.047 degrees. In this scenario,

while both algorithms exhibit similar performance, the

K-Means algorithm has demonstrated better

performance. The average distance of the actual

cashier offices locations is approximately 0.111

degrees.

This is more than double the algorithm

Figure 6: Recommended Cashier Offices Locations with

Hierarchical Clustering (3 Cluster).

values. The average distances of the actual scale

positions to the independent units determined by the

K-Means and Hierarchical Clustering methods are

compared in Figure 7.

Figure 7: Average Distance Comparison by Methods (3

Cluster).

Cluster Scenario: When the number of clusters is

increased to five, the district is divided into smaller

and more homogeneous areas. This distribution

allows service points to be located closer to

independent units. The five different clusters obtained

with KMeans (Figure 8) and hierarchical clustering

(Figure 9) the suggested cashier offices locations for

each cluster are visualized.

As the number of clusters increases, the average

distances decrease significantly. This value drops to

approximately 0.033 degrees for K-Means and 0.035

degrees for Hierarchical Clustering. In this scenario,

the two algorithms deliver similar results, with K-

Means showing a slight performance advantage.

Figure 10 compares the average distances of the

cashier offices locations to independent units

determined by the K-Means and Hierarchical

Clustering methods.

Water Cashier Ofﬁces Location Optimisation Using Machine Learning-Based Clustering Approaches: A Case Study of Ordu Altınordu

283

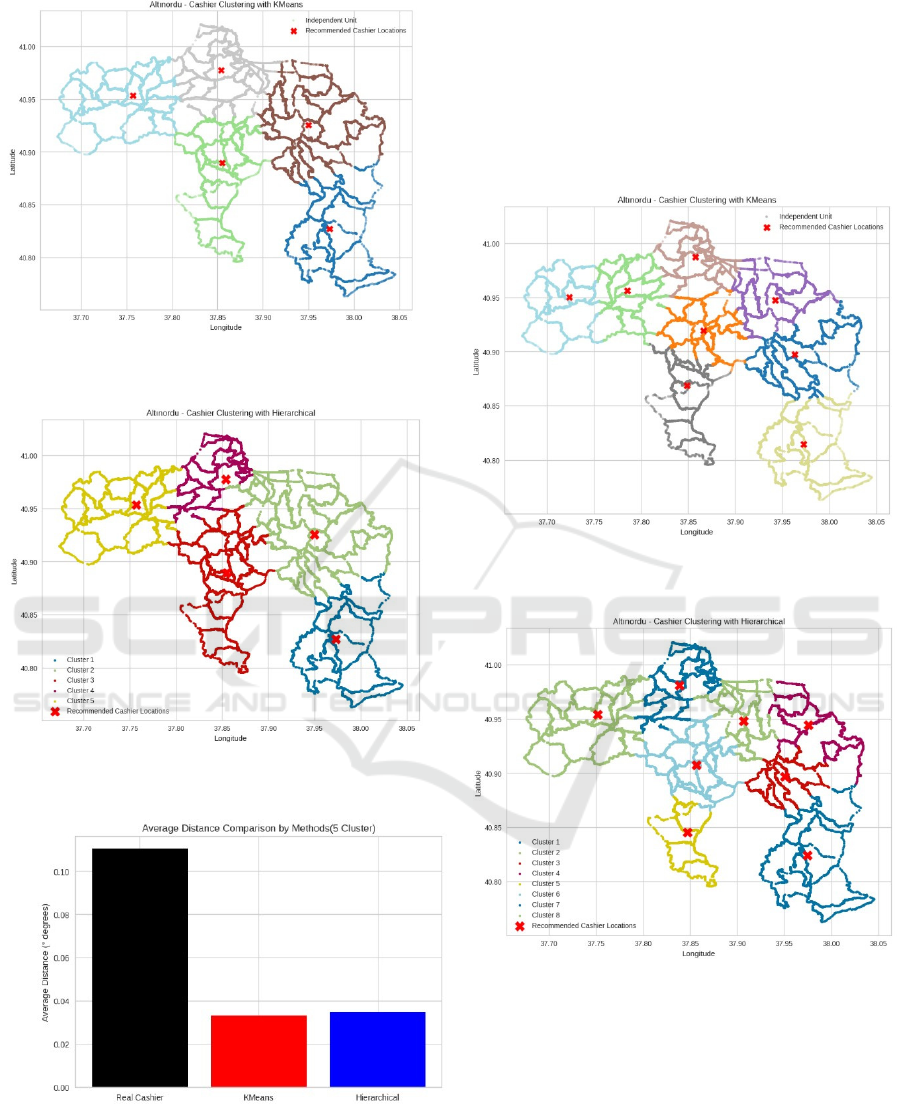
Figure 8: Recommended Cashier Offices Locations with K-

Means (5 Cluster).

Figure 9: Recommended Cashier Offices Locations with

Hierarchical Clustering (5 Cluster).

Figure 10: Average Distance Comparison by Methods (5

Cluster).

Cluster Scenario: Eight clusters have enabled

Altınordu district to be divided into more detailed and

locally based regions. This model aims to maximise

service accessibility. Although K-Means and

Hierarchical Clustering create different geometric

cluster structures, they target density centres by

proposing a cashier offices location for each cluster.

The eight different clusters obtained with KMeans

(Figure 11) and hierarchical clustering (Figure 12) the

suggested cashier offices locations for each cluster

are visualized.

Figure 11: Recommended Cashier Offices Locations with

K-Means (8 Cluster).

Figure 12: Recommended Cashier Offices Locations with

Hierarchical Clustering (8 Cluster)

In this scenario, the lowest average distances were

obtained. The average distance for K-Means was

approximately 0.026 degrees, while the average

distance for Hierarchical Clustering was calculated to

be approximately 0.028 degrees. The actual cashier

offices locations are compared with the average

distances of the cashier offices locations determined

by the K-Means and Hierarchical Clustering methods

to independent units in Figure 13.

ICEEECS 2025 - International Conference on Advances in Electrical, Electronics, Energy, and Computer Sciences

284

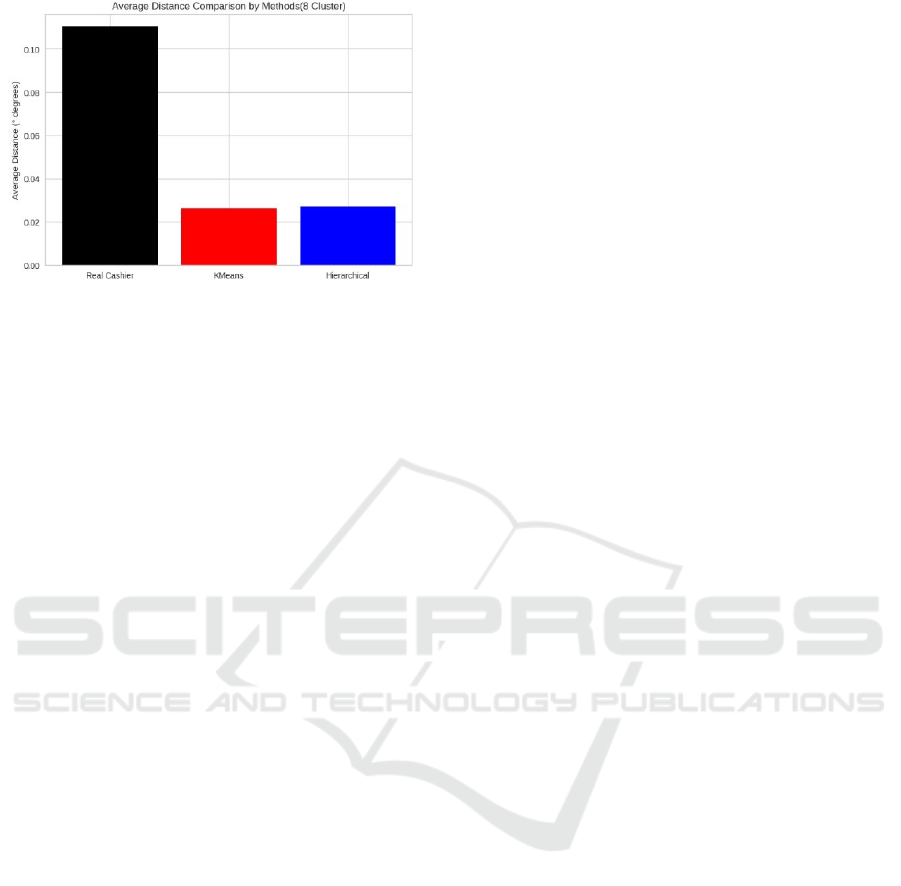
Figure 13: Average Distance Comparison by Methods (8

Cluster).

The actual cashier offices locations have the

highest average distance, approximately 0.11 degrees.

Although the degree distance varies depending on the

location in the geographic coordinate system,

assuming that 1 degree is equal to approximately

111.1 km, this distance corresponds to approximately

12.2 km. This indicates that the current cashier

locations are relatively further away than the general

independent units and have potential for

improvement in terms of accessibility.

Both K-Means and Hierarchical clustering

methods provide significantly lower average

distances compared to actual cashier offices locations.

K-Means, by exhibiting a lower average distance

value compared to Hierarchical Clustering, has

provided a more optimal distribution in terms of

access to cashier offices. This demonstrates that K-

Means can cluster the geographical distribution of

independent units in Altınordu district more

effectively, thereby placing cashier offices locations

closer to independent units.

4 DISCUSSION

The results obtained clearly demonstrate that the K-

Means and Hierarchical clustering algorithms are

effective tools for optimising cashier offices locations

in Altınordu district of Ordu province. Both methods

significantly reduce the average distance to

independent units compared to the current cashier

offices locations. In particular, K-Means clustering

appears to be more advantageous in terms of its

potential to increase the accessibility of cashier

offices services, as it yields a lower average distance

value. In this regard, it is recommended to evaluate

the cashier offices location ns determined by

clustering methods to make cashier offices services in

Altınordu district more efficient and accessible. In

particular, the 8-cluster distribution obtained with K-

Means clustering algorithm could form the basis for a

more detailed service area plan. In future studies,

including additional factors such as demographic data,

existing infrastructure, and operational costs in

cashier offices location optimisation could provide

more comprehensive and practically applicable

solutions.

5 CONCLUSIONS

In this study, spatial density zones were determined

using the K-Means and Hierarchical Clustering

algorithms based on the geographical location data of

independent sections in Altınordu district, Ordu

province. The aim is to ensure more efficient

placement of water cashier offices and provide easier

access for citizens. The clusters obtained were

compared with the locations of the existing three

water cashier offices to analyse regional similarities

and homogeneous areas. In the analysis, the optimal

number of clusters for K-Means was determined as 5

using the Elbow method, and these 5 cluster centres

were proposed as potential water cashier offices

locations. Hierarchical Clustering (Ward method)

grouped the data set into 8 different clusters. This

analysis compares the performance of the K-Means

and Hierarchical Clustering algorithms for the

optimisation of cashier offices locations using the

independent section KML data of Altınordu district in

Ordu province, based on different cluster numbers (3,

5, 8). The effectiveness of the cashier offices

locations proposed by both clustering algorithms was

evaluated based on the average distances to

independent units. The results clearly show that the

average distance of the existing actual cashier offices

locations is significantly higher than that of the

locations proposed by the clustering methods. This

confirms that the existing locations are not optimised

in terms of accessibility. The results indicate that

these methods could make important contributions to

urban planning and the efficiency of public services.

It was observed that the cashier offices locations

obtained using the K-Means method provided a more

efficient distribution by offering a lower average

distance value compared to the Hierarchical

Clustering method. These results highlight the

potential and benefits of using machine learning

algorithms in the spatial planning of public and

private sector service units. Future studies could

develop more comprehensive and realistic solutions

Water Cashier Ofﬁces Location Optimisation Using Machine Learning-Based Clustering Approaches: A Case Study of Ordu Altınordu

285

by enriching these placement models with additional

variables such as road networks and operational costs.

REFERENCES

Anderson, T. K. (2009). Kernel density estimation and K-

means clustering to profile road accident hotspots.

Accident Analysis & Prevention, 41(3), 359–364.

Brimicombe, A. J. (2007). A dual approach to cluster

discovery in point event data sets. Computers,

environment and urban systems, 31(1), 4–18.

Burkardt, J. (2009). K-means clustering. Virginia Tech,

Advanced Research Computing, Interdisciplinary

Center for Applied Mathematics, 5.

Chehata, N., David, N., & Bretar, F. (2008). LIDAR data

classification using hierarchical K-means clustering.

ISPRS Congress Beijing 2008,

Damiana Costanzo, G. (2001). A constrained k-means

clustering algorithm for classifying spatial units.

Statistical Methods and Applications, 10(1), 237–256.

DisplayR. (2025). https://www.displayr.com/what-is-

dendrogram/

Doğan, B. (2008). Bankaların gözetiminde bir araç olarak

kümeleme analizi: Türk bankacılık sektörü için bir

uygulama

Feng, C. C., Wang, Y. C., & Chen, C. Y. (2014). Combining

Geo ‐ SOM and hierarchical clustering to explore

geospatial data. Transactions in GIS, 18(1), 125–146.

Fuchs, M., & Höpken, W. (2022). Clustering: hierarchical,

k-means, DBSCAN. In Applied Data Science in

Tourism: Interdisciplinary Approaches,

Methodologies, and Applications (pp. 129–149).

Springer.

George, S., Seles, J. K. S., Brindha, D., Jebaseeli, T. J., &

Vemulapalli, L. (2023). Geopositional Data Analysis

Using Clustering Techniques to Assist Occupants in a

Specific City. Engineering Proceedings, 59(1), 8.

Güner, S., Geçer, H. S., & Coşkun, E. Toplu Taşima

Araçlarinin Dâhil Olduğu Trafik Kazalarinin K-

Ortalamalar Kümeleme Algoritmasi İle Analizi:

Sakarya Uygulamasi.

Han, J., Lee, J.-G., & Kamber, M. (2009). An overview of

clustering methods in geographic data analysis.

Geographic data mining and knowledge discovery, 2,

149–170.

Jigui, S., Jie, L., & Lianyu, Z. (2008). Clustering algorithms

research. Journal of software, 19(1), 48–61.

Kaushik, M., & Mathur, B. (2014). Comparative study of

K-means and hierarchical clustering techniques.

International Journal of Software & Hardware

Research in Engineering, 2(6), 93–98.

Ketchen, D. J., & Shook, C. L. (1996). The application of

cluster analysis in strategic management research: an

analysis and critique. Strategic management journal,

17(6), 441–458.

Khalid, W., & Herbert-Hansen, Z. N. L. (2018). Using k-

means clustering in international location decision.

Journal of Global Operations and Strategic Sourcing,

11(3), 274–300.

Kodinariya, T. M., & Makwana, P. R. (2013). Review on

determining number of Cluster in K-Means Clustering.

International Journal, 1(6), 90–95.

Lamb, D. S., Downs, J., & Reader, S. (2020). Space-time

hierarchical clustering for identifying clusters in

spatiotemporal point data. ISPRS International Journal

of Geo-Information, 9(2), 85.

Mumtaz, K., & Duraiswamy, K. (2010). An analysis on

density based clustering of multi dimensional spatial

data. Indian Journal of Computer Science and

Engineering, 1(1), 8–12.

Murtagh, F., & Contreras, P. (2017). Algorithms for

hierarchical clustering: an overview, II. Wiley

Interdisciplinary Reviews: Data Mining and

Knowledge Discovery, 7(6), e1219.

Özdoğan, M. V. (2019). Yeraltı deformasyonlarının

belirlenmesi amacıyla K-ortalamalar kümeleme

algoritması kullanılarak kesit model geliştirilmesi.

Dokuz Eylül Üniversitesi Mühendislik Fakültesi Fen ve

Mühendislik Dergisi, 21(63), 707–717.

Özkan, Y. (2020). Veri madenciliği yöntemleri. Papatya

Yayıncılık Eğitim.

Özmen, M., Tunç, S., Yağız, G., Yıldırım, S., Yıldız, E.,

Köksalan, M., & Gürel, S. (2015). Merkezi Vezne Yer

Seçimi Ve Atm Envanter Yönetim Politikalari İle Nakit

Yönetim Sistemi Optimizasyonu. Endüstri

Mühendisliği, 26(2), 4–20.

Özmerdivenli, N. M., Taşyürek, M., & Daşbaşı, B. (2021).

Dini Tesis Yapılacak En İyi Konumun K-means

Kümeleme Yöntemleri ile Tespit Edilmesi. Avrupa

Bilim ve Teknoloji Dergisi(32), 424–430.

Razavi, A., Valkama, M., & Lohan, E.-S. (2015). K-means

fingerprint clustering for low-complexity floor

estimation in indoor mobile localization. 2015 IEEE

Globecom Workshops (GC Wkshps),

Silahtaroğlu, G. (2013). Veri madenciliği: Kavram ve

algoritmaları. Papatya.

Statistics How To. (2025).

https://www.statisticshowto.com/hierarchical-

clustering/

Ulusal Akıll

ı Şehir Açık Veri Platformu. (2025).

https://ulasav.csb.gov.tr/

Yeşilbudak, M., Kahraman, H., & Karacan, H. (2011). Veri

madenciliğinde nesne yönelimli birleştirici hiyerarşik

kümeleme modeli. Gazi Üniversitesi Mühendislik

Mimarlık Fakültesi Dergisi, 26(1).

Yılmaz, Ş. K., & Patır, S. (2011). Kümeleme Analizi Ve

Pazarlamada Kullanimi. Akademik Yaklaşımlar

Dergisi, 2(1), 91–113.

Yürük, F., & Erdoğmuş, P. (2015). Düzce ilinin hayvansal

atiklardan üretilebilecek biyogaz potansiyeli ve k-

means kümeleme ile optimum tesis konumunun

belirlenmesi. İleri Teknoloji Bilimleri Dergisi, 4(1), 47–

56.

Zhu, X., & Guo, D. (2014). Mapping large spatial flow data

with hierarchical clustering. Transactions in GIS, 18(3),

421–435.

ICEEECS 2025 - International Conference on Advances in Electrical, Electronics, Energy, and Computer Sciences

286