A Monte Carlo Study of Integrating Discrete Choice Models and

Neural Networks in Transportation Decision-Making

Fuming Zhang

Business School, University of Shanghai for Science and Technology, Shanghai, China

Keywords: Hybrid Discrete Choice Model, Neural Network with Attention, Multinomial Logit (MNL), Monte Carlo

Simulation, Travel Behavior Modeling.

Abstract: With the rapid development of urban transportation systems and the increasing diversity of residents' travel

behaviors, accurately modeling individuals' choice behaviors among different travel modes has become an

important topic in traffic behavior research. The traditional multinomial Logit (MNL) discrete choice model

is widely used in travel decision modeling due to its simple structure and good interpretability. However, the

MNL model has certain limitations when dealing with nonlinear preference relations and behavioral

heterogeneity. To this end, this paper proposes a hybrid discrete choice model (HDCM) framework that

integrates neural networks (NNs) and attention mechanisms. On the basis of retaining the interpretability of

variables, the HDCM enhances the expression ability of complex behavioral patterns. This paper evaluates

the model performance by constructing simulation data containing standard normal explanatory variables and

conducting Monte Carlo experiments. The experimental results show that the HDCM outperforms the MNL

model and the pure NN model in terms of parameter estimation accuracy, error indicators (mean squared error

(MSE), mean absolute error (MAE)), and confidence interval coverage, demonstrating stronger stability and

adaptability. This research provides a more flexible and effective analytical tool for modeling complex travel

decision-making behaviors and has a promising application prospect.

1 INTRODUCTION

In the field of travel behavior modeling, the Discrete

Choice Model (DCM) is widely used to describe the

choice decision-making process of individuals among

multiple transportation modes, especially the

Multinomial Logit model (MNL) (Wong & Farooq,

2021; Hausman & McFadden, 1984). It has become

the mainstream of research because of its simple

derivation, efficient estimation and clear economic

implications of parameters. However, the traditional

MNL, based on the setting of a linear utility function

and the assumption of independent independence

(IIA), shows certain limitations when dealing with the

nonlinear preferences, diverse behavioral

characteristics, and individual heterogeneity reflected

in real traffic decisions, and is difficult to capture the

complex logic of human behavior (Bourguignon et

al., 2007; Kashifi et al., 2022).

In recent years, with the rapid development of

deep learning technology, neural networks (NNs)

https://orcid.org/0009-0000-5929-8735

have gained extensive attention in travel behavior

modeling due to their powerful nonlinear expression

capabilities (Omrani, 2015; Wang & Ross, 2018).

Their flexible structure helps to depict complex

behavioral response patterns, but it also faces

problems such as difficult parameter interpretation

and unclear behavioral inference (Li et al., 2010;

Bhat, 2003). To integrate the advantages of both, this

paper proposes a multi-Logit hybrid model

framework that introduces an attention mechanism

NN, which enhances the nonlinear fitting ability of

the Logit model while maintaining its interpretability.

The main contributions of this paper include: (1)

Constructing a hybrid modeling structure that is both

interpretable and flexible; (2) The effectiveness of it

in nonlinear decision modeling was verified through

systematic experiments, providing a new

methodological basis and practical reference for the

modeling of transportation mode selection.

522

Zhang, F.

A Monte Carlo Study of Integrating Discrete Choice Models and Neural Networks in Transportation Decision-Making.

DOI: 10.5220/0014362200004718

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 522-526

ISBN: 978-989-758-792-4

2 MODEL ARCHITECTURE

2.1 Overall Model Framework

Based on the traditional MNL model, this paper

integrates NNs and attention mechanisms to propose

a hybrid discrete selection model for transportation

mode selection, aiming to better describe the

nonlinear characteristics and individual differences in

travel behavior (Krishnapuram et al., 2005).

The model structure is shown in Figure 1, it first

sets the real parameter matrix to generate simulation

data containing constant terms and two standard

normal explanatory variables. For each non-reference

option, an independent neural network is constructed,

with a structure consisting of an attention layer and

two fully connected networks, and the selection

probability is calculated through the Softmax

function. Subsequently, 100 rounds of simulation

experiments were conducted, and the MNL model

was used for parameter estimation. The model

performance was evaluated through indicators such

as deviation, mean squared error (MSE), mean

absolute error (MAE), T-statistic, and confidence

interval coverage. The results show that this method

enhances the modeling ability of nonlinear

relationships while retaining interpretability.

Figure 1: Architecture of the Hybrid Discrete Choice Model with Attention-Based Neural Networks. (Picture credit: Original)

2.2 Design of Neural Network-Based

Utility Function

In this paper, NN with an attention mechanism is

adopted to conduct nonlinear modeling of the utility

function. Each alternative corresponds to an

independent network, which includes an input layer,

an attention layer, two hidden layers (64 RELU-

activated neurons in each layer), and an output layer.

During the training process, the MSE is adopted

as the loss function, the optimizer is Adam, the

learning rate is set at 0.01, and each round of

experimental training is conducted 1000 times. This

structure enhances the model's ability to fit complex

behavioral patterns while retaining the importance of

explanatory variables, providing greater flexibility

for travel choice modeling.

2.3 Monte Carlo Simulation Procedure

To verify the estimation performance of the discrete

selection model based on NNs, an MC simulation

experiment is designed in this paper (Keane &

Wolpin, 1994). Data generation is based on multiple

Logit Settings. The workflow of the Monte Carlo

Simulation is shown in Figure 2. Individuals choose

among three options, and the utility of each option is

modeled by an NN containing three explanatory

variables (including intercept terms). Set the real

parameters to a fixed matrix and the sample size to

In each round of simulation, the input

variable X (N × K) is generated. The utility is

calculated using an NN and the selection probability

is obtained through Softmax to generate the selection

result y. Data does not require missing processing.

Preprocessing includes feature normalization and

format conversion to adapt to NNs and Logit models.

A Monte Carlo Study of Integrating Discrete Choice Models and Neural Networks in Transportation Decision-Making

523

Figure 2: Workflow of the Monte Carlo Simulation for the

Hybrid Discrete Choice Model. (Picture credit: Original)

3 DATASET AND EXPERIMENTS

3.1 Dataset

To verify the estimation performance of the discrete

selection model based on NN, this paper designs a

Monte Carlo experiment based on multiple Logit

Settings. Each individual makes a choice among three

travel options, and the utility of each option is

estimated by an independent NN. The input contains

three explanatory variables. The real parameters are

set to a fixed matrix, and the sample size is set to

1000.

In each round of simulation, an input variable

matrix X∈R

×

(N  1000，K3). The utility of

each option is calculated through NN, and the

selection probability is generated in combination with

the Softmax function. Then, the selection result is

obtained through a probability simulation.

The simulation data does not require missing

value processing. The main preprocessing step is

feature normalization to adapt to the NN training and

multiple Logit model estimation processes.

3.2 Experimental Setup

This study conducted experiments on a local

computer. The operating environment was Windows

11, equipped with an NVIDIA GeForce RTX 4080

notebook GPU, an Intel64 architecture processor, and

34GB of memory (18GB is available), as summarized

in Table 1. The experiment was mainly programmed

using Python 3.12 (partially 3.10), and the core

dependent libraries are also listed in Table 1.

The neural network structure consists of two fully

connected MLP layers (64 neurons per layer, ReLU

activated), with a separate network trained for each

non-reference option and an attention mechanism to

weight the input features. The training strategy is

detailed in Table 2.

The Monte Carlo experiment generates 1,000

samples in each round and repeats for 100 rounds.

Simulation settings are shown in Table 3. Parameter

estimation is conducted using the MNLogit model in

the statsmodels library for maximum likelihood

estimation. The evaluation metrics include MSE,

MAE, bias, and 95% confidence interval coverage.

Table 1. Runtime Environment and Core Library

Versions.

Com

onent Descri

tion

Operating

System

Windows 11

CPU

Intel64 Family 6 Model 183

(AMD64 architecture)

GPU

NVIDIA GeForce RTX 4080

GPU

Memory 34.08 GB total, 18.07 GB available

Programming

Lan

Python 3.12 (some experiments

run in 3.10

)

Core Libraries

PyTorch 2.0, statsmodels 0.14,

numpy 1.24, seaborn 0.12, pandas,

mat

lotlib

Table 2: Neural Network Training Settings.

Item Configuration

Network Structure

Two-layer MLP, 64 neurons per

Activation

Function

ReLU

Attention

Mechanism

Applied to input features of each

option

Loss Function MSE

timize

Adam, learnin

rate = 0.01

Number of

Networks

2 (one for each non-reference

alternative)

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

524

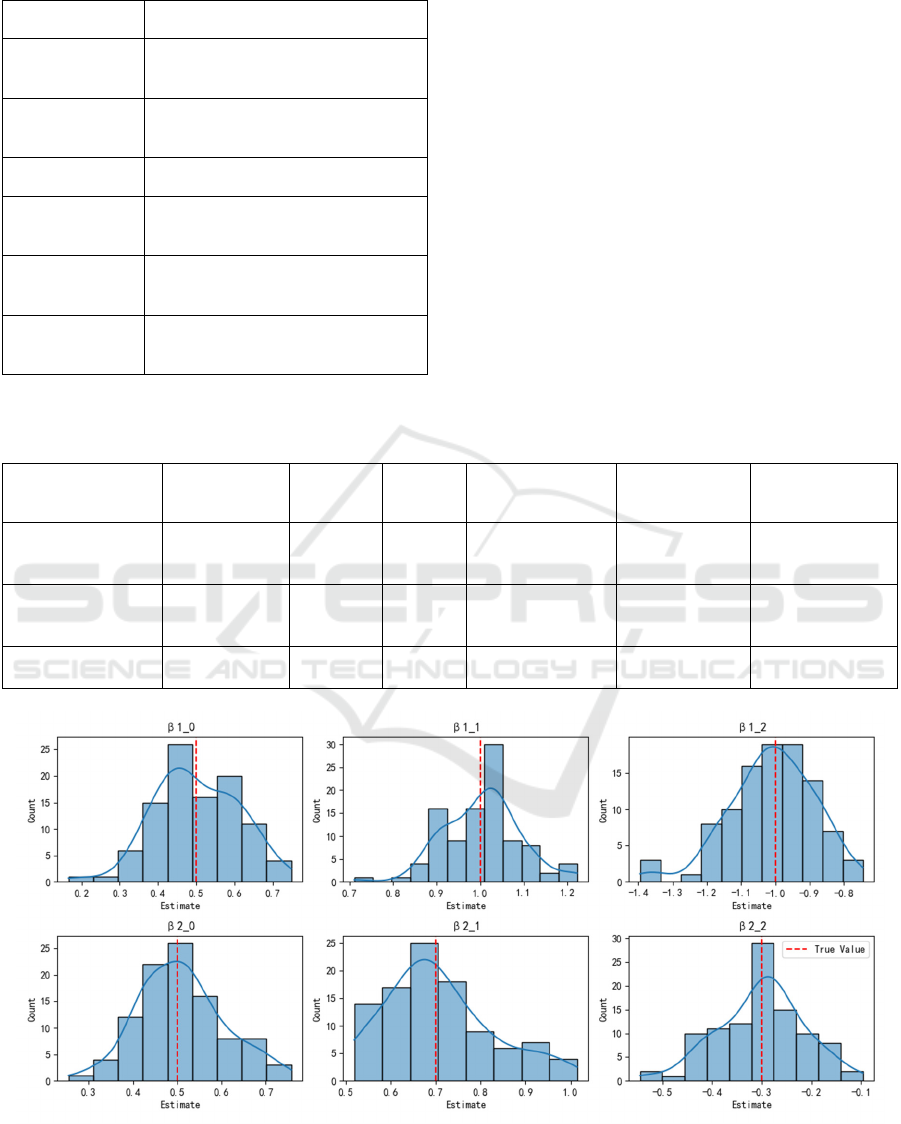
Table 3: Monte Carlo Simulation Settings.

Item Descri

tion

Sample Size (N)

1000 individuals per simulation

roun

Number of

Choices

(

)

Repetitions (R) 100 simulation rounds

Simulation

Process

New data generation and MNLogit

estimation each roun

Estimation

Metho

Multinomial Logit via statsmodels

(MLE)

Evaluation

Metrics

MSE, MAE, Bias, and 95%

Confidence Interval Coverage Rate

3.3 Experimental Results and Analysis

The fusion model combines NN with multiple Logit

frameworks, possessing both nonlinear modeling

capabilities and parameter interpretability. The

experimental results show that this model performs

excellently in terms of parameter estimation

accuracy, error control and statistical properties. The

MSE is approximately 0.010, and the MAE is about

0.08. The 95% confidence interval coverage rate

remained stable above 0.95, demonstrating good

reliability. Compared with the pure NN model, the

fusion model can capture nonlinear structures more

effectively while retaining the explanatory power of

parameter behaviors, and is suitable for modeling

complex travel choice behaviors. The comparison

results of model performance are detailed in Table 4,

and the parameter estimation performance is shown

in Figures 3, Figure 4.

Table 4: Comparison of Model Performance in Monte Carlo Experiments.

Model Avg. MSE

Avg.

MAE

Avg.

Bias

Mean Coverage

Rate

Interpretability

Nonlinear

Modeling

Hybrid Model

(Ours)

≈ 0.0100 ≈ 0.079

< 0.01

≥ 0.95

Moderate–

High

Strong

Neural Network

Only

0.0100 ±

0.0003

0.0798 < 0.01

≈0.95

Poor Strong

Multinomial Logit 0.0121 0.0868 < 0.02 ≈ 0.95 Strong Weak

Figure 3: Distribution of Estimated Parameters. (Picture credit: Original)

A Monte Carlo Study of Integrating Discrete Choice Models and Neural Networks in Transportation Decision-Making

525

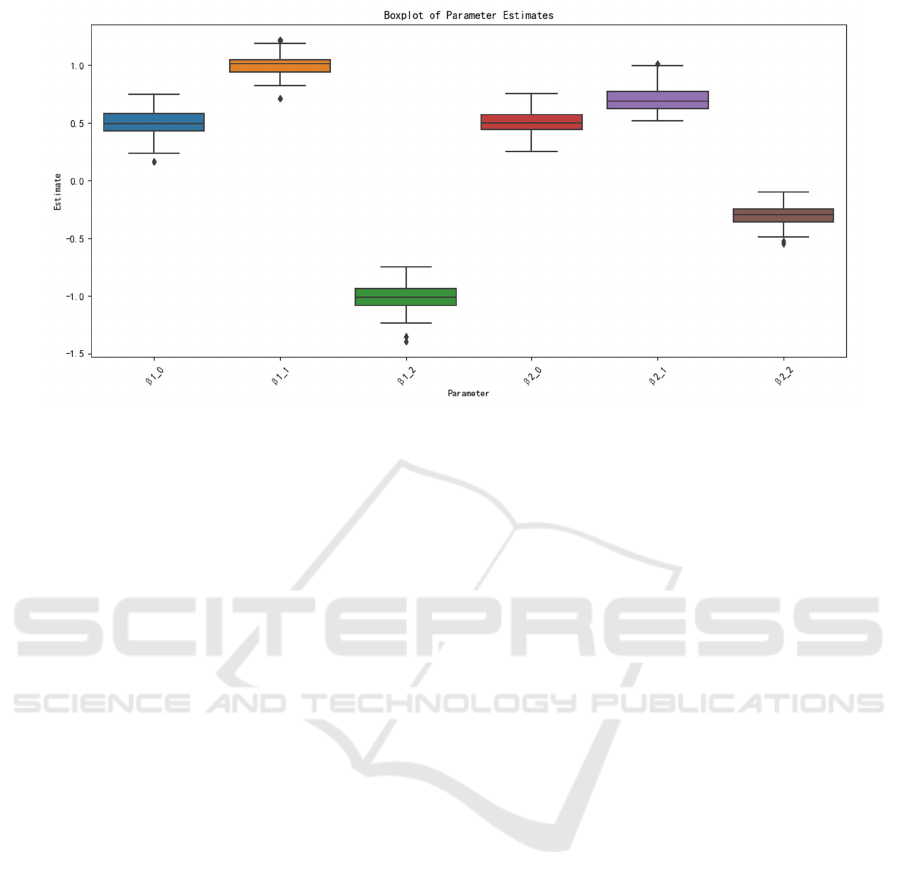
Figure 4: Boxplots of Estimated Parameter. (Picture credit: Original).

4 CONCLUSIONS

According to the Monte Carlo simulation experiment

results of this paper, the proposed hybrid discrete

selection model integrating the attention mechanism

neural network performs excellently in terms of

parameter estimation accuracy, stability and

confidence interval coverage. Compared with the

traditional MNL model, this model significantly

enhances its ability to describe nonlinear utility

structures and individual differences while

maintaining strong interpretability. In the experiment,

the estimation deviations of each parameter were

generally less than 0.01. Both MSE and MAE were

lower than those of the benchmark model, and the

coverage rate of the 95% confidence interval

generally reached or exceeded 0.95, indicating that

the model has good statistical properties and practical

application potential. In conclusion, this method

provides an effective tool for traffic behavior

modeling, especially suitable for the analysis of travel

choices in complex decision-making scenarios.

REFERENCES

Bhat, C. R. (2003). Simulation estimation of mixed discrete

choice models using randomized and scrambled Halton

sequences. Transportation Research Part B:

Methodological, 37(9), 837–855.

Bourguignon, F., Fournier, M., & Gurgand, M. (2007).

Selection bias corrections based on the multinomial

logit model: Monte Carlo comparisons. Journal of

Economic Surveys, 21(1), 174–205.

Hausman, J., & McFadden, D. (1984). Specification tests

for the multinomial logit model. Econometrica: Journal

of the Econometric Society, 1219–1240.

Kashifi, M. T., Jamal, A., Kashefi, M. S., Almoshaogeh, M.,

& Rahman, S. M. (2022). Predicting the travel mode

choice with interpretable machine learning techniques:

A comparative study. Travel Behaviour and Society, 29,

279–296.

Keane, M. P., & Wolpin, K. I. (1994). The solution and

estimation of discrete choice dynamic programming

models by simulation and interpolation: Monte Carlo

evidence. The Review of Economics and Statistics,

648–672.

Krishnapuram, B., Carin, L., Figueiredo, M. A., &

Hartemink, A. J. (2005). Sparse multinomial logistic

regression: Fast algorithms and generalization bounds.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 27(6), 957–968.

Li, J., Bioucas-Dias, J. M., & Plaza, A. (2010).

Semisupervised hyperspectral image segmentation

using multinomial logistic regression with active

learning. IEEE Transactions on Geoscience and

Remote Sensing, 48(11), 4085–4098.

Omrani, H. (2015). Predicting travel mode of individuals

by machine learning. Transportation Research Procedia,

10, 840–849.

Wang, F., & Ross, C. L. (2018). Machine learning travel

mode choices: Comparing the performance of an

extreme gradient boosting model with a multinomial

logit model. Transportation Research Record, 2672(47),

35–45.

Wong, M., & Farooq, B. (2021). ResLogit: A residual

neural network logit model for data-driven choice

modelling. Transportation Research Part C: Emerging

Technologies, 126, 103050.

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

526