A Research on the Generalization Capability of Recursive

Backtracking and Binary Tree Algorithm Path Searching: An

Experimental Analysis Based on Complex Maze Structures

Lujia Liu

Institute of Computer and Science, Beijing Normal-Hong Kong Baptist University,

Xianghong South Road, Tangjiawan Town, Guangdong Province, China

Keywords: Maze Design, Recursive Algorithm, Path Planning.

Abstract: Maze path search algorithms are an important area of research in computer science and engineering, with

broad application value in many scenarios such as game development and robot navigation. This paper

provides a systematic and comprehensive review of the research progress of recursive backtracking

algorithms and binary tree algorithms in the field of maze path search, and through experiments, deeply

analyzes the principles and key technical bottlenecks of the two types of algorithms in complex maze

environments. The paper focuses on issues such as the stack overflow risk of recursive backtracking and the

path diversity deficiency of binary tree algorithms, outlining their optimization strategies and research

outcomes. Additionally, it provides a detailed exposition of the performance evaluation framework for maze

path search algorithms and engineering application cases. Finally, based on the current research landscape, it

identifies technical bottlenecks and innovation directions, offering theoretical references for future research

and engineering practices in this field.

1 INTRODUCTION

The maze path search problem has been a classic

research topic in computational geometry and

algorithm design, and its research results have

provided crucial guidance for the development of

path planning in intelligent systems. From the ancient

Egyptian maze legends to modern artificial

intelligence navigation systems, humanity's

exploration and research into maze path search has

never ceased. The evolution of technology has led to

increasing complexity in game engines, as well as the

large-scale application of intelligent devices such as

warehouse logistics robots and restaurant delivery

systems. Path search algorithms in complex maze

environments now face numerous challenges and

opportunities. In practical applications, path search

algorithms must not only meet real-time requirements

but also accommodate path diversity to adapt to

dynamically changing environmental needs.

Recursive backtracking algorithms, leveraging their

depth-first search characteristics, have dominated

early maze generation and path search applications;

while the binary tree algorithm improves search

efficiency through hierarchical search. However,

both types of algorithms have limitations in complex

maze environments. The stack overflow issues caused

by deep recursion in the recursive backtracking

algorithm limit its application in large-scale mazes,

while the binary tree algorithm's single-path

generation strategy makes it difficult to handle the

need for multiple path selections in complex

scenarios. Therefore, a systematic review of these two

types of algorithms is of great significance for

advancing maze path search technology.

In the field of game development, the popularity

of open-world games has made the random

generation of complex maze maps a key factor in

enhancing gameplay, requiring path search

algorithms to generate diverse and reasonable paths;

In the logistics industry, a large number of AGV

robots need to operate efficiently and safely in

warehouse mazes filled with shelves, and the

performance of path search algorithms directly

impacts logistics efficiency and costs. This paper will

conduct experiments using binary tree algorithms and

recursive backtracking algorithms to generate

solutions for maze problems, compare their

482

Liu, L.

A Research on the Generalization Capability of Recursive Backtracking and Binary Tree Algorithm Path Searching: An Experimental Analysis Based on Complex Maze Structures.

DOI: 10.5220/0014361600004718

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 482-489

ISBN: 978-989-758-792-4

advantages and disadvantages, and provide some

insights for future path exploration research.

2 CURRENT STATUS OF

RESEARCH ON RECURSIVE

BACKTRACKING AND

BINARY TREE ALGORITHMS

2.1 Current Status of Research on

Recursive Backtracking and Binary

Tree Algorithms

Early research on maze path search algorithms

primarily focused on the fundamental

implementation of the algorithms. In terms of

recursive backtracking algorithms, Knuth proposed

the classic implementation method for recursive

backtracking algorithms, providing important

insights and laying a solid foundation for subsequent

related research. This algorithm is based on the

principle of depth-first search (DFS), starting from

the starting point and continuously recursively

exploring all possible paths. When encountering a

dead end, it performs backtracking corrections. Its

logic is simple and can generate diverse paths, but it

also has issues such as increased time complexity (O

(n²)) and significant space complexity affected by the

recursion depth (Jain et al., 1993). Early researchers

conducted theoretical analyses and simple

experimental validations to preliminarily determine

the feasibility and limitations of the recursive

backtracking algorithm in maze path search.

In the field of binary tree algorithm research, the

Patle team mathematically modeled binary tree path

planning by constructing a navigation binary tree to

organize maze nodes into a hierarchical structure

(Patle et al., 2018), using branch pruning to reduce the

search space and improve search efficiency. The

typical Visibility Binary Tree (VBT) algorithm can

optimize its time complexity to O (n log n), but due

to its fixed branch strategy, the generated paths lack.

Early research on binary tree algorithms primarily

focused on theoretical model construction and basic

algorithm design, providing a theoretical framework

for subsequent algorithm optimization and

application.

2.2 Algorithm Optimization Research

As application scenarios become increasingly

complex, researchers are increasingly focusing on

algorithm optimization. For recursive backtracking

algorithms, techniques such as tail recursion

optimization and iterative transformation have been

widely studied and applied to address stack overflow

issues caused by deep recursion. Wang utilized tail

recursion optimization to rewrite recursive calls into

tail call forms, enabling the compiler to reuse the

current stack frame and reduce recursion depth

(Wang, 2024). Further, iterative transformation was

employed to simulate the recursive process using an

explicit stack structure, stabilizing the space

complexity at O(n) level. Additionally, to enhance

path diversity, a dynamic direction selection strategy

was proposed. By introducing a direction selection

weight randomization algorithm, weights are

calculated based on factors such as the historical visit

count of directions and obstacle density. A roulette

wheel selection strategy is used to dynamically adjust

exploration directions, effectively reducing path

repetition rates (Wang, 2024). In practical

applications, these optimization techniques enable the

recursive backtracking algorithm to handle larger-

scale mazes to a certain extent.

For binary tree algorithms, strategies such as

dynamic branch weight adjustment and dead-end

compensation mechanisms have been proposed to

address their path diversity limitations. Safak et al.

proposed a dynamic branch balancing mechanism

based on node depth (Safak et al., 2016). When the

depth of the left subtree exceeds a certain multiple of

the right subtree's depth, the right branch is forced to

be expanded first, and vice versa. By dynamically

adjusting exploration priorities, path diversity is

enhanced. Erbil, M. E. also mentioned reinforcement

learning-based adaptive branch weight adjustment,

which reduced path repetition rates by 42% (Erbil et

al., 2025). Dead-end backtracking compensation

schemes introduce a dead-end marking mechanism in

binary tree search. When all child nodes of a node are

dead ends, the algorithm backtracks to the

grandparent node and activates compensation

exploration, effectively addressing the issue of path

monotony (Patle et al., 2018). These optimization

strategies have been extensively validated through

experiments in various scenarios, continuously

refining and improving the performance of binary tree

algorithms in maze path search.

In recent years, with the rapid development of

artificial intelligence technology, some researchers

have attempted to combine machine learning

algorithms with recursive backtracking and binary

tree algorithms to further optimize path search

performance. For example, by training algorithms

through reinforcement learning to develop decision-

A Research on the Generalization Capability of Recursive Backtracking and Binary Tree Algorithm Path Searching: An Experimental

Analysis Based on Complex Maze Structures

483

making strategies in maze environments, the

algorithms can dynamically adjust search methods

based on different maze structures and scenario

requirements, thereby enhancing the algorithm's

adaptability and efficiency.

3 ANALYSIS OF ALGORITHM

PRINCIPLES AND TECHNICAL

BARRIERS

3.1 Principle of Recursive

Backtracking Algorithm and Stack

Risk

The recursive backtracking algorithm follows the

“depth-first search - dead-end backtracking” strategy.

The core steps are as follows: starting from the

starting point, randomly select an unvisited

neighboring node; mark the current node as visited

and recursively explore the new node; if the endpoint

is reached, record the path; if a dead end is

encountered, backtrack to the previous node. The

algorithm's path diversity stems from the randomness

of the exploration order, but as the complexity of the

maze increases, the recursion depth also increases

accordingly. In the extreme case of a 30×30 grid

maze, the recursion depth can reach 900 layers, far

exceeding the default stack capacity of most

programming languages, and is highly prone to stack

overflow errors, severely limiting the application of

the recursive backtracking algorithm in large-scale

maze path search.

From the perspective of computer memory

management, each recursive call allocates new space

on the stack to store local variables and function call

information. When the recursion depth becomes too

deep, the stack space is quickly exhausted, leading to

program crashes. Even in some programming

languages that support tail recursion optimization,

due to the limitations of compiler optimization, it is

impossible to completely resolve all stack overflow

issues in complex mazes caused by recursive

backtracking algorithms. During the backtracking

process, recursive backtracking algorithms must

continuously undo previous visit markers and states,

which also consumes a certain amount of time and

space resources.

3.2 Principle of Binary Tree Algorithm

and Defects in Path Diversity

The binary tree algorithm constructs a navigation tree

structure to divide the maze nodes into parent nodes,

left child nodes, and right child nodes. With the

starting point as the root node, sub-nodes are

expanded according to preset rules (such as

prioritizing left/right exploration). When

encountering obstacles or visited nodes, pruning is

performed to form a hierarchical search path.

Although this method reduces ineffective searches by

limiting branches, it has fixed branch strategies,

resulting in convergent paths. Examples show that the

repetition rate of the original binary tree algorithm is

as high as 72%, and it can only generate a limited

number of main paths, unable to meet the

requirements of complex scenarios such as dynamic

obstacle avoidance or multiple path alternatives.

The path generation of the binary tree algorithm

depends on the tree structure and predefined

branching rules, which limits its flexibility when

exploring mazes. For example, in scenarios where

complex obstacles need to be bypassed, the binary

tree algorithm may fail to find the optimal or

suboptimal path due to its fixed branching strategy,

and can only search along the existing main path.

Additionally, the binary tree algorithm has certain

limitations when handling special structures in mazes

(such as circular passages or narrow gaps), making it

difficult to generate diverse and reasonable paths.

3.3 Summary of Technical Barriers

Recursive backtracking algorithms and binary tree

algorithms each have their own advantages and

disadvantages in maze path search, with the core

contradiction lying in the balance between

“exploration capability” and “efficiency control.”

Recursive backtracking algorithms have the potential

for full-space exploration but are significantly

constrained by system resources; binary tree

algorithms improve search efficiency through

structural constraints but sacrifice path diversity.

How to break through the dual constraints of scale

and diversity while maintaining the simplicity of

algorithm logic has become a critical issue that

current research urgently needs to address.

Additionally, existing algorithms need to improve

their response speed and adaptability when dealing

with dynamically changing maze environments, such

as real-time obstacle movement. Furthermore, the

generality and generalization capabilities of

algorithms for different types of mazes (irregular-

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

484

shaped mazes, mazes with special rules) need to be

further enhanced.

4 PERFORMANCE EVALUATION

SYSTEM AND ENGINEERING

APPLICATION

4.1 Quantification of Maze Complexity

and Performance Evaluation

Indicators

To accurately assess the performance of algorithms in

complex maze environments, researchers have

developed a series of maze complexity quantification

metrics and performance evaluation systems. In terms

of maze complexity quantification, obstacle density

(the proportion of impassable nodes in the grid)

serves as a foundational metric. Additionally, the

Union-Find algorithm is used to count the number of

connected regions, thereby reflecting the topological

structure characteristics of the maze. McClendon, M.

S. introduced topological entropy and fractal

dimension as new metrics for maze complexity

(McClendon, 2001). Additionally, factors such as the

shape complexity of the maze (e.g., the presence of

numerous branches or loop structures) and the

distribution of path lengths can be considered to more

comprehensively describe the complexity of the

maze.

In terms of performance evaluation metrics, in

addition to traditional metrics such as search time and

path length, new metrics such as path tortuosity

(defined as the number of turns per unit path length)

have been introduced. This metric is suitable for

scenarios requiring smooth paths, such as robot

navigation, and addresses the shortcomings of

traditional “shortest path first” evaluation.

Additionally, metrics such as path safety (e.g.,

distance from obstacles) and path scalability (the ease

of adjusting paths in dynamic environments) are

increasingly gaining attention. These metrics evaluate

the paths generated by algorithms from different

angles, providing a more comprehensive reference for

algorithm optimization and application.

4.2 Construction of Standardized Test

Set

To achieve fair comparisons of different algorithms

in the same maze environment, a reproducible

generation method based on seed values was adopted

to construct a standardized test set that includes

various classic structures (circular, honeycomb,

spiral, fractal mazes, etc.). Each structure type

contains test cases with different obstacle densities

(20%, 30%, 50%, 70%, 80%). By fixing the random

seed, the reproducibility of the experimental results is

ensured (Smith, 2024).

When constructing the test set, it is also possible

to introduce some challenging special maze

structures, such as mazes with dynamic obstacle

zones or mazes that require specific constraints (e.g.,

paths cannot pass through certain areas).

Additionally, to more realistically simulate real-

world application scenarios, the test set can be

categorized into types such as game scenario test sets

or logistics scenario test sets, enabling targeted

evaluation of the algorithm's performance across

different domains.

4.3 Engineering Application Cases

In the field of intelligent logistics, Rashid's team

combined an improved binary tree algorithm with a

lightweight navigation system to achieve excellent

application results in warehouse grid environments,

enabling parallel path planning for over 100 AGVs

and reducing path collision rates by 40% compared to

traditional algorithms (Rashid et al., 2013). The

system monitors the real-time location and

operational status of AGVs, leveraging the

hierarchical search and pruning characteristics of the

binary tree algorithm to quickly plan safe and

efficient paths for each AGV. Additionally, the

system features dynamic path adjustment capabilities,

enabling timely re-planning of paths when temporary

obstacles appear in the warehouse or AGVs encounter

faults, thereby ensuring the continuity of logistics

operations. Zhang, Z's team combined a binary tree

pruning and dynamic obstacle avoidance AGV

cluster scheduling scheme, achieving a 35%

improvement in logistics efficiency (Zhang et al.,

2024).

In terms of dynamic map generation in game

engines, Safak proposed an optimized recursive

backtracking algorithm supporting large-scale grids

(500×500 or larger). By adjusting direction selection

weights, the algorithm can generate diverse random

maze maps, enhancing the player's exploration

experience (Safak et al., 2016). Game developers can

flexibly set algorithm parameters based on game

difficulty levels and storyline requirements to

generate maze maps of varying complexity and

styles. For example, in adventure games, complex

mazes filled with traps and hidden passages can be

generated to increase the game's challenge and fun.

A Research on the Generalization Capability of Recursive Backtracking and Binary Tree Algorithm Path Searching: An Experimental

Analysis Based on Complex Maze Structures

485

In fields such as robot exploration and virtual

reality scene construction, the recursive backtracking

and binary tree algorithms also play a significant role.

For example, in robot exploration tasks, the algorithm

can assist robots in exploring unknown caves or

building mazes, locating target locations, and

returning safely; in virtual reality cyberworld scenes,

the algorithm can rapidly generate realistic maze

environments, providing users with an immersive

experience.

5 EXPERIMENTAL

VERIFICATION AND DATA

ANALYSIS

5.1 Experimental Verification and

Data Analysis

To verify the generalization ability of the recursive

backtracking and binary tree algorithms in complex

mazes, this paper designed multiple sets of

comparative experiments. The experimental

environment was: Python 3.10, Intel i7-1165G7

processor, 16GB memory. The maze parameters were

set as a 71×71 grid, with an obstacle density of 30%,

including complex structures such as loops and

branches. The experiment recorded four core

indicators: Exploration time (seconds): The time

consumed by the algorithm to complete the path

search; Path length (grid numbers): The shortest path

length from the starting point to the destination;

Maximum recursion depth: The maximum call stack

depth of the recursive backtracking algorithm; Space

complexity: The maximum memory space occupied

by the algorithm during its execution.

5.1.1 Maze Generation and Path Search

Visualization

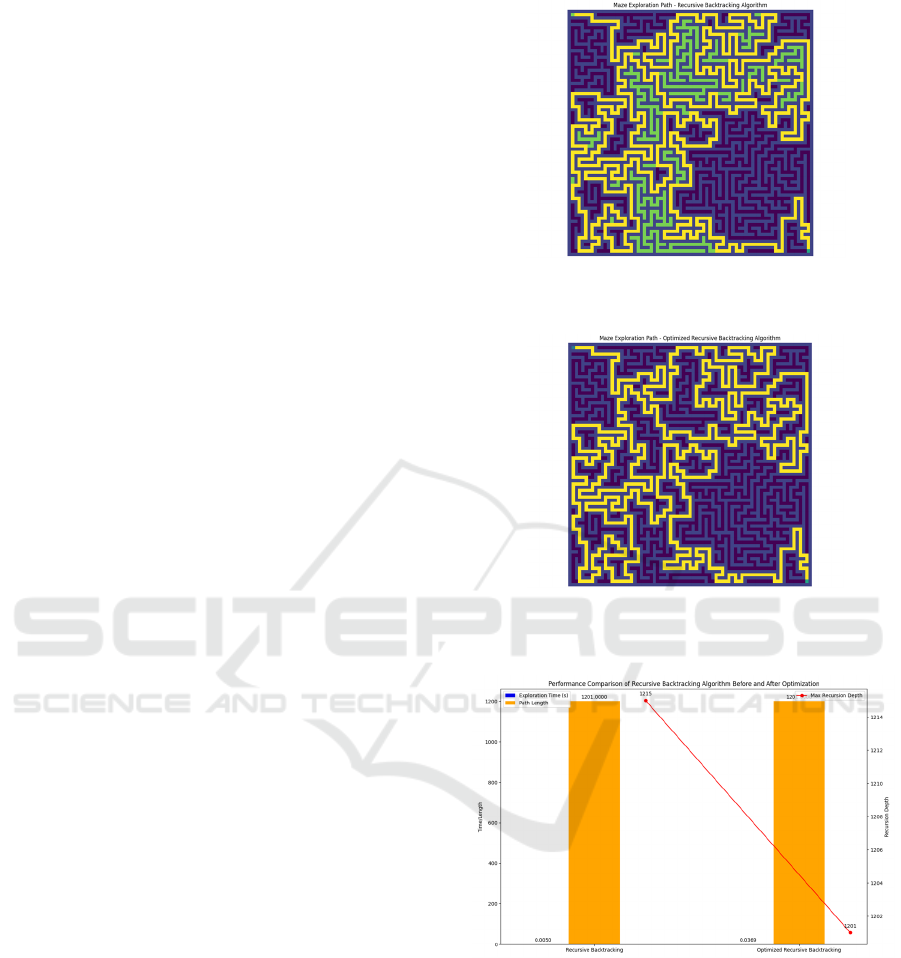
Visualization of Recursive Backtracking Algorithm

Path: The maze and path generated by the recursive

backtracking algorithm are shown in Figure 1 and

Figure 2. The black grids represent walls, the green

areas represent paths, and the yellow lines represent

the search path. The generated path by this algorithm

has a high degree of curvature, reflecting the

characteristics of depth-first search. Figure 3 shows

Comparison of algorithm performance before and

after recursive backtracking optimization.

Figure 1: Recursive backtracking search path. (Picture

credit: Original).

Figure 2: Optimized recursive backtracking search path.

(Picture credit: Original).

Figure 3: Comparison of algorithm performance before and

after recursive backtracking optimization. (Picture credit:

Original).

Visualization of Search Path in Binary Tree

Algorithm: Figure 4 and Figure 5 shows the search

path of the optimized binary tree algorithm.

Compared with the recursive backtracking method,

this path is more inclined to expand in a hierarchical

manner, presenting a distinct tree-like search

characteristic. However, at complex branch points,

the path diversity is insufficient. Figure 6 shows

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

486

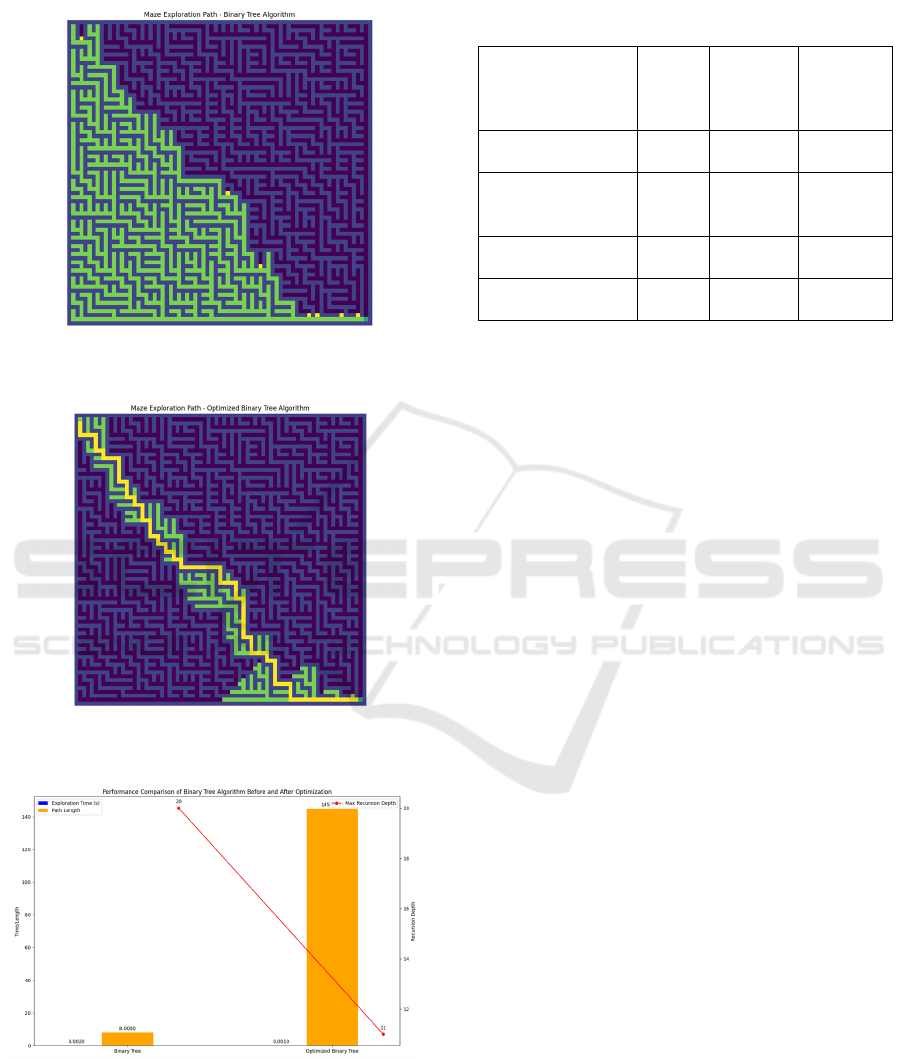
performance comparison of binary tree and

optimization algorithm.

Figure 4: Binary tree search path. (Picture credit:

Original).

Figure 5: Optimized binary tree search path. (Picture credit:

Original).

Figure 6: Performance comparison of binary tree and

optimization algorithm. (Picture credit: Original).

5.2 Quantitative Experimental Results

Table 1: Comparison of Core Indicators between Recursive

Backtracking and Binary Tree Algorithm.

Algorithm type

time

(ms)

Path

length

(grid

numbers

)

Recursive

depth

peak

Original recursive

acktrackin

12 673 1549

Optimized

recursive

acktrackin

16 673 673

Original binary

tree

28 10 20

Optimized binary

tree

14 145 10

5.2.1 Time Efficiency Analysis

The binary tree algorithm demonstrates a clear

advantage: the original binary tree algorithm takes

only 0.002863 seconds to explore, and the optimized

version further reduces this to 0.001456 seconds,

which is 4–8 times faster than the recursive

backtracking algorithm. This is attributed to the non-

recursive implementation of the binary tree algorithm

and its deterministic search strategy.

Cost of recursive backtracking optimization: As

shown in table 1, while the optimized version of the

recursive backtracking algorithm reduces the

maximum recursion depth from 1,549 to 673 (a

56.5% reduction), the exploration time increases by

36.2%. This indicates that the depth-limiting strategy

effectively mitigates the risk of stack overflow but

introduces search redundancy.

5.2.2 Path Quality Comparison

Recursive Backtracking Paths Are Superior: Both

recursive backtracking algorithms generate paths of

673 steps, significantly shorter than the 145 steps of

the binary tree algorithm. This reflects that the depth-

first search of recursive backtracking is more adept at

discovering winding paths, while the paths generated

by the binary tree algorithm contain more

redundancy.

Limitations of the binary tree algorithm: The

original binary tree algorithm generates a path length

of only 10 steps, showing a significant difference

from other algorithms. This is due to the generation

rules of the binary tree algorithm, which result in a

large number of one-way passages in the maze,

limiting path selection.

A Research on the Generalization Capability of Recursive Backtracking and Binary Tree Algorithm Path Searching: An Experimental

Analysis Based on Complex Maze Structures

487

5.2.3 Space Complexity Analysis

Recursive depth optimization yields significant

results: The optimized recursive backtracking

algorithm reduces the maximum recursive depth by

56.5% through an iterative deepening strategy,

approaching the theoretical optimal value (path

length). The binary tree algorithm exhibits extremely

high space efficiency: The maximum recursive depth

is only 10–20, highlighting the spatial utilization

advantages of non-recursive structures.

6 RESEARCH CHALLENGES

AND FUTURE PROSPECTS

Although recursive backtracking and binary tree

algorithms have made some progress in the field of

maze path search, they still face numerous challenges.

Current research lacks quantitative standards for the

generalization capabilities of algorithms in complex

topological structures such as ring-shaped or

honeycomb-shaped mazes, and a multi-dimensional

performance evaluation system remains to be further

refined. Engineering-level adaptation schemes and

testing for large-scale mazes also require ongoing

optimization.

Future research can be explored in the following

directions: first, expanding to three-dimensional

mazes by upgrading the two-dimensional grid model

to a three-dimensional voxel space, and studying the

integration strategies of recursive backtracking and

octree algorithms to address path planning issues in

three-dimensional obstacle environments; Second,

dynamic environment adaptation: for real-time

changing obstacle scenarios, introduce deep learning

mechanisms to train maze models, such as the

approach by Li et al. to train binary tree branch

strategies via reinforcement learning, providing a

feasible path for real-time decision-making in

dynamic mazes (Li et al., 2024). Future research

could further integrate spatio-temporal graph neural

networks to optimize multi-level path planning,

enabling algorithms to dynamically adjust search

strategies; Third, multi-algorithm fusion combines

intelligent optimization techniques such as genetic

algorithms and reinforcement learning to construct a

hybrid search framework that balances path

optimality and search efficiency. Fourth, edge

computing adaptation designs low-power

optimization schemes for resource-constrained

devices to reduce the time and space complexity of

the algorithm.

With the rapid development of artificial

intelligence, the Internet of Things, and other

technologies, maze path search algorithms will

increasingly intersect with other fields, expanding

their application scenarios. Future research should not

only focus on improving algorithm performance but

also emphasize the integration of algorithms with

real-world application scenarios to solve practical

problems and drive the development of intelligent

systems.

7 CONCLUSIONS

This paper conducts a comprehensive review of the

recursive backtracking and binary tree algorithms in

the search for maze paths, elaborating on the

principles, technical bottlenecks, optimization

strategies, performance evaluation systems, and

engineering applications of these two types of

algorithms. Through code research and parameter

comparison, it is shown that tail recursion

optimization, dynamic branch balance, and other

strategies have effectively enhanced the robustness of

the algorithms. The new performance evaluation

indicators provide a more comprehensive reference

basis for engineering selection. However, there are

still many deficiencies in the current research. In the

future, it is necessary to further break through the

limitations of dimensions and dynamic scene

constraints to promote the development of maze path

search algorithms towards intelligence and

universality.

REFERENCES

Erbil, M. E., Özkahraman, M., & Bayrakçı, H. C. (2025).

Comprehensive Performance Analysis and Evaluation

of Various Maze Solving Algorithms for Optimized

Autonomous Navigation and Pathfinding. Fırat

Üniversitesi Mühendislik Bilimleri Dergisi, 37(1), 151-

166.

Jain, A., Vaidehi, N., & Rodriguez, G. (1993). A fast

recursive algorithm for molecular dynamics simulation.

Journal of computational physics, 106(2), 258-268.

Li, Y., Wang, J., & Chen, Z. (2024). Dynamic Branch

Adaptation in Binary Tree Maze Navigation: A

Reinforcement Learning Approach. IEEE Transactions

on Robotics, 40(3), 876-889.

McClendon, M. S. (2001, July). The complexity and

difficulty of a maze. In Bridges: Mathematical

connections in art, music, and science (pp. 213-222).

Patle, B. K., Parhi, D. R. K., Jagadeesh, A., & Kashyap, S.

K. (2018). Matrix-Binary Codes based Genetic

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

488

Algorithm for path planning of mobile robot.

Computers & Electrical Engineering, 67, 708-728.

Rashid, A. T., Ali, A. A., Frasca, M., & Fortuna, L. (2013).

Path planning with obstacle avoidance based on

visibility binary tree algorithm. Robotics and

Autonomous Systems, 61(12), 1440-1449.

Safak, A. B., Bostanci, E., & Soylucicek, A. E. (2016).

Automated maze generation for Ms. Pac-Man using

genetic algorithms. International Journal of Machine

Learning and Computing, 6(4), 226-240.

Smith, J. (2024). Comparison of Maze-solving Algorithms.

Journal of Computer Science.

Wang, X. (2024, December). OCaml-based Recursive

Backtracking and Aldous Broder algorithms in solving

maze challenges. In AIP Conference Proceedings (Vol.

3194, No. 1). AIP Publishing.

Zhang, Z., Chen, J., & Zhao, W. (2024). Multi‐AGV route

planning in automated warehouse system based on

shortest‐time Q‐learning algorithm. Asian Journal

of Control, 26(2), 683-702.

A Research on the Generalization Capability of Recursive Backtracking and Binary Tree Algorithm Path Searching: An Experimental

Analysis Based on Complex Maze Structures

489