Comparative Implementation of Binary Tree and Recursive
Backtracking Maze Generation Algorithms in OCaml
Hengrui Zhang
Department of Computing, YanShan University, Qinhuangdao, China
Keywords: Maze Generation Algorithm, OCaml, Binary Tree Algorithm, Recursive Backtracking, Functional
Programming.
Abstract: Maze generation algorithm is a fundamental problem in computer science, which has a wide range of
applications in game design, path planning simulation, robot navigation and procedural content generation.
The choice of algorithm directly affects the structural properties of the maze, such as complexity, randomness
and solvability, which are crucial for specific application scenarios. This paper discusses the implementation
of maze generation algorithm based on binary tree and recursive backtracking using OCaml language. By
analyzing the design ideas of the two algorithms and their efficient implementation in OCaml, their
differences in performance, maze topology characteristics and application scenarios were compared. The
results show that the binary tree algorithm has fast generation speed and simple implementation, but the
complexity and randomness of the maze are low. The maze generated by the recursive backtracking algorithm
has high complexity and branching degree, but its implementation complexity is high. In addition, the
advantages of the two algorithms in different application scenarios are discussed, and the optimization
strategies are proposed. This study not only reflects the unique advantages of OCaml language in algorithm
design, but also provides an efficient and scalable solution for the practice of maze generation problem. It has
reference value for educational and industrial applications such as procedural generation.
1 INTRODUCTION
As a classic problem in the field of computational
geometry, the research value of maze generation is
not only reflected in the theoretical level, but also
shows strong practicability in the application fields
such as game development, robot navigation, virtual
reality and so on. With the development of computer
graphics and artificial intelligence technology, there
is an increasing demand for efficient and reliable
maze generation algorithms. Maze generation is the
process of creating a maze using a set of rules or
algorithms. Maze solving is the process of finding the
shortest path from a starting point to an endpoint in a
maze (Vijaya, Gopu, Vinayak, 2024). There are many
kinds of maze generation methods, among which the
algorithm based on binary tree and recursive
backtracking has attracted much attention because of
its high efficiency and the characteristics of the
generated maze. Recursive backtracking: A method
that can be used to solve chess problems, finding a
route in a maze, different artificial intelligence
problems is the backtracking method (Karova, Penev,
Kalcheva, 2016). This method examines all the
possible cases, usually starting from one specific
solution and seeking to broaden it with every step. If
it is determined that one of the following steps leads
to a dead end, the algorithm backtracks and attempts
a different step. This is accomplished through
recursion.
At the same time, functional programming
languages such as OCaml offer unique advantages for
the implementation of maze generation algorithms
due to their natural support for recursion and
immutable data structures. OCaml is a strongly typed,
multi-paradigm functional programming language.
Its powerful type system can accurately describe the
maze data structure and avoid common data
representation errors. Secondly, the pattern matching
feature simplifies the handling of various boundary
conditions in the algorithm. More importantly, the
optimization support for recursion in OCaml makes
the algorithm implementation both concise and
efficient. OCaml versions are generally better
maintainable and extensible than imperative
languages. The recursive splitting and recursive
246
Zhang, H.
Comparative Implementation of Binary Tree and Recursive Backtracking Maze Generation Algorithms in OCaml.
DOI: 10.5220/0014350200004718
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 246-251
ISBN: 978-989-758-792-4
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

backtracking algorithms for binary trees in the maze
generation problem can be succinctly and elegantly
expressed by OCaml. These two methods can
generate mazes with specific topological
characteristics. For example, the mazes generated by
the binary tree method usually contain long one-way
paths, Tree algorithm is faster and more efficient for
generating mazes with many cells, as it only considers
the edges that connect the current set of
nodes(Prasanth, Mukherjee, Vedasree Anusha,
2023). While the mazes generated by the recursive
backtracking algorithm have high complexity and
branching degree, Backtracking is a kind of
optimization search method. It searches forward
according to the optimization criteria, and when it
finds that the criteria are not met, it falls back and
selects again (Yuan, Yu, 2016).
This paper discusses how to use OCaml language
to implement maze generation algorithm based on
binary tree and recursive backtracking. First, the
paper will introduce the initialization of maze
generation and how it is represented in OCaml.
Secondly, the design ideas of the binary tree method
and the recursive backtracking algorithm are
analyzed in detail, and how to efficiently implement
these algorithms by using the recursion and pattern
matching characteristics of OCaml is shown. Finally,
the paper compares the performance of the two
methods and the topological properties of the
generated mazes, focusing on the following
problems: how to use pattern matching and recursion
modules of OCaml to elegantly model the maze
space; The performance differences and optimization
strategies of the two algorithms in the functional
paradigm; Discuss its application scenarios.
Through this study, the paper can gain insight into
the advantages of the ocaml language in algorithm
design, but also provide an efficient and scalable
solution for the practice of the maze generation
problem.
2 MANUSCRIPT PREPARATION
2.1 Related Configuration
Initialization: First, define an enumeration type
"direction" to represent the four directions of east,
south, west and north. Then define individual cells in
the maze. x and y are the coordinate positions of the
cells (immutable), which are used to precisely locate
the positions of the cells. walls is the list of walls
where the current cell exists (mutable, using the
mutable keyword), which can achieve dynamic
modification of the maze structure. is_entry marks
whether it is the entrance of the maze (mutable). The
is_exit flag indicates whether it is the exit of the maze
(variable). Finally, define the entire maze. "width" is
the width of the maze (the number of cells), "height"
is the height of the maze (the number of cells), and
"cells" is a two-dimensional array used to store all
cells, ensuring O(1) random access. The recursive
backtracking requires an extra Variable: visited, used
to indicate whether a cell has been visited. Each cell
is initialized to have four walls. All cells are not
entry/exit by default.
Related helper functions: A function checks
whether the specified cell has a wall in a certain
direction. A function removes walls in two directions
using the direction opposite to the collection
direction.
Remove wall: Remove the wall of the specified
direction and update the wall of the adjacent cell
synchronously.
Print: The entrance is marked "I" and the exit is
marked "O". Use "+" and "-" to indicate wall
intersections and horizontal walls. Use "|" for vertical
walls.
2.2 Binary Tree
Binary tree maze generation algorithm is a simple and
efficient maze generation method, which is especially
suitable for beginners to understand the basic
principle of maze generation. The maze generation
problem is essentially a spanning tree problem of a
graph, and Binary tree algorithm is commonly used
generation methods (Chen, 2020). The basic idea of
binary tree algorithm can be summarized as follows.
Each cell is randomly chosen to break either the east
or south wall, thus creating a maze path. Considering
the maze map as an undirected graph, the binary tree
algorithm can efficiently generate a connected and
loop-free maze path (Yuan, Yang, 2013). Figure 1
shows the flowchart of generating mazes using the
binary tree algorithm.
Specific steps:
First, iterate through each cell of the maze. Binary
tree traversal is the core part of the data structure
(Yang, Hu, Wang, 2023). After that, for each cell,
randomly choose to break the east wall (connected to
the cell on the right) or the south wall (connected to
the lower cell). Finally, the boundary cells
automatically adapt (the rightmost cell cannot break
the east wall, and the bottommost cell cannot break
the south wall).
Comparative Implementation of Binary Tree and Recursive Backtracking Maze Generation Algorithms in OCaml
247

Figure 1: Flowchart of the binary tree algorithm to generate
the maze. (Picture credit: Original).
2.3 Backtrack
The recursive backtracking algorithm is the classical
method to generate a perfect maze (that is, a maze
with one and only one path connecting any two
points), and adopts the depth-first search (DFS)
strategy. Backtracking is a systematic way to iterate
through all possible configurations to solve problems
like Sudoku, ensuring correctness by undoing invalid
choices (Anasune, Bhavsar, 2023).
Follow the following strategies: Random Walk:
Move in a randomly chosen direction from the
starting point. Break through walls: Break through
walls when moving to unvisited adjacent cells.
Recursively go deeper: Continue exploring deeper
from new locations. Backtracking mechanism: When
a dead end is encountered (all adjacent cells have
been visited), backtrack to the previous fork point
Gets all valid neighbors of the current cell (not out
of bounds), and returns a list in the format (x, y,
direction).
The depth-first search algorithm randomly selects
a path to break through the wall to form a maze
passage.
Initialize the random number generator, set the
entrance (top left) and exit (bottom right), make sure
the entrance and exit are open, and start the
generation from a random point. Figure 2 shows the
flowchart of the recursive backtracking algorithm for
generating mazes.
Figure 2: Flowchart of the recursive backtracking algorithm
to generate the maze. (Picture credit: Original).
3 RESULT
3.1 Binary Tree
Figure 3: Example of a binary tree generating a maze.
(Picture credit: Original).
EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence
248

Figure 3 shows an example of a binary tree for
generating mazes. There is a clear diagonal deviation
in the main direction. This is a direct consequence of
the binary tree algorithm, where each cell randomly
chooses to carve a channel right (east) or down
(south). This intrinsic randomness, coupled with the
grid structure, naturally leads to a preference for this
diagonal direction.
Straight corridors with few branches, binary tree
mazes are characterized by relatively long, straight
corridors. This is because the channels of each cell,
once carved, do not affect the generation of other
channels without creating many direct connections or
branches.
Compared to other maze generation algorithms
such as Prim or Kruskal, the binary tree maze has
fewer branching points. When branches occur, they
are usually short and quickly reconnected to the main
path.
All paths eventually merge into one main route,
and the binary tree maze is always connected,
meaning that there is a path from any cell to any other
cell.
While dead ends can still exist, their number is
usually smaller than some other maze types. The
nature of the algorithm encourages path joining rather
than early termination.
3.2 Backtrack
Figure 4: Example of recursive backtrack generating a maze.
(Picture credit: Original).
Figure 4 shows an example of recursively
backtracking to generate a maze. Recursive
backtracking produces more complex mazes: long,
winding main paths that tend to go deep into various
areas of the maze, forming complex networks of paths
instead of simple straight lines or direct paths, and
many shorter branching paths in addition to the main
path that are often unevenly distributed in length,
some very short and some relatively long.
When the recursive backtracking algorithm
generates the maze, it randomly chooses the direction
to explore, which leads to the formation of a large
number of branch paths in the maze. Due to the
randomness and depth-first characteristics of the
algorithm, there will be frequent dead ends in the
maze, and the branch path itself may continue to
branch, forming a multi-level branch structure.
Without direction preference, the algorithm has an
equal chance to explore in all directions, resulting in
a maze with a path that is relatively uniform in all
directions, a maze with roughly the same complexity
in all directions, and no direction significantly easier
or harder than any other.
3.3 Comparison of Results
Algorithm Concepts
The binary tree algorithm operates by linearly
iterating through each cell and randomly choosing to
remove either its east or south wall. This immediate,
localized decision-making results in relatively low
randomness, as each choice depends only on the
current cell. In contrast, the recursive backtracking
algorithm is based on depth-first search (DFS),
simulating an explorer who randomly selects
unvisited neighboring cells to carve paths into,
backtracking only when no options remain. This
approach exhibits high randomness, as each step
depends on the full history of prior choices and the
maze's evolving state.
Performance and Implementation
Both algorithms share O(n) time complexity (for
*n* cells), but differ in space use:
Binary tree: O(1) space—no auxiliary storage
needed beyond the maze grid. Walls are removed in a
single pass.
Recursive backtracking: O(n) space—requires a
stack (implicit via recursion or explicit) to track
visited cells and backtrack.
Ease of implementation:
Binary tree is simpler, requiring just nested loops
and random binary choices. Code is concise.
Comparative Implementation of Binary Tree and Recursive Backtracking Maze Generation Algorithms in OCaml
249

Recursive backtracking demands careful state
management (visited flags, stack operations),
doubling the code length.
4 DISCUSSION
4.1 Pros and Cons
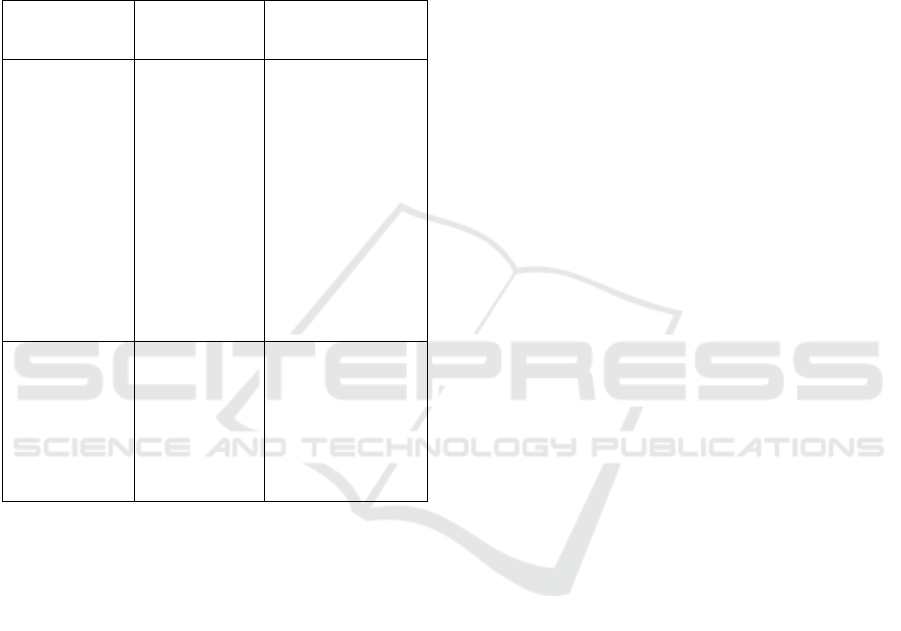
Table 1: pros and cons of both methods.
Algorithm Advantages Disadvantages
Recursive
backtracking
High quality
mazes
generated
Suitable for
exploratory
scenarios
High
teaching
value
Recursive calls
can cause stack
overflow
Slightly slower
generation
Has high
implementation
complexity
Binary tree
Extremely
fast
generation
Simple to
implement
Maze quality is
low
Deviated
Table 1 shows the advantages and disadvantages of
two methods
4.2 Applicable Scenarios
Recursive backtracking (dfs based) - Suitable for
complex scenarios
It can be applied to complex game mazes because
the natural twists, dead-ends, and branching paths of
its algorithms create attractive exploration
challenges. For example: roguelikes (like NetHack),
dungeon crawlers or escape room games, the
complexity of mazes can enhance gameplay. Also
great for algorithm teaching and demonstration,
illustrating DFS, backtracking, and stack-based
traversals in computer science courses. Example:
Visualizing how recursion "explores" paths and
retreats in dead ends helps students grasp core
concepts.
There is path-planning algorithm testing, which
stresses complex layout algorithms (e.g., A*,
Dijkstra) to deal with loops and long detour times.
Example: validating robotic navigation systems or AI
agents in unpredictable environments.
Binary Tree - simplest and fastest
Simple puzzle games can be made, instantly
generating mazes, clear, straight paths, suitable for
casual or time-sensitive games. For example: mobile
puzzle games (minimalist in the style of Monument
Valley) or fast procedural levels in 2D platformer
games. Perfect for embedded systems or
microcontrollers due to no recursion or stack
overhead (O(1) space). Example: Generating mazes
on low-power devices (e.g., Arduino-powered
chamber props). It is useful for rapid prototyping
because developers can quickly iterate without
debugging recursive logic and focus on the core
mechanics first. For example: game jams or early
prototypes, maze structures are secondary to
playtests.
4.3 Optimization Strategy
Optimization strategy of binary tree algorithm:
The orientation weights can be dynamically
adjusted, such as adjusting the probability of
removing the east/south wall based on the distance
from the current position to the exit. In addition, the
east wall or south wall of the exit can be forcibly
removed: the exit may be surrounded by walls.
Optimized traversal is used to traverse the string to
calculate the depth and number of leaf nodes of the
binary tree, which significantly reduces the space and
time complexity (Zhang, Wu, Liang, 2023). The
decision for each cell is set to be independent, and the
partition blocks can be processed in parallel (note
boundary synchronization).
Optimization strategy of recursive backtracking
algorithm:
An iterative implementation with an explicit stack
is used to avoid recursion depth exceeding the stack
limit. The neighbors are chosen directly at random,
since the list. The random comparison of Sort is
inefficient. Bitmaps, such as int arrays, can be
introduced instead of accessed Boolean arrays to
reduce the memory footprint. Combined with
probabilistic algorithm, probabilistic backtracking
composite algorithm combines the randomness of
probabilistic algorithm and the systematization of
backtracking algorithm, which significantly improves
the solution efficiency (Xu, Zhang, Li, 2021).
EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence
250

5 CONCLUSIONS
In this study, the maze generation algorithm based on
binary tree and recursive backtracking is
implemented by OCaml language, and the
performance, maze characteristics and application
scenarios of the two algorithms are analyzed and
compared in depth. The results show that the binary
tree algorithm is especially suitable for rapid
prototyping and scenarios with low complexity
requirements due to its simple implementation and
efficient generation speed. The maze generated by the
recursive backtracking algorithm has higher
complexity and branching degree, which is suitable
for complex application scenarios that require high-
quality mazes, such as game development and
algorithm teaching.
In the process of implementation, the features of
OCaml language, such as recursion support, pattern
matching and immutable data structure, significantly
improve the expression ability of the algorithm and
the maintainability of the code. In addition, the
optimization strategies (such as dynamically
adjusting the direction weight, iterative
implementation instead of recursion, etc.) are
proposed to further improve the efficiency and
applicability of the algorithm.
Future research directions could include
combining other algorithms such as Prim or Kruskal
to generate more diverse mazes, or exploring
parallelization techniques to further improve the
generation efficiency. This study not only provides a
practical solution to the maze generation problem, but
also provides a valuable reference for the application
of functional programming in algorithm design.
REFERENCES
Anasune, A. & Bhavsar, S. (2023). Image based Sudoku
Solver using Applied Recursive Backtracking. 2023
2nd International Conference on Futuristic
Technologies (INCOFT), 1-5.
Chen, J. (2020). Maze Generation and Pathfinding Program
Based on Scratch3.0. Digital Technology and
Applications, 38(9), 96-98.
Karova, M., Penev, I. & Kalcheva, N. (2016). Comparative
analysis of algorithms to search for the shortest path in
a maze. 2016 IEEE International Black Sea Conference
on Communications and Networking (BlackSeaCom),
1-4.
Prasanth, N. N., Mukherjee, M. S. K., Anusha, K. O. V.,
Bhat A. A. (2023). Generating and Solving Mazes
Using Parallel Minimum Spanning Tree Algorithms.
2023 Second International Conference on Smart
Technologies for Smart Nation (SmartTechCon), 831-
836.
Vijaya, J., Gopu, A., Vinayak, K. V. S. G., Singh, T. J. &
Malhotra, K. (2024). Analysis of Maze Generation
Algorithms. 2024 5th International Conference on
Innovative Trends in Information Technology
(ICITIIT),1-6.
Xu, S. F., Zhang, L. C. & Li, P. (2021). A Probabilistic
Backtracking Composite Algorithm for Solving the N-
Queen Problem. Modern Computer, 27(27), 24-30.
Yang, Y. F., Hu, J. Y., Wang, Y. X., et al. (2023). Binary
Tree Through Teaching Design and Practice of
Calendar Calculation Method. Computer and
Information Technology, 31(3), 51-54.
Yuan, H. F., Yu, H. M. (2016). Improved Backtracking
Algorithm to Realize the N Queen Problem Solving.
Computer Programming Skills and Maintenance,
(12),15-16+34.
Yuan, K. Y., Yang, Y. (2013). Design and Implementation
of Random Spanning Tree Algorithm for Planar Maze
Maps. Science Consultation (Technology &
Management), (01), 138-139.
Zhang, J. E., Wu, F. Y., Liang, Y. L. et al. (2023). Use
Parentheses Representation to Study the Optimal
Binary Tree Algorithm. Journal of Wind Science and
Technology, (29), 100-103.
Comparative Implementation of Binary Tree and Recursive Backtracking Maze Generation Algorithms in OCaml
251