Research on Machine Learning Based Stock Price Prediction Model

Tianhao Xue

The School of Computer and Data Engineering, Ningbo Tech University, Ningbo, China

Keywords: Machine Learning, Stock Price Prediction, Financial Market.

Abstract: With the continuous development of the financial market, individual stock price prediction has become an

important research topic in the field of quantitative investment and financial modelling. As one of the world's

leading technology companies, Amazon's stock price fluctuation is highly sensitive to the macroeconomic

environment, industry structure changes, and the company's own operating conditions, showing significant

nonlinear and complex dynamic characteristics. In this paper, the historical stock price data of Amazon from

2000 to 2025 is taken as the research object, and Ridge Regression, Random Forest and Gradient Boosting

Regressor models are constructed for model training. The experimental results show that the Gradient

Boosting Regressor model outperforms the other two models in terms of trend fitting and error control,

showing good generalisation performance and practical potential. This study aims to deepen the understanding

of the dynamic characteristics of financial markets and provide empirical references for individual stock price

prediction.

1 INTRODUCTION

With the development of financial technology and the

wide application of artificial intelligence technology,

data-driven quantitative modelling tools are playing

an increasingly important role in the securities market.

Stock price forecasting, as a core issue in financial

market analysis, is not only a key basis for investment

decisions, but also valuable in risk management, asset

allocation and other areas. Traditional technical

analysis methods and time series models, such as

moving average (MA) and autoregressive sliding

average (ARMA), although effective under specific

conditions, are often inadequate in dealing with the

nonlinear volatility and long- and short-term

dependence characteristics of stock prices.

In the financial market, stock price prediction has

been a hot research issue. With the enhancement of

computing power and the convenience of data access,

data-driven forecasting methods have gradually

replaced traditional statistical modelling methods and

become one of the important research directions in

both academia and practice (Mehtab et al., 2020;

Mehtab & Sen, 2020). In recent years, machine

learning techniques have shown strong potential in

modelling nonlinear relationships and mining time-

series data features (Qi, 2024).

https://orcid.org/0009-0004-7320-9531

Among many machine learning methods, Ridge

Regression (RR) is widely used in financial

modelling due to its effective mitigation of the

covariance problem (Ngui, 2023). In addition,

Random Forest Regressor, an integrated learning-

based algorithm, is able to maintain robustness and

interpretability when dealing with high-dimensional

financial data (Zheng et al., 2024; Khaidem et al.,

2016). Gradient Boosting Regressor, on the other

hand, is often used to construct high-performance

predictive models due to its strong fitting ability and

effective correction of bias (Reddy & Kumar, 2022;

Moodi et al., 2023).

It has been shown that these methods outperform

traditional time series models in stock price

forecasting. For example, Mehtab et al. compared the

effectiveness of Random Forest and Deep Learning

methods in price prediction (Mehtab & Sen, 2020);

Reddy and Kumar demonstrated the advantage of

gradient boosting machines over Random Forest in

terms of prediction accuracy (Moodi et al., 2023); and

Qi et al. compared ridge regression with LSTM

models, highlighting the importance of regularisation

in linear models (Adam et al., 2024). Meanwhile,

researchers have also tried to combine multiple

models for integrated prediction to improve stability

and generalisation (Kumar, 2025).

Xue, T.

Research on Machine Learning Based Stock Price Prediction Model.

DOI: 10.5220/0014325100004718

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 209-215

ISBN: 978-989-758-792-4

209

In this study, the historical stock price data of

Amazon.com from 2000 to 2025 will be used to

assess the comprehensive performance of three

methods, namely ridge regression, random forest

regression and gradient boosted regression, in the

price prediction task through feature engineering and

model comparison. By comparing their performance

in terms of metrics such as Mean Square Error (MSE)

and Coefficient of Determination (R²), the aim is to

select the most suitable modelling solution for this

dataset and to provide a systematic analysis of their

predictive capabilities.

This study is not only of theoretical significance,

which helps to enrich the application scenarios of

machine learning methods in the financial field; but

also of practical value, which provides investors,

quantitative traders and financial institutions with a

feasible modelling solution and tool support.

2 DATA ANALYSIS AND

MODELLING METHODS

Amazon.com, Inc. is a multinational technology

company that operates in a variety of sectors

including e-commerce, cloud computing, artificial

intelligence, digital streaming and logistics. The

company operates multiple global online retail

platforms and offers a wide range of products and

services to consumers and business customers. Its

cloud computing arm, Amazon Web Services (AWS),

is one of the world's leading cloud service providers.

Amazon's stock is listed on the NASDAQ exchange

under the symbol AMZN.

2.1 Stock Data Overview and K-Chart

Analysis

In this paper, the historical stock trading data of

Amazon (Amazon, ticker symbol: AMZN) from

December 2022 to December 2024 are selected,

containing key indicators such as daily opening price,

closing price, high price, low price and volume. In

order to analyse the short-term stock price

fluctuations more visually, the K-plot for the period

from December 2023 to December 2024 (see Figure

1) is plotted in this paper to observe the price trend

and market sentiment during the period.

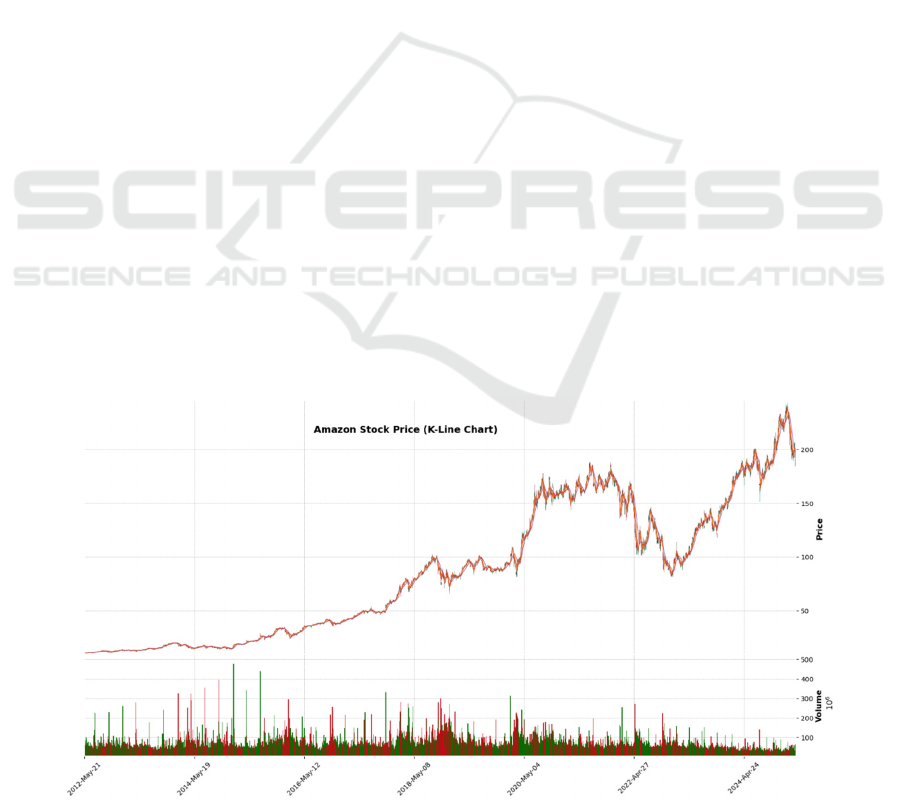
As can be seen in the Amazon stock K chart

(Figure 1), the stock price showed a clear upward

trend in early 2024. For example, the opening price

on 15 January 2024 was $118.33 and the closing price

was $121.45, forming a positive line and showing a

short-term rise. The stock price fluctuations are

relatively stable, indicating a positive market

sentiment. This volatility is valuable for short-term

trend prediction and feature extraction in machine

learning models.

However, the share price was more volatile on

certain dates, such as 7 February 2024, creating a long

shadow, suggesting that market sentiment was

unstable and affected by external factors.

Nonetheless, the share price ended up closing close to

the opening price, indicating a balanced market

sentiment.

Overall, the K-plot reflects the cyclical

fluctuations of the stock price, the changes in market

sentiment and the impact of volatility on the stock

price, and this information provides key features for

subsequent model training and helps to improve the

accuracy of short-term stock price forecasting.

Figure 1 Amazon stock K chart (Picture credit: Original)

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

210

2.2 Data Preprocessing

This paper first check for missing data and add the

missing values. Then the date fields are processed by

converting the date column date to datetime type and

extracting the year and month information in

preparation for the subsequent temporal

characterisation. In addition, duplicate values in the

data were identified and processed in this paper to

ensure the uniqueness and integrity of the data.

Descriptive statistical analyses were performed on the

numerical data to understand the distribution and

range of fluctuation of the data. Finally, columns that

were not relevant to the model predictions, including

date, year, month and adj_close (Adjusted Close

Price), were removed, and only variables that were

meaningful to the predictions were retained, such as

open price, close price and volume. These

preprocessing operations provide cleaned and

processed data for subsequent feature engineering

and model training.

2.3 Feature Engineering

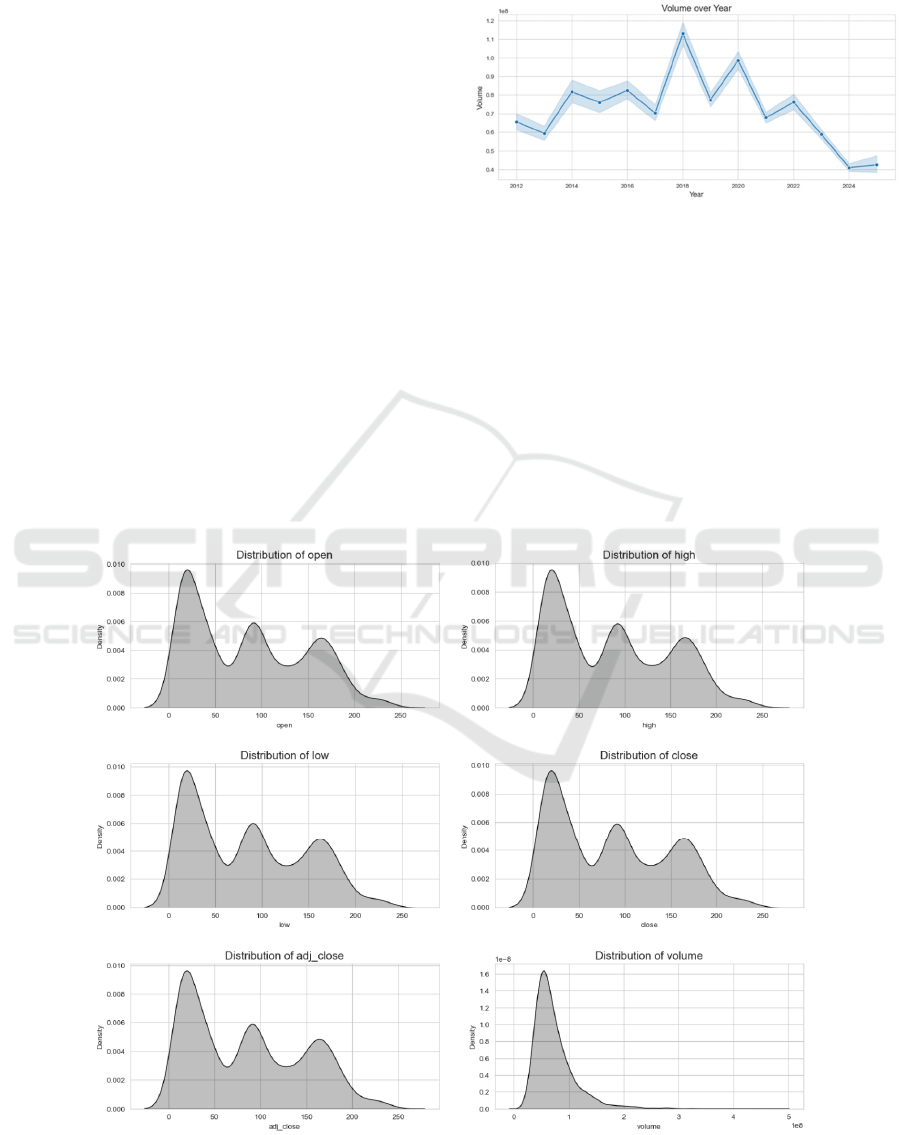
In this paper, by visualising the temporal features, as

in Fig. 2 the volume changes are plotted for different

years and months using sns. lineplot, which helps in

analysing the seasonal fluctuations in stock trading

and market trends.

Figure 2 Amazon stock annual trading volume trend chart

(Picture credit: Original)

In order to analyse stock price trends, as shown in

Figure 3 this paper plots the opening, closing, high

and low prices over time, thus visualising the trend of

price changes and providing a clear graphical

representation for understanding the historical

performance and volatility of stock prices.

To further understand the distribution of features,

as in Figure 4 this paper shows the distribution of

closing prices using violinplot (sns.violinplot), which

helps to identify distributional features and potential

outliers in the data.

Figure 3 Amazon stock characteristics over time (Picture credit: Original)

Research on Machine Learning Based Stock Price Prediction Model

211

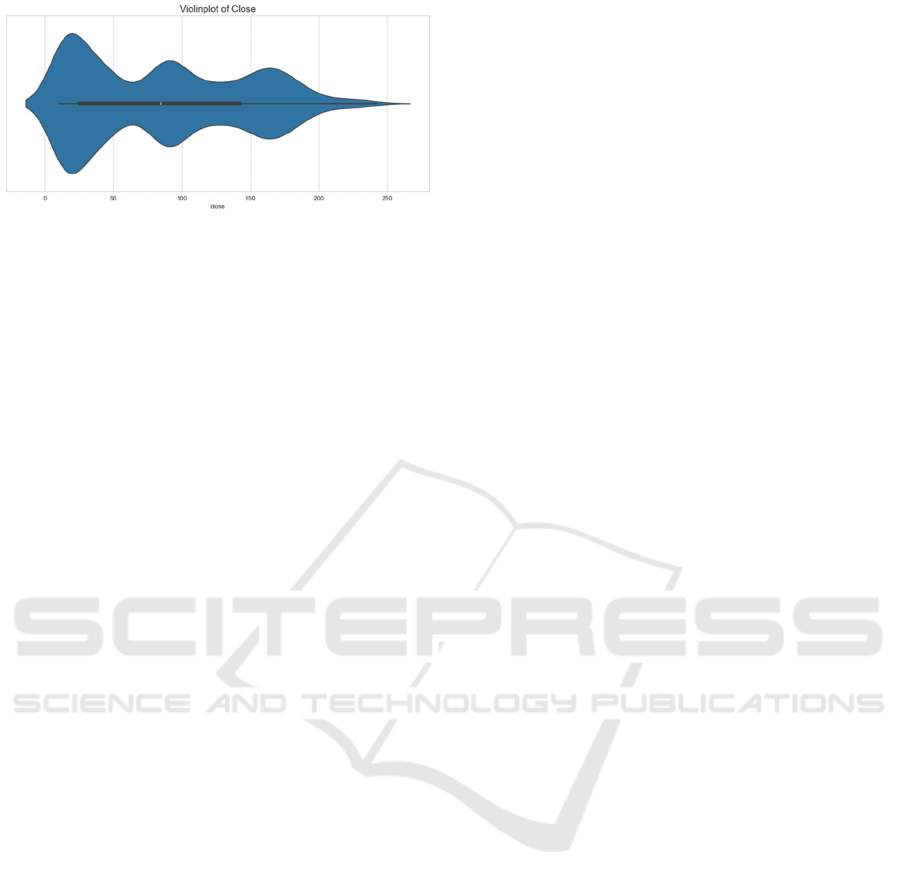
Figure 4 Amazon stock closing value violin chart (Picture

credit: Original)

Prior to model training, this paper uses

StandardScaler to normalise the feature data in the

training and test sets to ensure that the data meets the

requirements of the machine learning model and to

avoid model bias due to feature magnitude

differences.

2.4 Model Selection

2.4.1 Random Forest

Random forest is a regression model based on an

integrated learning method, which improves the

accuracy and stability of prediction by constructing

multiple decision trees and weighting the average of

their results. Compared with traditional regression

methods, Random Forest can effectively deal with

complex nonlinear relationships in high-dimensional

feature space and has strong noise immunity. In the

financial market, stock prices are affected by many

factors, and nonlinear relationships and complex

patterns are prevalent, so Random Forest can better

capture these complex market patterns. Although

Random Forest requires more computational

resources for model training and prediction, and

its‘black box’characteristic makes the model less

interpretable, its high prediction accuracy and good

generalisation ability make it an important model in

this study.

2.4.2 Ridge Regression

Ridge regression is an extension of linear regression

that reduces the complexity of the model and solves

the multicollinearity problem by introducing L2

regularisation. The core advantage of ridge regression

is that it avoids overfitting in the presence of highly

correlated features and maintains model stability. In

stock market data, the correlation between features is

strong, and using ridge regression can help alleviate

this problem and improve the predictive power of the

model. Compared with other regression methods,

ridge regression is computationally simple, efficient

in execution, and insensitive to small errors, which

allows it to maintain more reliable prediction results

in the face of complex market data. Therefore, ridge

regression was chosen as one of the benchmark

models for this study to compare with other more

sophisticated models.

2.4.3 Gradient Boosted Regression

Gradient boosted regression is an integrated learning

method that improves the prediction accuracy of a

model by progressively training multiple weak

learners (usually decision trees) and combining their

results to reduce errors in the previous round of

prediction. When dealing with the task of stock price

prediction, gradient boosted regression shows

superior nonlinear fitting and good prediction results,

especially when there are more complex patterns in

the dataset.GBR is able to adapt to trends and

fluctuations in financial market data and capture

subtle changes in the time series. Although the

training process of the method is time-consuming and

sensitive to the adjustment of hyperparameters, its

excellent predictive performance makes it an

important place in this study.

2.4.4 Basis for Model Selection

Three regression models, random forest regression,

ridge regression and gradient boosting regression,

were finally selected for this study with the following

considerations.

First is Adaptability and Performance. Random

Forest Regression and Gradient Boosted Regression

can effectively handle non-linear data and capture

complex market fluctuation patterns, while Ridge

Regression can deal with multicollinearity among

features and has high computational efficiency. The

three complement each other and can show different

advantages in different market situations.

Second is model complexity and computational

efficiency. Ridge regression is computationally

efficient due to its simpler model structure, and is able

to obtain more robust predictions in a short period of

time. In contrast, Random Forest Regression and

Gradient Boosting Regression have longer training

time due to their integrated learning characteristics,

but can provide higher prediction accuracy.

Third is interpretability and stability. Ridge

regression has an advantage in terms of model

interpretability, providing an intuitive analysis of

feature importance. While Random Forest Regression

and Gradient Boosted Regression have high

prediction accuracy, they are more difficult to

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

212

interpret within the model due to their integration

properties. Nevertheless, when faced with complex

stock market data, these models are able to provide

more accurate predictions and are therefore selected

as the main prediction models in this study.

3 MODEL TRAINING AND

ANALYSIS OF

EXPERIMENTAL RESULTS

3.1 Indicators for Model Evaluation

In order to comprehensively measure the

performance of each regression model in the task of

stock price forecasting, the following Mean Squared

Error (MSE) and Coefficient of Determination (R²)

are selected as the evaluation metrics in this

paper.MSE measures the squared average of the

difference between the predicted value and the actual

value, reflecting the overall prediction accuracy of the

model. n denotes the sample size, i.e., the total

number of data points included in the dataset. Yi

denotes the actual value of the ith sample, i.e., the real

observed data. 𝑦



denotes the predicted value of the ith

sample, i.e., the result predicted by the model based

on the input data. The summation symbols in the

formula are used to sum the errors for all samples,

while the error squared (𝑦



−𝑦



)



denotes the square

of the difference between the actual value and the

predicted value, and the squaring operation removes

the plus and minus signs of error and amplifies the

effects of larger errors. By calculating the MSE, can

quantify the model's prediction error; the smaller the

MSE value, the better the model's prediction.

𝑀𝑆𝐸 =

𝑛



(

𝑦



−𝑦





)







(

)

The coefficient of determination, R^2is a key

statistical indicator for assessing the predictive

accuracy of a model, with a value between 0 and 1.

The closer it is to 1, the better the model is at

explaining stock price movements. It is defined as:

𝑅



=1−

∑(

𝑦



−𝑦





)







∑(

𝑦



−𝑦

)







(

)

where n denotes the sample size, i.e., the total

number of stock price data points used for model

training and testing, 𝑦



is the actual stock price of the

ith sample, 𝑦



is the stock price of the ith sample

predicted by the model, while 𝑦is the average of the

actual stock prices of all the samples, 𝑅



is calculated

by comparing the

difference between the predicted and actual values

of the model (Residual Sum of Squares, RSS) as well

as the difference between the actual value and the

average value (Total Sum of Squares, TSS), whose

value is closer to 1 indicating that the model is more

capable of explaining the changes in stock prices.

3.2 Experimental Environment and

Development Platform

This experiment uses Windows 11 operating system

and Python 3.10 programming language, the

development work is mainly carried out in Jupyter

Notebook, the environment is configured and

managed by Anaconda, Table 1 shows the main

libraries and their functions used in this paper.

Table 1: shows the main libraries used in this paper and their functions.

Librar

Name Functional Descri

tion

andas Data loadin

and time series format

rocessin

num

Numerical Calculations and Arra

Mani

ulation

scikit-learn Provision of Ridge regression models, standardised tools and assessment indicators

matplotlib Plotting prediction comparisons, error visualisation charts

seaborn For o

timisin

chart aesthetics

3.3 Model Training and Tuning

During the training process, the model

hyperparameters were adjusted as necessary to

optimise the prediction performance. During the

implementation of the Ridge Regression model,

StandardScaler was used in this experiment to

preprocess the features to ensure the stability and

efficiency of model training. By setting the

regularisation parameter alpha to 1200.0 and

significantly enhancing the regularisation strength of

the model, this measure effectively reduces the risk of

overfitting. Thanks to the properties of the ridge

regression algorithm, the model training process not

only converges quickly, but also has a very high

computational efficiency, which makes it a reliable

Research on Machine Learning Based Stock Price Prediction Model

213

choice for dealing with datasets with multiple

covariate features.

When constructing the Random Forest model

(Random Forest), this experiment set the number of

trees (n_estimators) to 9 and the maximum depth

(max_depth) to 1, with a view to striking a balance

between model complexity and generalisation ability.

Initially, the default parameters were adopted as the

baseline model, and the model was carefully tuned

according to the actual performance of the test set.

Random Forest is known for its excellent nonlinear

fitting ability, which makes it particularly suitable for

capturing the volatility characteristics of non-

stationary time series data such as stock prices, and

thus performs well in data analysis.

In constructing the Gradient Boosting Regressor

(GBR) model, the parameter configurations of 0.01

for the base learning_rate and 100 for the number of

iterations (n_estimators) were chosen in this

experiment to strengthen the learning effect of the

model on the data. Compared with the random forest

regression model, gradient boosting regression

focuses more on the fitting of residuals in each

iteration, thus demonstrating its superiority in

generalisation ability. Despite its relatively long

training time, it is usually able to achieve higher

prediction accuracy.

3.4 Presentation and Comparison of

Experimental Results

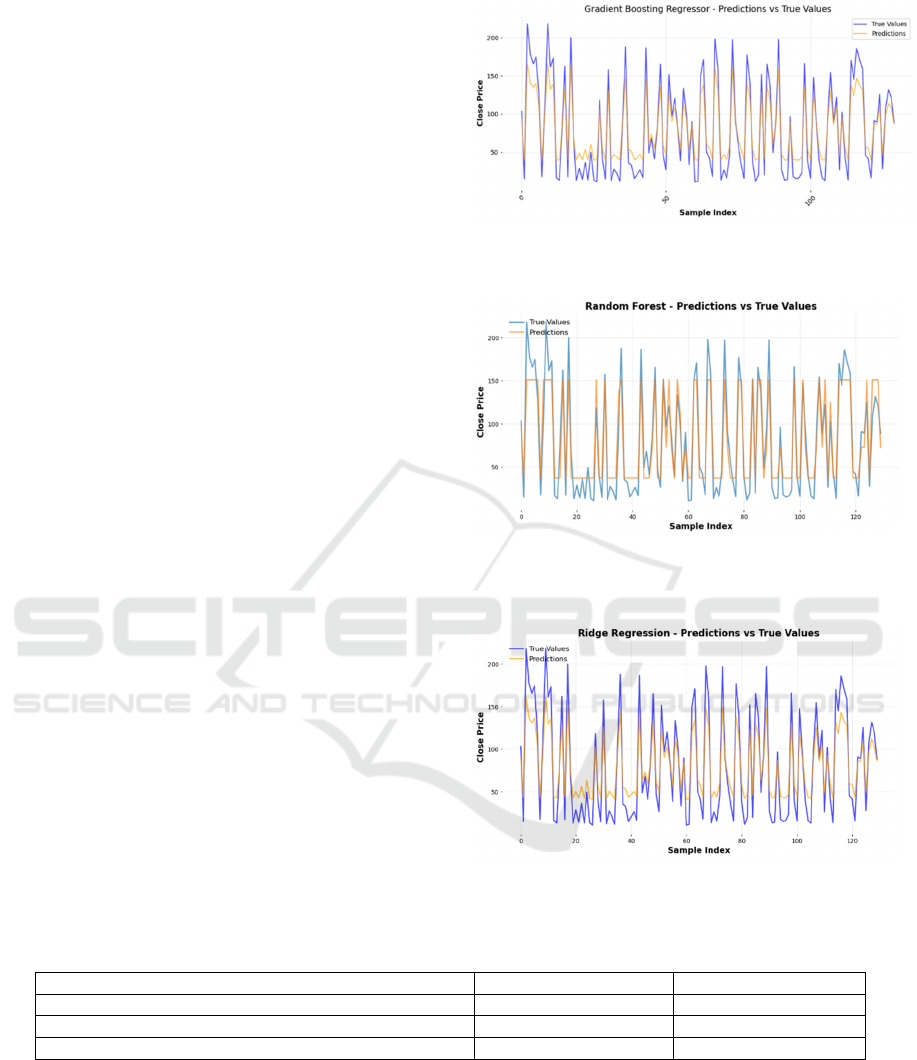
After the completion of the experiments, line plots of

the predicted value versus the actual stock price of

each model on the test set are plotted (Figure 5, Figure

6, Figure 7) to visually demonstrate the model's

fitting ability and the degree of trend capturing.

Figure 5: Gradient Boosting Regressor Predicted Values vs

True Values.

Figure 6: Comparison of predicted and true values of

Random Forest model.

Figure 7: Ridge regression model predictions vs true values.

Table 2: Comparison of models.

Model name MSE R²

Gradient Boosting Regresso

535.13 0.87

Random Forest 440.96 0.87

Rid

e Re

ression 435.06 0.82

Table 2 shows the experimental results of

different models. From the above experimental

results, it can be seen that the ridge regression model

performs stably within the smooth trend interval of

the data, but its prediction accuracy decreases when

facing large fluctuations in the data. The Random

Forest model, on the other hand, demonstrates the

ability to capture complex nonlinear features and is

particularly suitable for dealing with sudden ups and

downs in the data. The gradient boosting model, on

the other hand, performs the best among all the

models, as it not only achieves the highest R² value,

but also has the smallest integrated error, and is

therefore considered the optimal forecasting model.

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

214

Taken together, the gradient boosting regression

model satisfies the experimental criteria due to its

superior prediction accuracy and is finally

recommended as the main prediction model in this

paper.

4 CONCLUSIONS

Based on the historical stock price data of

Amazon.com from 2000 to 2025, this paper explores

the performance differences of three typical machine

learning regression models with different feature

dimensions and training strategies around the stock

price prediction task. The experimental results show

that ridge regression has a good fitting effect in the

smoother data interval, and the model is concise and

stable in training; the random forest model shows

some advantages in dealing with nonlinear

relationships and feature interactions, but has a high

parameter dependence and is prone to overfitting on

the training set; and the gradient boosting model

shows stronger generalisation ability and robustness

in capturing stock price trends and detailed

fluctuations, and is suitable for complex financial

forecasting environment. Through comparative

analysis, this study not only verifies the effectiveness

of integrated learning models in stock price

prediction, but also provides empirical references for

modelling practices in related fields.

Although this study has achieved some results,

there are still some limitations. Firstly, limited by the

data structure and feature selection, the model has a

limited ability to respond to unexpected events and

extreme market conditions; secondly, more

sophisticated deep learning models, such as LSTM or

Transformer architectures, were not introduced in the

study, and their potential for modelling time series

has not been fully explored. Future research can

further expand in the following aspects: introducing

heterogeneous data from multiple sources (e.g., news,

financial reports, macro indicators) to improve the

diversity and depth of features; applying deep

learning and hybrid modelling techniques to enhance

the model's ability to understand time series structure

and market sentiment; and further optimising the

model tuning strategy and validation method to

improve the practicability and popularity.

In summary, this study demonstrates the

promising application of machine learning in

financial time series forecasting, showing that data-

driven methods have strong modelling capabilities

and decision support value in complex market

environments.

REFERENCES

Adam, H. A., Raditiansyah, F., Imani, M. R., Fawwaz, M.

F., Julham, J., & Lubis, A. R. (2024). Comparison of

ARIMA and LSTM Models in Stock Price Forecasting:

A Case Study of GOTO. JK. Journal of Informatics and

Telecommunication Engineering, 8(1), 94–105.

Khaidem, L., Saha, S., & Dey, S. R. (2016). Predicting the

direction of stock market prices using random forest.

arXiv preprint arXiv:1605.00003.

Kumar, A. (2025). Developing a Stock Price Predictor:

Enhancing Investment Strategies with Machine

Learning. [Online]. Available:

https://medium.com/@amit.saptech/developing-a-

stock-price-predictor-enhancing-investment-strategies-

with-machine-learning-7bcb5aeb5a85

Mehtab, S., & Sen, J. (2020, November). Stock price

prediction using CNN and LSTM-based deep learning

models. In 2020 International Conference on Decision

Aid Sciences and Application (DASA) (pp. 447–453).

IEEE.

Mehtab, S., Sen, J., & Dutta, A. (2020, October). Stock

price prediction using machine learning and LSTM-

based deep learning models. In Symposium on Machine

Learning and Metaheuristics Algorithms, and

Applications (pp. 88–106). Singapore: Springer

Singapore.

Moodi, F., Jahangard-Rafsanjani, A., & Zarifzadeh, S.

(2023). Feature selection and regression methods for

stock price prediction using technical indicators. arXiv

preprint arXiv:2310.09903.

Ngui, S. W. (2023). How to Use Ridge Regression to

Predict a Stock Price. Medium. [Online]. Available:

https://swngui.medium.com/how-to-use-ridge-

regression-to-predict-a-stock-price-1b0099320ef4

Qi, Y. (2024). Research on Stock Price Prediction Based on

LSTM Model and Random Forest. Advances in

Economics, Management and Political Sciences, 86,

35–42.

Reddy, P. V., & Kumar, S. M. (2022, December). A novel

approach to improve accuracy in stock price prediction

using gradient boosting machines algorithm compared

with naive Bayes algorithm. In 2022 4th International

Conference on Advances in Computing,

Communication Control and Networking (ICAC3N)

(pp. 695–699). IEEE.

Zheng, J., Xin, D., Cheng, Q., Tian, M., & Yang, L. (2024).

The random forest model for analyzing and forecasting

the US stock market in the context of smart finance.

arXiv preprint arXiv:2402.17194.

Research on Machine Learning Based Stock Price Prediction Model

215