HABC Algorithm Optimization for Hybrid Flow Shop Scheduling

Under Blocking and Finite Buffer Constraints

Zhuoran Wang

Immersion Academy, 4010 Barranca Parkway Suite 252, Irvine, California, 92604, U.S.A.

Keywords: Hybrid Flow Shop Scheduling, Limited Buffers, Hybrid Artificial Bee Colony (HABC) Algorithm.

Abstract: This study focuses on the hybrid flow shop scheduling problem with limited buffers, a critical challenge for

improving manufacturing efficiency. An improved Hybrid Artificial Bee Colony algorithm (HABC) is

proposed, integrating WPFE initialization, Genetic Algorithm (GA) crossover-mutation operations, and

Variable Neighborhood Search (VNS). Validated using real production data from Sany Heavy Industry,

computational experiments demonstrate the superiority of HABC over conventional ABC and GA approaches.

Key findings include: HABC significantly reduces the makespan (e.g., a 1.61% reduction compared to GA)

and decreases blocking occurrences. The algorithm achieves faster convergence, reaching 95% of the optimal

value in approximately 4 seconds, with convergence times reduced by about 42% and 51% compared to ABC

and GA, respectively. Buffer capacity, particularly the zero-buffer scenario, exerts a profound impact on

scheduling efficiency. This research provides a practical scheduling solution for discrete manufacturing

enterprises, demonstrating HABC’s potential for optimizing real-world production scheduling. The work

contributes both theoretical and practical advancements to industrial scheduling optimization.

1 INTRODUCTION

As a core challenge in manufacturing system

optimization, the Hybrid Flow Shop Scheduling

Problem (HFSP) is prevalent in complex production

scenarios. Traditional research has predominantly

relied on the assumption of "unlimited buffer

capacity," neglecting practical issues such as

equipment blockage and logistical bottlenecks in real-

world production environments. The combination of

varying process cycle times and spatial constraints in

workshops leads to extended production cycles and

resource waste. As an NP-hard problem, exact

algorithms like branch-and-bound methods struggle

with real-time requirements due to high

computational complexity, making meta-heuristic

algorithms a critical technical pathway. The Artificial

Bee Colony (ABC) algorithm demonstrates

promising potential in limited-buffer scenarios due to

its parameter simplicity and strong global search

capabilities.

Existing research explores HFSP with limited

buffers from multiple perspectives: Yuan established

a multi-objective scheduling model using NSGA-

https://orcid.org/0009-0007-4036-8968

series algorithms, confirming the significant impact

of buffer capacity on completion time metrics (Yuan,

2021). Li et al. systematically analyzed the strengths

and weaknesses of various algorithms, highlighting

the research value of buffer constraints (Li et al.,

2024). Xie et al. proposed a Migrating Birds

Optimization algorithm with neighborhood search to

improve total flow time in blocked scenarios (Xie et

al., 2015). In algorithm enhancements, Hu et al.

designed an ant colony algorithm with optimized

encoding strategies (Hu et al., 2006). Mou et al.

combined a multi-population genetic algorithm to

enhance multi-objective optimization (Mou et al.,

2020). Luo et al. developed a discrete cuckoo

algorithm for improved parallel machine scheduling

(Luo et al., 2021). Qi and Zhao respectively enhanced

algorithmic stability through hybrid strategies

integrating particle swarm optimization with tabu

search (Qi and Zhao, 2012). Song et al. created a

three-level hierarchical ant colony algorithm for batch

scheduling (Song et al., 2021). Zhang et al. improved

ABC algorithm performance in limited-buffer

environments (Zhang et al., 2021).

162

Wang, Z.

HABC Algorithm Optimization for Hybrid Flow Shop Scheduling Under Blocking and Finite Buffer Constraints.

DOI: 10.5220/0014324200004718

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 162-168

ISBN: 978-989-758-792-4

Two critical gaps remain: First, the interaction

between buffer sizes and production rates across

processes remains understudied, making it difficult to

accurately predict equipment blockage occurrences

and dynamics. Second, traditional ABC algorithms

tend to fall into local optima when handling complex

production constraints, necessitating specialized

improvements in search strategies (Fan, 2012).

Based on real-world data from SANY Heavy

Industry's workshops, this study proposes an

enhanced ABC algorithm for hybrid flow shop

scheduling (HFSP) with equipment blockage and

limited buffers. The approach incorporates discrete

encoding for production sequences, integrates digital

simulators to accurately model workshop layouts and

output completion times, and combines genetic

algorithms with variable neighborhood search to

optimize efficiency. This research aims to address the

shortcomings of existing algorithms in complex

scenarios and provide practical scheduling

optimization solutions for industrial applications.

2 METHODS

2.1 Problem Description

For the hybrid flow shop scheduling problem with

blocking and restricted buffers, an improved Hybrid

Artificial Bee Colony (HABC) algorithm is proposed.

The core elements of the problem are formally

defined as follows.

2.1.1 Symbol Definition

Table 1 and 2 list core symbols for hybrid flow shop

scheduling, including workpiece sets, machine stages,

parallel machines, and time parameters, providing

formal definitions for mathematical modeling.

Table 1: Symbol definition.

mbol Descri

tion

J =



1,2,...,n



Set of workpieces,

containing 𝑛 workpieces

M =



1,2,...,m



Set of machine stages,

containing 𝑚 stages



Number of parallel

machines at stage 𝑘



Buffer capacity between

stage 𝑏 and stage

𝑏+1(b=1,2,...,m−1)

Table 2: Symbol Definitions for Process Operations and

Time Parameters.

Symbol Description



The 𝑗-th operation of workpiece i (j=

1,2,...,l



,where l



is the number of

operations for workpiece i)





Processing time of the j-th operation of

workpiece i at stage k





Start time of the j-th operation of

workpiece j at stage k





Completion time of the j-th operation of

workpiece i at stage k(C













)



(t)

Number of workpieces in the buffer

between stage b and b+1 at time t

(



(t) ≤ C



）

Makespan

=max

∈





Maximum completion time

2.1.2 Constraints

Table 3 specifies three key constraints: operation

sequence, machine exclusivity, and buffer capacity,

forming criteria for feasible scheduling solutions in

production logic.

Table 3: Constraints.

Constraint

Type

Description Formula

Operation

Sequence

Constraint

The operations of

workpiece 𝑖 must be

executed in stage

order.

()(



)

≥C



Machine

Exclusivity

Constraint

Any machine at

stage 𝑘 can process

only one workpiece at

a time.

∀i ≠

i′，C



≤



≤S





Buffer

Capacity

Constraint

The number of

workpieces in the

buffer between

stage 𝑏 and 𝑏+1 at

time 𝑡 must not exceed

its capacity.



(t)

≤C



2.1.3 Objective Functions

Table 4 defines the objective as minimizing

makespan, a classic indicator in hybrid flow shop

scheduling to quantify overall production efficiency.

HABC Algorithm Optimization for Hybrid Flow Shop Scheduling Under Blocking and Finite Buffer Constraints

163

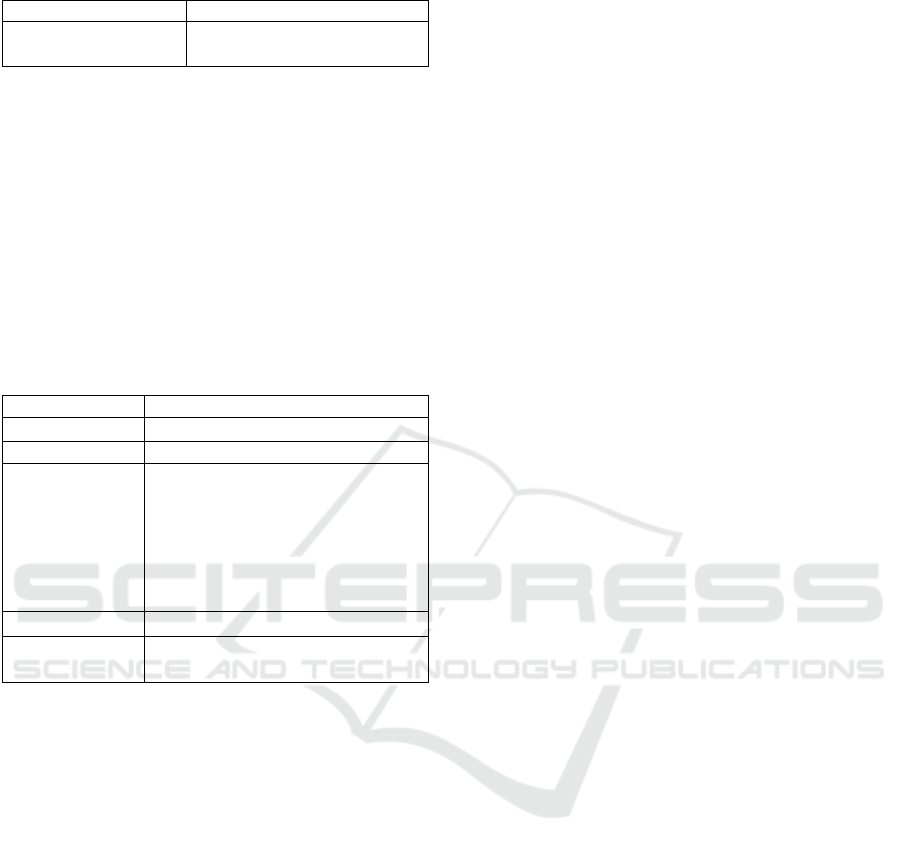
Table 4: Objective Function

Descri

tion Formula

Minimize the

makespan

min Makespan

= min



max

∈







2.2 Data Sources and Description

Table 5 provides parameters from SANY factory's

actual production data, including products, stages,

parallel machines, processing times, and buffers,

supporting algorithm validation in industrial

scenarios.

The data originates from real production cycle

records of the SANY factory, covering 5 product

categories (A, B, C, D, E) with processing times and

parallel machine configurations across 27 processes.

Table 5: List of Variables

mbol Value Ran

𝑛

𝑛=5×6=30

𝑚 𝑚=27

𝐾





























and 1 for the remaining stages

𝑝



500≤𝑝







≤2000

𝐶





=1，C



=6，C



=3，C







2.3 Methodology Introduction

2.3.1 Population Initialization and Encoding

The encoding scheme adopts a workpiece

permutation-based discrete encoding π=





,π



,...,π





. The initialization strategy generates

the initial population by using an improved NEH

heuristic, which enhances the quality of the initial

solution and reduces machine idle time and workpiece

blocking.

2.3.2 Hybrid Leading Bee Mechanism

The genetic algorithm (GA) is embedded in the

leading bee phase for parallel hybrid optimization:

For GA global search, tournament selection,

partially matched crossover (PMX), and

insertion/swap mutations are used to diversify

offspring solutions and expand the search space.

For RIS local search, random insertion (RIS -

Insert) or swap (RIS - Swap) is employed to

strengthen neighborhood exploration while balancing

global exploration and local exploitation.

2.3.3 Variable Neighborhood Search for

Local Intensification

The VNS algorithm based on insertion and exchange

neighborhoods is executed on high - quality solutions

to enhance local fine - search capability by alternately

exploring different neighborhood structures.

2.3.4 Multi-phase Collaborative

Optimization

In the scout bee phase, candidate solutions are

screened using tournament selection, new solutions

are generated via RIS operations, and superior

individuals are retained.

In the scout bee phase, 3 insertion mutations are

performed on solutions with no continuous

improvement to avoid local optima.

The digital simulator dynamically evaluates the

feasibility of solutions based on operation processing

times and buffer constraints, calculates the maximum

makespan, and ensures that scheduling plans comply

with blocking rules.

3 RESULTS AND DISCUSSION

3.1 Algorithm Performance

Comparison

Based on the real buffer configurations from Sany

Heavy Industry’s factory data (buffer C



with

capacity=1 between processes 2-3, buffer C



with

capacity=6 between processes 9-10, buffer C



with

capacity=3 between processes 23-24, buffer C



with capacity=5 between processes 24-25, buffer C



with capacity=5 between processes 25-26, and buffer



with capacity=5 between processes 26-27), the

performance of the improved Hybrid Artificial Bee

Colony algorithm (HABC) was compared with

traditional Artificial Bee Colony (ABC) and Genetic

Algorithm (GA). Table 6 presents the average results

from 50 independent runs, with core metrics

including makespan and blocking occurrences

(reflecting buffer constraint effects).

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

164

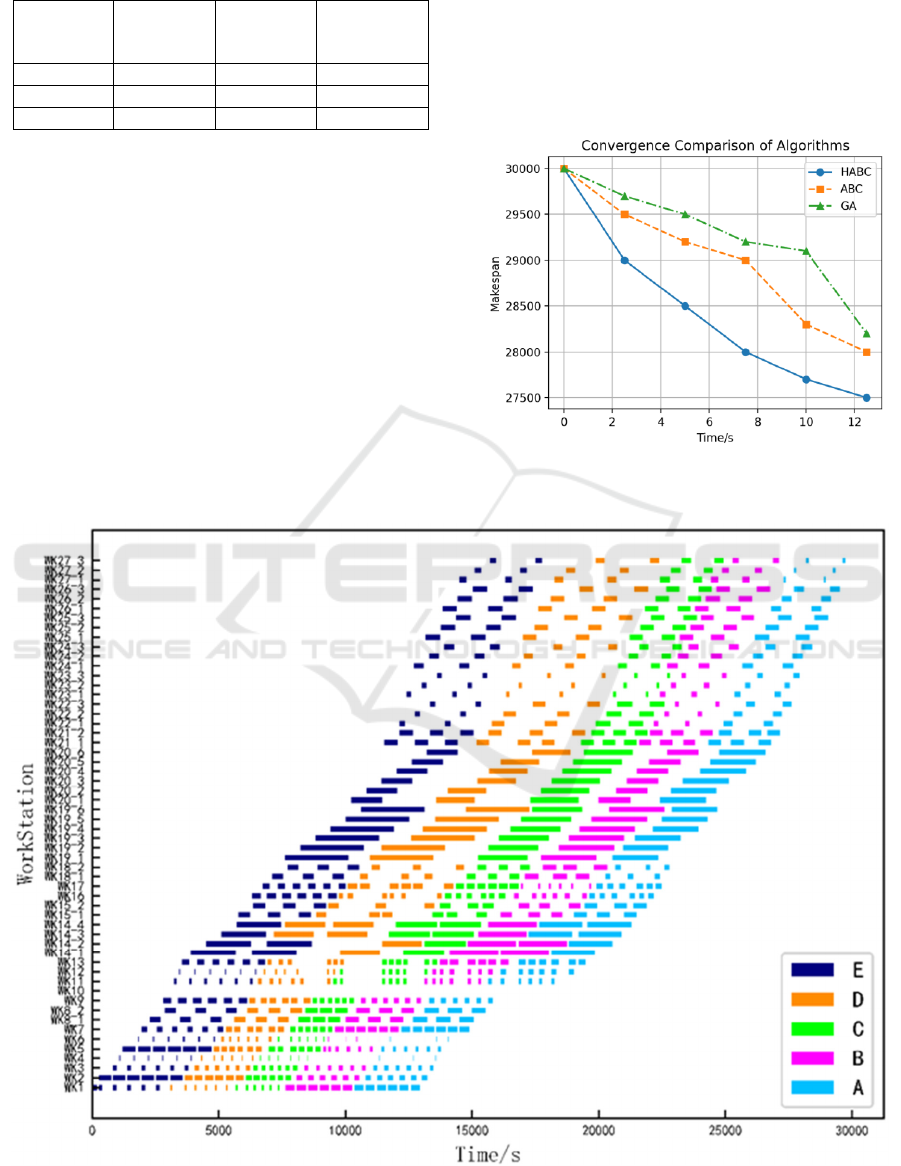
Table 6: Performance comparison of different algorithms

under real buffer scenarios.

Algorithm

Average

Makespan

(s)

Optimal

Makespan

(s)

Average

Blocking

Occurrences

ABC 27310 27120 139.2

GA 27532 27342 155.5

HABC 27103 26907 124.3

As shown in Table 6, HABC achieves a 1.62%

reduction in average makespan compared to GA and

reduces blocking occurrences by 25.1%,

demonstrating that its WPFE initialization and VNS

local search effectively alleviate blocking issues

caused by buffer constraints.

3.2 Algorithm Convergence Speed

Comparison

To visually demonstrate HABC’s efficiency

advantages during optimization, Figure 1 compares

the convergence curves of HABC, ABC, and GA. The

x-axis represents time ("Time/s"), and the y-axis

represents makespan ("Makespan"). In the initial

phase, all three algorithms start with a makespan of

30000. HABC rapidly converges from 30000 to

27500, ABC converges from 30000 to 28000, and GA

converges from 30000 to 28200. HABC demonstrates

rapid decline during the initial iteration phase (0–2s),

attributed to the high-quality initial solutions

provided by WPFE initialization.

Figure 1: Algorithm Convergence Curve Comparison

(Picture credit: Original)

Figure 2: Gantt Chart Under Original Buffer Configuration (Picture credit: Original)

HABC Algorithm Optimization for Hybrid Flow Shop Scheduling Under Blocking and Finite Buffer Constraints

165

As shown in the figure 1 and 2, HABC starts with an

initial makespan of approximately 30,000 and rapidly

reduces it using this initialization strategy. During the

mid-phase, the algorithm refines workpiece

sequences through VNS neighborhood search,

converging to 27,500 within a short time and

stabilizing. ABC shows slow decline in the first 2s,

later becoming trapped in local optima with

fluctuations of about ± 150. GA initially drops

quickly to 29,500 due to crossover-mutation

operations but stagnates in the mid-phase, ultimately

optimizing to 29,000 with fluctuations up to ±200.

By calculating the time required to reach 95% of the

optimal value, HABC requires only approximately 4

seconds, reducing time by about 42% and 51%

compared to ABC and GA, respectively.

3.3 Buffer Capacity and Efficiency

Figure 2 illustrates the Gantt chart of workpiece

scheduling under the original buffer configuration,

where the job launching sequence is determined by

the product name. The horizontal axis represents time

(in seconds), the vertical axis denotes processing

stages (1–27), and colored rectangles indicate

workpiece operations at corresponding stages. This

baseline scenario visually presents the process

timeline, serving as a reference for comparing

subsequent buffer adjustment experiments (Figures 3,

4).

To quantify the impact of buffer capacity on

scheduling, two comparative experiments were

designed:

Experiment 1: Buffer capacity between processes

14-15 was increased from 0 to 1.

Experiment 2: Buffer capacity C



between

processes 25-26 was reduced from 5 to 0.

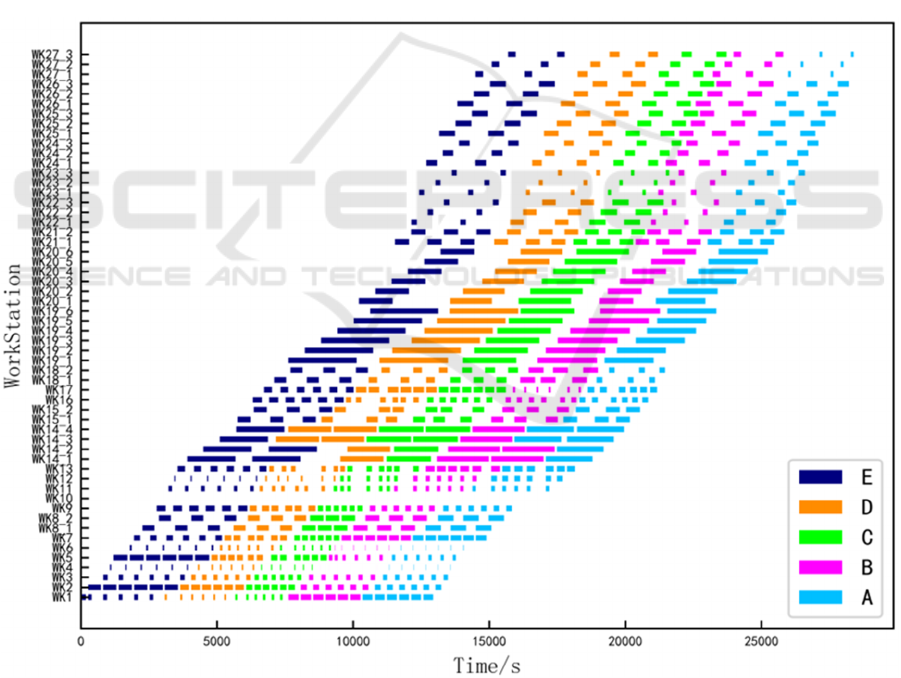
Figure 3: Comparison of Effects After Buffer Capacity Increase (Picture credit: Original)

Figure 3 shows the variation in Makespan under

different buffer capacities for processes 14-15. When

the capacity was 0, workpieces were directly blocked

after completing process 3 if the machine for process

4 was busy. With a capacity of 1, the buffer could

temporarily store 1 workpiece, reducing the

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

166

Makespan from 29,764 seconds to 28,426 seconds (a

4.5% reduction).

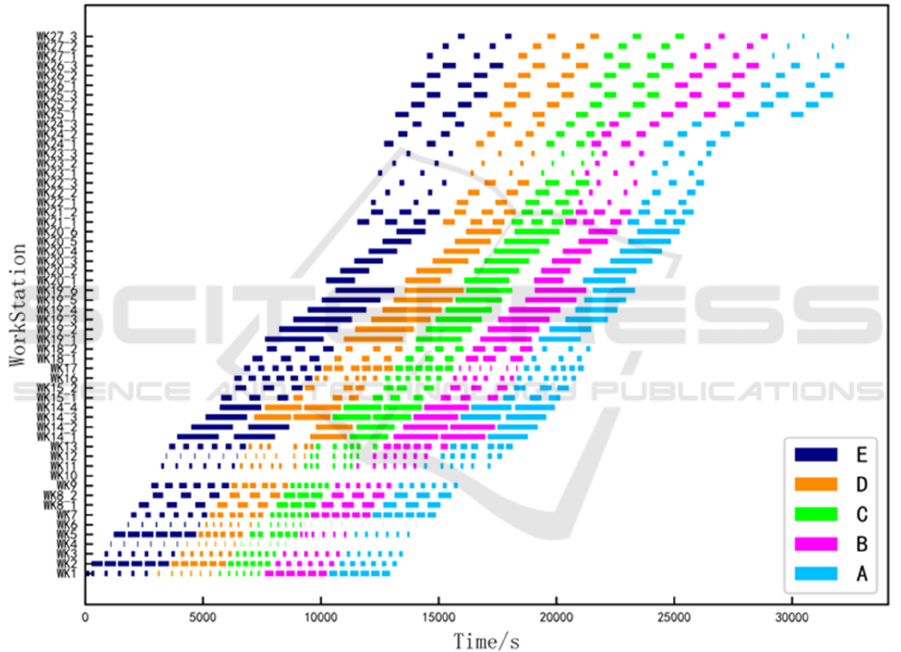
Figure 4 compares the impact of reducing buffer



capacity from 5 to 0 between processes 25-26 on

scheduling. When C



′s capacity is reduced to 0, the

buffer loses its temporary storage capability, causing

blocking occurrences to surge to 272 times/schedule

and prolonging the Makespan to 33,050 seconds.

Based on real "parallel machine/buffer" data from

Sany Heavy Industry, this study validates the

effectiveness of the HABC algorithm in

heterogeneous buffer scenarios through two

comparative experiments.

Buffer capacity is a critical constraint: Zero buffer

capacity causes concentrated blocking, significantly

increasing the makespan compared to buffered

scenarios, while unit buffer capacity can notably

alleviate blocking;

Algorithm superiority: HABC outperforms

traditional algorithms in both solution quality (1.61%

Makespan reduction) and convergence speed through

WPFE initialization and VNS local search, providing

a feasible solution for real-time scheduling in discrete

manufacturing enterprises.

Figure 4: Comparison of Effects After Buffer Capacity Reduction (Picture credit: Original)

4 CONCLUSIONS

This study focuses on the hybrid flow shop

scheduling problem based on the heterogeneous

buffers in SANY Heavy Machinery factories.

Through multiple experiments, the improved Hybrid

Artificial Bee Colony (HABC) algorithm is compared

with traditional algorithms (ABC, GA).

The HABC algorithm demonstrates significant

advantages in terms of solution quality, convergence

speed, and robustness. Compared with the GA, it

effectively reduces the makespan by 1.65%, and the

average number of blockages is also significantly

reduced. The HABC algorithm has the fastest

convergence speed, taking only about 4 seconds to

converge to 95% of the optimal value, which is

approximately 42% and 51% less time compared to

HABC Algorithm Optimization for Hybrid Flow Shop Scheduling Under Blocking and Finite Buffer Constraints

167

the ABC and GA algorithms respectively. The buffer

capacity, especially in the zero - buffer scenario, has

a significant impact on scheduling efficiency,

potentially leading to concentrated blockages and an

increase in makespan.

However, this study has certain limitations. The

current model does not fully consider complex

dynamic factors such as real - time order changes and

machine failures. In future research, more dynamic

adjustment mechanisms, such as dynamic buffer

capacity allocation based on real - time load, can be

introduced to further enhance the adaptability of the

algorithm in complex industrial scenarios. At the

same time, expanding the research to more industrial

application scenarios to verify the universality of the

algorithm is also an important direction for future

work. Overall, this study provides a feasible solution

for real - time scheduling in discrete manufacturing

enterprises, and the HABC algorithm shows great

potential in the optimal scheduling of actual

production.

REFERENCES

Fan, P., (2012). A Particle Swarm Optimization Algorithm

for Solving Flexible Flow Shop Scheduling Problems.

Journal of Changchun University of Technology

(Natural Science Edition), 33(5), 511-515.

Hu, Y., Yan, M., Ma, Y., (2006). A General Job-

Scheduling Method for Manufacturing Systems Based

on Intelligent Algorithms. Journal of Shanghai Jiao

Tong University, 40(10), 1701-1705.

Li, R., et al., (2024). A Review of Research on Hybrid Flow

Shop Scheduling Problems. China Mechanical

Engineering, 35(24), 2961-2972.

Luo, L., Wu, C., Chen, K., (2021). A Discrete Cuckoo

Search Algorithm for Solving Hybrid Flow Shop

Scheduling Problems. Journal of Chongqing Jiaotong

University (Natural Science Edition), 40(3), 369-375.

Mou, Y., Yan, C., Liu, Y., Sun, L., (2020). A Scheduling

Method for Flexible Flow Shops Considering Energy

Consumption and Completion Time. China Science and

Technology Paper Online, 15(2), 1-8.

Qi, L., Zhao, Q., (2012). A Hybrid Particle Swarm

Optimization Algorithm for Solving Flow Shop

Scheduling Problems. Computer Engineering and

Applications, 48(9), 24-28.

Song, K., et al. (2021). Batch Scheduling Optimization

Based on a Three-level Hierarchical Ant Colony

Algorithm. Control and Decision, 36(8), 1953-1960.

Xie, T., et al., (2015). An Improved Migratory Bird

Optimization Method for Hybrid Flow Shop

Scheduling Problems. Computer Integrated

Manufacturing Systems, 21(8), 2099-2107.

Yuan, D., (2021). Multi-objective Scheduling for Hybrid

Flow Shops with Limited Buffers. Acta Scientiae

Technicae, 43(11), 1573-1582.

Zhang, P., Pan, L., Li, D., (2021). A Hybrid Artificial Bee

Colony Algorithm for Flow Shop Scheduling with

Limited Buffers. Computer Integrated Manufacturing

Systems, 27(4), 1034-1043.

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

168