Construction of College Students' Happiness Index Evaluation Model

and Optimization of Budget Allocation—Integrated Application of

Analytic Hierarchy Process and Linear Programming

Peiwen Luo

College of Mathematic and Statistic, Chongqing University, Chongqing, 400000, China

Keywords: College Students, Happiness Index, AHP, Linear Programming, Budget Optimization.

Abstract: The College students constitute a distinct demographic characterized by strong consumption desires coupled

with limited financial resources, which poses challenges to their overall well-being as measured by the

happiness index. This study aims to enhance the happiness index of college students by first collecting

empirical data on the allocation proportions of living expenses and their respective contributions to happiness

through structured questionnaire surveys. The Analytic Hierarchy Process (AHP) employing a 1–9 scale was

utilized to quantitatively assess the happiness index associated with each expenditure category, with

subsequent consistency testing of the judgment matrix confirming the validity of the evaluations. A

constrained linear programming model was then developed, defining the maximization of the aggregate

happiness index as the objective function and treating the proportional distribution of living expenses as

decision variables. By optimizing these allocations, the model seeks to maximize overall student happiness.

Validation through a case study on a randomly selected participant’s expenditure data demonstrated a

substantial increase in the happiness index post-optimization, thereby confirming the model’s applicability

and efficacy. This integrative methodological approach combining AHP and linear programming provides a

novel framework for the quantitative assessment and optimization of subjective well-being among college

students, offering significant implications for targeted financial planning and welfare improvement strategies.

1 INTRODUCTION

From the perspective of consumption, college

students, as an important component of the social

population, have consumption levels that largely

reflect the overall development of the national

economy. Whether their consumption structure is

scientific and reasonable not only affects their own

quality of life but also relates to their personal

financial stability (Gu, 2024). On one hand, college

students tend to have strong consumption desires

while lacking comprehensive spending plans, which

often leads to situations where their consumption

concepts are advanced, but their actual consumption

capacity is insufficient. On the other hand, their

sources of income are relatively singular, with the

vast majority relying on financial support from their

parents for living expenses (Chen, 2020). Based on

these two conditions, it can be observed that the

https://orcid.org/0009-0008-6719-9751

income and expenditure patterns of college students

are relatively simple, making them easier to

investigate and optimized yet such efforts are also

highly necessary. From the perspective of happiness

index, the college stage plays a critical role in the

transmission of knowledge and the cultivation of

skills for future labour forces. Therefore, ensuring the

well-being of college students is not only a key factor

in promoting effective learning, but also a proper and

necessary approach in line with the goals of 21st-

century education outcomes (Cosmas et al., 2022).

Consumer behaviour refers to the comprehensive

manifestation of consumers' psychological needs,

purchasing motivations, consumption intentions, and

their actual behaviours (Khairuddin and Mahmud,

2020). The happiness index, on the other hand, is a

quantifiable indicator artificially designed to evaluate

the degree of happiness. By combining the two

aspects-consumer behaviour and the happiness index-

it becomes evident that the sense of satisfaction

Luo, P.

Construction of College Students’ Happiness Index Evaluation Model and Optimization of Budget Allocation—Integrated Application of Analytic Hierarchy Process and Linear Programming.

DOI: 10.5220/0014323900004718

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2025), pages 151-156

ISBN: 978-989-758-792-4

151

derived from consumption can influence consumers'

perceived happiness (Shi et al., 2024). Therefore, it

can be reasonably understood that appropriate

consumer behaviour contributes positively to the

improvement of the happiness index. Conversely,

inappropriate or irrational consumption behaviour

can have adverse effects on the happiness index of

college students (Ong et al., 2022).

Existing research generally focuses on the

economic attributes of consumer behaviour,

emphasizing objective indicators such as the Engel

coefficient, while often overlooking the underlying

mechanisms linking consumption choices to

subjective well-being. Although methods such as

Analytic Hierarchy Process (AHP) and linear

programming have been applied in the evaluation of

quantitative data and the study of economic issues,

limited attention has been given to the combined

analysis of college students’ living budgets and the

optimization of quantified happiness indices (Saaty,

2008; Chen and Wang, 2019).

This study innovatively constructs a three-tier

analytical framework of “Consumption Clustering –

Happiness Quantification – Budget Optimization.”

First, by integrating data from questionnaire surveys

and publicly available databases, key expenditure

dimensions in daily life are identified. Subsequently,

an improved Analytic Hierarchy Process (AHP)

model-enhanced with λ-consistency checks and

modified using the entropy weight method-is

employed to quantify the contribution weights of each

dimension to the happiness index (Wen et al., 2018).

Finally, a constrained linear programming model is

established, using the minimum necessary

expenditure as the boundary condition, to solve for

the optimal budget allocation scheme under the

objective function of maximizing the happiness

index. Compared with traditional single-dimensional

economic models, this framework achieves a

dynamic coupling between the objective

quantification of consumption behaviour and the

subjective perception of well-being, thereby

identifying an optimal balance point for budget

optimization and happiness improvement among

college students.

2 METHODS

2.1 Data Resource

The quantitative data on college students’

consumption-related happiness, as well as data on the

primary expenditure categories and their proportions

in students’ living expenses, were obtained through a

questionnaire survey. The survey was conducted

among 100 undergraduate students from various

regions.

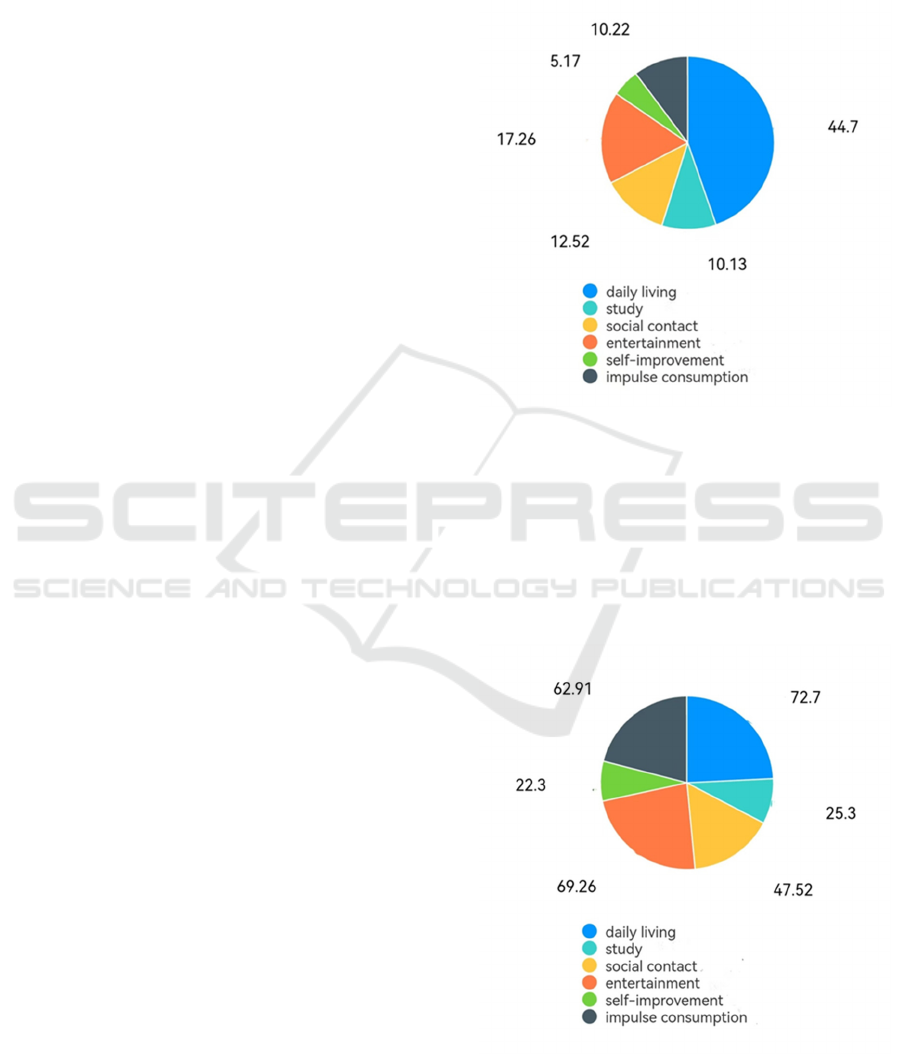
Figure 1: Chart of College Students’ Living Expense

Categories and Their Proportions (Picture credit: Original).

The figure 1 above presents the statistical distribution

of the average proportions of college students’ living

expenses by category, based on data collected

through the questionnaire survey. It reflects the major

expenditure categories and their approximate shares

in the overall budget.

Figure 2: Chart of Contribution Proportions to the

Improvement of College Students’ Happiness (Picture

credit: Original).

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

152

The figure 2 above presents the average values of the

perceived contribution of each expenditure category

to happiness improvement, based on data collected

through the questionnaire survey (original

proportions normalized from 300%). It reflects a

simplified quantitative assessment of how each

spending category contributes to the enhancement of

college students’ happiness.

2.2 Variable Description

The table 1 explains the variables that need to be used

in the subsequent mathematical modeling process and

their explanations.

Table 1: Table of variable description

Variable Descri

tion

𝑐



Quantitative data of the relatively

subjective comprehensive evaluation of

the happiness index ratings for each

expenditure category of college students’

living expenses, based on the

questionnaire results.

𝑥



Proportion of each expenditure category

in the total living expenses of college

students (calculated as percentages; the

percentage sign is omitted in subsequent

tables).

M The total happiness index calculated by

summing the happiness indices of all

expenditure categories for college

students’ living expenses.

2.3 Method Overview

This paper utilizes data obtained from a survey to

establish a rating system for each category of living

expenses. A judgment matrix is constructed, and the

consistency of the matrix, along with the value of its

determinant, is used to validate the rationality of the

rating system. The happiness rating index for each

expenditure category is then derived. Subsequently,

an objective function is formulated, and constraints

are set based on the relevant data of college students'

living expenses. Using linear programming, the

proportion of each expenditure category is optimized,

aiming to maximize the overall happiness index.

3 RESULTS AND DISCUSSION

3.1 Data Analysis and Production

3.1.1 Quantitative Data for Happiness Index

Ratings

Based on the collected happiness rating data, the 1-9

scale method from the Analytic Hierarchy Process

(AHP) is used to quantify the happiness index-that is,

each expenditure type is rated on a scale from 1 to 9

according to its relative importance (the higher the

score, the more important the category). The

consumption types are categorized into six groups:

daily living, study, social contact, entertainment, self-

improvement, and impulse consumption. The

happiness rating indices are rounded to the nearest

integer to maintain consistency, and the resulting data

are presented in the following table 2:

Table 2: Happiness Index Rating Table

Daily living Study Social contact

72 5

Entertainment

Self-

rovement

Impulse

consum

tion

72 6

The table 2 above presents a scientific quantification

of the happiness index using the 1-9 scale method,

based on the proportional distribution of the

simplified happiness index ratings. A pairwise

comparison matrix is constructed based on the

relative importance between the six influencing

factors, as shown below (Table 3):

Table 3: Judgment Matrix

1 3/7 5/7 1 2/7 6/7

7/3 1 5/3 7/3 2/3 2

7/5 3/5 1 7/5 2/5 6/5

1 3/7 5/7 1 2/7 6/7

7/2 3/2 5/2 7/2 1 3

7/6 1/2 5/6 7/6 1/3 1

Construction of College Students’ Happiness Index Evaluation Model and Optimization of Budget Allocation—Integrated Application of

Analytic Hierarchy Process and Linear Programming

153

The consistency index (CI) is defined as:

𝐶𝐼 =

𝜆−𝑛

𝑛−1

(1)

Where, n represents the order of the judgment matrix,

and λ denotes the maximum eigenvalue of the matrix.

Next, the random index (RI), which corresponds to

the value of n, is obtained from a standard reference

table 4:

Table 4: Random Index (RI) Table (Bi, 2023)

n 3 4 5 6 7 8

RI 0.58 0.90 1.12 1.24 1.32 1.41

The table 4 above presents an empirically derived

statistical value associated with the matrix dimension

n, which is used to assess whether the current

judgment matrix demonstrates greater consistency

than a randomly generated matrix.

Finally, the consistency ratio (CR) is calculated as:

𝐶𝐼 =

𝐶𝐼

𝑅𝐼

(2)

The computation yields CR ≈ 1.43 × 10⁻¹⁶ < 0.1,

which is infinitesimally close to zero. Therefore, the

consistency requirement is satisfied, and the

rationality of the quantified happiness index ratings is

validated, allowing for further data processing.

3.1.2 Range of College Students’ Living

Expense Categories

Based on the collected data on college students’

living expense categories and their corresponding

proportions, the mean (μ) and standard deviation (σ)

for each expenditure category are calculated. To

eliminate the influence of outliers on the normal

range, the interval μ ± σ, which covers approximately

65.26% of the data, is adopted as the reasonable range

for the proportion of each living expense category.

By calculating, the mean proportion μ and standard

deviation σ for each expenditure category were

obtained. To simplify the computational complexity

during model construction, the values were rounded.

The results are as follows:

Table 5: Table of Mean Proportions (μ) for Each

Expenditure Category

Dail

livin

Stud

Social contact

45 10 13

Entertainment

Self-

rovement

Impulse

consum

tion

17 5 10

Table 6: Table of Standard Deviations (σ) of Proportions

for Each Expenditure Category

Daily living Study Social contact

17 6 11

Entertainment

Self-

rovement

Impulse

consum

tion

13 8 9

These two variables from table 5 and 6 can be used to

calculate the normal range of living expense

proportions for each expenditure category among

college students. If the lower bound, calculated as μ -

2σ, is less than 0, it is reasonably adjusted to 0. The

final ranges are shown as follows:

Table 7: Table of Normal Ranges for College Students’

Living Expense Proportions by Expenditure Category

Dail

livin

Stud

Social contact

（28,62） (4,16) （2,24）

Entertainment

Self-

rovement

Impulse

consum

tion

(

4,30

)

(

0,13

)

(

1,19

)

The above table 7 can basically clarify the normal

range of each expenditure direction, that is, the upper

and lower limits of constraints.

3.2 Model Building

3.2.1 Define Decision Variables

Based on the analysis of existing data, it was found

that the data type suitable for adjustment and

optimization is the proportion of college students’

living expenses allocated to different categories.

Therefore, this paper defines 𝑥



is the proportion of

living expenses allocated to the 𝑖 category. This

approach to defining decision variables focuses the

study on the proportions of living expenses, thereby

avoiding difficulties in investigating and collecting

data caused by the diverse and complex family

backgrounds of college students.

3.2.2 Establish the Objective Function

To establish the objective function, the goal must be

clarified: using a mathematical model to optimize the

proportions of college students’ expenditures to

maximize the overall happiness index. Based on the

existing data and analytical results, linear

programming is identified as the optimal method for

this optimization. Therefore, the objective function

can be defined as follows: 𝑀=𝑐



𝑥



. Where, 𝑐



represents the happiness index associated with each

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

154

expenditure category, and 𝑥



denotes the proportion

of living expenses allocated to each category.

By optimizing this objective function through

adjusting the decision variables, the maximum overall

happiness index can be achieved.

3.2.3 Set General Constraints

Based on previous calculations, the normal range of

the decision variables, the proportions of college

students’ living expenses allocated to each category-

can be clearly defined as: (𝜇



−σ



，𝜇



+σ



), where

μᵢ represents the meaning of the data for the ith

expenditure category, and σᵢ represents the standard

deviation of the data for the ith category. By using the

normal range of college students’ living expense

proportions as constraints on the decision variables,

approximately 98% of the typical data is included,

while the influence of outliers is effectively excluded.

3.2.4 Set Type Constraints

Individual consumption behaviors and habits vary

and tend to be persistent over time. In other words,

long-established consumption habits are difficult to

change drastically in a short period, and abrupt

adjustments to expenditure structures are neither

practical nor scientific. This consideration represents

an innovative aspect of this study. Considering the

diversity of consumption habits among college

students, this paper classifies the population into two

types: impulsive consumers and non-impulsive

consumers.

When the proportion of impulse consumption

exceeds 10% (approximately μ), the individual is

classified as an impulsive consumer. This personality

type is characterized by a lack of clear consumption

plans and a relatively high share of impulsive

expenditures in living expenses. The emotional value

provided by this behavior, i.e., the enhancement

effect on the happiness index, is more pronounced.

Accordingly, this paper sets the constraint on impulse

consumption proportion as: (0.1, μ + σ).

Conversely, when the impulse consumption

proportion does not exceed 10% (approximately μ),

the individual is classified as a non-impulsive

consumer. This personality type features well-defined

consumption plans and a relatively low share of

impulsive expenses, with a weaker contribution to the

improvement of the happiness index. Thus, the

constraint on impulse consumption proportion for this

type is set as: (μ − σ, 0.1).

By incorporating these type-specific constraints,

the model scientifically addresses the optimization

needs of different consumption habit groups among

college students, further enhancing their overall

happiness index.

3.3 Model Application

A randomly selected student's living expense

allocation from the questionnaire is used for

optimization. The original proportion data for each

expenditure category is as follows (Table 8, 9):

Table 8: Table of Original Living Expense Proportions.

Dail

livin

Stud

Social contact

40 10 15

Entertainment

Self-

rovement

Impulse

consum

tion

15 10 10

Based on the formula, the original total happiness

index is calculated to be 5.6. The established

mathematical model is then applied to optimize the

living expense proportions. The optimized results are

as follows:

Table 9: Table of Optimized Living Expense Proportions.

Daily living Study Social contact

62 4 2

Entertainment

Self-

improvement

Impulse

consumption

30 0 2

By applying the objective function again, the

optimized total happiness index is calculated to be

6.74, which is significantly higher than the original

value of 5.6. This result validates the effectiveness

and rationality of the proposed model.

4 CONCLUSION

Through the above discussion, this paper constructs a

mathematical model that first quantifies the happiness

index ratings associated with each category of college

students’ living expenses. The model then optimizes

the allocation of these expenses to maximize the total

happiness index. To validate the model’s

effectiveness, a randomly selected student's data was

used for optimization, and the increase in the total

happiness index from pre-optimization to post-

optimization confirmed the model’s feasibility.

This model addresses the challenge of

coordinating college students’ living expense

Construction of College Students’ Happiness Index Evaluation Model and Optimization of Budget Allocation—Integrated Application of

Analytic Hierarchy Process and Linear Programming

155

allocations and contributes to enhancing their overall

happiness index.

However, the model has certain limitations. For

instance, it only considers constraints based on the

average values of each indicator, without accounting

for the differentiated preferences of students with

varying personalities. This presents a potential

direction for future refinement.

REFERENCES

Bi, L., (2023). Research on the Construction of a Complete

Evaluation Index System for Higher Mathematics

Based on the Analytic Hierarchy Process. Shandong

Vocational College of Engineering and Technology.

Chen, L., Wang, Y., (2019). Optimal Personal Financial

Planning Using Linear Programming under Uncertainty.

Journal of the Operational Research Society, 70(9),

1481-1493.

Chen, P., (2020). Investigation and Analysis of College

Students’ Consumption Structure. School of

Mathematics and Computer Science, Hengshui

University.

Cosmas, G., et al., (2022). The effects of resiliency on

university students' happiness and life effectiveness

amid the covid-19 pandemic: religious faith stands as a

moderator. International Journal of Religion &

Spirituality in Society, 12(2).

Gu, K., (2024). Research on the Impact of E-commerce on

Urban-Rural Integration Development. Shandong

University of Finance and Economics.

Khairuddin, M. T., Mahmud, Z., (2020). Modelling the

effects of psychological well-being attributes on

students' happiness. Journal of Physics: Conference

Series, 1496(1).

Ong, A. K., et al., (2022). Factors affecting students'

happiness on online learning during the covid-19

pandemic: a self determination theory approach.

International Journal of Information and Education

Technology.

Saaty, T. L. (2008). Decision Making with the Analytic

Hierarchy Process. International Journal of Services

Sciences, 1(1), 83-98.

Shi, Y., Wu, S., Yuan, Y., (2024). Research on the

Influence Mechanism of Different Types of Sustainable

Consumption Behavior on Consumer Happiness. Asian

Journal of Economics, Business and Accounting, 24(9),

135-145.

Wen, N. L., Guo, Y. H., Ji, J. S., (2018). A study on the

present situation and educational countermeasures of

contemporary female college students' happiness.

Education Teaching Forum.

EMITI 2025 - International Conference on Engineering Management, Information Technology and Intelligence

156