A Hybrid SARIMAX-SVR Model for Drug Demand Prediction

Rithagia Palelleng

and Novy N. R. A. Mokobombang

Department of Informatics, Faculty of Engineering, Universitas Hasanuddin, Gowa, South Sulawesi, Indonesia

Keywords: Forecasting, SARIMAX, SVR, Hybrid Model, Machine Learning.

Abstract: Accurate prediction of drug demand is a critical challenge in Indonesia’s National Health Insurance (JKN)

system, where misestimation can lead to two major problems: overstock, resulting in financial inefficiency,

and stockouts, which directly disrupt patient therapy. Traditional time-series models such as ARIMA and

SARIMA are often insufficient to capture nonlinear fluctuations and complex seasonal patterns in drug

demand. To address this issue, this study proposes a hybrid prediction model that integrates the Seasonal

Autoregressive Integrated Moving Average with Exogenous Variables (SARIMAX) and Support Vector

Regression (SVR). The SARIMAX component captures linear trends and seasonality by incorporating

external factors such as patient volume and e-catalog procurement status, while the SVR component corrects

nonlinear residual patterns. The dataset consisted of daily drug consumption records, patient visits, and

procurement data from the Dr. Tadjuddin Chalid Makassar Hospital. The Experimental results demonstrate

that the hybrid SARIMAX–SVR model reduces the Root Mean Square Error (RMSE) by approximately 44%

compared to standalone SARIMAX, across different drug demand categories. This approach provides a more

adaptive, accurate, and computationally efficient forecasting framework to support decision-making in

pharmaceutical supply chain management under the JKN scheme.

1 INTRODUCTION

The availability of the right amount and time of

medicine is a vital element in maintaining the quality

of health services, especially in the National Health

Insurance (JKN) system, which covers the majority

of the Indonesian population. Inaccuracies in

planning drug needs can lead to two main problems:

overstock, which causes cost inefficiencies, or

stockouts, which have a direct impact on the

continuity of patient therapy. In practice, this

challenge is increasingly complex because the

dynamics of drug demand are influenced by various

factors such as seasonal disease trends, fluctuations

in the number of patient visits, and limitations in e-

catalog-based procurement systems.

In article (Satibi et al., 2020), the drug supply

chain management system in the JKN era still faced

problems in ensuring the availability of drugs on an

ongoing basis. This is exacerbated by the lack of

utilization of data-based predictive approaches in the

demand planning process. Traditional time series

methods such as ARIMA or SARIMA are often used

https://orcid.org/0009-0003-5389-4634

https://orcid.org/0000-0001-5706-939X

for demand forecasting but tend to be limited in

handling non-linear patterns and instability that are

common in drug demand data.

To accommodate such complexity, the Seasonal

Autoregressive Integrated Moving Average with

Exogenous Variables (SARIMAX) model offers

advantages in modeling both trend and seasonality

while allowing the inclusion of exogenous variables

such as patient numbers and e-catalog status (Alharbi

& Csala, 2022). However, despite these strengths,

SARIMAX remains limited in capturing nonlinear

variability and sudden spikes in demand.

Recent studies have increasingly adopted hybrid

time-series models that integrate statistical and

machine learning techniques for healthcare

forecasting. For instance, Zhao and Zhang (2023)

proposed a SARIMA–ETS–SVR hybrid for

influenza incidence prediction, achieving up to 18%

accuracy improvement. Similarly, Benitez et al.

(2023) combined SARIMAX and LSTM for solar

energy prediction, showing that hybrid architectures

can effectively capture both linear and nonlinear

temporal structures. In the pharmaceutical domain,

(Alzami et al., 2024) employed SARIMAX with

Palelleng, R. and Mokobombang, N. N. R. A.

A Hybrid SARIMAX-SVR Model for Drug Demand Prediction.

DOI: 10.5220/0014272400004928

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Innovations in Information and Engineering Technology (RITECH 2025), pages 209-216

ISBN: 978-989-758-784-9

209

exogenous weather factors to forecast food and

beverage demand, while (Alsaber et al., 2024)

demonstrated the potential of SVR in predicting

biologic therapy response among rheumatoid arthritis

patients.

Building on these findings, the present study

extends hybrid SARIMAX–SVR modeling into the

context of hospital drug demand forecasting—an area

rarely explored in Indonesia—by integrating patient

volume and e-catalog procurement data as exogenous

factors.

Based on these problems, this study proposed a

hybrid SARIMAX-SVR model approach to improve

the accuracy of predicting drug needs in the JKN

system. The data used were daily drug supply data

from the Central General Hospital (RSUP) Dr.

Tadjuddin Chalid Makassar for the last two years,

complemented by data on the number of patient visits

and e-catalog procurement status as exogenous

variables. The main objectives of this study were to

(1) develop a SARIMAX-SVR-based drug demand

prediction model, (2) evaluate the performance of the

model compared to conventional approaches, and (3)

provide a decision support system that can be

implemented in data-based pharmaceutical logistics

planning at the national health service scale.

2 RESEARCH METHOD

This study proposed a drug demand prediction

approach based on a hybrid SARIMAX-SVR model.

The methodology consisted of three main stages:

SARIMAX model building, SVR model training

based on SARIMAX residuals, and prediction

performance evaluation using the Root Mean

Squared Error (RMSE) metric. The SARIMAX

model was chosen to capture the seasonal and linear

components of drug demand by incorporating

external factors, such as patient volume and

procurement policy. However, because SARIMAX

may fail to explain nonlinear dynamics and sudden

spikes in demand, Support Vector Regression (SVR)

with a Radial Basis Function (RBF) kernel was

applied to model the residual errors. The RBF kernel

was selected for its proven ability to capture

complex, non-linear relationships without excessive

overfitting, while maintaining computational

efficiency, making the SARIMAX–SVR hybrid

model both accurate and practical for hospital-level

forecasting systems. The dataset used includes daily

inventory data of more than 100 types of drugs at Dr.

Tadjuddin Chalid Hospital Makassar for three years

(2023-2024), as well as data on the number of patient

visits and e-catalog procurement status as exogenous

variables.

2.1 SARIMAX Model

Box and Jenkins (Pankratz.A, 2019) proposed the

ARIMA model, a series forecasting method. The

basic idea of the ARIMA model is to consider the

observational dataset over time as a random set and

use a mathematical model to approximate this

sequence.

Recent studies have proposed various hybrid

forecasting approaches that integrate SARIMAX

with deep learning or ensemble-based machine

learning methods such as LSTM and XGBoost to

address the limitations of linear time-series models.

A study by (Benitez et al., 2023) applied a hybrid

SARIMAX–LSTM model to solar irradiance

forecasting in the Philippines. The study found that

although the hybrid model outperformed standalone

SARIMAX or LSTM in certain regions, it did not

consistently produce superior results across all

datasets. The performance was highly dependent on

the data characteristics, and the model required

substantial computational resources and tuning

efforts. In another study (Lee et al., n.d.),

SARIMAX–LSTM and SARIMAX–SVR were used

for electric load forecasting. Their findings showed

that SARIMAX–LSTM performed well in capturing

peak demands, whereas SARIMAX–SVR achieved

better overall accuracy and stability in multivariate

settings.

In recent epidemiological research(Man et al.,

2023), a SARIMA–XGBoost hybrid model was used

to predict daily incidence of hand, foot, and mouth

disease (HFMD) in Xinjiang, China. The study

followed a two-stage modeling process: first, fitting

a SARIMA model, followed by residual correction

using XGBoost with optimized hyperparameters,

such as max depth and learning rate, via

GridSearchCV. The hybrid model achieved a

significantly lower RMSE of 112.51, compared to

147.51 (SARIMA alone), 152.75 (XGBoost alone),

129.43 (LSTM), and 167.01 (SVR), demonstrating

its superiority and improved R² by up to 25% over

base models.

The SARIMAX model is a form of SARIMA that

includes independent (exogenous) variables. The

SARIMAX model is denoted as (𝑝, 𝑑, 𝑞)(𝑃, 𝐷,

𝑄)𝑆(𝑋), where 𝑋 represents the exogenous variables.

These independent variables in the SARIMAX model

can be modeled using a multiple linear regression

equation. The general form of the SARIMAX model

(𝑝,𝑑,𝑞)(𝑃,𝐷,𝑄)



(𝑋) represents the linear

relationship between drug demand and its past

RITECH 2025 - The International Conference on Research and Innovations in Information and Engineering Technology

210

observations, seasonal components, and external

factors. This relationship can be expressed as follows

[8]:

𝑌



= 𝑐 +

∑

𝜑



𝑌







∑

𝜃



𝜀







∑

𝛷



𝑌

·





∑

𝛩



𝜀

·





+ 𝛽



+ 𝛽



𝑉

,

𝛽



𝑉

,

+ ⋯ + 𝛽



,

+ 𝜀



(1)

Where:

𝑌𝑡 = drug demand at time t

C = constant

p,d,q = orders of the non-seasonal ARIMA

components (autoregressive,

differencing, moving average)

P,D,Q,s = orders of the seasonal ARIMA

components (seasonal AR, seasonal

differencing, seasonal MA, and

seasonal period)

Φi = autoregressive coefficients

Θj = moving average coefficients

Φk,Θl = seasonal autoregressive and moving

average coefficients

Vj,t = exogenous variable jjj at time ttt

(e.g., number of patients, e-catalog

status, weekday dummy)

𝛽0, 𝛽1,..,𝛽m = regression coefficients of the dummy

variables

= residual (white noise)

In this formulation, 𝑌



denotes the drug demand at

time 𝑡, while the terms 𝜙



, 𝜃



, Φ



, and Θ



represent

the autoregressive (AR) and moving average (MA)

coefficients for both non-seasonal and seasonal

components. Exogenous variables 𝑉

,

— such as

patient volume or e-catalog status — are included

with regression coefficients 𝛽



,𝛽



,…,𝛽



. The

residual term 𝜀



captures random disturbances or

unexplained variation. This formulation allows the

SARIMAX model to incorporate both temporal

dynamics and external influences in predicting

hospital drug demand

In this research, the SARIMAX model was fitted

using the Auto-ARIMA procedure, which

automatically selects the optimal (p,d,q)(P,D,Q)s

parameters based on information criteria (AIC/BIC),

while simultaneously including the exogenous

variables. This ensures that both the temporal

dynamics (trend, seasonality, autoregressive and

moving average components) and the external

influences are captured in the model.

It is important to note that the formulation above

is consistent with previous SARIMAX-based

forecasting studies. For instance (Alharbi & Csala,

2022)(Alzami et al., 2024)applied a SARIMAX

model with exogenous weather variables in food and

beverage demand forecasting, and [MDPI, 2022]

used a similar SARIMAX formulation to forecast

container throughput at the Port of Singapore. Both

studies explicitly adopted the same mathematical

structure, combining ARIMA components with

seasonal adjustments and exogenous regressors, thus

validating the methodological basis of the present

research

The Seasonal Autoregressive Integrated Moving

Average with Exogenous Variables (SARIMAX)

model was used to capture the linear components of

drug demand patterns, including trends and

seasonality. The model also integrates exogenous

variables, namely, the number of patients and

ecatalog status, which are assumed to have an

influence on drug demand. The SARIMAX model is

trained on the training data and produces an initial

predicted value along with the residual (the difference

between the prediction and actual realization).

2.2 SVR Model (Support Vector

Regression)

To address nonlinear patterns that cannot be fully

explained by SARIMAX, the residuals from the

SARIMAX model were remodeled using the Support

Vector Regression (SVR) method. SVR constructs a

regression function in a high-dimensional feature

space by mapping the input data through a kernel

function, enabling the model to capture complex

relationships To capture the nonlinear relationships

left unexplained by SARIMAX, the residuals are

modeled using the Support Vector Regression (SVR)

function. The general regression form of SVR is

defined as follows (Zhao & Zhang, 2023):

𝑓

(

𝑥

)

∑(

𝛼



− 𝛼



∗

)

𝐾

(

𝑥



,𝑥

)





+ 𝑏 (2)

where:

• m = number of support vectors

• α

and α

= Lagrange multipliers obtained from

the optimization problem,

• K (x

,x) = kernel function that measures the

similarity between support vectors x

dan x,

• b = bias term.

In this equation, 𝑚 represents the number of

support vectors, while 𝛼



and 𝛼



∗

are Lagrange

multipliers obtained through optimization. The kernel

function 𝐾

(

𝑥



,𝑥

)

measures the similarity between the

input vectors, and 𝑏 denotes the bias term. This

formulation allows SVR to construct a regression

A Hybrid SARIMAX-SVR Model for Drug Demand Prediction

211

surface that best fits the residual patterns from

SARIMAX, minimizing prediction error within a

defined margin.

The performance of SVR largely depends on the

choice of kernel function, which transforms the input

space into a higher-dimensional feature space to

capture nonlinear relationships. The general

definition of the kernel function is given by Equation

(3) (Zhao & Zhang, 2023)(Alsaber et al., 2024):

𝐾𝑥



,𝑥



=  𝜑

(

𝑥



)

,𝜑𝑥



 (3)

Where

are basis functions representing the feature

mapping ϕ(x).

Among the various kernel functions, this study

employed the Radial Basis Function (RBF) kernel,

expressed as:

𝐾𝑥



,𝑥



=exp



−𝛾 𝑥



− 𝑥









(4)

In this equation, 𝐾𝑥



,𝑥



represents the kernel

value, which measures the similarity between two

input vectors. The parameter 𝛾controls the influence

of individual data points — a larger 𝛾produces a more

localized kernel, making the model more sensitive to

sudden changes or spikes in drug demand. The term

∥𝑥



−𝑥



∥



denotes the squared Euclidean distance

between the two vectors. This function therefore

expresses an exponential similarity: when two inputs

are very close, the kernel value approaches 1; as the

distance increases, the kernel value rapidly decays

toward 0.

The SVR model used default hyperparameters (C

= 1.0, ε = 0.1, γ = ' scale') to maintain computational

efficiency and focus on evaluating the hybrid model.

Notably, benchmarks across multiple datasets have

found default hyperparameter settings to perform

non-inferiorly compared to tuned values, supporting

the validity of this pragmatic approach. The RBF

kernel was chosen because of its flexibility and

robustness in modeling nonlinear, fluctuating drug

demand data

2.3 Evaluation Model

A performance evaluation was performed using the

Root Mean Squared Error (RMSE) metric to measure

the average deviation between the predicted and

actual values. The RMSE is used because it is

sensitive to outliers and can reflect the overall

prediction error. To evaluate prediction accuracy, this

study employs the Root Mean Squared Error (RMSE)

metric, which measures the average magnitude of

prediction errors. It is defined as follows (Zhao &

Zhang, 2022):

𝑅𝑀𝑆𝐸 = √((1/𝑛) ∑_(𝑡 = 1)^𝑛(𝑦



− ŷ



)^2 ) (5)

Where:

𝑦



= actual demand at time 𝑡,

𝑦



= predicted demand at time 𝑡,

𝑛= number of observations.

In this formula, 𝑛 denotes the number of

observations, 𝑦



is the actual value, and 𝑦



is the

predicted value. Lower RMSE values indicate better

model performance. Because RMSE penalizes large

deviations more strongly, it is particularly suitable for

assessing drug demand forecasts where occasional

spikes can greatly influence hospital inventory

decisions.

RMSE was selected because of its sensitivity to

large deviations, making it appropriate for evaluating

the forecasting accuracy of hospital demand data. The

models were evaluated under two scenarios: a single

SARIMAX model and a hybrid SARIMAX-SVR

model (combined SARIMAX prediction and SVR

correction based on residual data). Comparisons were

made for all drug types and averaged by drug therapy

category to determine the consistency of the model

performance.

In terms of computational cost, the SARIMAX

model required around 2.1 seconds per drug using

stats models, while the SVR correction stage added

4.6 seconds per drug with GridSearchCV. Overall,

the hybrid SARIMAX–SVR model completed

training and prediction in less than seven seconds per

drug, making it feasible for batch forecasting in

hospital systems. Compared to models like

SARIMAX–LSTM, which may take over 20 seconds

per drug, SARIMAX–SVR offers a more efficient

and scalable solution.

3 RESULT AND DISCUSSION

Experiments were conducted on daily drug demand

data from Dr. Tadjuddin Chalid Hospital Makassar

for the period of 2023-2024. The dataset included

more than 100 types of drugs. The first step is data

preprocessing (data cleaning, differencing, and

normalization), followed by extracting demand

pattern features and seasonal features. Demand

patterns were classified into the following categories:

a.The smooth Demand has a normal pattern, b.Erratic

Demand is a need with a high quantity of variation, c.

Intermittent Demand is a need with high variation in

the interval between two needs, but has low variation

in quantity needs., d. Lumpy Demand is a need with

high variation in the interval of two needs and

RITECH 2025 - The International Conference on Research and Innovations in Information and Engineering Technology

212

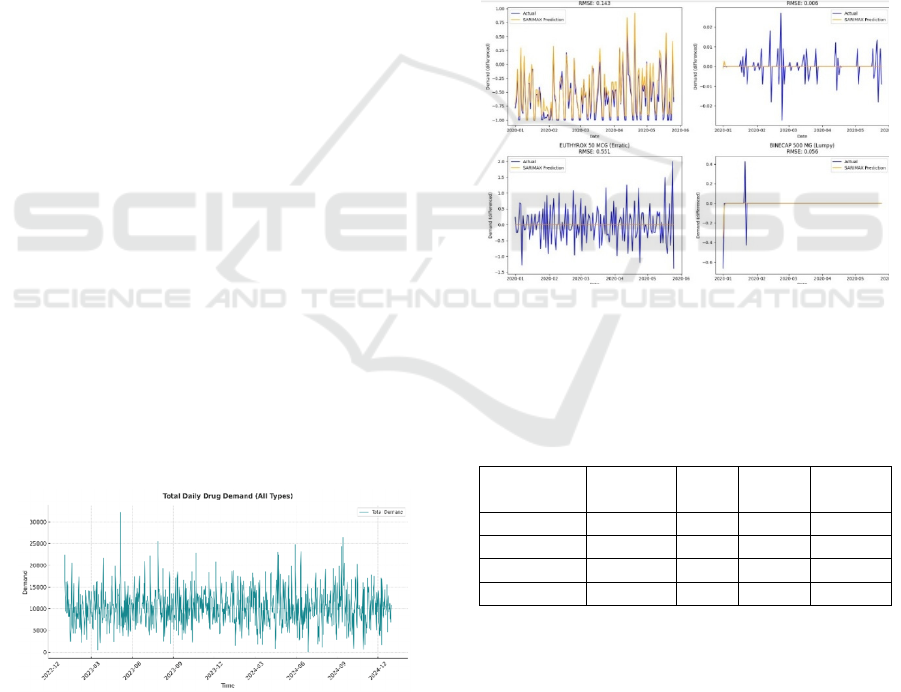
quantity Classification of demand patterns can be

done using 2 classification coefficients, namely the

average demand interval (𝑝) and the square of the

coefficient of variation 𝐶𝑉2. The separation point of

each coefficient is p = 1.32 and 𝐶𝑉2= 0.49.

Extraction results from existing datasets: Smooth

Demand, 90 drugs; intermittent demand, 2 drugs;

erratic demand, 13 drugs; and Lumpy Demand, 6

drugs.

3.1 SARIMAX Model

We performed SARIMAX modeling on the drug data

using Python on Google Collab. Figure 1. shows drug

usage data from Dr. Tadjuddin Chalid Hospital

Makassar from 2023 to 2025. A general upward trend

is observed from 2023 to 2024. This indicates that the

need for drugs tends to increase over time. Although

there are fluctuations, the increase in total demand is

more consistent in 2024 than in the early 2023. The

demand pattern fluctuated sharply on a periodic basis

(rising and falling sharply every few days). This is

most likely due to weekly or monthly ordering

behavior, as well as healthcare activity (e.g., spikes at

the beginning of the working week). The amplitude

of the fluctuations was quite large, indicating high

volatility in drug demand. Some extreme

spikes/outliers (> 30,000) were observed, particularly

in early and mid-2023. For SARIMAX modeling,

AutoArima was used to automatically select the best

parameters for the SARIMAX model based on

historical data. Autoarima used a grid search

approach to try various combinations of parameters

(P, D, Q) and (P,D,Q,m) to find a model with the

smallest Akaike Information Criterion (AIC) or

Bayesian Information Criterion (BIC) values. The

smaller the AIC/BIC ratio, the better the model

explains the data without overfitting.

Figure 1: The Original Time Series.

Based on Figure 2., the sarimax model works quite

well for drugs in the smooth category. The demand is

quite regular, and fluctuations are small, and the

Sarimax predictions are quite accurate, following the

actual pattern well, and RMSE: 0.143 is quite low,

indicating a good prediction. However, for the other

three categories, the SARIMAX model does not work

sufficiently well. Intermittedly, many values are zero

or very small, with random spikes. The graph is

almost always flat (straight line at zero) and the model

fails to capture small and sporadic spikes in demand.

RMSE: 0.006 appears low, but this can be misleading,

as the model only estimates the mean of zero. For

large and irregular Erratic Fluctuations, SARIMAX

Prediction: Unable to keep up with sharp spikes and

dips; RMSE: 0.551–the highest among all, indicating

poor prediction performance. On Lumpy, almost

always zero, with occasional large spikes. SARIMAX

Prediction: Straight line close to zero cannot capture

occasional demands. The RMSE of 0.056 is low, but

the model clearly does not capture surge dynamics.

Figure 2: SARIMAX Model based on Drug Category.

The following are the results of the RMSE

evaluation of the SARIMAX model based on the drug

category.

Table 1: RMSE Evaluation SARIMAX Model.

Demand

Type

Amount of

drug

Min

RMSE

Max

RMSE

Avg

RSME

Smooth 90 0.000 1.037 0.240

Intermittent 2 0.006 0.047 0.026

Erratic 13 0.078 0.735 0.477

Lumpy 6 0.000 0.611 0.180

Based on Table 1., the Smooth Demand with a

total of 90 types of drugs, with an average RMSE of

0.240, is quite low for a statistical model. This

indicates that SARIMAX is suitable for stable

demand and exhibits a clear seasonal pattern or trend.

In the Intermittent Demand category for the two

drugs, the Average RMSE of 0.026 was very low.

However, the number of drugs was too small (n = 2);

therefore, this result is not representative. For the

A Hybrid SARIMAX-SVR Model for Drug Demand Prediction

213

Erratic Demand with 13 drugs, the highest RMSE was

0.735, and the average RMSE was 0.477, which was

the worst compared to the others. This shows that it is

very difficult to handle erratic patterns because

fluctuations cannot be captured using a

linear/seasonal approach. This supports the need for

hybrid or nonlinear models such as SVR. The average

RMSE was 0.180, which is quite good. However, the

range of RMSE is very wide (0.000–0.611), which

means that some cases can be predicted well (perhaps

due to seasonal patterns), but others fail, perhaps due

to sparsity/volatility. SARIMAX has an inconsistent

performance for this type of demand.

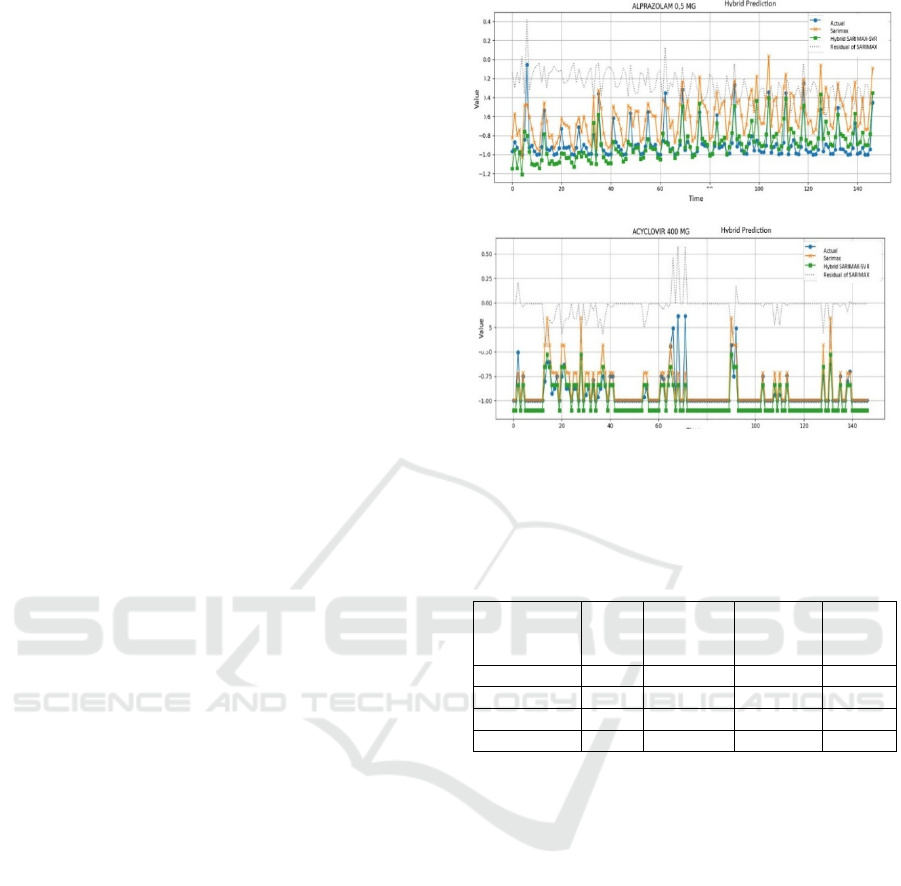
3.2 Hybrid Model with SVR

The SVR model uses residual data from the

SARIMAX model to identify nonlinear patterns. In

Figure 3a. SARIMAX predictions appear volatile and

tend to overreact to short-term fluctuations. The

model often overestimates values, particularly when

the actual demand is stable or low, and fails to capture

the long-term stability observed in the data. The

residuals display a repetitive pattern, indicating that

the model does not fully capture the underlying

dynamics and that additional nonlinear information

remains unexplained. By contrast, the hybrid

SARIMAX–SVR model produces predictions that

are consistently closer to the actual values, more

stable against minor noise, and less prone to extreme

deviations. The ability of the hybrid to maintain

consistency when the actual data tends to be low and

stable is a major advantage.

Likewise, in Figure 3b, SARIMAX is able to

follow certain spikes but performs poorly in periods

with zero demand or sudden fluctuations, leading to

large deviations from the actual values. Again, the

residuals reveal structured patterns, suggesting

incomplete modeling of the series. The hybrid model

demonstrates improved flexibility by reducing errors

at both spikes and low-value regions, producing

predictions that are generally more aligned with the

observed demand. The following are the RMSE

evaluation results for the hybrid model (SVR

correction based on residual data):

(a)

(b)

Figure 3: Comparison of SARIMAX vs Hybrid

SARIMAX-SVR predictions for selected drug: (a)

Alprazolam 0.5 mg), (b) Acyclovir 400 mg.

Table 2: RMSE Evaluation SARIMAX and SVR Model

Hybrid.

Demand Type

Amount

of drug

Avg RMSE

SARIMAX

Avg RMSE

SVR

Avg

RMSE

Hybri

Smooth 90 0.239957 0.115559 0.115559

Intermittent 2 0.026251 0.050815 0.050815

Erratic 13 0.476634 0.368423 0.368423

Lum

6 0.179767 0.166393 0.166393

Based on Table 2., for Smooth Demand (90

drugs), the average RMSE dropped to 0.115 from

0.240 in SARIMAX. A decrease of more than 50%

shows that the hybrid model improved the prediction

accuracy for stable patterns. Min RMSE = 0,

indicating that some predictions are precise.

Intermittent Demand (2 drugs), RMSE decreased to

0.0508 from 0.026 in SARIMAX, but the amount of

data is so small that even small fluctuations can have

a significant effect. Max RMSE is still low (<0.1),

meaning the prediction is still accurate in general.

Erratic Demand (13 drugs), the average RMSE

dropped from 0.477 to 0.360, showing significant

improvement. However, the RMSE value was still

quite high, indicating that erratic patterns remained

difficult to predict. The hybrid model is helpful but

not optimal, and there may be a need for a more

adaptive model. Lumpy Demand (six drugs), the

average RMSE dropped from 0.180 to 0.166, a small

but statistically significant improvement. Max RMSE

RITECH 2025 - The International Conference on Research and Innovations in Information and Engineering Technology

214

dropped slightly from 0.611 to 0.503, hybrid model

more stable at extremes.

Compared to other hybrid models such as

SARIMAX–LSTM or SARIMA–XGBoost reported

in previous studies [5–7], the SARIMAX–SVR offers

shorter training times (<7s per drug) with competitive

accuracy (44% RMSE reduction), making it more

practical for hospital forecasting systems.

Table 3: RMSE Comparison of SARIMAX and Hybrid

SARIMAX -SVR.

Drug Name RMSE

SARIMAX

RMSE

Hybri

Improvement

Thyrozo 5

1.000000 0.000000 1.000000

INH 100

1.005824 0.104220 0.901604

Depakote

ER 250 MG

0.984608 0.116687 0.867922

The comparison of RMSE for SARIMAX and

Hybrid SARIMAX - SVR for several drugs is as

shown in Table 3. Based on the Table 3, these three

drugs showed a drastic performance improvement of

> 86%–100%. This is a strong indicator that

SARIMAX residuals contain hidden patterns can be

modelled by SVR. The hybrid model (SARIMAX +

SVR) consistently outperforms SARIMAX,

especially for: Drugs with irregular demand patterns

and those that may exhibit lumpy or erratic

characteristics. [

3.3 Comparative Context

The hybrid SARIMAX–SVR model demonstrated

superior performance compared to the single

SARIMAX model, achieving an average RMSE

reduction of approximately 44% across different drug

demand categories. This improvement aligns with the

results of Zhao and Zhang (2023), who reported a

38% error reduction in hybrid influenza forecasts, and

Man et al. (2023), whose SARIMA–XGBoost model

reduced RMSE by over 25% in epidemiological

prediction.

Compared with deep-learning-based hybrids such

as SARIMAX–LSTM (Benitez et al., 2023) or

SARIMA–XGBoost (Man et al., 2023), the proposed

SARIMAX–SVR model offers competitive accuracy

while maintaining computational efficiency—

training and prediction completed in under seven

seconds per drug. This advantage is particularly

relevant in hospital environments, where rapid and

scalable forecasting is essential.

Moreover, the integration of SVR effectively

corrected nonlinear residuals, stabilizing predictions

in erratic and lumpy demand categories. These

findings are consistent with Liu and Han (2023) and

Li and Zhao (2024), who emphasized the importance

of residual-based learning in improving hybrid time-

series robustness. Thus, the SARIMAX–SVR model

not only refines prediction accuracy but also offers

practical feasibility for routine pharmaceutical

demand management.

4 CONCLUSIONS

This study proposes a drug demand prediction

approach based on the SARIMAX–SVR hybrid

model to improve the accuracy of drug demand

forecasting in JKN services. Based on the evaluation

of drug supply data from Dr. Tadjuddin Chalid

Makassar Hospital, the hybrid model demonstrated

superior predictive performance compared to the

single approach, with an average RMSE reduction of

approximately 44% across various drug demand

categories.The SARIMAX model is effective in

capturing linear and seasonal patterns, whereas SVR

can correct nonlinear and fluctuating prediction

errors. The integration of the two enables a more

adaptive, accurate, and suitable prediction system to

support informed decision making in hospital

pharmacy logistics management. This study was

limited to data from a single hospital; future research

should expand to multiple hospitals across different

regions of Indonesia to improve generalizability

within the JKN system

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Tadjuddin Chalid

Makassar Hospital, for providing access to the drug

datasets essential to this research.(Fan et al., 2022),(A

et al., 2025)(Aravazhi, 2021)

REFERENCES

A, S., Christo, M. S., & Elizabeth, J. V. (2025). A hybrid

approach to time series forecasting: Integrating

ARIMA and prophet for improved accuracy. Results in

Engineering, 27(June), 105703.

https://doi.org/10.1016/j.rineng.2025.105703

Alharbi, F. R., & Csala, D. (2022). A Seasonal

Autoregressive Integrated Moving Average with

Exogenous Factors (SARIMAX) Forecasting Model-

Based Time Series Approach. Inventions, 7(4).

https://doi.org/10.3390/inventions7040094

A Hybrid SARIMAX-SVR Model for Drug Demand Prediction

215

Alsaber, A. R., Al-Herz, A., Alawadhi, B., Doush, I. A.,

Setiya, P., AL-Sultan, A. T., Saleh, K., Al-Awadhi, A.,

Hasan, E., Al-Kandari, W., Mokaddem, K., Ghanem,

A. A., Attia, Y., Hussain, M., AlHadhood, N., Ali, Y.,

Tarakmeh, H., Aldabie, G., AlKadi, A., & Alhajeri, H.

(2024). Machine learning-based remission prediction in

rheumatoid arthritis patients treated with biologic

disease-modifying anti-rheumatic drugs: findings from

the Kuwait rheumatic disease registry. Frontiers in Big

Data, 7. https://doi.org/10.3389/fdata.2024.1406365

Alzami, F., Salam, A., Rizqa, I., Irawan, C., Andono, P. N.,

Aqmala, D., & Sartika, M. (2024). Demand Prediction

for Food and Beverage SMEs Using SARIMAX and

Weather Data. Ingenierie Des Systemes d’Information,

29(1), 293–300. https://doi.org/10.18280/isi.290129

Aravazhi, A. (2021). Hybrid Machine Learning Models for

Forecasting Surgical Case Volumes at a Hospital. AI

(Switzerland), 2(4), 512–526.

https://doi.org/10.3390/ai2040032

Ashtar, D., Mohammadi Ziabari, S. S., & Alsahag, A. M.

M. (2025). Hybrid Forecasting for Sustainable

Electricity Demand in The Netherlands Using

SARIMAX, SARIMAX-LSTM, and Sequence-to-

Sequence Deep Learning Models. Sustainability

(Switzerland), 17(16).

https://doi.org/10.3390/su17167192

Benitez, I. B., Ibañez, J. A., Lumabad, C. I. I. I. D., Cañete,

J. M., & Principe, J. A. (2023). Day-Ahead Hourly

Solar Photovoltaic Output Forecasting Using

SARIMAX, Long Short-Term Memory, and Extreme

Gradient Boosting: Case of the Philippines.

Energies_MDPI, 16.

https://doi.org/10.3390/en16237823

Fan, B., Peng, J., Guo, H., Gu, H., Xu, K., & Wu, T. (2022).

Accurate Forecasting of Emergency Department

Arrivals With Internet Search Index and Machine

Learning Models: Model Development and

Performance Evaluation. JMIR Medical Informatics,

10(7), 1–17. https://doi.org/10.2196/34504

Lee, J., Cho, Y., Lee, J., & Ph, D. (n.d.). National - scale

electricity peak load forecasting : Traditional , machine

learning , or hybrid model ? National - scale electricity

peak load forecasting : Traditional , machine learning

, or hybrid model ? 1–42.

Man, H., Huang, H., Qin, Z., & Li, Z. (2023). Analysis of a

SARIMA-XGBoost model for hand, foot, and mouth

disease in Xinjiang, China. Epidemiology and Infection,

151. https://doi.org/10.1017/S0950268823001905

Pankratz.A. (2019). Forecasting with Unvariate Box-

Jenkins Model Concept and Cases. In John Wily &

Sons,Inc. Indiana (Vol. 11, Issue 1).

http://scioteca.caf.com/bitstream/handle/123456789/10

91/RED2017-Eng-

8ene.pdf?sequence=12&isAllowed=y%0Ahttp://dx.do

i.org/10.1016/j.regsciurbeco.2008.06.005%0Ahttps://

www.researchgate.net/publication/305320484_SISTE

M_PEMBETUNGAN_TERPUSAT_STRATEGI_ME

LESTARI

Satibi, S., Copalcanty, F. A., Tuko, E., & Sawatiandari, L.

G. (2020). Pharmaceutical suply chain management in

supporting drugs avaibility in the jkn era in indonesia.

International Journal of Scientific and Technology

Research, 9(4), 3034–3038.

Teja, M. D., & Rayalu, G. M. (2025). Hybrid time series

and machine learning models for forecasting

cardiovascular mortality in India: an age specific

analysis. BMC Public Health, 25(1).

https://doi.org/10.1186/s12889-025-23318-7

Yulianti, R., Amanda, N. T., Notodiputro, K. A., Angraini,

Y., & Mualifah, L. N. A. (2025). Comparison of Sarima

and Sarimax Methods for Forecasting Harvested Dry

Grain Prices in Indonesia. Barekeng, 19(1), 319–330.

https://doi.org/10.30598/barekengvol19iss1pp319-330

Zhao, D., & Zhang, R. (2023). A new hybrid model

SARIMA-ETS-SVR for seasonal influenza incidence

prediction in mainland China. Journal of Infection in

Developing Countries, 17(11), 1581–1590.

https://doi.org/10.3855/jidc.18037

RITECH 2025 - The International Conference on Research and Innovations in Information and Engineering Technology

216