Witness Byzantine Fault Tolerance with Signature Tree and

Proof-of-Navigation for Wide Area Visual Navigation

Nasim Paykari

1 a

, Taylor Clark

, Ademi Zain

, Damian Lyons

1 b

and Mohamed Rahouti

2 c

Computer and Information Science Department, Fordham University, Bronx, NY 10458, U.S.A.

Computer and Information Science Department, Fordham University, New York, NY 10023, U.S.A.

Keywords:

Blockchain, Byzantine Fault Tolerance, Multi-Signature, Merkle Tree, Wide Area Visual Navigation,

Cooperative Robotics.

Abstract:

This paper presents Witness Byzantine Fault Tolerance (WBFT), a novel consensus protocol designed for Wide

Area Visual Navigation (WAVN) systems, where cooperative robots share visual imagery in GPS-denied en-

vironments and reach agreement on navigation data via blockchain. WBFT addresses the limitations of tradi-

tional Byzantine Fault Tolerance (BFT) methods, particularly the high communication overhead of protocols

like PBFT, by introducing a lightweight, secure, and signature-based consensus mechanism optimized for

resource-constrained robotic networks. The protocol integrates a Proof-of-Stake-based leader election system,

named Proof-of-Navigation (PoN), with a signature aggregation approach using Ed25519 cryptography and

a Merkle tree structure, reducing veriﬁcation complexity to O(logt) and achieving consensus with only O(n)

message complexity. WBFT tolerates up to f ≤ ⌊(n − 1)/3⌋ Byzantine faults and demonstrates superior re-

silience, scalability, and communication efﬁciency compared to existing BFT variants. Experimental results

validate WBFT’s performance across multiple metrics and network sizes, conﬁrming its suitability for high-

frequency, decentralized robotic coordination.

1 INTRODUCTION

Wide Area Visual Navigation (WAVN) enables a

group of robots to collaboratively navigate by shar-

ing visual imagery, assisting a robot in locating a des-

ignated home through a sequence of common land-

marks (Lyons and Rahouti, 2023). WAVN integrates

a blockchain where robots earn tokens for sharing im-

agery among other activities, and the robot with the

most tokens wins the right to generate the next block

(Paykari et al., 2024). However, faulty or malicious

robots can disrupt consensus, risking the integrity of

the blockchain and navigation process. In contrast,

traditional consensus protocols like Practical Byzan-

tine Fault Tolerance (PBFT) suffer from high message

complexity and limited trust in an open network, im-

practical for open or resource-constrained networks

(Castro et al., 1999).

To address this, we introduce the Witness Byzan-

tine Fault Tolerance (WBFT) protocol, a consensus

https://orcid.org/0009-0005-6793-7417

https://orcid.org/0000-0003-1460-9741

https://orcid.org/0000-0001-9701-5505

mechanism tailored to combine with the main con-

sensus of WAVN’s Blockchain. The WBFT protocol

is designed to meet the needs of the WAVN system,

where robots must reach consensus on navigation data

while tolerating Byzantine faults. The protocol lever-

ages a selected leader through the PoN phase and

threshold signatures to optimize performance. WBFT

leverages a multi-signatures with aggregation to min-

imize communication overhead, achieving consen-

sus in two rounds (propose and witness/committed)

with O(n) message complexity and tolerating up to

( f ≤ ⌊(n−1)/3⌋) Byzantine faults. Unlike traditional

PBFT (Castro et al., 1999), WBFT uses a predeﬁned

leader and aggregated signatures to reduce network

trafﬁc, making it suitable for resource-constrained

robots.

The WBFT Byzantine fault tolerance method in-

tegrates a digital signature-based strategy to achieve

consensus in a distributed network, improving the tra-

ditional voting mechanisms. In each consensus round,

the designated leader, determined by a precomputed

schedule in the Robostake component (Paykari et al.,

2024), broadcasts a message to all nodes in the net-

work. This message is accompanied by the leader’s

Paykari, N., Clark, T., Zain, A., Lyons, D. and Rahouti, M.

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation.

DOI: 10.5220/0013961300003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 633-644

ISBN: 978-989-758-770-2; ISSN: 2184-2809

633

digital signature, which allows each node to inde-

pendently verify both the message’s validity and the

leader’s identity using a predeﬁned cryptographic

scheme.

Upon receiving the message, a node validates the

leader’s signature and the message content. If valid,

the node appends its own digital signature to the mes-

sage, acting as a witness to both the message’s cor-

rectness and the leader’s signature. This doubly-

signed message is then rebroadcast to the network.

Upon receiving a message with two signatures, sub-

sequent nodes verify both signatures. If the signatures

are valid, the node replaces the second signature with

its own and rebroadcasts the message. This process

creates a chain of signature updates, where each node

contributes to the message’s validation.

To ensure scalability and efﬁciency, nodes orga-

nize signatures into a Merkle tree structure, with in-

dividual signatures forming the leaves. As signa-

tures accumulate, the Merkle tree is updated, allow-

ing nodes to track the number of valid signatures ef-

ﬁciently. Once the number of signatures surpasses a

predeﬁned threshold, the message is considered com-

mitted and eligible for inclusion in the blockchain.

The committed message and its Merkle tree are then

broadcast to the network for ﬁnal inclusion in the

blockchain.

This method leverages the Robostake component

to precompute the leader for each block, ensuring de-

terministic leader selection and reducing the risk of

leader-based attacks. The approach mitigates various

Byzantine faults, including malicious leader behavior,

by replacing voting with a signature-based validation

and propagation mechanism. It enhances resilience

against other attack vectors, such as Sybil attacks and

message tampering.

The key contributions of this paper are summa-

rized as follows.

• Propose WBFT, a novel consensus protocol

tailored for WAVN in GPS-denied, resource-

constrained robotic environments.

• Introduce a Proof-of-Navigation (PoN) mecha-

nism, a PoS-inspired leader selection algorithm

based on robots’ navigation reliability and envi-

ronmental adaptability, ensuring transparent and

tamper-proof leader election.

• Leverage a Merkle tree–based multi-signature ag-

gregation method that reduces veriﬁcation com-

plexity from O(n) to O(logt), enabling efﬁcient

consensus validation among robotic agents.

• Achieve consensus in only two rounds (pro-

pose and witness) with O(n) message complex-

ity, signiﬁcantly reducing communication over-

head compared to classical PBFT and its variants.

• Demonstrate that WBFT tolerates up to f ≤ ⌊(n −

1)/3⌋ Byzantine nodes and ensures correctness

and liveness in adversarial network settings.

• Provide comprehensive experimental benchmarks

comparing WBFT to BLS, aggregate, and thresh-

old signature schemes, and evaluate scalability

across varying network sizes.

• Validate WBFT’s suitability for high-frequency,

decentralized robotic coordination tasks in visual

navigation, particularly under bandwidth and re-

source constraints.

The rest of this paper is structured as follows. Sec-

tion 2 provides background on the WAVN system,

blockchain integration, and the hybrid PoS–BFT con-

sensus mechanism. Section 3 reviews relevant work

in Byzantine fault tolerance and consensus protocols.

Section 4 details the design of the WBFT protocol,

including its cryptographic components and signature

aggregation scheme. Section 5 presents experimental

results evaluating performance and scalability. Sec-

tion 6 discusses key insights and limitations, and Sec-

tion 7 concludes the paper with directions for future

work.

2 BACKGROUND AND SYSTEM

CONTEXT

To better understand the design rationale behind the

proposed protocol, this section presents the key com-

ponents and operational context of the WAVN sys-

tem. It outlines the role of collaborative visual local-

ization, blockchain-based incentives, and the hybrid

consensus mechanism that combines PoS leader se-

lection with Byzantine fault tolerance. These founda-

tional concepts establish the system requirements and

assumptions guiding our methodological design.

2.1 Wide Area Visual Navigation

(WAVN)

In WAVN, a group of robots collaborates to guide

a robot in a dynamic and GPS-denied environment

to a designated location using shared visual imagery.

Each robot captures and shares images of its sur-

roundings. Any robot in the team that needs to navi-

gate to a location, identiﬁed by a goal image, out of its

immediate ﬁeld of view, leverages the imagery from

the team to ﬁnd a sequence of landmarks seen in com-

mon between team members that can be followed to

the target location.

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

634

2.2 Blockchain

Robots generate transactions that include imagery of

the main robot and common landmarks between it and

another robot. In the next level, robots compete to

generate the next block, which leads to the reward of

a constant amount of tokens. The system incentivizes

participation through a blockchain where:

• Robots earn tokens for activities such as contribut-

ing valid imagery and common landmarks, partic-

ipating in the network, or generating a block.

• A competition process, as described in (Paykari

et al., 2025a), determines the next block generator

based on token accumulation.

• The blockchain records imagery and common

landmarks contributions, ensuring transparency,

immutability, and accessibility.

• In case of navigation needs, a robot uses the ledger

and retrieves transactions to generate a sequence

of common landmarks from the current position

to the home (Paykari et al., 2025b).

2.3 Hybrid Consensus

Whether silent (failing to respond) or Byzantine

(sending malicious data), Faulty robots can disrupt

navigation or manipulate records. Consensus ad-

dresses this by securing the blockchain, ensuring only

valid imagery contributions are recorded.

2.3.1 PoS Based Consensus

The PoN system, as outlined in (Paykari et al., 2024;

Paykari et al., 2025a), employs a blockchain-based

Proof-of-Stake (PoS) mechanism to select a leader for

cooperative navigation among robotic teams. Each

robot is assigned a stake through a stake weight func-

tion, which evaluates its navigation reliability based

on factors like historical performance. A PoS con-

sensus score is then calculated, reﬂecting each robot’s

inﬂuence, with higher scores indicating greater trust-

worthiness. The robot with the highest consensus

score is dynamically chosen as the leader for a given

block, coordinating tasks like path planning using

veriﬁed data stored on the blockchain. This en-

sures transparent, tamper-proof selection. A navi-

gability function further tailors the stake to the spe-

ciﬁc environment, providing the leader is best suited

for tasks like navigating agricultural ﬁelds or dense

forestry. The system adapts dynamically, reassigning

leadership as conditions or robot performance change,

though challenges like faulty leaders or Byzantine be-

havior remain unsolved.

The leader selection process for the robotic team

is managed through the PoS-based PoN mechanism,

which is tailored for cooperative navigation Alg. 1. It

works in this way:

1. Stake Weight Function:

• Each robot in the team is assigned a stake

based on its navigation reliability and activi-

ties. This reliability is determined by factors

such as historical performance or contribution

to the team’s navigation goals.

• The stake weight function quantiﬁes the por-

tion of the stake by the robot compared to the

whole stake, giving a higher chance to robots

with more reliable navigational sharing to be

selected as the next leader.

2. PoS Consensus Score:

• The PoN system calculates a consensus score

for each robot based on its stake. This score

reﬂects the robot’s inﬂuence in the decision-

making process.

• Robots with higher consensus scores (i.e., those

with higher stakes due to reliable navigation

data) are prioritized for leadership roles.

3. Leader Selection:

• The robot with the highest consensus score at

a given time is selected as the leader for the

next block generation. The leader is responsi-

ble for collecting transactions and broadcasting

them as a new block that, along with the collec-

tive data veriﬁed through the blockchain, will

be used for path planning.

• The blockchain ensures that the selection pro-

cess is transparent and tamper-proof, as all

robots validate the leader’s score using the de-

centralized ledger and the last block.

4. Dynamic Updates:

• The leader role is not ﬁxed; it can change dy-

namically as the robots’ stakes and consensus

scores are updated based on real-time perfor-

mance and environmental conditions.

• For example, if a robot’s sensors degrade or its

navigation data becomes less reliable, its stake

and consensus score decrease, reducing its like-

lihood of being selected as the leader. Even if

a robot becomes isolated from others, it has no

chance of becoming the next leader.

2.3.2 Byzantine Fault Tolerance

To ensure the integrity and reliability of the WAVN

blockchain in the presence of faulty or malicious

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation

635

robots, the WBFT protocol is integrated with the

PoN’s Proof-of-Stake (PoS) mechanism to achieve ro-

bust consensus. WBFT addresses Byzantine faults,

such as robots sending malicious imagery or manip-

ulating navigation data, by leveraging a signature-

based consensus mechanism that eliminates the high

message complexity of traditional PBFT. Unlike

PBFT’s, WBFT achieves agreement through a two-

phase process (propose and witness) using aggregated

Ed25519 signatures and a Merkle tree structure. In

the propose phase, the leader, selected via the PoN

process based on its consensus score, broadcasts a

block containing imagery transactions with its digi-

tal signature. Nodes validate this signature and con-

tribute their own signatures to a Merkle tree, where

each signature is hashed with the node’s identiﬁer

to form a leaf, enabling efﬁcient veriﬁcation with

O(logt) complexity for a threshold t = ⌊2n/3⌋ + 1.

This approach tolerates up to f ≤ ⌊(n − 1)/3⌋ Byzan-

tine faults.

In the witness phase, once the threshold number of

valid signatures is collected, the Merkle tree’s root is

broadcast, allowing all nodes to verify the block’s au-

thenticity and the threshold condition independently.

The use of Ed25519 signatures ensures fast signing

and veriﬁcation, with compact 32-byte public keys

and 64-byte signatures, minimizing network over-

head, critical for robots sharing high-frequency vi-

sual imagery. The protocol’s integration with PoN

ensures that only reliable robots with high consensus

scores lead the consensus, reducing the risk of mali-

cious leader behavior.

3 STATE-OF-THE-ART

Blockchain technology has emerged as a powerful

tool for enabling decentralized trust in robotics and

navigation systems (Aditya et al., 2021), particularly

in applications like WAVN (Paykari et al., 2024). The

PBFT protocol, a cornerstone of BFT, achieves con-

sensus in partially synchronous networks but incurs

high communication overhead with O(n

) messages

due to its all-to-all communication in the prepare and

commit phases (Castro et al., 1999). Recent BFT vari-

ants, such as HotStuff and Tendermint, improve scal-

ability by reducing message complexity and optimiz-

ing leader rotation. Yet, they still struggle in resource-

constrained environments due to computational de-

mands (Yang and Bajwa, 2019). Threshold signa-

ture schemes, like BLS, provide compact signatures

but require complex setup phases, which can be im-

practical for dynamic robotic networks (Boneh et al.,

2018). In contrast, our WBFT protocol leverages

a lightweight, signature-based consensus mechanism

with aggregated Ed25519 signatures and a Merkle

tree structure, achieving O(n) message complexity

and eliminating the need for complex setup, making

it ideal for bandwidth-constrained robotic systems.

BFT remains critical for ensuring reliable consen-

sus in distributed systems despite malicious or faulty

nodes, with recent advancements enhancing scala-

bility and adaptability for modern applications like

blockchain and cyber-physical systems (CPS). Liu

and Junwu (Liu and Zhu, 2024) propose AP-PBFT.

This enhanced PBFT framework incorporates a Ver-

iﬁable Random Function (VRF) to select consensus

and primary nodes, ensuring fair proposal aggrega-

tion for multi-value consensus in decentralized au-

tonomous organizations (DAOs). An incentive mech-

anism promotes honest participation, reducing col-

lusion risks and improving efﬁciency in complex

decision-making scenarios. Unlike AP-PBFT’s focus

on multi-value consensus and incentive-driven partic-

ipation, WBFT prioritizes a streamlined, signature-

based approach using a Merkle tree to achieve efﬁ-

cient veriﬁcation with O(logt) complexity, tailored

for resource-constrained robotic networks in WAVN.

Wang et al. (Huang et al., 2022) introduce

WRBFT, a PBFT variant that uses workload-based

node selection and VRF for dynamic primary node as-

signment, addressing ﬁxed node roles and high com-

munication overhead. By enabling ﬂexible node entry

and exit, WRBFT enhances scalability and resilience,

making it suitable for large-scale blockchain net-

works. WBFT diverges by integrating a precomputed

leader schedule via the PoS-inspired PoN mechanism

and employing aggregated Ed25519 signatures, re-

ducing communication overhead and optimizing per-

formance for robotic systems with limited bandwidth.

Wu et al. (Wu et al., 2023) develop RPBFT, tai-

lored for CPS, with improved master node election,

robust malicious node detection, and optimized view

changes to reduce communication delays and increase

throughput. This method ensures reliable consensus

in resource-constrained IoT-enabled blockchain sys-

tems while maintaining security against Byzantine

faults. In contrast, WBFT uses a Merkle tree-based

signature aggregation to achieve efﬁcient veriﬁcation

and incorporates a leader rotation mechanism, mak-

ing it more suitable for high-frequency, bandwidth-

constrained robotic navigation tasks in WAVN.

Byzantine-resilient Distributed Coordinate De-

scent (ByRDiE) (Yang and Bajwa, 2019) tack-

les Byzantine faults in high-dimensional distributed

learning, enabling robust optimization in decentral-

ized machine learning tasks across convex and non-

convex settings. Its focus on data-driven applica-

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

636

tions expands BFT’s scope beyond blockchain, of-

fering resilience in adversarial environments. WBFT,

however, is explicitly designed for blockchain-based

robotic navigation, using a signature tree method to

ensure efﬁcient consensus with O(logt) veriﬁcation

complexity, distinct from ByRDiE’s optimization-

centric approach.

Asynchronous Algorand (Abraham et al., 2025)

advances BFT for blockchain systems by achieving

near-linear communication complexity and constant

expected time, even in dynamic networks with un-

known participation. Its asynchronous design over-

comes limitations of synchronous BFT protocols in

handling network delays and partitions, enhancing

scalability. Unlike Asynchronous Algorand’s fo-

cus on asynchronous consensus, WBFT employs a

synchronous, signature-based mechanism optimized

for deterministic leader selection and compact signa-

ture aggregation, prioritizing efﬁciency in resource-

constrained robotic environments.

The reviewed methods, AP-PBFT, WRBFT,

RPBFT, ByRDiE, and Asynchronous Algorand,

demonstrate signiﬁcant strides in addressing scala-

bility, efﬁciency, and adaptability in BFT protocols

across diverse applications. WBFT distinguishes it-

self by combining a signature-based consensus with

a Merkle tree structure and PoS-based PoN leader se-

lection, achieving low communication overhead, tai-

lored for WAVN’s robotic blockchain system.

Algorithm 1: PoN leader selection.

Data: Set of robots R = {r

,...,r

} with

navigation histories and performance

metrics

Result: Selected leader r

∗

for the next block

generation

foreach r

∈ R do

Retrieve navigation reliability score s

based on last committed block (B

n−1

);

Compute stake weight w

∑

j=1

;

Compute PoS consensus score

= f (w

,navigability context);

Select robot r

∗

with the highest consensus

score c

;

if multiple robots share max c

then

Break tie using secondary metrics (e.g.,

recency of successful navigation or

token age);

return r

∗

as the PoN leader for the current

round;

4 METHODOLOGY

This section details the methodology and structure of

the WBFT protocol, providing a comprehensive ex-

planation of its components and their roles in achiev-

ing consensus in a distributed system. Each compo-

nent of WBFT is justiﬁed with respect to its contri-

bution to fault tolerance, security, and efﬁciency. Ad-

ditionally, we highlight that multiple solutions exist

for each component of the protocol, and by substitut-

ing or reﬁning these modular elements, the method’s

performance, scalability, or resilience may be further

improved.

4.1 Signatures and Veriﬁcations

To ensure secure and efﬁcient message valida-

tion in the WBFT protocol, we evaluate three

cryptographic methods, including ECDSA-secp256r1

(Kramer et al., 2018), Ed25519 (Bisheh-Niasar et al.,

2021), and RSA-2048-bit (Sadikin and Wardhani,

2016) for generating public/private key pairs, creat-

ing digital signatures, and verifying them across a

distributed network. These methods are compared

based on signing time, veriﬁcation time, and the sizes

of public keys, private keys, and signatures, as these

metrics directly impact the protocol’s performance

and network overhead. Keys and signatures are seri-

alized using the DER format for ECDSA and RSA,

and raw encoding for Ed25519, ensuring compati-

bility with network transmission requirements. The

evaluation reveals Ed25519 offers the fastest sign-

ing and veriﬁcation with compact key and signa-

ture sizes, ideal for bandwidth-constrained networks;

ECDSA provides a balanced approach with moderate

sizes and performance; and RSA, while secure, incurs

higher computational and size overheads. By analyz-

ing these metrics, we identify Ed25519 as a promising

candidate for WBFT, with the ﬂexibility to adopt al-

ternative methods based on speciﬁc security or perfor-

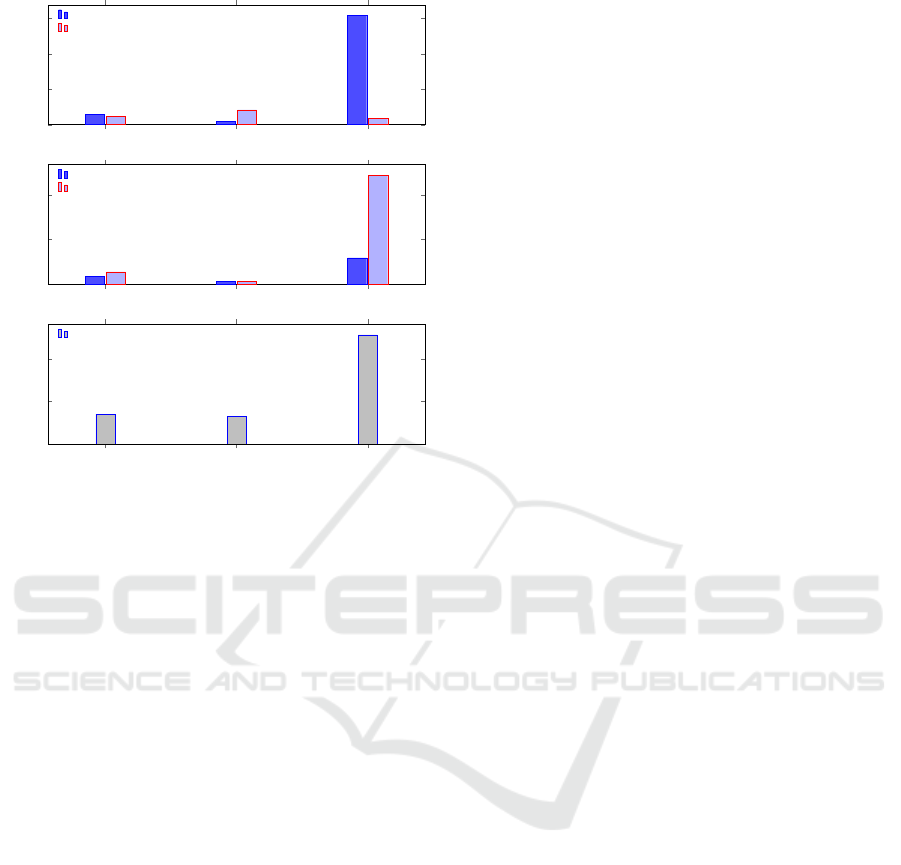
mance needs. The results are visualized in Figure 1,

highlighting the suitability of each technique for scal-

able Byzantine fault tolerance.

The WBFT protocol employs the DER format for

serializing and deserializing public and private keys

for ECDSA and RSA and raw encoding for Ed25519

due to their compact binary representations. For in-

stance, Ed25519 public keys are 32 bytes, ECDSA

public keys are approximately 70 bytes in DER for-

mat, and signatures are 64 bytes and approximately

70 bytes, respectively. These compact sizes mini-

mize network overhead, ensuring efﬁcient transmis-

sion and processing in WBFT’s broadcast-heavy con-

sensus mechanism.

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation

637

ECDSA (secp256r1) Ed25519 RSA (2048-bit)

0.5

1.5

0.14

5 · 10

−2

1.54

0.12

0.21

9 · 10

−2

Time (ms)

Signing and Veriﬁcation Times

Sign Time (ms)

Verify Time (ms)

ECDSA (secp256r1) Ed25519 RSA (2048-bit)

500

1,000

294

138

1,216

Size (bytes)

Key Sizes

Public Key Size

Private Key Size

ECDSA (secp256r1) Ed25519 RSA (2048-bit)

100

200

256

Cryptographic Method

Size (bytes)

Signature Size

Figure 1: Comparison of ECDSA (secp256r1), Ed25519,

and RSA (2048-bit) in terms of signing/veriﬁcation times

and key/signature sizes, demonstrating Ed25519’s efﬁ-

ciency.

The Ed25519 signature scheme operates over the

Edwards curve deﬁned by x

+ y

= 1 + dx

over a

ﬁnite ﬁeld F

, where p = 2

255

− 19 and d is a curve-

speciﬁc constant. For a private key k ∈ Z, the public

key is computed as A = [k]B, where B is the curve’s

base point. To sign a message M, the signer computes

a scalar r = H(k, M) (where H is a cryptographic

hash function, typically SHA-512), a point R = [r]B,

and a scalar s = r + H(R,A,M) · k mod ℓ, where ℓ

is the order of the curve’s base point. The signa-

ture is the pair (R,s). Veriﬁcation involves checking

if [s]B = R + [H(R,A, M)]A, ensuring the signature’s

validity without revealing k. This scheme’s compact

32-byte keys and 64-byte signatures, combined with

its fast scalar multiplication, make it a good candidate

for WBFT’s high-frequency signature broadcasts.

4.2 Signature Tree

A digital signature authenticates the origin and in-

tegrity of a message, while a multisignature scheme

enables multiple parties to collaboratively sign a

message, enhancing security in distributed systems

like WBFT. Several multisignature approaches exist,

each with unique trade-offs. The BLS (Boneh-Lynn-

Shacham) scheme, leveraging bilinear pairings on the

BLS12-381 curve, aggregates individual signatures

into a compact 48-byte signature, veriﬁed via a single

pairing operation, though veriﬁcation time scales with

the number of signers (Bacho and Loss, 2022). Ag-

gregate signatures concatenate individual signatures

into a single byte string, simplifying veriﬁcation but

resulting in a signature size that grows linearly with

the number of signers, making it less efﬁcient for

large groups (Bellare and Neven, 2006). Threshold

signature schemes require a minimum number of sig-

natures (t-of-n) to validate a message, offering ﬂexi-

bility in signer participation but necessitating individ-

ual veriﬁcation for each signature, which can be com-

putationally intensive (Chu et al., 2023). To address

these limitations, we propose a signature tree method

that integrates threshold signatures with a Merkle tree

structure, enabling efﬁcient veriﬁcation of multiple

signatures in WBFT.

Our signature tree method enhances threshold sig-

natures for the WBFT protocol by integrating them

with a Merkle tree structure, offering efﬁcient veriﬁ-

cation of multiple signatures in distributed systems.

In this approach, a leader node broadcasts a mes-

sage signed by participating nodes to produce individ-

ual signatures. Each signature, concatenated with the

node’s unique identiﬁer, is hashed to form a leaf in the

Merkle tree. The tree is constructed by pairwise hash-

ing leaves up to a single root, representing the collec-

tive signatures. To validate the message, a node ver-

iﬁes that the Merkle root corresponds to a threshold

number of valid signatures, using the associated pub-

lic keys and Merkle paths. This method reduces ver-

iﬁcation complexity from O(n) to O(log n) for n sig-

natures, as only the root and relevant paths need veri-

ﬁcation, making it highly scalable for large networks.

However, constructing the tree introduces computa-

tional overhead, particularly for dynamic node sets,

which must be balanced against the efﬁciency gains

in veriﬁcation.

The method leverages the cryptographic proper-

ties of Merkle trees to ensure integrity and authen-

ticity in WBFT’s consensus mechanism. Requir-

ing a designated leader’s signature in the tree en-

sures a consistent message origin, while witness sig-

natures provide fault-tolerant agreement. The use of a

threshold ensures robustness and efﬁciency, as each

robot that meets the threshold faster has the proof

for committing and adding the block to the chain.

The compact Merkle root, typically 32 bytes (us-

ing SHA-256), minimizes network overhead during

broadcast, making this approach ideal for WBFT’s

high-frequency, bandwidth-constrained environment.

Compared to BLS and aggregate signatures, the sig-

nature tree method offers a balance of scalability and

ﬂexibility, particularly suited for scenarios where par-

tial veriﬁcation of large signer sets is critical. It also

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

638

eliminates needing a trusted channel or third party to

communicate required keys.

Our multi-signature method is chosen for its com-

patibility with Ed25519, which offers fast signing and

veriﬁcation, ideal for resource-constrained robots.

Unlike BLS signatures, which require a complex

setup phase, our method is straightforward, concate-

nating individual signatures while maintaining veri-

ﬁability. Compared to ring signatures, it provides

stronger accountability, as each signer’s contribution

is explicit. The method aligns with WBFT’s fast path,

reducing bandwidth usage in WAVN’s visual data ex-

changes.

4.3 WBFT Protocol

The WBFT protocol is a consensus mechanism tai-

lored for PoN blockchain systems, enabling a group

of n nodes to agree on a shared block of blockchain

ledger despite the presence of up to f ≤ ⌊(n −

1)/3⌋ faulty nodes, ensuring resilience in dynamic,

resource-constrained environments. WBFT achieves

consensus through three main phases: propose, wit-

ness, and commit, requiring a threshold of t =

⌊2n/3⌋ + 1 valid signatures to validate an entry, bal-

ancing security, scalability, and efﬁciency. In the

propose phase, a designated leader node, selected by

the PoN process (see Algorithm 1), initiates consen-

sus by broadcasting a new entry (block) accompanied

by the Ed25519 cryptographic signature. This sig-

nature ensures the entry’s authenticity and integrity,

allowing nodes to verify the leader’s identity. Dur-

ing the witness phase, participating nodes validate the

leader’s signature against the leader’s public key and,

if valid, contribute their own signatures to a Merkle

tree, where each signature is hashed to form a leaf.

The Merkle tree structure organizes these signatures

hierarchically, pairwise hashing leaves to compute

parent nodes until a single root is derived, enabling

efﬁcient veriﬁcation with O(logt) complexity com-

pared to O(n) for traditional threshold schemes.

Once the threshold number of signatures is col-

lected in the commit phase, the fastest reached broad-

casts the Merkle tree, allowing independent veriﬁ-

cation of the threshold condition for others. Each

node recomputes the Merkle root using the provided

tree and signatures, ensuring the leader’s signature

is included and the threshold is met, before append-

ing the entry to the blockchain. This will eliminate

the need for communication overhead in the commit

phase compared to PBFT. A secure key exchange en-

sures that all nodes share public keys before consen-

sus begins, maintaining network reliability.

Consider a set of n nodes in the WBFT proto-

col, with a designated leader node and a threshold

t ≤ n required for block validation. Let B

be the

Block to be signed, and each node i (for i = 1,.. ., n)

has a private key sk

∈ Z and corresponding public

key pk

= [sk

]G, where G is a generator of an ellip-

tic curve group. The leader node signs B

to pro-

duce a signature σ

= Sign(sk

), where Sign is

the signing function. Each witness node i (for i ̸= L)

signs (B

,σ

) to produce σ

= Sign(sk

,(B

,σ

)).

These signatures will create leaves l

= H(ID||σ

and the leader’s leave also includes the block l

H(ID||B||σ

Algorithm 2: Witness Byzantine Fault Tolerance

(WBFT).

Data: Set N = {r

,...,r

} with PKs

{pk

,..., pk

}, leader r

Result: Committed block B

Propose:

creates B

, σ

← Sign(sk

)

Broadcast (B

,σ

)

Witness:

foreach r

∈ N \ {r

} do

Construct Merkle tree T

Let Σ ← {σ

} ∪ {σ

} (received

signatures)

if ∀σ ∈ Σ, Verify(pk

,σ) then

← H(ID

∥ σ) for each σ ∈ Σ

← H(ID

∥ σ

)

Broadcast (σ

← Sign(sk

,(B

,σ

)))

Commit:

if |L| ≥ ⌊2n/3⌋ + 1 then

R ← Root(T )

Broadcast (R,T )

foreach r

∈ N do

if VerifyMerklePath(R, l

,T ) then

Append B

to chain

return B

For pair signatures σ

,σ

, then p

= H(σ

||σ

) is

computed, where H is a cryptographic hash func-

tion and || denotes concatenation. The Merkle tree is

constructed by organizing the t leaves {l

,. .. ,l

} (in-

cluding the leader’s leaf l

) into a binary tree. For

a level with leaves l

i+1

, as mentioned the parent

node is p

i,i+1

= H(l

||l

i+1

). This process continues,

hashing pairs of nodes until the root R = H(p

||p

)

is computed, where p

, p

are the ﬁnal nodes at the

top level. Veriﬁcation involves checking that t signa-

tures, including σ

, are valid using their public keys

(i.e., Verify(pk

,σ

) = True) and reconstructing

the Merkle root R

′

from the provided signatures and

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation

639

their Merkle paths, as expressed in Algorithm 2. The

message is valid if R

′

= R and the leader’s signature is

included, ensuring authenticity and threshold compli-

ance with O(logt) complexity for path veriﬁcation.

5 EVALUATION

In this section, we evaluate the performance and scal-

ability of the WBFT protocol’s signature tree method.

We conducted two experiments benchmarking its ef-

ﬁciency against other multisignature schemes and as-

sessing its scalability across varying network sizes.

These experiments focus on key metrics such as sign-

ing time, veriﬁcation time, and signature size, which

are critical for resource-constrained robotic networks

in the WAVN system.

5.1 Experimental Setup

All benchmarks in Sections 5.1–5.3 were con-

ducted in a controlled simulation environment. The

WBFT and PBFT protocols were implemented

in Python 3.11 using the TCP sockets for reli-

able message passing and threading for concur-

rent message handling. Cryptographic operations

(Ed25519 signing/veriﬁcation) were performed using

the cryptography library. Experiments were exe-

cuted on a workstation equipped with an Intel Core

i7-1260P (2.50 GHz), 16 GB RAM, running Win-

dows. To emulate network latency and packet loss, we

used the Linux tc/netem utility, introducing random-

ized delays in the range speciﬁed for each experiment

(e.g., 0–1 s in Sec. 5.3). Each data point reﬂects the

average over 20 independent runs. This setup allowed

us to capture both protocol-level message complex-

ity and cryptographic veriﬁcation overhead in con-

ditions approximating bandwidth-constrained robotic

networks.

5.2 Multisignature Scheme

Benchmarking

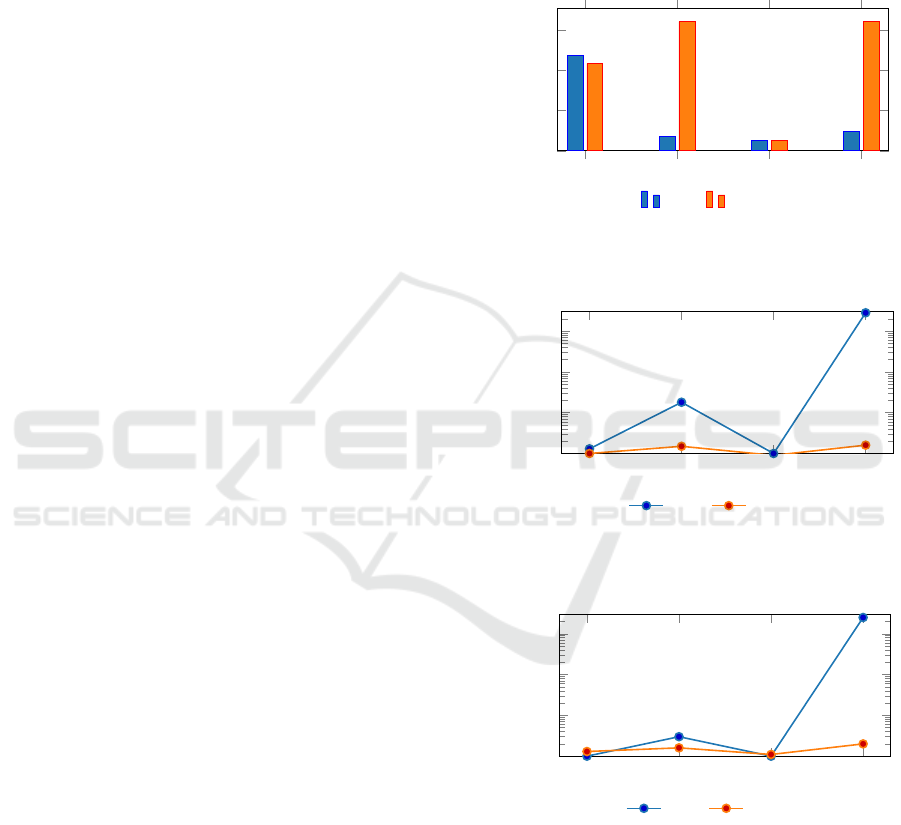
In the ﬁrst experiment, we benchmarked four mul-

tisignature schemes: BLS, aggregate, threshold, and

our novel signature tree method, using a network of

10 nodes with a threshold of 6 signatures, over 20

runs. The experiment measured average signing time,

veriﬁcation time, and signature size for each scheme,

implemented with elliptic curve cryptography. The

signature tree method organizes threshold signatures

into a Merkle tree, enabling efﬁcient veriﬁcation with

O(logt) complexity. Results, visualized in Figure 2,

demonstrate that the signature tree method achieves

a balance of fast veriﬁcation and moderate signa-

ture size, outperforming BLS in veriﬁcation speed

and aggregate signatures in size efﬁciency, making it

well-suited for WBFT’s high-frequency consensus in

robotic networks.

Threshold

Aggregate

Merkle BLS

200

400

600

Method

Signature Size (bytes)

Avg Signature Size (10 Robots, Thr=6)

ECC Ed25519

(a) Signature size

Threshold

Aggregate

Merkle BLS

−3

−2

−1

Method

Time (s)

Avg Signing Time (10 Robots, Thr=6)

ECC Ed25519

(b) Signing time

Threshold

Aggregate

Merkle BLS

−3

−2

−1

Method

Time (s)

Avg Veriﬁcation Time (10 Robots, Thr=6)

ECC Ed25519

Figure 2: Performance comparison of BLS, aggregate,

threshold, and signature tree methods in terms of average

signature size, signing time, and veriﬁcation time for 10

nodes with a threshold of 6, over 20 runs, highlighting the

signature tree method’s efﬁciency for WBFT.

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

640

5.3 Scalability Analysis

In the second experiment, we assessed the scalability

of the same four multisignature schemes by varying

the number of nodes from 5 to 20, with a threshold of

⌊n/2⌋ + 1, over 20 runs. This experiment measured

average signing time, veriﬁcation time, and signa-

ture size for ECC and Ed25519 implementations. Re-

sults in Figure 3 visualize the signature tree method’s

superior veriﬁcation efﬁciency and moderate signa-

ture size across increasing node counts, conﬁrming its

suitability for WBFT’s distributed consensus in large-

scale, fault-tolerant robotic systems.

The comparative analysis of WBFT and PBFT

based on logs from a four-node system (robot 0 as

leader, robot 1, robot 2, robot 3 as followers) re-

veals distinct performance and resilience characteris-

tics. PBFT demonstrates superior efﬁciency, achiev-

ing an average commit time of approximately 0.0067

seconds (ranging from 0.00277 to 0.01155 seconds

across robot 2 and robot 3) compared to WBFT’s

0.027 seconds (ranging from 0.01477 to 0.05403 sec-

onds). This performance edge in PBFT stems from its

streamlined vote-based mechanism, which minimizes

message exchanges by enabling parallel vote pro-

cessing, unlike WBFT’s sequential propose-conﬁrm-

commit phases. PBFT’s ability to commit 14 en-

tries (0–13) versus WBFT’s 12 (0–11) further under-

scores its robustness, particularly in handling Byzan-

tine faults, such as those injected by the leader and

robot 1. However, WBFT’s structured approach offers

unique strengths, particularly in environments priori-

tizing deliberate consensus validation.

5.4 WBFT

An experiment comparing PBFT and WBFT high-

lights distinct differences in their performance un-

der identical conditions, focusing on commit times,

communication efﬁciency, and fault-handling mecha-

nisms. Both systems were tested with 7 robots with

random delay between 0 and 1, using a threshold of 5

(calculated as (⌊2n/3⌋+1), where n = 7). The WBFT

leader log shows the system successfully committing

5 entries with propose times ranging from 0.687 to

1.644 seconds (1.644 is for the Byzantine case) and

a total commit time for entry 0 at 0.63519 seconds.

Communication metrics indicate 36 proposed mes-

sages sent, 26 witnesses received, and 21 committee

messages, with only 10 rewrite attempts, demonstrat-

ing efﬁcient recovery and consensus ﬁnalization. In

contrast, the PBFT leader log reports 6 committed en-

tries, with propose times averaging 0.683–0.686 sec-

onds and faster commit times (e.g., 0.08321 seconds

for entry 0). However, PBFT required 60 rewrite at-

tempts, suggesting higher overhead in handling mes-

sage inconsistencies, despite sending 30 propose mes-

sages, 25 votes, and 60 commit messages. While

PBFT shows slightly faster commit times in optimal

scenarios, WBFT’s lower rewrite attempts indicate

better efﬁciency in managing communication over-

head.

WBFT introduces several strengths over PBFT,

particularly in its use of cryptographic mechanisms

to enhance security and accountability. By employ-

ing Ed25519 signatures at each stage, WBFT ensures

that messages are tamper-proof, preventing unautho-

rized changes during transmission and thwarting at-

tacks like man-in-the-middle. Witnesses are cryp-

tographically linked to the leader’s signed proposal,

making any attempt at forgery or equivocation imme-

diately detectable. WBFT can handle network issues,

even if the leader fails after sending only one pro-

posal, without the risk of messages being altered dur-

ing the voting/witness phase. Additionally, WBFT’s

Merkle tree proof mechanism guarantees that all wit-

nesses are accurately reﬂected in the ﬁnal commit, al-

lowing nodes to independently verify results without

relying on intermediate messages. This contrasts with

PBFT, which depends on simpler message counts and

integrity checks, lacking the robust cryptographic ver-

iﬁcation of WBFT. In scenarios where a leader might

act unreliably, WBFT’s design ensures that even in

optimistic cases, a threshold of (n/2 + 2) nodes can

prevent a malicious leader from disrupting consensus,

offering a stronger defense against such threats.

WBFT provides enhanced fault tolerance and re-

covery mechanisms compared to PBFT. Its dynamic

leader transition ensures system liveness during time-

outs, maintaining consensus even when delays or fail-

ures occur. Public key requests and proof-based com-

mits enable nodes to recover from missing or delayed

messages, improving resilience. WBFT also excels in

accountability by generating cryptographic evidence

to identify and exclude faulty nodes, mitigating risks

like forking, where a leader sends inconsistent pro-

posals to different node subsets. PBFT, while effec-

tive, is more vulnerable to such forking due to its

weaker threshold and lack of signature-based detec-

tion, leading to inefﬁciencies like the observed high

rewrite attempts. WBFT’s ability to produce veriﬁ-

able evidence and maintain consensus with fewer re-

tries underscores its superiority in ensuring both secu-

rity and operational efﬁciency in distributed systems.

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation

641

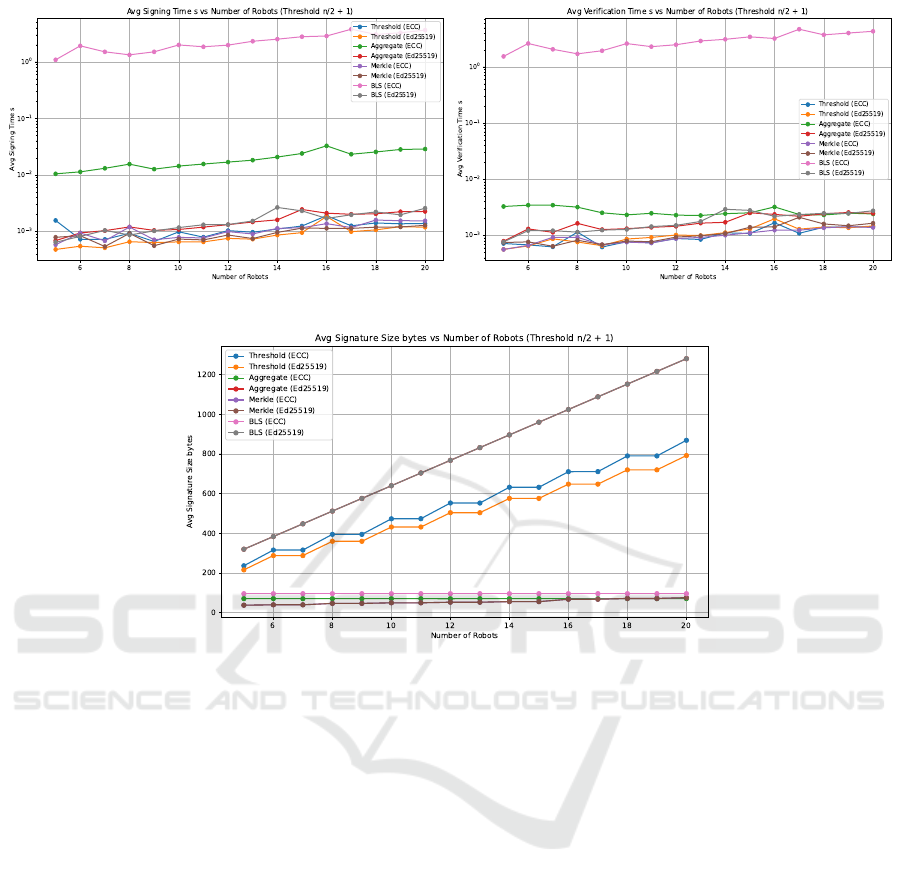
(a) Average signing time (b) Average veriﬁcation time

Figure 3: Scalability comparison of BLS, aggregate, threshold, and signature tree methods in terms of average signing time,

veriﬁcation time, and signature size for 5 to 20 nodes with a threshold of ⌊n/2⌋+1, over 20 runs, demonstrating the signature

tree method’s scalability for WBFT.

6 DISCUSSION

WBFT protocol introduces a novel signature-based

consensus mechanism that signiﬁcantly enhances the

trustworthiness and scalability of distributed con-

sensus in the WAVN system. Our multi-signature

method, leveraging a Merkle tree structure, reduces

veriﬁcation complexity from O(n) to O(logn) for n

signatures, offering a substantial improvement over

traditional aggregate signatures, which scale linearly

with the number of signers (Bellare and Neven, 2006).

The use of Ed25519 signatures, with their compact

32-byte public keys and 64-byte signatures, ensures

fast cryptographic operations, critical for real-time

navigation tasks in resource-constrained robotic net-

works. This efﬁciency is particularly vital in WAVN,

where robots frequently exchange high-volume vi-

sual imagery to construct navigation paths. Addition-

ally, the integration of digital signatures with practical

Byzantine tolerance enhances security. The determin-

istic leader selection via the PoN’s PoS mechanism

further strengthens the protocol by prioritizing reli-

able nodes, ensuring transparency and tamper-proof

leadership assignment in dynamic environments like

agricultural ﬁelds or dense forestry (Paykari et al.,

2024).

Additionally, in mobile robotic settings, intermit-

tent connectivity and delays are common. WBFT’s

threshold-based design means that as long as a con-

nected component of size t = ⌊2n/3⌋ + 1 is main-

tained, consensus can still progress—albeit with

higher latency as witness signatures are collected op-

portunistically. In cases where partitions leave all

components smaller than t, WBFT preserves safety

(no conﬂicting commits) but temporarily halts live-

ness until connectivity resumes. The use of com-

pact Merkle proofs limits the bandwidth cost of re-

transmissions, while leader rotation provides recov-

ery during extended delays. Thus, under adverse con-

ditions WBFT is expected to degrade gracefully in la-

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

642

Table 1: Security comparison of WBFT and PBFT.

Dimension PBFT (Message Counting) WBFT (Cryptographic Proofs)

Commit Rule Relies on counting prepare/commit

messages; vulnerable to equivocation

Requires t = ⌊2n/3⌋ + 1 valid digital

signatures, embedded in a Merkle root

Fault Detection Limited; inconsistent views not easily

attributable

Misbehavior produces veriﬁable cryp-

tographic evidence (invalid or missing

signatures)

Leader Accountability Weak; malicious leaders may fork pro-

posals without proof

Strong; equivocation leaves signed evi-

dence traceable to leader

Recovery from Delays Rewrites and retries; higher communi-

cation overhead

Compact witness proofs (O(log n)) al-

low independent veriﬁcation

Scalability under

Byzantine Behavior

High retries, costly in bandwidth Safety preserved with fewer retries;

evidence enables exclusion of faulty

nodes

tency while retaining safety, with future work aimed

at adaptive timeouts and opportunistic forwarding to

better match the dynamics of robotic mesh networks.

To formalize the contrast between WBFT and

PBFT, Table 1 highlights how WBFT’s signature-

based design strengthens security compared to

PBFT’s message-counting approach. Whereas PBFT

relies primarily on message tallies that can be equiv-

ocated without trace, WBFT embeds every commit in

cryptographic evidence, enabling both stronger safety

and accountability. This design reduces the risk of

forks, facilitates faster recovery, and ensures that ma-

licious behavior can be attributed and penalized.

Despite its strengths, WBFT faces several limi-

tations that warrant consideration, such as construct-

ing the Merkle tree, introducing computational over-

head, particularly in dynamic networks with frequent

node joins or exits, which may impact performance

in large-scale deployments or the behavior of the net-

work in case of a byzantine leader or a non-responsive

leader.

Future work aims to address these limitations and

further enhance WBFT’s performance and adaptabil-

ity. Developing an adaptive fault tolerance mech-

anism that dynamically adjusts the threshold based

on network conditions could improve resilience in

asynchronous settings, potentially achieving optimal

fault tolerance without sacriﬁcing liveness. Intro-

ducing a second or third leader to the markle tree

can be another alternative. Exploring sharding tech-

niques to partition the network into smaller consen-

sus groups could reduce communication overhead

and enhance scalability, particularly for large-scale

robotic swarms. Additionally, optimizing the Merkle

tree construction process by leveraging incremental

hashing or parallel processing could mitigate com-

putational overhead in dynamic node sets. Inte-

grating lightweight cryptographic alternatives, such

as post-quantum signature schemes, could future-

proof WBFT against emerging threats while main-

taining efﬁciency. Finally, incorporating machine

learning-based anomaly detection to identify and

isolate Byzantine nodes in real-time could further

strengthen the protocol’s security, ensuring robust

consensus in adversarial environments. These ad-

vancements will enhance WBFT’s applicability to a

broader range of distributed robotic systems, reinforc-

ing its role as a scalable and fault-tolerant consensus

mechanism for WAVN and similar applications.

7 CONCLUSION

This paper proposed the Witness Byzantine Fault Tol-

erance (WBFT) protocol, a scalable and secure con-

sensus mechanism tailored for Wide Area Visual Nav-

igation (WAVN) in robotic systems. By combining

Ed25519 threshold signatures, a Merkle tree struc-

ture, and a novel Proof-of-Navigation (PoN) leader

selection approach, WBFT achieves efﬁcient consen-

sus with reduced communication overhead and strong

Byzantine fault resilience. Experimental results val-

idate WBFT’s performance advantages over tradi-

tional schemes like PBFT and BLS-based multisig-

natures, particularly in veriﬁcation speed, scalabil-

ity, and fault recovery. While Merkle tree construc-

tion introduces some overhead, WBFT remains well-

suited for resource-constrained, adversarial environ-

ments. Future work will optimize tree construction,

explore adaptive thresholds, and enhance resilience

using machine learning and post-quantum cryptogra-

phy, extending WBFT’s applicability to broader de-

centralized robotic networks.

Witness Byzantine Fault Tolerance with Signature Tree and Proof-of-Navigation for Wide Area Visual Navigation

643

REFERENCES

Abraham, I., Chouatt, E., Gilad, Y., Stern, G., and Yak-

oubov, S. (2025). Asynchronous algorand: Reaching

agreement with near linear communication and con-

stant expected time. In Proceedings of the ACM Sym-

posium on Principles of Distributed Computing, pages

28–38.

Aditya, U. S., Singh, R., Singh, P. K., and Kalla, A. (2021).

A survey on blockchain in robotics: Issues, opportuni-

ties, challenges and future directions. Journal of Net-

work and Computer Applications, 196:103245.

Bacho, R. and Loss, J. (2022). On the adaptive security of

the threshold bls signature scheme. In proceedings of

the 2022 ACM SIGSAC conference on computer and

communications security, pages 193–207.

Bellare, M. and Neven, G. (2006). Multi-signatures in the

plain public-key model and a general forking lemma.

In Proceedings of the 13th ACM conference on Com-

puter and communications security, pages 390–399.

Bisheh-Niasar, M., Azarderakhsh, R., and Mozaffari-

Kermani, M. (2021). Cryptographic accelerators for

digital signature based on ed25519. IEEE Transac-

tions on Very Large Scale Integration (VLSI) Systems,

29(7):1297–1305.

Boneh, D., Drijvers, M., and Neven, G. (2018).

Bls multi-signatures with public-key ag-

gregation. URL: https://crypto. stanford.

edu/dabo/pubs/papers/BLSmultisig. html.

Castro, M., Liskov, B., et al. (1999). Practical byzantine

fault tolerance. In OsDI, volume 99, pages 173–186.

Chu, H., Gerhart, P., Rufﬁng, T., and Schr

oder, D. (2023).

Practical schnorr threshold signatures without the al-

gebraic group model. In Annual International Cryp-

tology Conference, pages 743–773. Springer.

Huang, B., Peng, L., Zhao, W., and Chen, N. (2022).

Workload-based randomization byzantine fault toler-

ance consensus protocol. High-Conﬁdence Comput-

ing, 2(3):100070.

Kramer, M., Gerstmayer, F., and Hausladen, J. (2018).

Evaluation of libraries and typical embedded systems

for ecdsa signature veriﬁcation for car2x communi-

cation. In 2018 IEEE 23rd International Conference

on Emerging Technologies and Factory Automation

(ETFA), volume 1, pages 1123–1126. IEEE.

Liu, X. and Zhu, J. (2024). An improved practical byzantine

fault tolerance algorithm for aggregating node prefer-

ences. Scientiﬁc Reports, 14(1):31200.

Lyons, D. M. and Rahouti, M. (2023). Wavn: Wide area

visual navigation for large-scale, gps-denied environ-

ments. In 2023 IEEE International Conference on

Robotics and Automation (ICRA), pages 2039–2045.

IEEE.

Paykari, N., Alfatemi, A., Lyons, D. M., and Ra-

houti, M. (2025a). Integrating robotic naviga-

tion with blockchain: A novel pos-based approach

for heterogeneous robotic teams. arXiv preprint

arXiv:2505.15954.

Paykari, N., Lyons, D., and Rahouti, M. (2024). Ro-

bostake: Pioneering cooperative navigation with a

novel blockchain-powered proof-of-stake in robotic

teams. In 2024 IEEE International Conference on

Omni-layer Intelligent Systems (COINS), pages 1–4.

IEEE.

Paykari, N., Rahouti, M., and Lyons, D. M. (2025b). A

novel blockchain-driven proof-of-stake model for co-

operative navigation in visual homing robotic teams.

Distributed Ledger Technologies: Research and Prac-

tice.

Sadikin, M. A. and Wardhani, R. W. (2016). Implementa-

tion of rsa 2048-bit and aes 256-bit with digital signa-

ture for secure electronic health record application. In

2016 International Seminar on Intelligent Technology

and Its Applications (ISITIA), pages 387–392. IEEE.

Wu, Y., Wu, L., and Cai, H. (2023). Reinforced practi-

cal byzantine fault tolerance consensus protocol for

cyber physical systems. Computer Communications,

203:238–247.

Yang, Z. and Bajwa, W. U. (2019). Byrdie: Byzantine-

resilient distributed coordinate descent for decentral-

ized learning. IEEE Transactions on Signal and In-

formation Processing over Networks, 5(4):611–627.

TISAS 2025 - Special Session on Trustworthy and Intelligent Smart Agriculture Systems: AI, Blockchain, and IoT Convergence

644