Automated Computational Workflow for the Parametric Design and

Optimization of a 3D-Printed Fin Ray Effect Soft Robotic Finger

Rodrigo Antunes

1,2 a

, Luan Lang

, Martim Lima de Aguiar

1,2 c

, Nuno José Matos Pereira

1,2 d

Thiago Assis Dutra

1,2 e

, Yebo Lu

and Pedro Dinis Gaspar

1,2 g

C-MAST, Centre for Mechanical and Aerospace Science and Technologies,

University of Beira Interior, Calçada Fonte do Lameiro 6, 6200-358, Covilhã, Portugal

Department of Electromechanical Engineering, University of Beira Interior,

Calçada Fonte do Lameiro 6, 6200-358, Covilhã, Portugal

College of Mechanical Engineering, Jiaxing University, Jiaxing, Zhejiang province, 314001, China

Keywords: Soft Robotic Finger, Computational Design, Fin Ray Effect, Parametric Optimization,

Finite Element Analysis, Additive Manufacturing, PyAnsys, Soft Grippers.

Abstract: The design of soft grippers is challenged by the complex, non-linear coupling of material properties, geometry,

and control, rendering traditional design methods inefficient. To address this, this paper presents an automated

computational workflow for the parametric design and optimization of a 3D-printed Fin Ray Effect soft

robotic gripper finger. The tool establishes a closed-loop digital thread, connecting a web-based parametric

design interface using FreeCAD to a finite element analysis backend driven by PyAnsys. A parametric study

was conducted, varying the number of internal crossbeams from 1 to 16, to analyse the gripper's performance

using an experimentally validated hyperelastic model for TPU 60A. The results show a trade-off between

contact pressure and pressure distribution, with an optimal configuration of 14-16 crossbeams identified for

applications requiring a gentle grip with low-pressure concentrations. The developed workflow proved to be

an effective method for rapidly iterating through designs and identifying an optimal solution, showcasing the

power of automated simulation in the Design for Additive Manufacturing (DfAM) process.

1 INTRODUCTION

The field of robotics is evolving from a predominant

emphasis on precision through rigidity toward an

increasing integration of adaptability through

compliance. For decades, rigid-linked robots have

been the standard, however, they face considerable

challenges when operating in unstructured, human-

centric environments where safe interaction is

required. Soft robotics presents an alternative, using

materials such as elastomers and gels with moduli of

elasticity, typically ranging from 10



to 10



Pa,

which are comparable to biological tissues (Zhang et

https://orcid.org/0009-0002-6599-6905

https://orcid.org/0000-0002-2857-3092

https://orcid.org/0000-0003-0672-0378

https://orcid.org/0000-0001-7177-751X

https://orcid.org/0000-0002-3576-5703

https://orcid.org/0000-0002-8995-370X

https://orcid.org/0000-0003-1691-1709

al., 2020). This material choice gives soft robotic

grippers an inherent compliance (Nonaka et al.,

2023), which enables them to passively adapt to

objects of diverse and irregular shapes, absorb impact

energy and reduce the need for complex control

systems through a concept known as embodied

intelligence (Ponce et al., 2021).

However, the very nature of these materials

creates design challenges (Stella & Hughes, 2023),

unlike in rigid robotics, the behaviour of a soft robot

is governed by a tight, nonlinear coupling of its

material properties, geometric morphology, and

control inputs. This complexity renders traditional,

Antunes, R., Lang, L., Lima de Aguiar, M., Pereira, N. J. M., Assis Dutra, T., Lu, Y. and Gaspar, P. D.

Automated Computational Workﬂow for the Parametric Design and Optimization of a 3D-Printed Fin Ray Effect Soft Robotic Finger.

DOI: 10.5220/0013944900003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 577-584

ISBN: 978-989-758-770-2; ISSN: 2184-2809

577

intuition-based design methods inefficient and has

created a need for advanced computational tools to

navigate the design space effectively (Xie, Pinskier,

et al., 2024).

To address this challenge, this paper presents an

integrated computational workflow that automates

the design and analysis of Fin Ray Effect (FRE) Soft

Robotic Gripper Fingers (SRGF). The framework

uses a web application to parametrically generate

geometries in FreeCAD, which are then analysed

using a Finite Element Method (FEM) simulation

controlled programmatically via the PyAnsys library.

The utility of this pipeline is demonstrated through a

parametric study investigating the influence of

internal crossbeam density on grasping forces and

contact pressures, thereby contributing a practical

tool for the principled design of high-performance

soft robotic grippers.

2 LITERATURE REVIEW

2.1 Computational Approaches to

Complex Design

Despite these conceptual advantages, the potential of

soft grippers is constrained by the complexity

inherent in their design (Stella & Hughes, 2023).

Addressing these design complexities effectively

requires moving beyond intuition-based approaches

toward computational methods capable of navigating

the high-dimensional and nonlinear design space of

soft robotic grippers (Yi et al., 2025).

To overcome this, the field has increasingly

embraced computational simulation as a tool for

creating principled and optimized designs (Xie,

Pinskier, et al., 2024). This approach formalizes the

creative design process into an optimization task

within a defined parameterized design space (Stella &

Hughes, 2023). Researchers have focused on

parameterizing key design variables, such as the

spatial stiffness distribution for balancing compliance

and force transmission, the geometry of pneumatic

chambers for actuation (Navez et al., 2025), the finger

arrangement and frame design, the selection and

combination of materials to achieve controlled

motion (Jin et al., 2024). The search for optimal

parameters within this complex landscape has led to

the widespread adoption of artificial intelligence

techniques (Xie, Wang, et al., 2024). Methods such as

Genetic Algorithms—which use a fitness function

evaluated via simulation to evolve a population of

designs —and Deep Reinforcement Learning have

become mainstays in the field. A significant

bottleneck, however, is the computational cost of

fitness evaluation, which has been addressed by the

use of Neural Network Surrogates to accelerate the

process (Garcia et al., 2024).

Beyond parameter-based methods, more free-

form approaches like topology optimization have

been used to discover novel structures (Xie, Pinskier,

et al., 2024). Furthermore, a holistic view recognizes

that performance is determined by the synergy

between morphology and control, leading to the goal

of co-design—the simultaneous optimization of the

robot's body and brain (Yi et al., 2025).

2.2 High-Fidelity Simulation with the

Finite Element Method

At the core of any computational design framework

resides the simulation engine, which predicts the

physical behaviour of the gripper. The FEM allows

for modelling hyperelastic body dynamics (Elgström,

2014), it is particularly well-suited for the challenges

of soft robotics, which involve large, nonlinear

material deformations. The process involves the

discretization of the geometry into simpler elements

and nodes, the reformulation of governing equations

into a weak form, and the iterative solution of a large

nonlinear system of equations, often using the

Newton-Raphson method (Megan & Croop, 2014).

Modelling the hyperelastic behavior of

elastomers was achieved using constitutive models

such as the Neo-Hookean, Mooney-Rivlin, Yeoh and

Polynomial models. An important step for simulation

accuracy is the derivation of material coefficients by

fitting these models to experimental test data, as these

parameters are not typically found in datasheets

(ANSYS Inc., 2017).

For gripper design, FEM allows for the simulation

of contact mechanics—a challenging and non-smooth

phenomenon. This includes enforcing non-

penetration constraints, modelling friction, and

analysing the resulting forces and pressure

distributions during a grasp (Dassault Systèmes,

2018). For tasks that demand the highest degree of

physical accuracy and validation, industry-standard

commercial FEM packages like Ansys and ABAQUS

are the preferred choice and are considered the gold

standard for design verification (Han et al., 2020).

The constant tension between simulation fidelity and

computational speed remains a central engineering

dilemma, driving the development of techniques like

Reduced Order Modeling (Guo & Hesthaven, 2018)

and learned surrogate models to manage this trade-off

(Navez et al., 2025).

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

578

2.3 Integrated and Automated

Workflows

The ultimate objective in computational design is the

creation of fully automated pipelines that can

autonomously discover, optimize, and validate novel

designs. Recent breakthroughs in differentiable

simulation and Quality Diversity (QD) algorithms are

bringing this vision closer to reality (Xie, Wang, et

al., 2024). Differentiable simulation allows for the

use of highly efficient, gradient-based optimization

algorithms (Connolly et al., 2015), while QD

algorithms like MAP-Elites aim to generate a diverse

archive of high-performing solutions rather than a

single optimum (Xie, Pinskier, et al., 2024).

A technological enabler for automation is the

development of Python libraries that provide

programmatic access to powerful commercial

solvers. The PyAnsys project, for example, is a

collection of Python packages that enables users to set

up, run, and post-process Ansys simulations entirely

through scripts, bridging the gap between high-

fidelity analysis and flexible automation (Maronehitz,

2024). These integrated, multi-physics workflows

have been successfully applied to design complex

structures. A powerful example is the framework

developed for designing the GelSight Fin Ray, a

compliant finger with embedded tactile sensing,

which used a dual simulation pipeline to co-design its

mechanical and sensory components (Liu et al., 2023;

Liu & Adelson, 2022). This demonstrates both the

viability of integrated simulation-driven design and

the continued relevance of specific, high-

performance structures like the FRE SRGF. Our work

builds upon these advancements by presenting a

specialized, integrated tool that leverages the power

of PyAnsys to automate the design and detailed

contact area and pressure analysis of FRE SRGF,

addressing the practical need for accessible and

efficient design-to-analysis pipelines for specific,

high-performance structures within the broader

landscape of soft robotics research.

2.4 Influence of Internal Number of

Ribs in Fin Ray Effect Design

Finger

An area of research within Fin Ray Effect finger

design is the optimization of its internal structure, as

the crossbeams (also known as ribs), are components

that significantly influence the finger’s overall

stiffness and gripping performance. The number and

angle of crossbeams have been identified as

parameters impacting the balance between flexibility

and force application (Shin et al., 2021; Suder et al.,

2021). Shin et al., (2021) systematically investigated

the effect of varying the number of crossbeams on

finger performance, concluding that it had a

significant impact on displacement. The analysis

showed that as the number of crossbeams increased,

the stress applied to a gripped object also increased,

while the fingertip's displacement decreased due to

the higher overall stiffness. This highlights a direct

trade-off between gripping force and flexibility.

Through their optimization process, the researchers

determined that a configuration with five crossbeams

provided the optimal balance, achieving the necessary

displacement for a complete grip while maximizing

force. Suder et al., (2021) also explored this

relationship by testing fingers with 1 to 9 crossbeams.

Using a deflection coefficient to mathematically

evaluate the finger's ability to wrap around an object,

the study found that the most suitable structure for

wrapping was not the one with the highest

deformation. While the finger with only one

crossbeam deformed the most under a constant load,

it did not achieve the best wrapping score. Instead, the

analysis identified a structure with six crossbeams as

having the best performance in terms of its wrapping

capability. Table 1 summarizes the findings regarding

the effect of the number of crossbeams in the Fin Ray

finger design.

Table 1: Summary of Rib Number Influence in Fin Ray

Effect Fingers Design.

Study Shin et al., (2021)

Suder et al.,

(2021)

Crossbeams

Investigated

Varied number,

with a final design

of 5

1 to 9 crossbeams

Finding on

Stiffness &

Deformation

Increasing the nº

of crossbeams

decreased finger

displacement,

resulting in a

stiffer structure.

The finger with

only 1 crossbeam

showed the

greatest

deformation.

Finding on

Force &

Wrapping

Increasing the nº

of crossbeams

increased the

stress applied to

the object.

Wrapping ability

was the primary

metric; it did not

directly correlate

with maximum

deformation.

Optimal

Number &

Rationale

5 crossbeams

were found to be

optimal for

balancing the

necessary

displacement and

force for a

complete grip.

6 crossbeams

provided the best

wrapping

capability, as

determined by the

lowest deflection

coefficient.

Automated Computational Workﬂow for the Parametric Design and Optimization of a 3D-Printed Fin Ray Effect Soft Robotic Finger

579

3 MATERIALS AND METHODS

To facilitate the rapid design and optimization of a

soft robotic gripper, a comprehensive computational

tool was developed. This tool creates a closed-loop

digital thread by integrating a web-based user

interface for parametric geometry generation with a

backend engine for automated finite element analysis

(FEA) and data extraction.

3.1 Integrated Design and Simulation

Pipeline

The tool is architected as a complete pipeline

organized by a central Python script, which manages

the user interface and coordinates the execution of

specialized sub-processes for CAD generation and

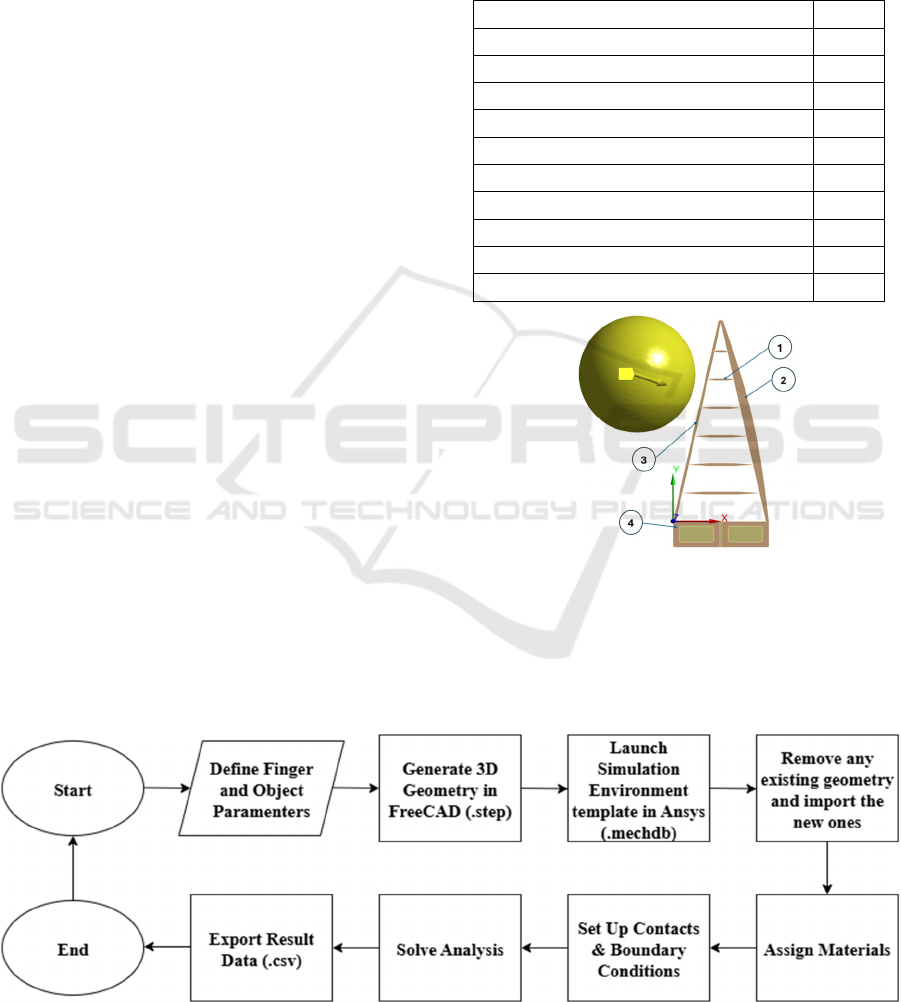
FEA simulation. The workflow (shown in Figure 2)

begins with a user defining the gripper's geometric

parameters via the web interface. These parameters

are then passed to a Free CAD scripting engine that

generates the required .step files for the components.

Subsequently, the .step files are imported by a

PyAnsys script, which automates the setup, solution,

and post-processing within Ansys Mechanical. The

final stage of the pipeline involves the script

outputting the time-dependent performance data as

CSV files, enabling quantitative comparison between

design iterations.

3.2 Parametric Design Generation via

Web Application

A web application built with the Gradio library serves

as the front-end, allowing users to define the finger's

design parameters (Table 2). These parameters are

sent to a FreeCAD script that programmatically

generates the 3D models of the finger, a target sphere,

and a base connector, which are then exported as

STEP files. For this study, a parametric analysis was

performed by varying the number of crossbeams from

1 to 16, as this is a key parameter in the Fin Ray Effect

design. All other geometric parameters, including the

50 mm sphere diameter, were held constant.

Table 2: Design parameters used by the developed

computational tool to create the Fin Ray Effect Finger.

Parameter Unit

Overall fin

er len

th [mm]

Finger base width [mm]

Fin

er de

th [mm]

Fin

er frame thickness [mm]

Rear frame side amplitude [mm]

Number of cross

eams [-]

Beam thickness [mm]

Minimum beam thickness [mm]

Taper ratio [-]

Crossbeam an

le [de

]

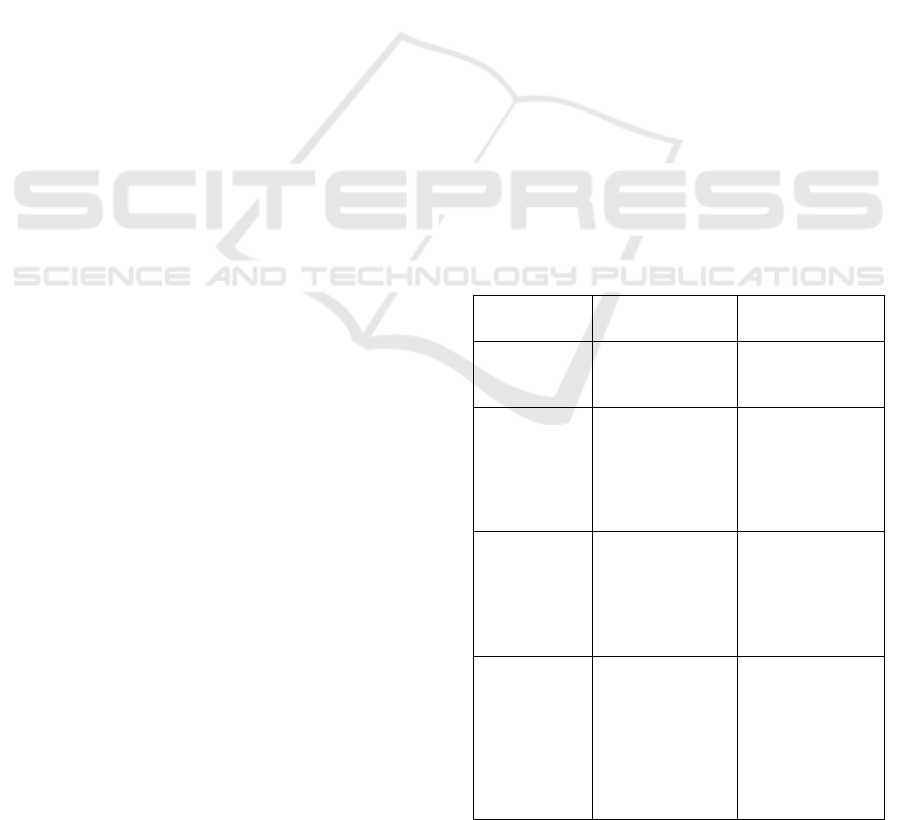
Figure 1: Architecture of the soft robotic finger and

simulation setup. The finger consists of (1) Crossbeams, (2)

a flexible rear spine, (3) the contact side, and (4) the finger

base. A displacement is applied to the target sphere to

simulate contact.

Figure 2: Flowchart of the automated computational workflow.

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

580

3.3 Automated Finite Element Analysis

The simulation is controlled by a PyAnsys script that

automates the workflow in Ansys Mechanical. The

script begins by opening a template project, replacing

any existing geometry with the newly generated

STEP files. Materials are then assigned

programmatically, with a hyperelastic model for the

TPU 60A finger and structural steel for the other

components. The script automatically defines the

necessary frictionless and bonded contacts and

applies the boundary conditions for the linear

actuation model. The analysis uses 10-node

tetrahedral elements with contacts modelled using an

Augmented Lagrange formulation.

3.4 Material Model Characterization

The mechanical behaviour of the flexible gripper

material, TPU 60A, was determined through

experimental testing in previous works (Lang et al.,

2025). From this characterization, the stress-strain

data was used as an input for the computational

model. This experimental data was imported into

Ansys Engineering Data, where the 2nd Order

Polynomial hyperelastic model was selected for

providing the best fit (R² = 0.9993), ensuring the

simulated material behaviour reflects the real-world

performance of the 3D-printed TPU 60A.

3.5 Simulation and Post-Processing

Once the model is generated, the script initiates the

static structural analysis in Ansys Mechanical. To

analyse the gripping performance, a Contact Tool is

programmatically added to the solution and scoped

specifically to the finger-object interface. After the

solve is complete, the script automatically exports

key results, such as the Force Reaction at the finger's

base and the Contact Pressure distribution, to CSV

files for quantitative analysis. This automated data

extraction is critical for comparing the performance

of different parametric designs.

4 RESULTS

The computational tool was employed to conduct a

parametric study investigating the influence of the

number of internal crossbeams on the performance of

the FRE SRGF. A series of simulations was executed

with 1, 2, 3, 4, 6, 8, 10, 12, 14, and 16 crossbeams,

while all other geometric and simulation parameters

were held constant, as defined in the materials and

methods section. Four performance indicators—

maximum contact pressure ( 𝑃



), final reaction

force (𝐹



), average contact pressure (𝑃



)—were

recorded at the final time step of each simulation to

evaluate the gripper’s design. A pressure uniformity

ratio (𝑈



) was calculated according to Equation (1):

𝑈





𝑃



𝑃



(1)

This ratio serves as an indicator of grasping

quality. In an ideal case, the contact pressure is evenly

distributed, and the ratio approaches 1.

4.1 Effect on Maximum Contact

Pressure

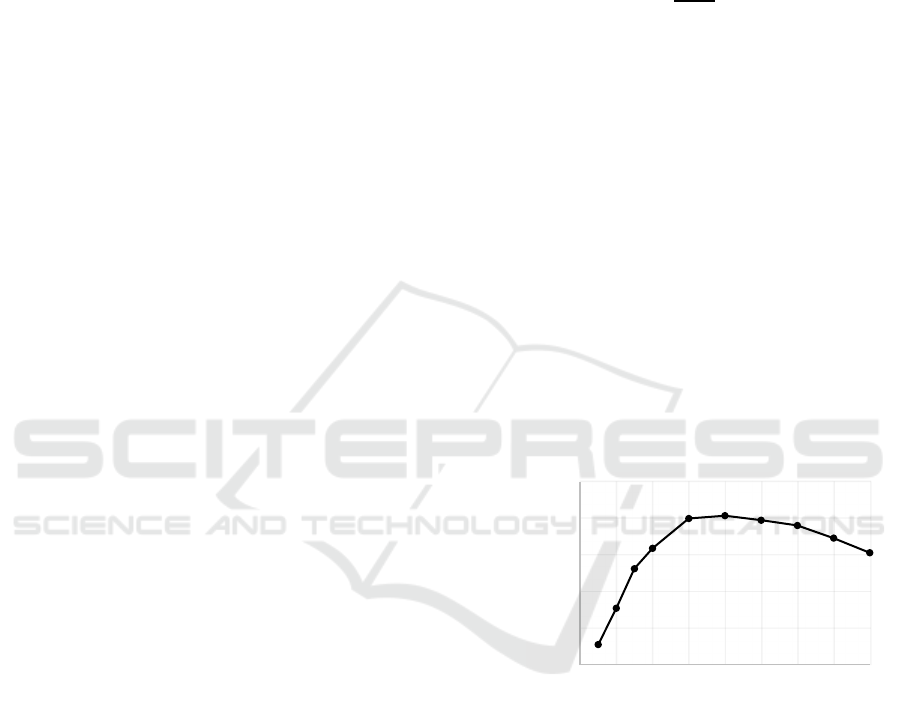
The relationship between the number of crossbeams

and the resulting maximum contact pressure is shown

Figure 3

. The trend is non-linear. The maximum

pressure increases sharply from 0.03 MPa with one

crossbeam to a peak of 0.20 MPa for designs with 6,

8, and 10 crossbeams. This initial rise corresponds to

the increase in stiffness, which concentrates the

gripping force onto smaller areas. Beyond 10

crossbeams, a clear downward trend is observed, with

the maximum pressure decreasing to 0.15 MPa for the

16-crossbeam design.

𝑃



[MPa]

Number of crossbeams

Figure 3: Maximum Contact Pressure applied in the last

step of the simulation for each design configuration.

4.2 Effect on Gripping Force

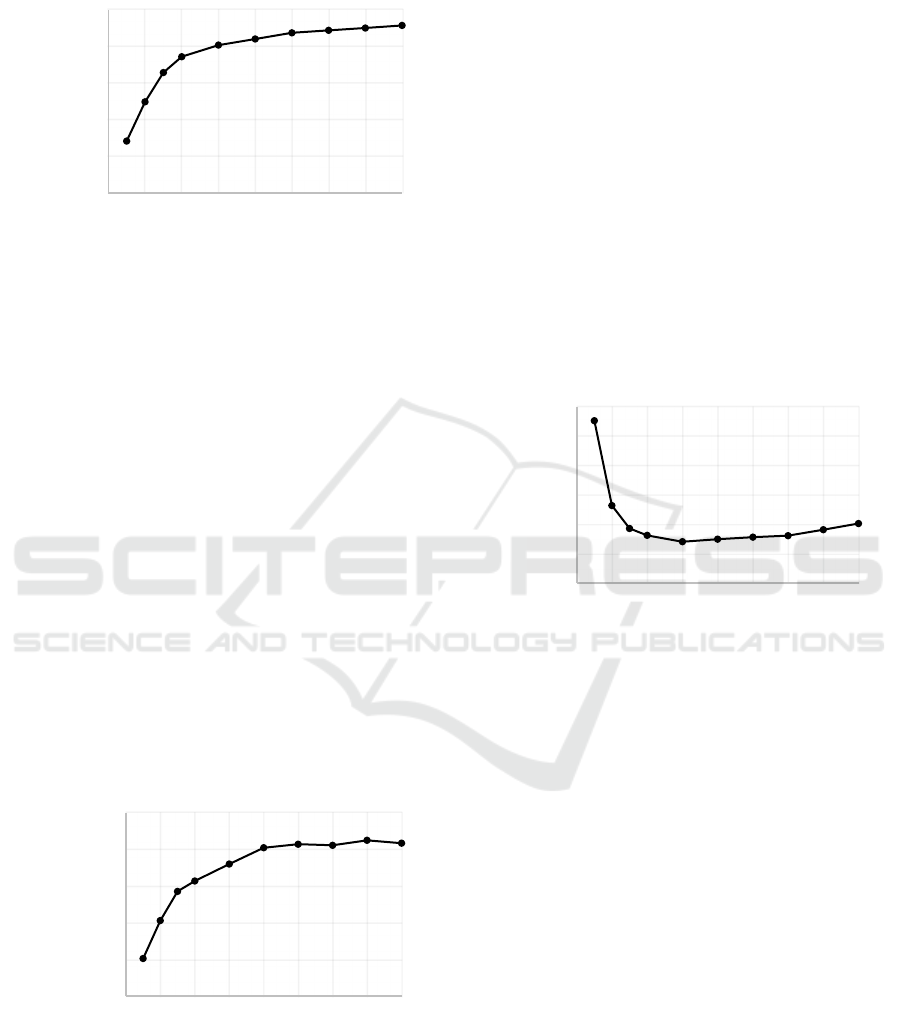
The total reaction force indirectly indicates the

overall gripping force exerted by the finger and is

presented in

Figure 4

. The results show a clear and

consistent trend as the number of crossbeams

increases the reaction force steadily rises. The force

increases from 0.85 N for a single crossbeam to a

maximum of 1.67 N for the 16-crossbeam design.

This indicates that adding more crossbeams

progressively increases the structural stiffness of the

0.00

0.05

0.10

0.15

0.20

0.25

0246810121416

Automated Computational Workﬂow for the Parametric Design and Optimization of a 3D-Printed Fin Ray Effect Soft Robotic Finger

581

finger, allowing it to generate a stronger grip for the

same actuation displacement.

𝐹



[N]

Number of crossbeams

Figure 4: Force Reaction for each design configuration.

This condition together with the decrease of

maximum pressure after 8 crossbeams demonstrates

that a higher number of crossbeams distributes the

load more effectively, reducing the intensity of

pressure "hot spots."

4.3 Effect on Average Contact Pressure

The average contact pressure across the entire contact

patch is presented in

Figure 5

. This metric shows a

consistent upward trend, rising from 1.51 × 10

MPa

for a single crossbeam to a peak of 3.13 × 10

MPa

for the 14-crossbeam design. Unlike the maximum

pressure, the average pressure does not decrease with

a higher number of crossbeams, it is almost constant

from the 10-crossbeam design to 16-crossbeam

design. This suggests that while the peak pressures

are reduced, the overall pressure across the contact

area remains high and becomes more uniform,

indicating a more efficient and distributed grip.

𝑃



[MPa]

Number of crossbeams

Figure 5: Average Contact Pressure applied in the last step

of the simulation for each design configuration.

4.4 Effect on Pressure Distribution

Uniformity

To quantify the uniformity of the grip, the ratio of the

average pressure to the maximum pressure was

calculated. A higher ratio signifies a more evenly

distributed load. The results, plotted in Figure 6, show

that the 1-crossbeam design had an exceptionally high

uniformity ratio of 0.055, which is a consequence of

its very low stiffness that results in low reaction force

and max pressure. After this initial point, the

uniformity drops significantly, reaching a minimum

at 6 crossbeams where 𝑈



0.014. As more

crossbeams are added beyond this point, the pressure

distribution becomes progressively more uniform,

with the ratio steadily climbing to a new peak of 𝑈



0.023 for the 16-crossbeam design. This trend

suggests that a high number of crossbeams

contributes to achieving an even and gentle grip.

𝑈



[-]

Number of crossbeams

Figure 6: Ratio between Average Contact Pressure and

Maximum Contact Pressure in each configuration as an

evaluation parameter for pressure distribution.

4.5 Visual Analysis of Contact Pressure

Maps

To visualize the qualitative trends underlying the

quantitative data, Figure 7 displays the

contact‑pressure maps for four representative designs

containing 2, 6, 10 and 14 cross‑beams.

2 crossbeams (Figure 7a) – A narrow, vertically

aligned band of increased contact pressure is observed.

Local peaks occur where the lower crossbeam touches

the object and at the fingertip, whereas a small zone in

the top region shows lower contact pressure. The

contact area is therefore large, but the finger is

compliant and offers limited grasping stiffness, as

indicated by the narrow contact region.

6 crossbeams (Figure 7b) – The pressure field

becomes broader and lower. A zone of low pressure

appears from mid‑height to near the top, bounded by

a second cross‑beam footprint. A pronounced

0.50

0.75

1.00

1.25

1.50

1.75

0246810121416

0.001

0.0015

0.002

0.0025

0.003

0.0035

0 2 4 6 8 10 12 14 16

0.01

0.02

0.03

0.04

0.05

0.06

0246810121416

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

582

pressure peak appears at the fingertip, indicating a

configuration that may damage delicate objects.

As the number of crossbeams further increases to

10 (Figure. 7c) and 14 (Fig. 7d), the contact area

continues to expand, and the load distribution

becomes more uniform. Crucially, this reduces the

maximum pressure at the fingertip, leading to a more

stable and gentler grasp.

(a) (b) (c) (d)

Figure 7: Finger Deformation and Contact Pressure Map at

the end of the simulation for different number o

crossbeams in the design, a) 2, b) 6, c) 10, d) 14.

Adding crossbeams initially raises the local peak

pressure at the fingertip but further increases

progressively equalise the pressure over the finger,

reducing the peak value and improving grasp quality

while maintaining adequate stiffness.

5 CONCLUSIONS

In this work, a comprehensive computational tool for

the design and optimization of a 3D-printed, Fin Ray

Effect robotic gripper was developed and validated.

By integrating a parametric web interface with a

FreeCAD geometry engine and a PyAnsys-driven

finite element analysis backend, a closed-loop digital

thread was created, enabling the rapid iteration and

quantitative evaluation of different gripper designs.

The parametric study, which varied the number of

internal crossbeams from 1 to 16

(1,2,3,4,6,8,10,12,14,16), revealed a complex and

non-linear relationship between number of

crossbeams and gripping performance. The results

demonstrate that the relation between contact

pressure, maximum pressure and grasping quality is

not linear. Designs with 6 to 10 crossbeams exhibited

a higher maximum contact pressure but at the cost of

a poor pressure uniformity, characterized by a

pressure peak near the fingertip. Conversely, designs

with a high number of crossbeams (above 14) showed

a marked improvement in performance in terms of

pressure distribution. These configurations reduced

the maximum contact pressure while simultaneously

increasing the pressure distribution uniformity. The

visual analysis of the contact pressure maps provided

a qualitative confirmation of these findings,

illustrating the transition from a focused, high-

pressure grip to a more compliant and evenly

distributed grip as the number of crossbeams was

increased. Based on the simulation data, it can be

concluded that for applications where minimizing

pressure to a gripped object’s surface is essential, a

design with a higher number of crossbeams (e.g., 14-

16) represents an optimal solution. This configuration

provides a balance of a low maximum pressure, a

bigger gripping force and a uniform pressure

distribution.

Future work will investigate additional

parameters influencing the performance of FRE

SRGF, including crossbeam angles and material

selection. Additionally, the fingertip design must be

reevaluated to mitigate the maximum pressure

hotspot and improve delicate object handling.

ACKNOWLEDGEMENTS

These results are within the research activities of

project “ROBOTA-SUDOE - Robotics, Automation,

and Digitalization as Drivers of Competitiveness and

Growth for SMEs” (S1/1.1/P0125), which is co-

funded by the European Union through the European

Regional Development Fund (ERDF) and national

funds, under the territorial cooperation Interreg

Europe Programme 2021–2027 (eSUDOE 2021-

2027). This research was partially funded by the

Portuguese Foundation for Science and Technology,

I.P. (FCT, I.P.) FCT/MCTES through national funds

(PIDDAC), under the R&D Unit C-MAST/Center for

Mechanical and Aerospace Science and

Technologies, reference: Projects UIDB/00151/2020

(https://doi.org/10.54499/UIDB/00151/2020) and

UIDP/00151/2020

(https://doi.org/10.54499/UIDP/00151/2020)

Automated Computational Workﬂow for the Parametric Design and Optimization of a 3D-Printed Fin Ray Effect Soft Robotic Finger

583

REFERENCES

ANSYS Inc. (2017). Appendix 4A: Hyperelasticity.

Connolly, F., Polygerinos, P., Walsh, C. J., & Bertoldi, K.

(2015). Mechanical programming of soft actuators by

varying fiber angle. Soft Robotics, 2(1), 26–32.

Dassault Systèmes. (2018). Modeling Rubber and

Viscoelasticity with Abaqus.

Elgström, E. (2014). Practical implementation of

hyperelastic material methods in FEA models.

Garcia, M., Esquen, A.-C., Sabbagh, M., Grace, D.,

Schneider, E., Ashuri, T., Voicu, R. C., Tekes, A., &

Amiri Moghadam, A. A. (2024). Soft Robots:

Computational Design, Fabrication, and Position

Control of a Novel 3-DOF Soft Robot. Machines, 12(8),

539.

Guo, M., & Hesthaven, J. S. (2018). Reduced order

modeling for nonlinear structural analysis using

Gaussian process regression. Computer Methods in

Applied Mechanics and Engineering, 341, 807–826.

https://doi.org/10.1016/J.CMA.2018.07.017

Han, Y., Duan, J., & Wang, S. (2020). Benchmark problems

of hyper-elasticity analysis in evaluation of FEM.

Materials, 13(4), 885.

Jin, J., Feng, S., & Li, S. (2024). Computational Design of

Customized Vacuum-Driven Soft Grippers. IEEE

Robotics and Automation Letters.

Lang, L., Antunes, R., Dutra, T. A., Aguiar, M. L. de,

Pereira, N., & Gaspar, P. D. (2025). Mechanical

Characterization and Computational Analysis of TPU

60A: Integrating Experimental Testing and Simulation

for Performance Optimization. Materials, 18(2).

https://doi.org/10.3390/ma18020240

Liu, S. Q., & Adelson, E. H. (2022). GelSight Fin Ray:

Incorporating Tactile Sensing into a Soft Compliant

Robotic Gripper. http://arxiv.org/abs/2204.07146

Liu, S. Q., Ma, Y., & Adelson, E. H. (2023). GelSight Baby

Fin Ray: A Compact, Compliant, Flexible Finger with

High-Resolution Tactile Sensing.

http://arxiv.org/abs/2303.14883

Maronehitz, P. (2024). Scripting for Mechanical Engineers.

Megan, L., & Croop, B. (2014). A Mechanism for the

Validation of Hyperelastic Materials in ANSYS.

Datapointlabs.

Navez, T., Ménager, E., Chaillou, P., Goury, O.,

Kruszewski, A., & Duriez, C. (2025). Modeling,

Embedded Control and Design of Soft Robots using a

Learned Condensed FEM Model. IEEE Transactions on

Robotics.

Nonaka, T., Abdulali, A., Sirithunge, C., Gilday, K., & Iida,

F. (2023). Soft robotic tactile perception of softer

objects based on learning of spatiotemporal pressure

patterns. 2023 IEEE International Conference on Soft

Robotics, RoboSoft 2023.

https://doi.org/10.1109/ROBOSOFT55895.2023.1012

1950

Ponce, H., Mart\’\inez-Villaseñor, L., & Mayorga-Acosta,

C. (2021). Design of a soft gripper using genetic

algorithms. Computación y Sistemas, 25(4), 835–842.

Shin, J. H., Park, J. G., Kim, D. Il, & Yoon, H. S. (2021). A

Universal Soft Gripper with the Optimized Fin Ray

Finger. International Journal of Precision Engineering

and Manufacturing - Green Technology, 8(3), 889–899.

https://doi.org/10.1007/s40684-021-00348-1

Stella, F., & Hughes, J. (2023). The science of soft robot

design: A review of motivations, methods and enabling

technologies. Frontiers in Robotics and AI, 9, 1059026.

Suder, J., Bobovský, Z., Mlotek, J., Vocetka, M., Oščádal,

P., & Zeman, Z. (2021). Structural optimization method

of a finray finger for the best wrapping of object.

Applied Sciences (Switzerland), 11(9).

https://doi.org/10.3390/app11093858

Xie, Y., Pinskier, J., Liow, L., Howard, D., & Iida, F.

(2024). A’MAP’to find high-performing soft robot

designs: Traversing complex design spaces using

MAP-elites and Topology Optimization. 2024

IEEE/RSJ International Conference on Intelligent

Robots and Systems (IROS), 11408–11415.

Xie, Y., Wang, X., Iida, F., & Howard, D. (2024). Fin-QD:

A Computational Design Framework for Soft Grippers:

Integrating MAP-Elites and High-fidelity FEM. 2024

IEEE 7th International Conference on Soft Robotics,

RoboSoft 2024, 692–697.

https://doi.org/10.1109/ROBOSOFT60065.2024.1052

1959.

Yi, S., Bai, X., Singh, A., Ye, J., Tolley, M. T., & Wang, X.

(2025). Co-Design of Soft Gripper with Neural Physics.

ArXiv Preprint ArXiv:2505.20404.

Zhang, C., Zhu, P., Lin, Y., Jiao, Z., & Zou, J. (2020).

Modular soft robotics: Modular units, connection

mechanisms, and applications. Advanced Intelligent

Systems, 2(6), 1900166.

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

584