Evaluating Process Parameter Interdependencies

Based on Knowledge Graphs in Manufacturing

Tom Jeleniewski

1 a

, Aljosha K

ocher

1 b

, Hamied Nabizada

1 c

, Jonathan Reif

1 d

Felix Gehlhoff

1 e

and Alexander Fay

2 f

Institute of Automation Technology, Helmut Schmidt University, Holstenhofweg 85, Hamburg, Germany

Chair of Automation, Ruhr University Bochum, Universit

atsstraße 150, Bochum, Germany

Keywords:

Process Parameter Interdependencies, Data Elements, Semantic Web, Ontologies, Web Ontology Language,

OWL, Industry 4.0.

Abstract:

Formal representations of parameter interdependencies are critical for enabling model-based analysis and rea-

soning in manufacturing process knowledge graphs. While ontologies based on industrial standards allow for

structured semantic descriptions, the computability of embedded mathematical expressions remains a chal-

lenging task. This paper presents a SPARQL-driven evaluation framework capable of interpreting and resolv-

ing process parameter interdependencies within a knowledge graph. The approach supports an evaluation of

nested mathematical expressions, contextual data resolution and computation of process relevant results. The

implementation demonstrates how semantic process models can be used for decision support and process op-

timization tasks.

1 INTRODUCTION

Manufacturing systems are increasingly shaped by

demands for individualization, shortened product life

cycles, and reduced lot sizes (Jarvenp

a et al., 2016).

To cope with these dynamics, modern production en-

vironments must be designed for ﬂexibility and re-

conﬁgurability, allowing them to respond to chang-

ing technical and organizational requirements (Afa-

zov, 2013). At the same time, the resulting produc-

tion processes and system architectures become more

complex, both structurally and functionally (L

uder

and Schmidt, 2017).

In this context, Digital Twins (DTs) have become

a key concept for managing complexity and enabling

data-driven decision making in engineering. They

represent assets by digitally capturing their proper-

ties and behavior by means of models, information,

and data (Stark et al., 2017). Especially in process

design and redesign tasks, an essential part of such

https://orcid.org/0009-0007-0360-4108

https://orcid.org/0000-0002-7228-8387

https://orcid.org/0000-0001-8251-837X

https://orcid.org/0009-0001-2079-8967

https://orcid.org/0000-0002-8383-5323

https://orcid.org/0000-0002-1922-654X

DT models consists of quantiﬁable parameter interde-

pendencies that capture the cause-effect relations gov-

erning system behavior (e.g., how cycle time depends

on machine speed and part complexity). Accurately

representing and evaluating these interdependencies

is crucial for tasks such as process optimization, per-

formance estimation, and feasibility assessments.

Semantic Web technologies, such as Resource De-

scription Framework (RDF), offer a means to for-

mally describe such interdependencies in a machine-

interpretable way in order to test different parame-

ter, material, and resource combinations (Gill et al.,

2022).

However, while the Semantic Web provides pow-

erful mechanisms for describing and querying struc-

tural information, support for quantitative reason-

ing and mathematical calculations remains lim-

ited (Sabou et al., 2020). This becomes a limiting

factor in engineering contexts where numeric com-

putations are essential, for example in process opti-

mization, performance estimation, or the evaluation

of physical constraints (Hildebrandt et al., 2017).

Embedding mathematical expressions in the

knowledge graph keeps formulas bound to their

process context and preserves their machine-

interpretable semantics. This enables automated

evaluation of parameter interdependencies and ad-

Jeleniewski, T., Köcher, A., Nabizada, H., Reif, J., Gehlhoff, F. and Fay, A.

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing.

DOI: 10.5220/0013937100004000

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2025) - Volume 2: KEOD and KMIS, pages

86-96

ISBN: 978-989-758-769-6; ISSN: 2184-3228

vanced reasoning such as context-aware retrieval and

consistency checks.

Efforts such as OpenMath-RDF (Wenzel, 2021)

have extended the modeling capabilities of RDF to in-

clude mathematical constructs, providing the founda-

tion for representing formulas and interdependencies

within knowledge graphs.

Our previous work has demonstrated how pro-

cess knowledge and parameter interdependencies

can be semantically modeled using OpenMath ex-

pressions, linked to process ontologies according

VDI/VDE 3682 and data elements according to

DIN EN 61360 (Jeleniewski et al., 2023a). These

expressions capture domain-speciﬁc dependencies,

physical laws, and engineering logic that inﬂuence the

behavior of production systems.

This paper presents a semantic evaluation frame-

work that enables the operational use of interdepen-

dency descriptions within manufacturing knowledge

graphs. The approach uses SPARQL Protocol and

RDF Query Language (SPARQL) queries to extract

and interpret formalized mathematical expressions in

OpenMath-RDF format as well as relevant parameter

data embedded in the graph. This semantic evaluation

prepares the information required for numeric compu-

tation by traversing the symbolic structure, resolving

variable bindings. The resulting expression is then

passed to an external symbolic math engine for ﬁnal

calculation. By doing so, it enables the application

of interdependency knowledge to support automated

calculations in engineering workﬂows.

The remainder of this paper is structured as fol-

lows. Section 2 provides an overview of existing re-

search on modeling and evaluating parameter inter-

dependencies. Section 3 provides an explanation of

the semantic integration of process and parameter de-

scriptions together with interdependencies as mathe-

matical expressions, which is the basis for the evalu-

ation framework. Section 4 presents the implementa-

tion of the SPARQL-driven evaluation framework for

knowledge-based computation of process characteris-

tics together with an industrially motivated scenario.

Finally, Section 5 concludes the paper and outlines

future research directions.

2 RELATED WORK

Early works address parameter interdependencies pri-

marily in the context of simulation-supported process

planning and optimization. (Denkena et al., 2011)

and (Denkena et al., 2012) present methods for di-

mensioning and optimizing process chains based on

mathematical models. These contributions demon-

strate the potential of simulation models to capture

process behavior and support decision-making. How-

ever, the models lack semantic annotations that would

enable reuse, interoperability, or formal reasoning.

A more generalized modeling strategy is proposed

in (Grigoriev et al., 2013), who identiﬁes and formal-

izes key process parameters within the aerospace do-

main and develops a conﬁgurable process model cal-

ibrated with statistical and empirical data. While the

model supports quantitative analysis, it does not inte-

grate standardized semantics.

Other contributions focus on qualitative or de-

scriptive representations of dependencies. (Hoang

et al., 2017) introduce a framework for modeling the

mutual inﬂuence between product, process, and re-

source parameters to support system adaptation in

mechatronic contexts. The method allows engineers

to trace cause-effect relations and deduce necessary

compensations in process or resource conﬁgurations.

However, the approach does not allow for quantita-

tive interdependency modeling and does not support

automated evaluation or inference.

(Albers et al., 2019) take a design-centric perspec-

tive by linking product design features to manufac-

turing process impacts via a multidimensional matrix

representation. This provides engineers with insights

into systemic effects of design changes, but again

lacks formal semantics or machine-interpretable

logic.

To overcome the described limitations, semantic

approaches based on ontologies have been widely ex-

plored. Ontologies provide a mechanism to formally

describe domain knowledge in a reusable, extensible,

and interoperable way.

(Liang, 2018) developed an ontology for pro-

cess planning in additive layer manufacturing, which

structures domain-speciﬁc knowledge around man-

ufacturing steps, machine setups, and material us-

age. (Cheng et al., 2016) combine multiple ontolo-

gies to model devices, products, and parameters for

production lines in an Industry 4.0 context. Both

works demonstrate ontology-based modeling capabil-

ities but remain isolated in scope and do not follow

industrial standardized terminologies. Consequently,

their reuse potential across domains or systems is lim-

ited and interdependencies between parameters are

not modeled explicitly.

A more structured approach is presented

by (Hildebrandt et al., 2020), who outline a

methodology for developing industrial ontologies in

collaboration with domain experts using standardized

terminologies. The method emphasizes the use

of Ontology Design Patterns (ODPs) aligned with

established standards such as VDI/VDE 3682 for

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing

process modeling and DIN EN 61360 for parameter

description. This ensures syntactic and semantic

interoperability and lays the foundation for linked

knowledge representations.

ODPs based on industrial standards have since

been applied in various domains. For exam-

ple, (K

ocher et al., 2020) employ them to model ca-

pabilities and skills of Cyber-Physical System (CPS).

(Gill and Fay, 2023) apply an alignment ontology

based on widely accepted standards to describe air-

craft maintenance processes, showing the generaliz-

ability and applicability of the usage of ODPs. An

important aspect of modeling interdependencies is the

formal representation of mathematical expressions in

a way that is compatible with Semantic Web technolo-

gies. In this way, the formula and its elements can be

semantically annotated with respect to their role in the

process. However, this is not addressed by the publi-

cations mentioned so far.

Rule-based approaches such as Semantic Web

Rule Language (SWRL) allow rule-based reasoning,

but their mathematical expressiveness is restricted to

basic arithmetic. Extensions like the combination of

SWRL with OpenMath improve coverage (S

anchez-

Maci

an et al., 2007). However, built-in predicates in

triple stores cause vendor lock-in and restrict porta-

bility.

A frequently applied alternative is to use RDF as

a descriptive data layer and implement all mathemat-

ical logic in external applications, such as simulation

tools or dedicated software frameworks (Sabou et al.,

2020). While this option is efﬁcient in terms of com-

putation, it eliminates the semantic binding between

formulas, variables, and process parameter descrip-

tions. As a result, interdependencies lose their explicit

machine-interpretable meaning, preventing advanced

use cases such as consistency veriﬁcation.

(Marchiori, 2003) was among the ﬁrst to propose

embedding mathematical semantics into the Semantic

Web, highlighting metadata linkage and queryability

as major advantages. (Lange, 2013) provides a com-

prehensive comparison of MathML and OpenMath for

expressing mathematical knowledge, with a focus on

their integrability into RDF-based systems.

MathML supports the layout and structure of

mathematical formulas, while OpenMath centers on

semantics by referencing operators through standard-

ized Content Dictionaries (CDs)

. (Davenport and

Kohlhase, 2009) argues for the harmonization of

mathematical ontologies and demonstrates the advan-

tages of OpenMath in semantic contexts, particularly

due to its extensible design.

The OpenMath-RDF vocabulary introduced

https://openmath.org/cdnames/

by (Wenzel, 2021) builds on these principles and

allows mathematical expressions to be represented as

RDF graphs. It supports nesting, operator typing, and

the integration of existing OpenMath CDs. Therefore,

(Wenzel, 2021) provides essential infrastructure for

embedding mathematical knowledge into semantic

models.

Building on this foundation, the authors of this

paper have developed an infrastructure that connects

knowledge modeling according to industrial stan-

dards with quantiﬁable interdependencies expressed

as mathematical formulas (Jeleniewski et al., 2023a).

Recent work has shown that embedding formulas in

the ontology supports systematic consistency checks

across process models (Jeleniewski et al., 2025).

However, evaluating such interdependencies within

complex graph structures and preparing them for

computation remains a challenging task, which this

paper aims to address.

3 SEMANTIC MODEL FOR

PROCESS PARAMETER

INTERDEPENDENCIES

To formally represent interdependencies between

process parameters in a reusable and machine-

interpretable manner, we introduced the ParX ontol-

ogy

in (Jeleniewski et al., 2023a). It is implemented

in the Web Ontology Language (OWL) and aligns

structural process knowledge, technical parameter de-

scriptions, and mathematical semantics by integrating

multiple domain-speciﬁc ODPs into a semantically

coherent alignment ontology.

3.1 Ontology Structure and Conceptual

Foundation

The ParX ontology follows a modular design. Each

module reﬂects a domain-speciﬁc conceptualization

and is implemented as an individual TBox ontology.

The alignment ontology imports the respective vo-

cabularies and deﬁnes connecting axioms to combine

them into a uniﬁed ABox-level model.

The following ODPs based on industrial standards

are integrated:

• VDI/VDE 3682

Formalized Process Description

(FPD) for modeling manufacturing processes,

process operators, and state-based input/output

semantics (VDI/VDE 3682:1, 2015),

https://github.com/hsu-aut/parX

https://github.com/hsu-aut/IndustrialStandard-ODP-VDI3682

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

• DIN EN 61360

for the semantic description of

technical parameters including types, instances,

and associated units of measurement (DIN EN

61360-1, 2018),

• UNECE

unit of measurement ontology for

an additional unit speciﬁcation of data ele-

ments (UNECE, 2010),

• VDI/VDE 2206

for a structural description of

technical systems and components (VDI/VDE

2206, 2021),

• OpenMath-RDF

for encoding mathematical ex-

pressions in RDF, including operators, variables,

and functional application structures according

to (Wenzel, 2021).

Each ODP corresponds to a self-contained and

reusable vocabulary rooted in industrial standards.

The ParX alignment ontology acts as a semantic

bridge between them, following best practices for on-

tology integration (Hildebrandt et al., 2020; Gangemi

and Presutti, 2009).

3.2 Process and Parameter Modeling

Process descriptions are formalized by using the

class VDI3682:ProcessOperator, which is re-

sponsible for transforming entities of the super

type VDI3682:State from a prior state to a sub-

sequent state. The classes VDI3682:Product,

VDI3682:Information, and VDI3682:Energy are

sub types of VDI3682:State and are used to spec-

ify the state-describing element. A process op-

erator is assigned to a corresponding resource via

VDI3682:isAssignedTo, pointing to an instance of

VDI3682:TechnicalResource, which is responsible

to perform the process step.

To model parameter semantics, the class

DINEN61360:DataElement is used. Each data

element is linked to:

• a DINEN61360:TypeDescription that provides

semantic annotations, including the expected

UNECE:Unit,

• and a DINEN61360:InstanceDescription,

which holds, for example, actual values.

Units are modeled as individuals of the

UNECE:Unit vocabulary, ensuring syntactic va-

lidity and semantic comparability of data elements

across the graph.

https://github.com/hsu-aut/IndustrialStandard-ODP-DINEN61360

https://github.com/hsu-aut/IndustrialStandard-ODP-UNECE-UoM

https://github.com/hsu-aut/IndustrialStandard-ODP-VDI2206

https://openmath.org/om-rdf/

3.3 Representation of

Interdependencies

Interdependencies between process parameters

are expressed as mathematical relations us-

ing the OpenMath-RDF vocabulary (Wenzel,

2021). Each formula is modeled as an instance of

OM:Application, which references an OM:Operator

(e.g., arith1:divide) and a list of arguments mod-

eled as RDF collections (rdf:List). The ordered

nature of these list structures, using rdf:first and

rdf:rest predicates, ensures deterministic traversal

of mathematical arguments, maintaining the correct

sequence for non-commutative operations. Argu-

ments can be constants, variables or sub-applications,

which in turn are expressed as OM:Application.

Each variable is an instance of

OM:Variable and is semantically linked to a

DINEN61360:DataElement via the object property

ParX:isDataFor. This creates a clear and machine-

interpretable binding between symbolic mathematical

constructs and domain-speciﬁc process data.

The ParX alignment ontology deﬁnes the seman-

tic relations that integrate process structure, parameter

data, and mathematical logic across the involved vo-

cabularies. It introduces dedicated object properties

to enable these cross-domain associations. A class di-

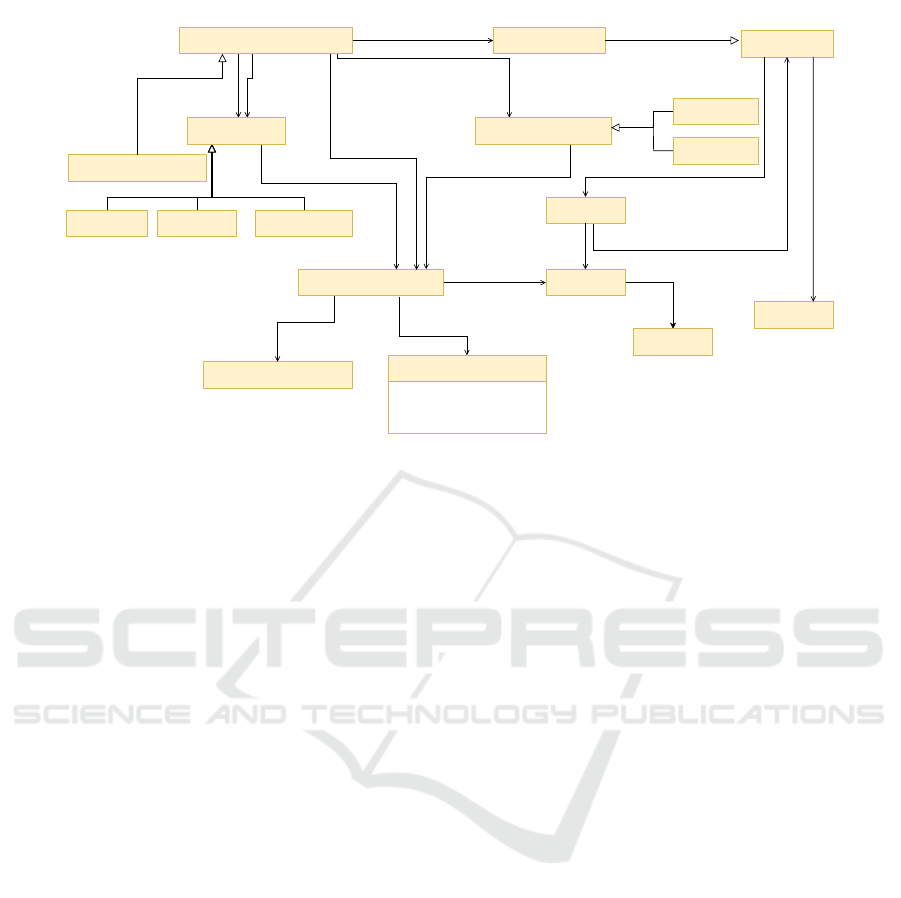
agram of this ontology is illustrated in Figure 1.

The property ParX:isDataFor asso-

ciates mathematical variables with corre-

sponding parameter instances, represented as

DINEN61360:DataElement individuals. To as-

sociate a mathematical expression with a speciﬁc

process step, ParX:hasInterdependency is

used to assign an OM:Application instance to

a VDI3682:ProcessOperator. Furthermore,

ParX:expectsUnit declares the expected unit

for each OM:Variable, enabling unit consistency

veriﬁcation during evaluation and integration.

3.4 Decomposition and Composition of

Interdependencies

In complex manufacturing systems, it is often not fea-

sible to specify a comprehensive interdependency for-

mula for an entire process operator, especially when

process knowledge is distributed across multiple en-

gineering domains or abstraction levels. For example,

a manufacturing process may span multiple depart-

ments, with specialized teams using entirely different

technologies. As each process technology relies on

distinct domain expertise, formalizing interdependen-

cies across the entire process chain as a single expres-

sion becomes increasingly challenging.

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing

VDI3682:ProcessOperator

VDI3682:State

VDI3682:hasInput

VDI3682:Product VDI3682:Energy VDI3682:Information

DINEN61360:hasDataElement

DINEN61360:DataElement

OM:Application

OM:Operator

OM:arguments

DINEN61360:TypeDescription

UNECE:Unit

DINEN61360:hasTypeDescription

DINEN61360:hasInstanceDescription

OM:operator

OM:ObjectList

DINEN61360:InstanceDescription

+Value

+ExpressionGoal

+LogicInterpretation

VDI3682:isAssignedTo

DINEN61360:hasDataElement

VDI3682:ProcessOperator

VDI3682:State

VDI3682:TechnicalResource

OM:Variable

ParX:isDataFor

VDI3682:hasOutput

VDI3682:ProcessOperator

VDI3682:State

VDI3682:ProcessOperator

VDI3682:State

DIN8580:ManufacturingProcess

ParX:Interdependency

ParX:hasInterdependency

rdf:first

DINEN61360:hasDataElement

VDI2206:System

VDI2206:Module

UNECE:Unit

ParX:expectsUnit

0..*

1..*1..*

0..*

0..* 1

0..*

0..* 0..*

0..1

0..*

0..*0..*

0..* 0..*

0..*

0..* 0..*

0..*

rdf:first

Figure 1: Class diagram of the ParX alignment ontology illustrating the integration of VDI/VDE 3682, DIN EN 61360 and

OpenMath-RDF ontology design patterns (based on (Jeleniewski et al., 2023a)).

To address this, the ParX ontology supports the

decomposition of high-level process operators into

ﬁner-grained subprocesses, for which interdependen-

cies can be formalized. Conversely, it allows the com-

position of these local expressions into a global inter-

dependency that approximates or represents the be-

havior of the parent process operator.

Interdependency Decomposition: If no interde-

pendency can be deﬁned at a higher level of ab-

straction, the process may be decomposed into sub-

ordinate subprocesses. Following the concept of

VDI/VDE 3682, each of these subprocesses is again

modeled as a VDI3682:ProcessOperator, allow-

ing interdependencies to be speciﬁed at a more de-

tailed level. Each subprocess represents a more spe-

ciﬁc operation or transformation step and may be

linked to its own interdependency expression using

ParX:hasInterdependency. On the level of smaller

functional units, parameter interdependencies are typ-

ically easier to deﬁne and manage due to their reduced

complexity and well contained scope.

Interdependency Composition: If all subpro-

cesses that contribute to a higher-level process are

described with formalized interdependencies, it be-

comes possible to derive an overarching interde-

pendency expression by composing the mathemati-

cal content of the subordinate expressions. This is

achieved by symbolically substituting the outputs of

one subprocess into the inputs of the next.

Through recursive resolution and replacement,

nested formulas can be merged into an evaluable ex-

pression that characterizes the input-output behavior

of the entire composed process.

This approach allows system architects and engi-

neers to work with manageable and validated frag-

ments of process knowledge while enabling auto-

mated reasoning and evaluation at higher abstraction

levels. It supports both top-down modeling (starting

from an abstract speciﬁcation and reﬁning into sub-

processes) and bottom-up synthesis (aggregating de-

tailed subprocess knowledge into a global view).

As a result, the decomposition and composition

mechanisms offer a method to represent and evaluate

parameter interdependencies across process descrip-

tion hierarchies.

3.5 Integration and Instantiation of

Interdependencies

The integration of interdependencies into the ontol-

ogy follows a structured method introduced in (Jele-

niewski et al., 2023b), which enables the systematic

formalization of informal process knowledge and its

instantiation within the semantic model.

Two main types of input are required for this inte-

gration:

• A process model structured according to

VDI/VDE 3682, describing process operators,

their associated inputs, outputs, and assigned

technical resources. Such models can be created

using dedicated modeling tools and transformed

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

ex:TargetTemperature

DIN61360:DataElement

ex:Conﬁguration

VDI3682:Information

ex:Curing

VDI3682:ProcessOperator

ex:ReinforcedPart

VDI3682:Product

ex:InjectedPreform

VDI3682:Product

ex:PreformTemperature

DIN61360:DataElement

ex:CuringTime

VDI3682:Information

ex:t

OM:Variable

ex:TimeDE

DIN61360:DataElement

ex:Time

DIN61360:TypeDescription

UNECE:SEC

ex:Time

ParX:Interdependency

ex:TimeFrac

OM:Application

CD:arith1/divide

OM:Object

CD:relation1/eq

OM:Object

ex:TimeAttribute2

rdf:List

ex:TimeAttribute1

rdf:List

ex:TDiff

OM:Application

CD:arith1/minus

OM:Object

ex:DiffAttribute1

rdf:List

ex:DiffAttribute2

rdf:List

ex:EqualAttribute1

rdf:List

ex:EqualAttribute2

rdf:List

ex:Phi

OM:Variable

ex:TTarget

OM:Variable

ex:TActual

OM:Variable

ex:CuringRate1

VDI3682:Information

ex:Rate

DIN61360:DataElement

ex:Temperature

DIN61360:TypeDescription

UNECE:KEL

ex:HeatRate

DIN61360:TypeDescription

UNECE:F12

DIN61360:hasDataElement

VDI3682:hasInput

ParX:hasInterdependency

OM:operator

OM:arguments

rdf:rest

rdf:first

rdf:rest

rdf:first

rdf:rest

ParX:isDataFor

DIN61360:hasDataElement

VDI3682:hasInput

VDI3682:hasOutput

VDI3682:hasInput

DIN61360:hasTypeDescription

DIN61360:hasDataElement

ParX:expectsUnit

DIN61360:hasTypeDescription

Figure 2: Simpliﬁed excerpt of a curing process step in the ontology, focusing on interdependencies, data element bindings,

and unit semantics.

into OWL, e.g. using the fpb-owl-mapper

which converts JSON-based FPD models gen-

erated via FPB.js

(Nabizada et al., 2020) into

RDF/OWL representations conforming to the

VDI/VDE 3682 ODP.

• A mathematical expression describing the inter-

dependency between input and output parame-

ters, which must be represented in a form that

is compatible with the semantic process and pa-

rameter description model. To ensure this level

of integration, the expression must be encoded

using the OpenMath-RDF format. Since manu-

ally creating OpenMath-RDF structures is techni-

cally demanding, a dedicated parsing tool is pro-

vided: the openmath-rdf-parser

. It allows users

to enter formulas as human-readable strings (e.g.,

F = m · a) and automatically transforms them into

OpenMath-compliant RDF graphs.

Starting with the identiﬁcation of the relevant

VDI3682:ProcessOperator, the process model is

analyzed to collect associated input and output pa-

rameters, as well as any assigned technical resources.

If an interdependency between these parameters is

known, the corresponding mathematical expression

can be integrated in the ontology as OpenMath-RDF.

The involved variables are then aligned to data el-

ements according to the concept described in Sec-

tion 3.3.

If no suitable interdependency is available at the

https://github.com/hsu-aut/fpb-owl-mapper

https://fpbjs.net

https://github.com/aljoshakoecher/openmath-rdf-parser

given abstraction level, the process can be decom-

posed into subprocesses where interdependencies are

known (cf. Section 3.4). Through application of

the integration procedure, these subprocesses are pro-

gressively enriched with interdependency knowledge.

This structured approach enables the construction

of semantically enriched process knowledge graphs

and is explained in more detail in (Jeleniewski et al.,

2023b).

An exemplary graph is shown in Figure 2. The

ﬁgure illustrates a process description that includes

both process parameters and an integrated representa-

tion of interdependencies used to calculate the curing

time of a curing process step (highlighted in black)

as part of the Resin Transfer Molding (RTM) process.

During curing, the already injected preform is trans-

formed into a reinforced product.

To enable this, input information such as the cool-

ing rate and target temperature, as well as the current

temperature of the injected preform, is provided.

The elements of the integrated formula (see (1)),

which represent the interdependencies between cur-

ing time and process parameters (required tempera-

ture T

target

, the actual temperature T

actual

, and the cur-

ing rate φ

cure

) are highlighted by crosshatched nodes

in the graph.

cure

target

− T

actual

cure

(1)

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing

4 INTERDEPENDENCY

EVALUATOR

Understanding and applying parameter interdepen-

dencies in a reliable and reusable manner requires not

only formalized representations of these interdepen-

dencies, but also mechanisms to evaluate them in spe-

ciﬁc process contexts. For this purpose, we propose

an evaluation framework that computes output values

from process models by interpreting mathematical ex-

pressions embedded in the process knowledge graph.

The evaluator is available on GitHub

The approach enables reusable, fully semantic-

based evaluation without requiring external scripts for

formula implementations.

A key design decision is the complete reliance

on SPARQL queries for traversing and resolving

the mathematical expressions encoded in OpenMath-

RDF. By leveraging the queryable graph structure,

the evaluator avoids manual evaluation routines (e.g.,

identifying applicable formulas, collecting relevant

parameter or data values and manual execution of

calculations). Instead, the logical structure of the

OpenMath-RDF model itself guides the evaluation

and ﬁnally, the computation of interdependency de-

scriptions.

4.1 Workﬂow and Implementation

The evaluation framework enables the evaluation of

formally described parameter interdependencies by

computing mathematical expressions embedded in

the process knowledge graph. It is implemented as

a Node.js application and interacts with a SPARQL-

compliant triple store as graph database, where se-

mantic process models and parameter data are hosted.

The evaluation process follows a structured multi-

stage workﬂow, which is guided by SPARQL queries.

Each stage incrementally resolves the symbolic ex-

pressions and integrates instance data from the graph

to obtain a ﬁnal numerical result. In Figure 3, the

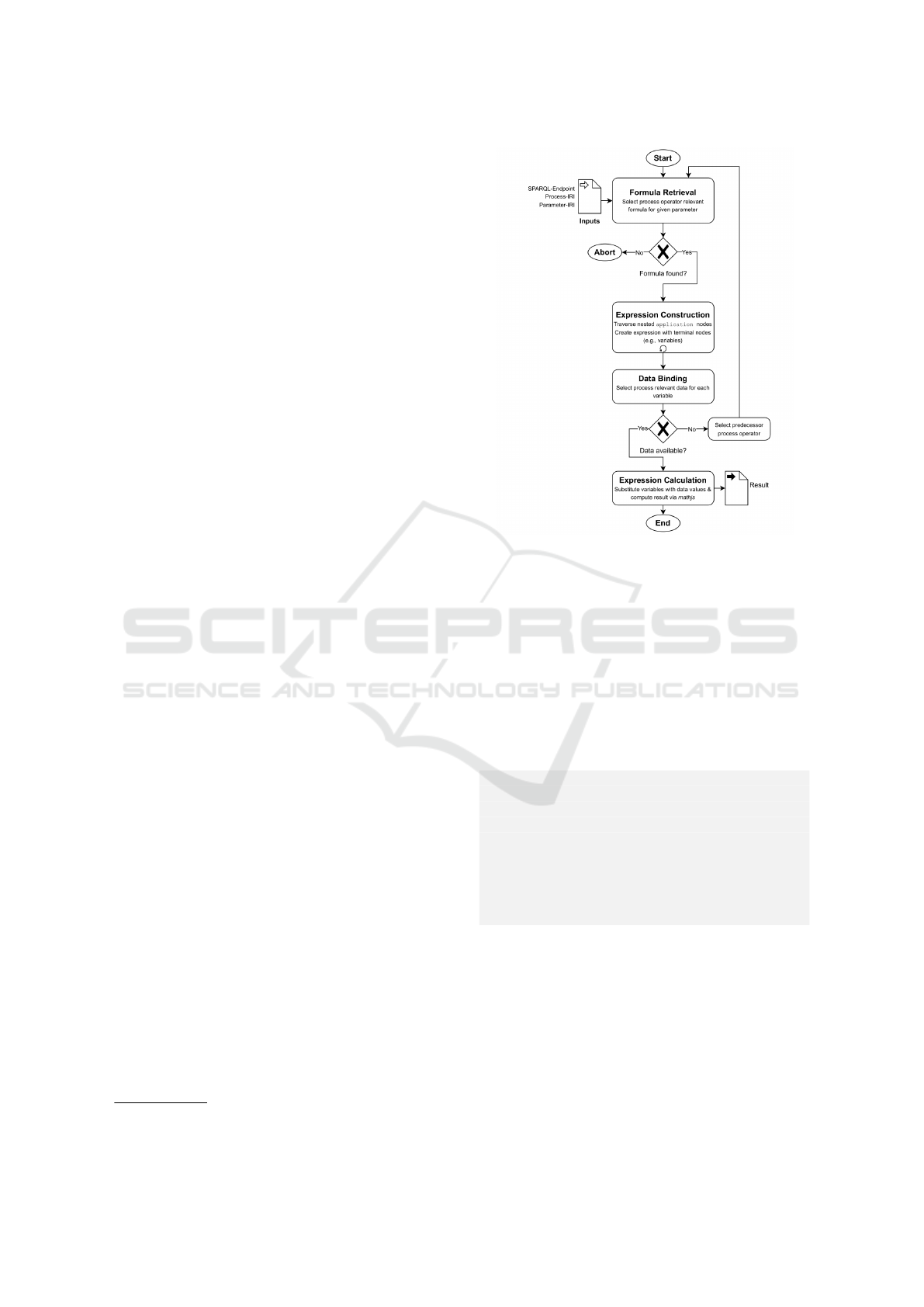
workﬂow performed by the framework is illustrated.

Formula Retrieval: The evaluation workﬂow be-

gins by identifying the mathematical expression that

deﬁnes a speciﬁc output parameter for a given

VDI3682:ProcessOperator. This is achieved

through a SPARQL query that selects expressions as-

sociated via the ParX:hasInterdependency relation

and additionally checks whether the expression repre-

sents an equality, indicated by the om:operator be-

ing CD:relation1/eq (see Listing 1).

https://github.com/jelenito/ParX-evaluator

Figure 3: Workﬂow performed by the evaluation frame-

work.

The query then navigates to the left-hand side of

the equality (ﬁrst element of the rdf:List of argu-

ments) and veriﬁes that it is a variable assigned to the

target parameter (DINEN61360:DataElement) using

the ParX:isDataFor property. This ensures that only

those expressions are retrieved in which the speciﬁed

parameter is explicitly deﬁned as the variable being

solved for.

Listing 1: SPARQL-based formula retrieval.

SELECT ? fo rmu la WHERE {

<${ pr oc es s U r i }>

parx : ha s I n te rd e p e nd e n c y ? f or m ul a .

? f or mul a om : ar gu m en ts ? ar g Li s t ;

om : op e ra to r CD : r el at io n 1 / eq .

? a rg Lis t rdf : f i rst ? LHS .

? LHS a om : Va ri a bl e .

? de parx : i sD at a F o r ? LHS .

FILTER( s tr (? de ) = "${ da t a E l e m e nt Ir i } "

)}

Expression Construction: Once the correspond-

ing formula has been retrieved, the evaluator con-

structs a symbolic representation of the expression

by recursively traversing OM:Application nodes via

SPARQL queries. Each application node speciﬁes a

mathematical operator via a reference to a OpenMath

CD and a set of arguments encoded as RDF lists.

The evaluator follows these references and expands

the expression tree by recursively resolving each ar-

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

gument. This process continues until all branches

of the expression reduce to terminal nodes (such as

OM:Variable), which represent the leaves of the tree.

The resulting symbolic tree accurately reﬂects the hi-

erarchical structure of the mathematical expression

and forms the basis for subsequent variable substitu-

tion.

Data Binding: Each OM:Variable in the expres-

sion is assigned to a DINEN61360:DataElement via

ParX:isDataFor. The evaluator queries the associ-

ated DINEN61360:InstanceDescription to retrieve

available numerical values. These are substituted into

the expression tree, forming the basis for further sym-

bolic evaluation.

Recursive Fallback Resolution. A particular chal-

lenge addressed by the framework is the recursive

resolution of missing data values. If no directly as-

signed data element provides a value for a required

variable, the evaluator identiﬁes preceding formulas

that compute the corresponding data element as an

output. Evaluation is then recursively triggered for

these upstream processes, allowing multi-step depen-

dencies to be resolved without external orchestration

logic.

Expression Calculation: The evaluator distin-

guishes between semantic graph traversal and sym-

bolic computation. While SPARQL provides basic

query and arithmetic functionality, it lacks mecha-

nisms for symbolic evaluation, dynamic recursion, or

expression tree manipulation (Graux et al., 2020).

Hence, only graph access and structural analy-

sis are handled via SPARQL, whereas mathemati-

cal processing is delegated to mathjs. mathjs

a well documented open-source mathematics library

for JavaScript that supports symbolic parsing and nu-

meric computation of mathematical expressions.

Once all variables are resolved, the symbolic

expression is converted into the required mathjs

format and passed to the mathjs engine for ﬁnal

evaluation. mathjs engine parses and computes the

result based on the deﬁned mathematical operators

and numeric inputs.

The framework can be integrated as a component

into broader engineering environments or knowledge-

based systems. Its architecture provides a maintain-

able and extensible foundation for future capabilities

such as constraint checking, explanation facilities, or

domain-speciﬁc evaluation logic.

https://mathjs.org/

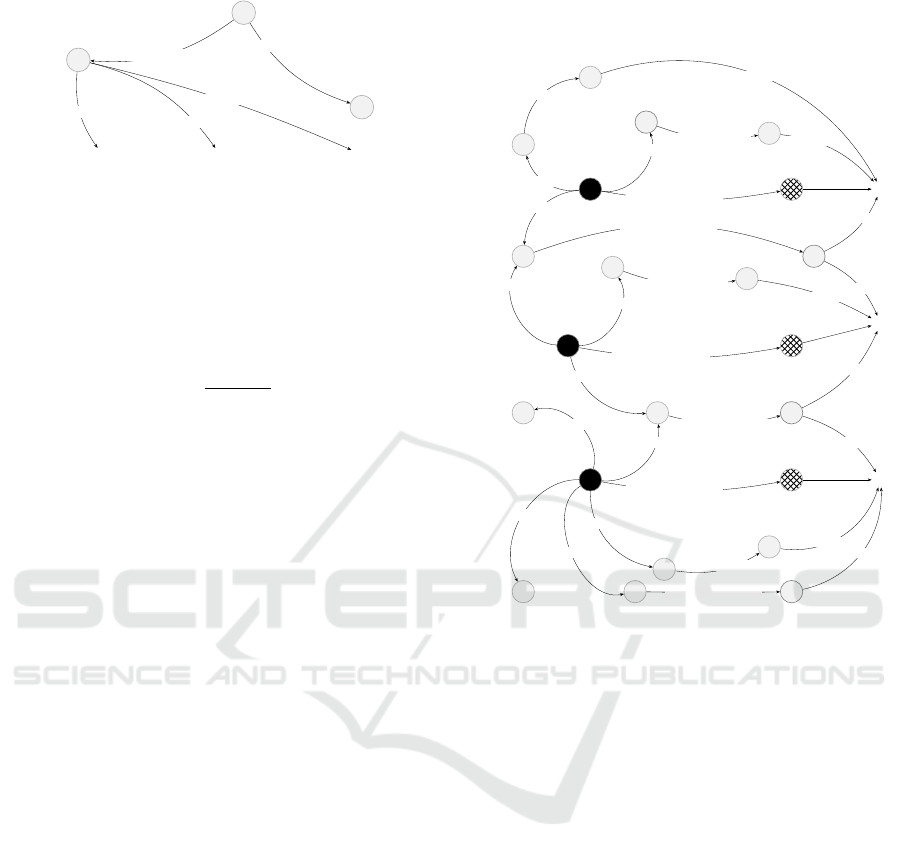
4.2 Application Example: RTM Process

In cooperation with an industrial partner from the

ﬁeld of composite manufacturing for aerospace com-

ponents, a simpliﬁed example of an RTM process has

been modeled. The scenario represents a condensed

and illustrative segment of a process chain (see Fig-

ure 5), used to demonstrate the capabilities of the pro-

posed evaluation framework. To ensure clarity and fo-

cus, only a selected subset of interdependencies and

process operators is considered in this example.

RTM is a widely used closed-mold process for

manufacturing ﬁber-reinforced plastic components.

In this process, dry ﬁber preforms are placed into a

mold cavity, and a thermoset resin is injected to in-

ﬁltrate the ﬁbers. Once the mold is ﬁlled, curing is

initiated to solidify the composite structure. Process

performance depends on geometric, material, and in-

jection parameters, which exhibit various interdepen-

dencies that can be formalized and evaluated.

The selected example comprises three consec-

utive VDI3682:ProcessOperator instances, each

connected via data elements and mathematical ex-

pressions modeled using OpenMath-RDF. For im-

proved readability, the full formulas, which are de-

scribed in this section, are omitted in Figure 5

and are instead indicated after the instances of

ParX:Interdependency (crosshatched nodes). An

exemplary connection of variables within a formula

including assigned data elements can be seen in Fig-

ure 2.

Tool Setup. The ﬁrst process operator deter-

mines the required resin volume based on geo-

metric properties of the component and the tool.

The VDI3682:TechnicalResource RTM-Tool pro-

vides the mold cavity area A

cav

, and the de-

sired laminate thickness h

lam

is supplied as a

VDI3682:Information input. The output is the con-

ﬁgured Tool annotated with the ﬁlling volume V . The

process operator is aligned to an interdependency de-

scribed by (2).

V = A

cav

· h

lam

(2)

Resin Preparation. The second process operator

describes the resin preparation. The aligned inter-

dependency description describes the resin shot mass

using the computed volume and the material density

res

of the selected resin. The output is a prepared

resin shot with the mass computed by the interdepen-

dency described by (3).

res

= ρ

res

·V (3)

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing

ex:InjectionFlowRate

DIN61360:DataElement

ex:FlowRate

DIN61360:TypeDescription

UNECE:2J

ex:InjectionFlowRate1

DIN61360:InstanceDescription

100

”actual value”

”=”

DIN61360:hasTypeDescription

DIN61360:hasInstanceDescription

DIN61360:value

DIN61360:logicInterpretation

DIN61360:expressionGoal

Figure 4: Examplary data element description for data bind-

ing.

Resin Injection. The third process operator repre-

sents the injection of the resin into the mold. It

takes the resin shot (with mass m

res

) and the injection

ﬂow rate

inj

as input. The injection time t

inj

can be

computed with the aligned interdependency descrip-

tion (see (4)).

inj

res

inj

(4)

This example demonstrates a typical use case

during early-stage process planning, where a user

queries the system for the required injection time t for

a new composite component. The evaluator begins

by identifying the mathematical expression linked

to the injection operator and attempts to resolve all

input variables using the knowledge graph.

In this exemplary use case (ex:ResinInjection),

the ﬂow rate

inj

and resin density ρ

res

are directly

available via linked DINEN61360:DataElement

instances, but the resin shot mass m

res

is not. An ex-

emplary data element assignment for

inj

= 100cm

can be seen in Figure 4. The unit cm

is assigned via

the classiﬁcation as UNECE:2J.

To resolve this missing value, the eval-

uator recursively identiﬁes the preceding

ex:ResinPreparation operator, retrieves its

associated expression, and checks whether its inputs

are available via SPARQL querying.

Again, the resin volume V required to calcu-

late m

res

is not directly given. Thus, the evaluator

continues to the ex:ToolSetup operator and resolves

the volume expression using the cavity area A

cav

and

laminate thickness h

lam

, both of which are connected

to data elements within the technical resource and in-

put information.

Once V is calculated, it is passed upstream to com-

pute m

res

, which in turn enables the evaluation of t

inj

Through this recursive traversal, the evaluator derives

the requested output value solely from the available

data for A

cav

, h

lam

, ρ

res

, and

inj

This illustrates how the proposed framework en-

ables dynamic resolution and stepwise evaluation of

parameter interdependencies within process models,

supporting transparency, reusability, and automated

decision-making.

ex:ToolSetup

VDI3682:ProcessOperator

ex:VolumeCalc

ParX:Interdependency

[...]

ex:ResinPreparation

VDI3682:ProcessOperator

ex:MassCalc

ParX:Interdependency

[...]

ex:ResinInjection

VDI3682:ProcessOperator

ex:TimeCalc

ParX:Interdependency

[...]

ex:InjectionParam

VDI3682:Information

ex:InjectionFlowRate

DIN61360:DataElement

ex:Order

VDI3682:Information

ex:Height

DIN61360:DataElement

ex:Area

DIN61360:DataElement

ex:Resin

VDI3682:Product

ex:Density

DIN61360:DataElement

ex:RTM-Tool

VDI3682:TechnicalResource

ex:ToolConﬁguration

VDI3682:Information

ex:ResinShot

VDI3682:Product

ex:Mass

DIN61360:DataElement

ex:Volume

DIN61360:DataElement

ex:InjectionPerformance

VDI3682:Information

ex:InjectionTime

DIN61360:DataElement

ex:Preform

VDI3682:Product

ex:InjectedPreform

VDI3682:Product

VDI3682:hasInput

VDI3682:isAssignedZTo

VDI3682:hasOutput

VDI3682:hasInput

VDI3682:hasOutput

VDI3682:hasInput

VDI3682:hasOutput

ParX:hasInterdependency

DIN61360:hasDataElement

ParX:isDataFor

DIN61360:hasDataElement

Figure 5: Exemplary excerpt of parameter interdependen-

cies across three process operators (black) in an RTM pro-

cess.

5 CONCLUSION AND FUTURE

WORK

This paper presents a semantic modeling and eval-

uation framework for representing process param-

eter interdependencies in manufacturing systems

based on knowledge graphs. The ParX ontol-

ogy integrates structural process descriptions, pa-

rameter semantics, and formalized mathematical ex-

pressions using ODPs derived from industrial stan-

dards such as VDI/VDE 3682, DIN EN 61360,

and OpenMath-RDF. This alignment enables a

machine-interpretable, reusable representation of pro-

cess knowledge, capable of capturing domain-speciﬁc

dependencies in a standardized form.

Building upon this model, a SPARQL-driven eval-

uation framework has been introduced that allows

mathematical interdependencies to be resolved and

computed directly based on the ontology. The ap-

proach separates semantic traversal and symbolic

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

computation by using SPARQL queries for graph nav-

igation and delegating the mathematical evaluation to

an external computation engine. This architecture al-

lows for ﬂexible evaluation workﬂows and supports

recursive resolution of upstream dependencies along

process chains.

The framework enables automated parameter

evaluation, can support design-time decision support,

and offers a mechanism to evaluate interdependencies

across multiple levels of process abstraction. The pro-

posed approach demonstrates how semantic technolo-

gies can be extended beyond structural modeling to

actively support quantitative reasoning in manufactur-

ing engineering contexts.

Furthermore, the current evaluation framework

focuses primarily on value calculation. Restriction

checking against predeﬁned constraints during run-

time evaluation has not yet been fully integrated.

As part of future work, the evaluation framework

will be extended to incorporate constraint-based val-

idation mechanisms, allowing computed outputs in-

cluding intermediate results to be automatically ver-

iﬁed against parameter restrictions. This extension

will strengthen the integration between interdepen-

dency evaluation and restriction checking, and sup-

port advanced reasoning capabilities for knowledge-

based process analysis and optimization.

Although the proposed approach has shown no ob-

servable response delays in the presented scenarios,

it must be acknowledged that performance may de-

crease when the number of triples and the complex-

ity of concatenated formulas increase. As SPARQL

query execution time is inherently dependent on

graph size, the scalability remains a limitation and

subject of future work.

To further increase accessibility and practical

adoption, it is also planned to encapsulate the eval-

uation logic into a dedicated software package (e.g.,

an npm module), enabling its seamless reuse and inte-

gration into engineering environments and web-based

tools.

ACKNOWLEDGEMENTS

This contribution originates from the projects LaiLa

and iMOD, funded by dtec.bw – Digitalization and

Technology Research Center of the Bundeswehr

which we gratefully acknowledge. dtec.bw is funded

by the European Union – NextGenerationEU.

REFERENCES

Afazov, S. M. (2013). Modelling and simulation of manu-

facturing process chains. CIRP Journal of Manufac-

turing Science and Technology, 6(1):70–77.

Albers, A., St

urmlinger, T., Mandel, C., Wang, J., de Fru-

tos, M. B., and Behrendt, M. (2019). Identiﬁcation of

potentials in the context of Design for Industry 4.0 and

modelling of interdependencies between product and

production processes. Procedia CIRP, 84:100–105.

Cheng, H., Zeng, P., Xue, L., Shi, Z., Wang, P., and Yu, H.

(2016). Manufacturing Ontology Development Based

on Industry 4.0 Demonstration Production Line. In

2016 Third International Conference on Trustworthy

Systems and their Applications (TSA), pages 42–47.

IEEE.

Davenport, J. H. and Kohlhase, M. (2009). Unifying Math

Ontologies: A Tale of Two Standards. In Carette,

J., Dixon, L., Coen, C. S., and Watt, S. M., editors,

Intelligent Computer Mathematics, volume 5625 of

Lecture Notes in Computer Science, pages 263–278.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Denkena, B., Behrens, B.-A., Charlin, F., and Dannenberg,

M. (2012). Integrative process chain optimization

using a genetic algorithm. Production Engineering,

6(1):29–37.

Denkena, B., Henjes, J., and Henning, H. (2011).

Simulation-based dimensioning of manufacturing

process chains. CIRP Journal of Manufacturing Sci-

ence and Technology, 4(1):9–14.

DIN EN 61360-1 (2018). Standard data element types with

associated classiﬁcation scheme - Part 1: Deﬁnitions -

Principles and methods (IEC 61360-1:2017).

Gangemi, A. and Presutti, V. (2009). Ontology Design Pat-

terns. In Staab, S. and Studer, R., editors, Handbook

on Ontologies, pages 221–243. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

Gill, M. S. and Fay, A. (2023). Utilisation of semantic tech-

nologies for the realisation of data-driven process im-

provements in the maintenance, repair and overhaul of

aircraft components. CEAS Aeronautical Journal.

Gill, M. S., Reif, J., Jeleniewski, T., Weigand, M.,

and Fay, A. (2022). Application potentials of se-

mantic technologies for digital twins in aircraft de-

sign, manufacturing and maintenance. In dtec.bw-

Beitr

age der Helmut-Schmidt-Universit

at / Univer-

sit

at der Bundeswehr Hamburg: Forschungsak-

tivit

aten im Zentrum f

ur Digitalisierungs- und Tech-

nologieforschung der Bundeswehr dtec.bw - Band 1.

Universit

atsbibliothek der HSU/UniBw H.

Graux, D., Sejdiu, G., Stadler, C., Napolitano, G., and

Lehmann, J. (2020). MINDS: A Translator to Embed

Mathematical Expressions Inside SPARQL Queries.

In Blomqvist, E., Groth, P., de Boer, V., Pellegrini,

T., Alam, M., K

afer, T., Kieseberg, P., Kirrane, S.,

Mero

no-Pe

nuela, A., and Pandit, H. J., editors, Se-

mantic Systems. In the Era of Knowledge Graphs,

volume 12378 of Lecture Notes in Computer Sci-

ence, pages 104–117. Springer International Publish-

ing, Cham.

Evaluating Process Parameter Interdependencies Based on Knowledge Graphs in Manufacturing

Grigoriev, S. N., Kutin, A. A., and Turkin, M. V.

(2013). Modelling Complex Production Processes in

Aerospace Industry based on Dimensional Analysis.

Procedia CIRP, 7:473–478.

Hildebrandt, C., Glawe, M., M

uller, A. W., and Fay, A.

(2017). Reasoning on Engineering Knowledge: Ap-

plications and Desired Features. In Blomqvist, E.,

Maynard, D., Gangemi, A., Hoekstra, R., Hitzler, P.,

and Hartig, O., editors, The Semantic Web, volume

10250 of Lecture Notes in Computer Science, pages

65–78. Springer International Publishing, Cham.

Hildebrandt, C., K

ocher, A., K

ustner, C., Lopez-Enriquez,

C.-M., M

uller, A. W., Caesar, B., Gundlach, C. S.,

and Fay, A. (2020). Ontology Building for Cyber–

Physical Systems: Application in the Manufacturing

Domain. IEEE Transactions on Automation Science

and Engineering, 17(3):1266–1282.

Hoang, X.-L., Marks, P., Weyrich, M., and Fay, A.

(2017). Modeling of interdependencies between prod-

ucts, processes and resources to support the evolu-

tion of mechatronic systems. IFAC-PapersOnLine,

50(1):4348–4353.

Jarvenp

a, E., Siltala, N., and Lanz, M. (2016). Formal

resource and capability descriptions supporting rapid

reconﬁguration of assembly systems. In 2016 IEEE

International Symposium on Assembly and Manufac-

turing (ISAM), pages 120–125. IEEE.

Jeleniewski, T., Nabizada, H., Reif, J., Gehlhoff, F., and

Fay, A. (2025). Consistency Veriﬁcation in Ontology-

Based Process Models with Parameter Interdependen-

cies. In 2025 IEEE 30th International Conference

on Emerging Technologies and Factory Automation

(ETFA), pages 1–8. IEEE.

Jeleniewski, T., Nabizada, H., Reif, J., K

ocher, A., and Fay,

A. (2023a). A Semantic Model to Express Process

Parameters and their Interdependencies in Manufac-

turing. In 2023 IEEE 32nd International Symposium

on Industrial Electronics (ISIE), pages 1–6. IEEE.

Jeleniewski, T., Reif, J., and Fay, A. (2023b). Integrating In-

terdependencies in Semantic Manufacturing Process

Description Models. In 2023 IEEE 28th International

Conference on Emerging Technologies and Factory

Automation (ETFA), pages 1–4. IEEE.

ocher, A., Hildebrandt, C., Vieira da Silva, L. M., and

Fay, A. (2020). A Formal Capability and Skill Model

for Use in Plug and Produce Scenarios. In 2020

25th IEEE International Conference on Emerging

Technologies and Factory Automation (ETFA), pages

1663–1670. IEEE.

Lange, C. (2013). Ontologies and languages for represent-

ing mathematical knowledge on the Semantic Web.

Semantic Web, 4(2):119–158.

Liang, J. S. (2018). An ontology-oriented knowledge

methodology for process planning in additive layer

manufacturing. Robotics and Computer-Integrated

Manufacturing, 53:28–44.

uder, A. and Schmidt, N. (2017). Challenges of Mecha-

tronical Engineering of Production Systems: An Au-

tomation System Engineering View. In Ghezzi, L.,

omberg, D., and Landry, C., editors, Math for the

Digital Factory, volume 27 of Mathematics in Indus-

try, pages 93–114. Springer International Publishing,

Cham.

Marchiori, M. (2003). The Mathematical Semantic Web. In

Asperti, A., Buchberger, B., and Davenport, J. H., ed-

itors, Mathematical Knowledge Management, volume

2594 of Lecture Notes in Computer Science, pages

216–223. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

Nabizada, H., K

ocher, A., Hildebrandt, C., and Fay, A.

(2020). Offenes, webbasiertes Werkzeug zur In-

formationsmodellierung mit Formalisierter Prozess-

beschreibung. In Automation 2020, pages 443–454.

VDI Verlag.

Sabou, M., Bifﬂ, S., Einfalt, A., Krammer, L., Kastner,

W., and Ekaputra, F. J. (2020). Semantics for Cyber-

Physical Systems: A cross-domain perspective. Se-

mantic Web, 11(1):115–124.

anchez-Maci

an, A., Pastor, E., de L

opez Vergara, J. E.,

and L

opez, D. (2007). Extending SWRL to Enhance

Mathematical Support. In Marchiori, M., Pan, J., and

Marie, C., editors, Web Reasoning and Rule Systems,

volume 4524 of Lecture Notes in Computer Science,

pages 358–360. Springer Berlin Heidelberg, Berlin,

Heidelberg.

Stark, R., Kind, S., and Neumeyer, S. (2017). Innovations

in digital modelling for next generation manufacturing

system design. CIRP Annals, 66(1):169–172.

UNECE (2010). Recommendation No. 20: Codes for Units

of Measure Used in International Trade.

VDI/VDE 2206 (2021). Development of mechatronic and

cyber-physical systems.

VDI/VDE 3682:1 (2015). Formalised Process Descriptions

- Concept and Graphic Representation.

Wenzel, K. (2021). OpenMath-RDF: RDF encodings for

OpenMath objects and Content Dictionaries. In 31st

OpenMath Workshop.

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development