Preliminary Design and Control of an Operator-Assistance System

Integrated into a Cobot, for Anatomical Meat-Cutting Process

Alexis Babut

, Chedli Bouzgarrou

, Laurent Sabourin

and Nicolas Bouton

Universit

e Clermont Auvergne, Clermont Auvergne INP, CNRS, Institut Pascal

F-63000 Clermont-Ferrand, France

Keywords:

Operator Assistance System, Collaborative Robot, Compliant Control, Physical Human–Robot Interaction.

Abstract:

This paper presents the preliminary design and control of a collaborative robotic cell for operator assistance

in tasks involving soft material manipulation, such as meat cutting. The system integrates force/torque sen-

sors and employs a Cartesian admittance controller to enable compliant, intuitive physical interaction. The

mechanical design of the end-effector, the control architecture, and the communication strategy are described.

Initial experiments validate the system’s ability to provide stable and responsive assistance in a physical Hu-

man–Robot Interaction (pHRI) context.

1 INTRODUCTION

While automation continues to progress across many

sectors, some manual tasks remain difﬁcult to mecha-

nise due to their complexity, variability and reliance

on human dexterity. This is especially the case in

the meat industry, which faces a labour shortage and

low job attractiveness. Workers are also exposed to

physically demanding conditions, including repetitive

movements, awkward postures and fast-paced work-

ﬂows.

Figure 1: Manual meat-cutting performed by a human op-

erator.

https://orcid.org/0009-0005-2749-1422

https://orcid.org/0000-0003-2394-1770

https://orcid.org/0000-0002-7840-9186

https://orcid.org/0000-0001-5673-5979

Among the various tasks performed in this sec-

tor, anatomical meat cutting is particularly critical and

complex. It requires ﬁne motor skills, adaptability

and force regulation, making it especially resistant

to full automation. To achieve complete mechanisa-

tion, complex physical models would need to be de-

veloped and computed in real time, which remains

a signiﬁcant technological challenge. Consequently,

the choice of an assistance approach using a collabo-

rative robotic system is being considered.

In recent years, collaborative robots (cobots) have

become essential tools in industrial and service ap-

plications requiring physical human-robot interaction

(pHRI). Unlike traditional robots conﬁned to isolated

workspaces, cobots operate alongside humans, requir-

ing advanced strategies to ensure safety, adaptabil-

ity and intuitive control (Farajtabar and Charbonneau,

2024) (Ajoudani et al., 2017).

Tasks involving deformable or soft objects, such

as in meat processing, pose particular challenges for

pHRI due to the unpredictable nature of soft mate-

rials and variable human-applied forces. Conven-

tional position or force control methods often fall

short in achieving both compliant and robust behav-

ior (Keemink et al., 2018).

Impedance and admittance control schemes ad-

dress these challenges by regulating the dynamic in-

teraction between motion and force. Introduced by

Hogan (Hogan, 1984), impedance control is suited to

motion-driven tasks, while admittance control excels

when motion results from external forces, making it

Babut, A., Bouzgarrou, C., Sabourin, L. and Bouton, N.

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process.

DOI: 10.5220/0013928400003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 541-551

ISBN: 978-989-758-770-2; ISSN: 2184-2809

541

especially useful for cooperative scenarios (Keemink

et al., 2018) (Sharkawy and Koustoumpardis, 2022).

During meat-cutting operations, the operator typi-

cally applies signiﬁcant and variable forces on the tool

depending on tissue consistency and cutting direction.

Accurately estimating and responding to these forces

is essential for delivering effective and safe robotic

assistance.

This work presents a Cartesian admittance-based

assistance system integrated into a collaborative

robotic cell. The system is equipped force/torque sen-

sors for estimating user-applied efforts, enabling real-

time compliant motion through a human-centred con-

trol interface.

The remainder of the paper is structured as fol-

lows: Section 2 introduces the robotic cell and tool

design. Section 3 describes the control strategy and

force estimation method. Section 5 presents exper-

imental results, and Section 6 concludes with a dis-

cussion and future directions.

2 OVERVIEW OF THE ROBOTIC

CELL

This section introduces the overall architecture and

key components of the robotic cell. It details the robot

platform, the design of the instrumented tool includ-

ing its sensing capabilities, and the communication

infrastructure that connects all parts of the system.

2.1 System Architecture

The robotic cell is built around a 6-axis UR30 col-

laborative robot (Universal Robots), mounted on a

telescopic pillar (LIFTKIT-UR-620). The UR30 was

selected for its high payload capacity (up to 30 kg)

and compact form factor, which make it particularly

suitable for force-intensive tasks such as meat cut-

ting, where strength, precision and operator safety are

essential. Its collaborative design allows safe inter-

action with human operators, while maintaining the

ﬂexibility required for complex trajectories in con-

strained environments.

The robot is controlled by a real-time Linux-based

computer, and the system integrates sensing, control,

and perception modules to enable accurate tracking

of interactions and responsive behaviour. Communi-

cation between the robot and the control computer is

established through an Ethernet cable.

The robot’s end-effector is equipped with a multi-

sensor instrumented tool, composed of a handle and a

blade, designed for precise interaction measurement.

To perceive the environment, the setup includes a 3D

vision system (StereoLabs Robotics 360 Perception

Kit) and a motion tracking system (Movella MTw

Awinda Research Bundle), which provide real-time

scene analysis and track the human operator’s pose.

These perception systems are not yet employed in the

current study.

Figure 2: Overview of the robotic cell.

2.2 Design of the Instrumented Knife

This part presents the design of the instrumented tool

mounted on the robot’s end-effector, with a focus on

its force/torque sensing capabilities and mechanical

integration. The tool is intended to precisely measure

interaction forces exerted by both the operator and the

manipulated object.

2.2.1 Sensor Integration Prototypes

Force/torque sensors are integrated within the tool as-

sembly to accurately capture interaction forces. The

primary sensor employed is the BOTA Systems Sen-

sONE T15, selected for its high measurement preci-

sion and reliable communication performance. This

sensor measures all forces applied to the mounted tool

and provides better accuracy than the robot’s internal

force/torque sensor.

A custom mechanical adapter was designed to

connect the SensONE sensor to the UR30 robot’s

tool ﬂange. This adapter is manufactured using

Fused Deposition Modelling (FDM) with carbon-

ﬁbre-reinforced Nylon (PA-CF), combining strength

and lightweight properties.

Because two distinct forces act on the tool, the

force applied by the human operator and the reac-

tion force from the product, using only one sensor

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

542

Figure 3: BOTA Systems SensONE T15 force/torque sen-

sor.

(a) Sensor side (b) Robot side

Figure 4: SensONE to UR30 adapter.

will capture their combined effect without distinction.

Therefore, a second force/torque sensor, the BOTA

Systems Medusa, is required to independently mea-

sure and separate these forces.

Figure 5: Forces applied on the tool during a meat-cutting

task with a robot.

Figure 6: BOTA Systems Medusa force/torque sensor.

The Medusa sensor is mounted using a dedicated

adapter, also printed in PA-CF using FDM. A modular

design enables different assembly conﬁgurations, al-

lowing the measurement of forces at either the handle

or the blade.

(a) Top view (b) Bottom view

Figure 7: Second force/torque sensor adapter.

2.2.2 Knife Prototypes

The knife handle was modelled from a 3D scan of a

real industrial knife, commonly used in meat process-

ing. This scan served as a realistic basis for designing

functional handle prototypes, which were manufac-

tured using PLA ﬁlament through FDM (Fused De-

position Modeling) 3D printing.

Figure 8: Industrial knife used as design reference.

To ensure mechanical robustness, the PLA handle

is mounted on a welded steel substructure that serves

as the structural backbone of the tool. This interface

guarantees stability during high-force interactions.

(a) Steel connector (b) Assembled handle

Figure 9: Knife handle of the tool prototypes.

A push-button is integrated into the handle and

connected to an analogue input on the UR30 control

box. This button allows the operator to manually trig-

ger the robot’s compliant motion, offering intuitive in-

teraction during collaborative tasks.

Finally, the complete assembly is mounted using

a tool changer on the robot ﬂange, as shown in Figure

10.

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process

543

Figure 10: Tool assembly mounted on the robot tool ﬂange.

2.3 Communication Setup

The robotic cell relies on a real-time communica-

tion architecture linking the control unit to all sen-

sors and actuators. The UR30 robot communicates

with the control computer through an Ethernet (RJ45)

connection using the TCP/IP protocol. The BOTA

Systems force/torque sensors, including the SensONE

and Medusa models, operate over the EtherCAT pro-

tocol. They are powered using Power-over-Ethernet

(PoE), and sensor data is transmitted to the computer

through the LAN output of the PoE injector.

The 3D vision system is connected to the con-

trol computer through Ethernet using the TCP/IP pro-

tocol. The motion tracking system (Xsens Awinda)

communicates with the computer through a dedicated

USB interface using a virtual COM port (serial pro-

tocol). The tool changer is electrically linked to

the robot’s tool ﬂange I/O, while the telescopic pil-

lar is connected to the control box USB port. Both

are monitored in the ROS2 environment through the

/robot

states topic.

3 CONTROL STRATEGY

This section presents the control strategy developed

for the robotic cell. Due to the limitations of the

Universal Robot interface, control commands are re-

stricted to joint positions or joint velocities. There-

fore, implementing a torque-based control scheme is

not possible, and the control architecture must be de-

signed to accommodate these constraints.

The main objective is to achieve smooth and trans-

parent interaction between the human and the robot in

all directions, including rotation. The robot must re-

Figure 11: Communication architecture of the robotic cell.

spond naturally to the operator’s guidance, allowing

for intuitive and safe cooperation throughout shared

tasks.

In addition to enabling compliant motion, it is nec-

essary to regulate the cutting force applied by the tool.

The control system must implement a force ampliﬁca-

tion strategy, where the cutting force in the task frame

is saturated as F

task

cut

= k ·F

int

3.1 Overview of Admittance Control

The aim of compliant control is to generate the robot’s

movement by emulating a mass-spring-damper sys-

tem behaviour (Keemink et al., 2018) as illustrated in

Figure 13.

Admittance control computes the robot’s displace-

ment x

∈ R

in response to external forces F

ext

∈

, where m = 6 in our case, corresponding to Carte-

sian space. This relationship is modelled using a

mass–spring–damper system equation:

(

−

) + D

(

−

)

− x

) = F

ext

(1)

Here, M

, D

, and K

are the desired Cartesian

inertia, damping, and stiffness matrices respectively,

while x

, and

denote the desired Cartesian tra-

jectory position, velocity, and acceleration.

Using equation 1, the Cartesian acceleration re-

sulting from the applied external forces can be ex-

pressed as:

+ M

−1

ext

− D

(

−

)

−K

− x

)

(2)

After double integration, the resulting Cartesian

position error e

= x

− x

is tracked by a joint-level

control loop, typically handled by the robot’s internal

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

544

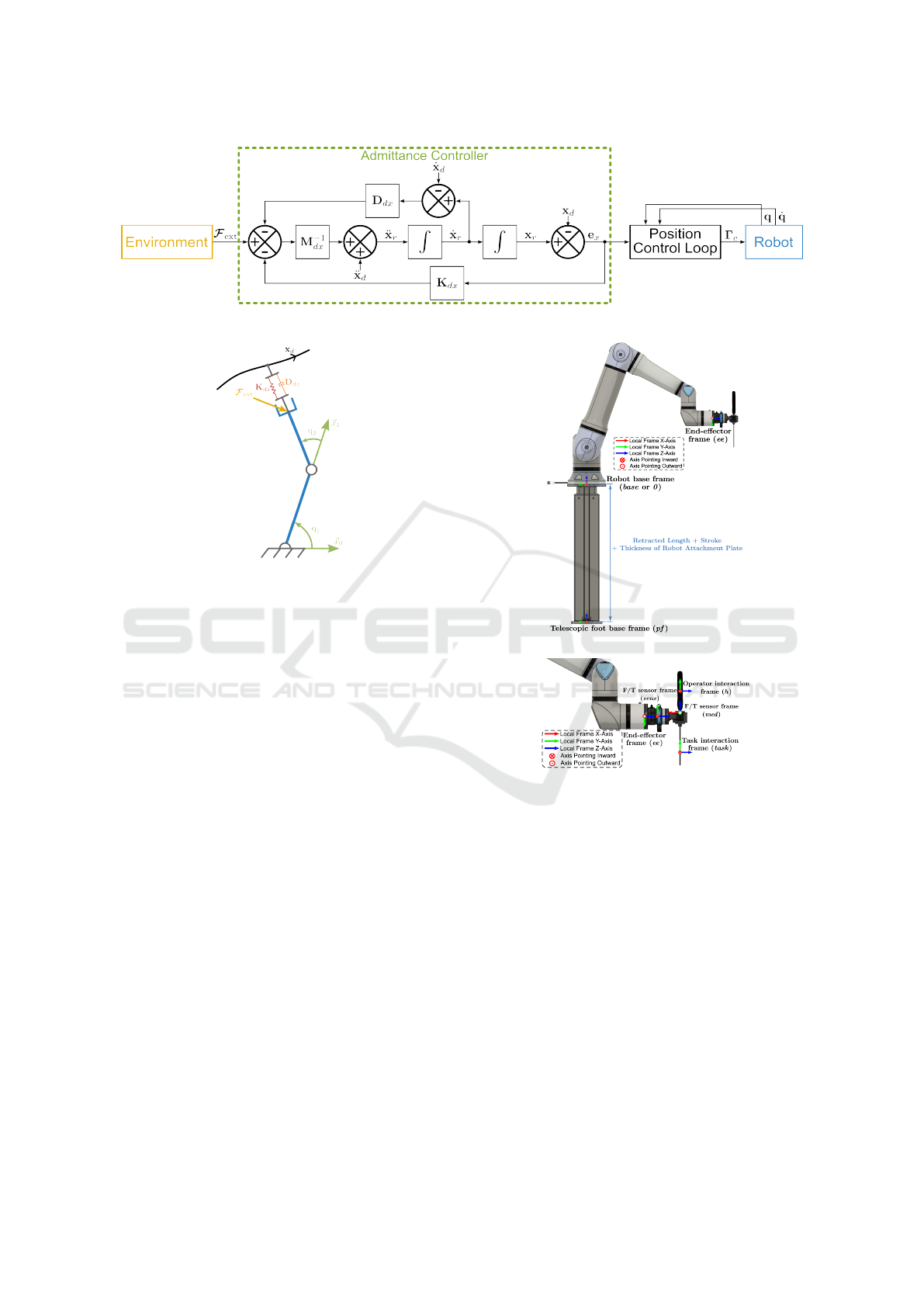
Figure 12: Block diagram of Cartesian admittance control.

Figure 13: Schematic of the robot’s compliant model prin-

ciple.

controller. If the robot’s dynamics are known, an in-

verse dynamics model combined with a feedback con-

troller (such as PID or PD) can be used to regulate the

joint motion and follow the reference trajectory. The

resulting control torques Γ

are applied to the robot’s

actuators, as illustrated in Figure 12.

3.2 System Coordinate Frames

Accurate control and interpretation of sensor data re-

quire a deﬁned set of coordinate frames for the robot,

the tool, and the associated sensors. These frames

serve as spatial references for motion planning, force

estimation, and control execution. Figure 14 shows an

overview of the coordinate frames of the robotic sys-

tem, including the robot base frame, individual joint

frames, and the end-effector frame.

3.3 Estimation of Human-Applied

Forces

To estimate the forces applied by the human operator

on the handle, a six-axis force/torque sensor (Medusa)

is mounted directly on the handle. This sensor mea-

sures the interaction forces transmitted through the

handle. The method presented here is used to iden-

tify the sensor bias and recover the true force exerted

by the operator. The same procedure is applied to

(a) Overview of robotic system

(b) Robot end-effector and tool

Figure 14: Coordinate frames deﬁned for the Robotic sys-

tem.

the primary force/torque sensor (SensONE), which is

mounted on the robot tool ﬂange thanks to an adapter

piece, to estimate external forces acting on the tool.

3.3.1 Bias and Handle Parameter Identiﬁcation

Force/torque sensors typically have intrinsic bias,

causing non-zero output even when no external load

is applied. This bias can result from installation

preloads, component weight, or dynamic effects dur-

ing motion.

Under static conditions without external contact

forces, the sensor output mainly reﬂects the bias and

the gravitational force due to the handle’s mass. The

handle’s mass m

is measured beforehand using a

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process

545

precision scale and then introduced in the identiﬁca-

tion process. The sensor output is modelled as:

med

measured

= f

med

bias

+ m

med

measured

= τ

med

bias

− m

med

CoM

× g

med

(3)

Here, f

med

bias

and τ

med

bias

denote the constant force and

torque sensor biases, m

is the mass of the handle,

and

med

CoM

is the position vector from the sensor

origin to the handle’s centre of mass, expressed in the

sensor frame, as illustrated in Figure 15. The vec-

tor g

med

represents the gravity vector expressed in the

sensor frame, computed from the gravity vector in the

robot base frame:

base



0 0 −9.81



m/s

Given

med

as the rotation matrix of the sensor

relatively to the end-effector frame, and

base

as the

end-effector orientation in the base frame, the gravity

vector in the sensor frame is given by:

med



base

med



base

(4)

Figure 15: Sensor frames and tool center of mass.

For each static pose i, the measurements satisfy

the linear system:







med

− m

med

− m

med







| {z }

b∈R







3×3

−m

med

]

3×3

−m

med

]







| {z }

A∈R

6N×9





med

bias

med

bias

med

CoM





| {z }

X∈R

(5)

Here, [g

med

]

is the skew-symmetric matrix asso-

ciated with the gravity vector at pose i, in the sen-

sor frame. Using measurements from N static poses,

this overdetermined system is solved thanks to least

squares to identify unknown parameters:

X = (A

−1

b (6)

3.3.2 Gravity Compensation

After estimating bias, handle mass, and centre of

mass, sensor outputs are compensated to isolate the

human-applied forces.

The sensor orientation relative to the base frame

base

med

, and the gravity vector in the sensor frame

is:

med



base

med



base

(7)

The gravitational force and moment on the sensor

are:

med

gravity

= m

med

gravity

med

CoM

× f

med

gravity

(8)

The compensated force and moment in the sensor

frame are then:

med

ext

= f

med

measured

− f

med

bias

− f

med

gravity

med

ext

= τ

med

measured

−τ

med

bias

−τ

med

gravity

(9)

The resulting vector F

med

ext



med

ext





med

ext



∈ R

represents the force and

torque applied by the human operator, expressed in

the sensor frame and compensated for sensor bias

and gravitational effects.

3.4 Compliant Control

Once the force applied by the human operator has

been estimated according to Equation 9, it is ﬁrst ex-

pressed in the operator frame h (see Equation 10),

which is attached to the handle and deﬁnes the hu-

man–tool interaction interface (see Figure 14).

int



med

3×3



med



med



med

ext

(10)

Here,

med

denotes the rotation matrix of the

interaction frame h to the sensor frame (med), and

med

is the position vector of the origin of frame h

expressed in the sensor frame.

Rather than using on position control, the control

strategy presented in this section is based on velocity

control, which is more appropriate for the dynamic

characteristics of the intended task. In the same way,

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

546

an admittance-based control law is used to compute

the Cartesian velocity in response to external forces

applied by the human operator.

The desired Cartesian velocity is obtained

by integrating the acceleration generated by a

mass–spring–damper model, as deﬁned in Equation 2.

This velocity determines how the robot should move

within the task space in order to respond compliantly

to the operator’s efforts. It is initially computed in the

operator frame h and then transformed into the robot

end-effector frame, as shown in Equation 11.







−

[

]

3×3



| {z }

∈R

6×6

(11)

Here,









denotes the com-

pliant motion resulting from the control law, ex-

pressed in the interaction (operator) frame h. The ro-

tation matrix

represents the orientation of frame

h with respect to the robot end-effector frame. The

vector

represents the position of the end-effector

origin expressed in frame h, and [

]

denotes its

skew-symmetric matrix. The full matrix multiplying

corresponds to the adjoint transformation Ad

which maps spatial velocity (twists) from the interac-

tion frame to the robot end-effector frame.

The resulting Cartesian velocity, now expressed

in the end-effector frame, is mapped to joint veloci-

ties

using the inverse of the robot Jacobian

−1

These joint velocity commands are subsequently sent

to the low-level joint velocity controller of the robot

for execution.

3.4.1 Example of a Compliant Motion

As an initial implementation, a simple compliant con-

trol scheme was developed based on the general form

of the admittance equation, given in Equation 12:

= M

−1



int

− D



(12)

In this formulation, M

and D

denote the de-

sired Cartesian inertia and damping matrices, respec-

tively. The variables

and

represent the resulting

Cartesian acceleration and velocity in the interaction

frame h.

In this case, the stiffness matrix K

is set to the

zero matrix 0

6×6

, which means that the stiffness effect

typically present in admittance control is removed.

Consequently, the robot motion corresponds to dis-

placement induced purely by the operator’s interac-

tion force, without any restoring force pulling the

robot back towards a desired or initial position x

The control parameters used in this implementa-

tion are as follows:







15.0 0 0 0 0 0

0 15.0 0 0 0 0

0 0 15.0 0 0 0

0 0 0 0.4 0 0

0 0 0 0 0.4 0

0 0 0 0 0 0.4













30.0 0 0 0 0 0

0 30.0 0 0 0 0

0 0 30.0 0 0 0

0 0 0 0.8 0 0

0 0 0 0 0.8 0

0 0 0 0 0 0.8







4 ROS2 ENVIRONMENT

The control environment was implemented in ROS2

and conﬁgured with a single force/torque sensor

(Medusa). The UR ROS2 driver package and all re-

lated nodes operated at 500 Hz, matching the robot’s

internal control loop. The dedicated node for the

Medusa sensor ran at 800 Hz, with measurements in-

terpolated in the compliant control node to align with

the robot control frequency.

The system architecture, shown in Figure 17, in-

cluded three main ROS2 nodes. The F/T Sensor

Medusa node published sensor data, ﬁltered inter-

nally by the sensor with a built-in cutoff frequency,

to the compliant control node, while also interfacing

with the EtherCAT reader Python script through an

internal TCP socket. The Compliant Control node

subscribed to the sensor data and published the end-

effector target velocity. Finally, the Cartesian Velocity

Controller node computed joint velocity commands,

which were transmitted to the UR ROS2 driver for

execution by the UR30 robot.

System-level optimisation included CPU isola-

tion and real-time scheduling in FIFO mode. Dy-

namic memory allocation was reduced and computa-

tional cost minimised, providing more deterministic

behaviour compared with standard implementations.

Sensor initialisation and setup were carried out

through dedicated safety routines, triggered manu-

ally from the terminal. In this conﬁguration, only the

built-in safety functions of the UR30 robot were en-

abled. Future extensions will integrate external safety

layers, including 3D vision. The Cartesian velocity

controller also accounted for the robot’s maximum

joint velocity and torque limits, saturating commands

when necessary to prevent unsafe execution.

Jitter, which quantiﬁes the variability of the con-

trol loop period, can be expressed as the difference

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process

547

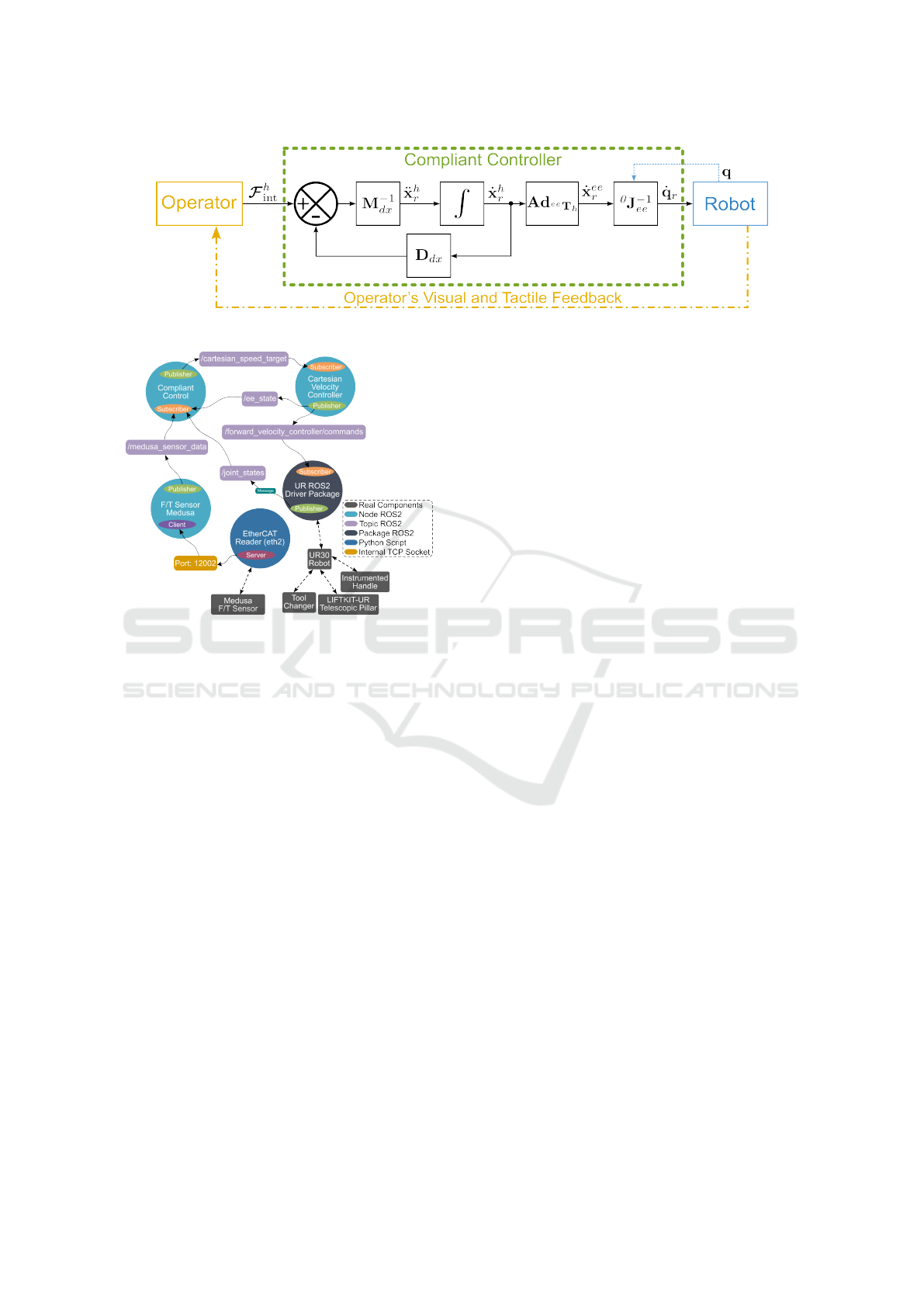
Figure 16: Block diagram of the implemented compliant control.

Figure 17: ROS2 control environment with one force/torque

sensor.

between the current loop period T

cur

and the nominal

period T

nom

Jitter = |T

cur

− T

nom

| (13)

Figures 18a and 18b show the measured loop jit-

ter for the compliant control node without and with

a real-time (RT) kernel, respectively. Using the stan-

dard kernel, signiﬁcant jitter peaks exceeding 500 µs

were observed, whereas the RT kernel maintained jit-

ter consistently below 250 µs. This demonstrates a

clear improvement in temporal determinism when us-

ing real-time scheduling.

Figures 19 shows the end-to-end latency of the

control loop. Without real-time kernel, the mean la-

tency was 1881.4 µs with peaks above 2 ms, indicat-

ing delays within the 500 Hz loop. With real-time

kernel, the mean latency decreased to 541.2 µs, with

no peaks beyond 2 ms.

5 EXPERIMENTAL RESULTS

The previous sections described the integration of a

dual force/torque sensing architecture into the instru-

mented tool. However, the preliminary experiments

reported here were conducted using only the Medusa

sensor mounted on the tool.

The test scenario consisted of standard cutting

movements representative of a meat processing task.

Speciﬁcally, slow forward motions were executed

along the cutting direction, followed by rapid re-

turn movements towards another part of the meat

piece. These simpliﬁed yet representative conditions

were chosen to evaluate the dynamic behaviour of

the admittance-based compliant controller under hu-

man interaction in a meat-cutting use case. In this

conﬁguration, only the displacement of the robot was

controlled in response to the operator’s applied force,

as ampliﬁcation features were implemented but not

tested due to the use of a single sensor.

Figure 21a shows the estimated external force ap-

plied by the human operator, reconstructed from the

Medusa sensor data after bias and gravity compensa-

tion. In response, the compliant controller generates

a Cartesian velocity command as illustrated in Figure

21b.

To evaluate how well the robot tracks this refer-

ence motion, Figure 23a compares the commanded

Cartesian velocity with the measured velocity, derived

from joint encoders using the forward velocity kine-

matics:

robot

The correlation between both signals conﬁrms the

robot’s internal controller accurately follows the ve-

locity commands.

Figure 23b presents the estimated force applied by

the robot at the end-effector. This is obtained from the

joint torques thanks to the relation:

robot

−T

Excluding contributions from the tool’s own dy-

namics and gravity. The plot highlights the robot’s

passive response to external forces applied by the hu-

man operator.

The transparency of the compliant control was

evaluated using the variable Y

diff

, deﬁned as the ab-

solute difference between the measured and desired

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

548

(a) Loop jitter without a real-time kernel. (b) Loop jitter with a real-time kernel.

Figure 18: Comparison of loop jitter for the compliant control node under standard and real-time kernels.

(a) End-to-end latency without a real-time kernel. (b) End-to-end latency with a real-time kernel.

Figure 19: End-to-end latency from sensor data acquisition to robot command execution.

Figure 20: Illustration of the human operator applying a

force on the handle, resulting in a tool motion.

admittance gains:

˙x

int

, Y

mes

˙x

mes

int

, Y

diff

= |Y

mes

−Y

| (14)

where ˙x

is the commanded end-effector velocity in

the human reference frame, ˙x

mes

is the measured end-

effector velocity in the same frame, and F

int

is the

force applied by the human operator.

This ﬁrst indicator of transparency for the com-

pliant motion demonstrates good performance dur-

ing standard movements: the robot successfully fol-

lows the human-induced motion, particularly during

phases of nearly constant velocity. However, when

rapid and large forces are applied (notably around

40s in the plots), the co-movements are insufﬁciently

smooth. The motion is strongly damped, which re-

sults in peaks in Y

diff

. This limitation is primarily due

to the damping matrix used in the current implemen-

tation, which reduces the operator’s intended dynam-

ics. A second contributing factor could be the robot

itself, as observed in Figure 23a, where a signiﬁcant

discrepancy exists between the desired end-effector

velocity from the compliant controller and the mea-

sured value.

Future transparency indicators will be investi-

gated, focusing in particular on the frequency re-

sponse of the admittance rather than a simple absolute

deviation.

A promising direction for improvement is the im-

plementation of a variable damping matrix, as pro-

posed in (Sharkawy and Koustoumpardis, 2022), to

better reﬂect the operator’s intended accelerations.

This is particularly relevant for anatomical tasks such

as meat cutting, where the human performs motions

with frequent changes in direction and acceleration

amplitude.

These results are consistent with the existing lit-

erature and reinforce the practicality of implement-

ing Cartesian admittance control by generating joint

velocity commands. This approach beneﬁts from

low-level integration, allowing the robot’s internal

controller to ensure stable and responsive behaviour

through the management of ﬁltering, actuation limits

and dynamic consistency.

However, several limitations must be taken into

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process

549

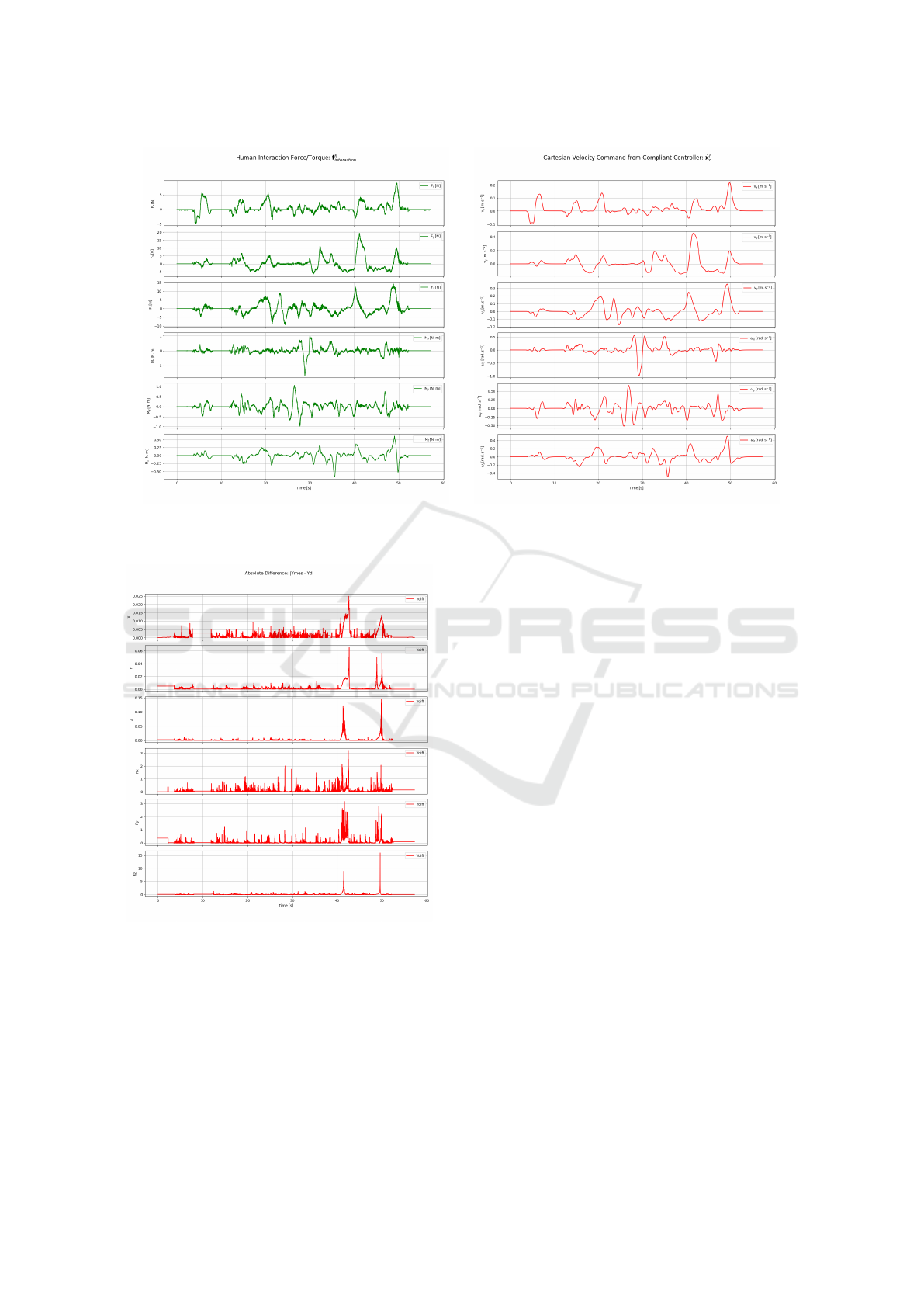
(a) Estimated human–robot interaction force. (b) Resulting Cartesian velocity.

Figure 21: Input and output of the compliant controller (expressed in the interaction frame h).

Figure 22: Absolute difference between measured and de-

sired admittance gains, Y

diff

, during compliant control.

account. Firstly, mapping Cartesian velocities to

joint velocities using the Jacobian can become ill-

conditioned near singularities, resulting in large joint

movements or noisy behaviour. Secondly, this strat-

egy depends on accurate dynamic modelling and sen-

sor calibration, as any error in force estimation di-

rectly affects motion quality. Additionally, when the

control loop does not operate in real time or lacks suf-

ﬁcient frequency, latency can reduce responsiveness

and compromise safety.

6 CONCLUSION

This paper has presented the design and preliminary

results of the control of an operator-assistance system

integrated into a collaborative robot for the manipu-

lation of soft bodies, such as in meat-cutting tasks.

The system combines a carefully instrumented end-

effector with a Cartesian admittance controller to en-

able compliant and intuitive physical human-robot in-

teraction.

The mechanical design of the instrumented tool,

featuring dual force/torque sensors, has been val-

idated to effectively distinguish between operator-

applied forces and interaction forces with the soft ob-

ject. The communication infrastructure and control

strategy, based on velocity commands and admittance

control, have demonstrated promising preliminary re-

sults in delivering responsive and stable assistance.

Future work will focus on in-depth experimen-

tal validation in realistic industrial scenarios, on im-

proving the robot’s force control capabilities using a

method distinct from that proposed in (Hamad et al.,

2021), and on integrating adaptive control schemes to

manage the variability in the direction of force and

acceleration typically applied by the operator in tasks

such as meat cutting. Moreover, the integration of

advanced perception modalities and operator intent

COBOTA 2025 - Special Session on Bridging the Gap in COllaborative roBOtics: from Theory to real Applications

550

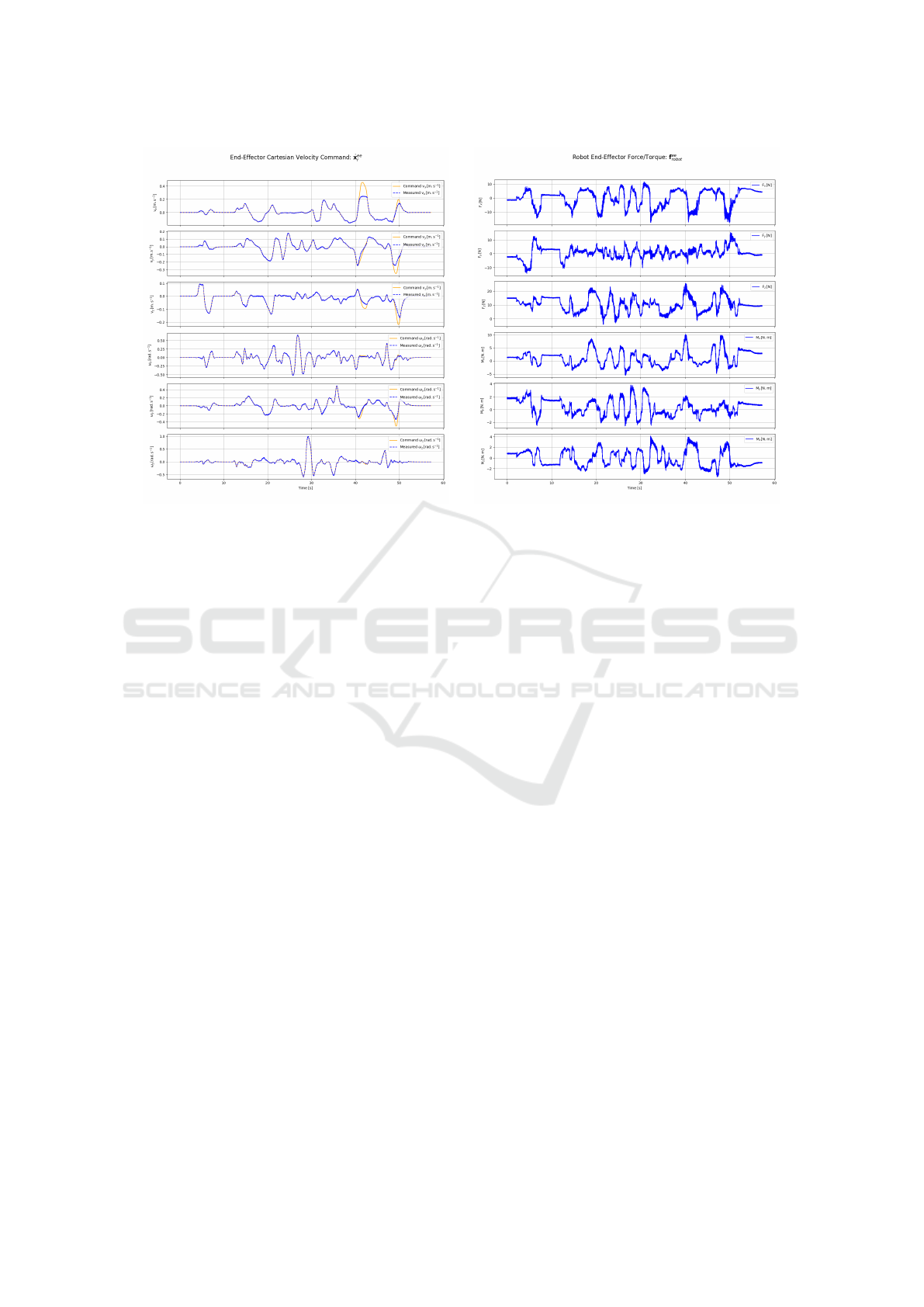
(a) Comparison between commanded and measured

end-effector velocity.

(b) Estimated force applied by the robot at the end-

effector.

Figure 23: Robot behaviour during compliant control.

recognition is expected to further enhance the sys-

tem’s robustness and usability.

Overall, this study lays the groundwork for the de-

velopment of collaborative robotic systems capable

of safely and efﬁciently manipulating deformable ob-

jects, while providing ergonomic assistance in tasks

involving soft body interaction. This opens new

opportunities for automation in complex, human-

centred industrial environments.

ACKNOWLEDGEMENTS

This work is funded by Interreg Sudoe, a European

Union funding program to support regional devel-

opment and cohesion in the regions of southwest-

ern Europe, as part of the ROBOTA Sudoe project

(S1/1.1/P0125): Robotics, Automation, and Digiti-

zation as Drivers of Competitiveness and Growth for

SMEs.

REFERENCES

Ajoudani, A., Zanchettin, A. M., Ivaldi, S., Albu-Sch

affer,

A., Kosuge, K., and Khatib, O. (2017). Progress

and prospects of the human–robot collaboration. Au-

tonomous Robots, 42(5):957–975.

Farajtabar, M. and Charbonneau, M. (2024). The path

towards contact-based physical human–robot interac-

tion. Robotics and Autonomous Systems, 182:104829.

Hamad, Y. M., Aydin, Y., and Basdogan, C. (2021). Adap-

tive human force scaling via admittance control for

physical human-robot interaction. IEEE Transactions

on Haptics, 14(4):750–761.

Hogan, N. (1984). Impedance control: An approach to ma-

nipulation. In 1984 American Control Conference.

IEEE.

Keemink, A. Q., van der Kooij, H., and Stienen, A. H.

(2018). Admittance control for physical human–robot

interaction. The International Journal of Robotics Re-

search, 37(11):1421–1444.

Sharkawy, A.-N. and Koustoumpardis, P. N. (2022). Hu-

man–robot interaction: A review and analysis on vari-

able admittance control, safety, and perspectives. Ma-

chines, 10(7):591.

Preliminary Design and Control of an Operator-Assistance System Integrated into a Cobot, for Anatomical Meat-Cutting Process

551