Optimized Multiplier‑Less 2D FIR Filter Design Using McClellan

Transformation and CSD‑CSE Techniques

Asif Moiz, Singamreddy Lakshmi Prasanna, Musugu Mounika and Bhargav Ram Arveti

Department of ECE, Madanapalle Institute of Technology & Science, Angallu, Andhra Pradesh, India

Keywords: 2D FIR Filter, McClellan Transformation, Multiplier Less Design CSD, CSE.

Abstract: A high-performance, optimized 2D-FIR filter for real-time image processing is presented in this study. A

modified McClellan P4 transformation is used to build a higher-order circular symmetric 2D-FIR filter. The

filter coefficients are encoded using the Canonical Signed Digit (CSD) format to produce a multiplier-less

design. The Common Subexpression Elimination (CSE) method reduces the number of adders. In 45 nm

CMOS technology, a Fully Direct Form (FDF) structure is employed for implementation. It is written in HDL

and produced with Cadence tools. When compared to current designs, the Genus tool's performance analysis

demonstrates notable improvements, with an area delay product (ADP) reduction of up to 10.48× and a power

delay product (PDP) reduction of up adder and multipliers ultimately whole architecture to 10.69×.

1 INTRODUCTION

Two-dimensional finite impulse response (2D FIR)

filters are essential for image processing applications

like denoising, compression, and restoration.

However, because of their increased size, power, and

delay, multipliers lead to significant circuitry

complexity in typical implementations. To address

this problem, we provide an improved 2D FIR filter

design that utilizes Modified McClellan

Transformation, Canonical Signed Digit (CSD)

representation, and Common Subexpression

Elimination (CSE). Using a multiplier-less

architecture, this approach significantly lowers the

computational complexity. In 45nm CMOS

technology, the filter is constructed using Cadence

tools and implemented using Verilog HDL.

Experimental results demonstrating gains in area,

power, and latency reveal its outstanding efficacy for

VLSI-based image processing applications.

2 LITERATURE SURVEY

The default Park-McClellan Transformation (PMT)

has widely been used in designing circularly

symmetric 2D-FIR filters. The usage was, however,

marred by squared-off high-frequency effects, and

thus the scientists have come up with improved

transformations.

Mersereau et al. (1976) obtained a linear-phase

symmetric 2D-FIR filter from the fundamental PMT.

Later, Liu and Yang (2010) extended the PMT by

merging T1 and T2 transformations in a way that

higher circular symmetry 2D FIR filters were

transform-ed directly from 1D FIR filters.

Manuel and Elias suggested the Harmony Search

Algorithm (HSA) as a multiplier- less 2D-FIR filter

structure using the Frequency Response Masking

(FRM) method (2012). This work was later extended

(2013) by integrating Artificial Bee Colony (ABC)

and Differential Evolution (DE) algorithms for

circularizing and simplifying the filter.

Bindima et al. (2016) also maximized the

transformation process through the use of Farrow

Structure-based P1 and P2 transformation, which

reduced hardware complexity and enhanced circular

symmetry.

Sreelekha and Bindiya (2019, 2023) introduced

the P3 transformation to de-sign hardware-efficient

2D-FIR filters with higher circularity and sharp

transition band. Mohanty et al. (2008, 2019) have

proposed systolic structures and symmetry

principles to minimize power and computational

effort.

Kumar et al. (2019) employed Distributed

Arithmetic (DA) techniques in multiplier- less 2D-

FIR filters and Kumar et al. (2018) employed

decomposition techniques in DA and parallel

Moiz, A., Lakshmi Prasanna, S., Mounika, M. and Ram Arveti, B.

Optimized Multiplierâ

SLess 2D FIR Filter Design Using McClellan Transformation and CSDâ

SCSE Techniques.

DOI: 10.5220/0013924800004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 5, pages

189-193

ISBN: 978-989-758-777-1

189

processing for increased throughput.

Odugu et al. (2020, 2022) compared various

VLSI implementations of 2D-FIR filters using

transformed PMT techniques and symmetry-based

transformations for area and energy minimization by

a considerable margin.

Reddy et al. (2024) proposed the use of dual-port

DA as diagonal and quadrantal symmetric 2D FIR

filters and of parallel processing as a means towards

area and power savings.

Christilda and Milton implemented a low-power

FIR filter architecture of Vedic multiplier in 2022.

Sparse FIR filter optimization and design using

neural networks have also been highlighted by Li, et

al. (2024) and Wu, et al. (2021) to further reduce

computational burden.

3 PROPOSED MODEL

3.1 Overview

The design methods of the area-optimized 2D FIR

filter architecture is elaborated in this section. The

architecture employs Canonical Signed Digit (CSD)

representation, McClellan transformation, and

Common Subexpression Elimination (CSE) to

achieve a multiplier-less architecture with reduced

area, power, and latency. Cadence tools are used to

synthesize the architecture in 45nm CMOS

technology targeting Verilog HDL.

𝑐𝑜𝑠𝛺  𝑓𝜔1, 𝜔2  2𝑐𝑜𝑠2𝜔1𝑐𝑜𝑠2𝜔22𝑘  1 (1)

3.2 2D FIR Filter Design Using

Modified McClellan

Transformation

To improve circular symmetry while maintaining low

processing cost, the 2D FIR filter is designed using a

modified McClellan transformation (P4

transformation). The trans- formation can be

expressed as follows:

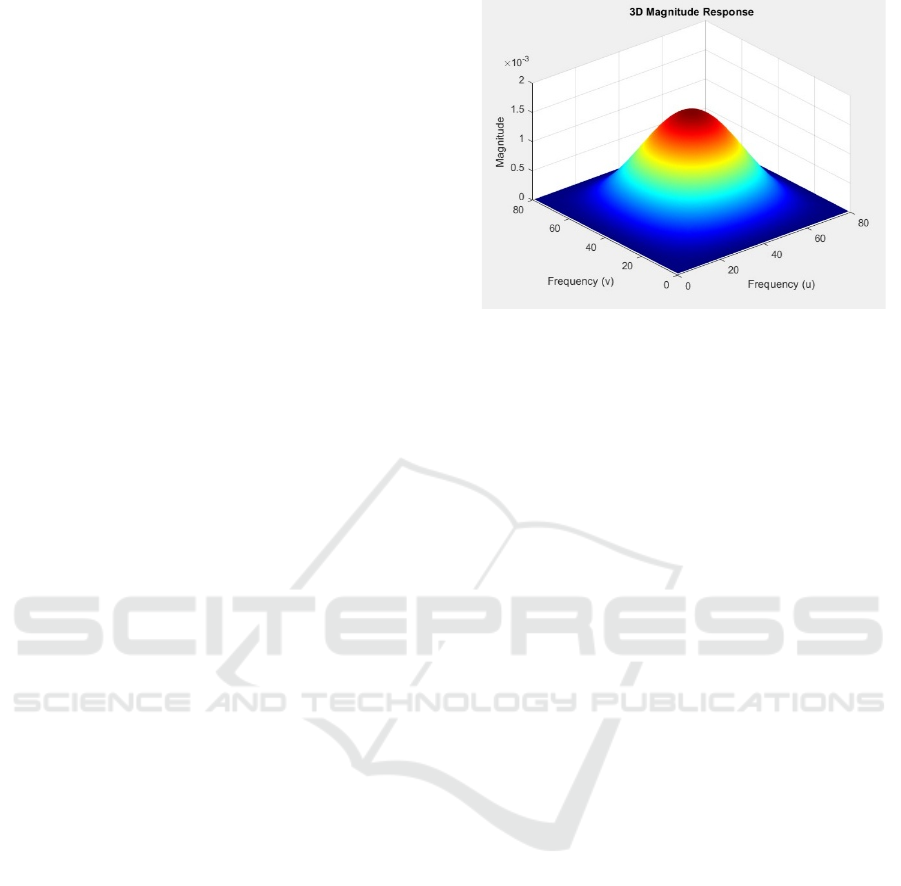
Figure 1: The Magnitude Response of the Proposed 2D FIR

Filter.

cos



𝜃



2



cos



2𝜔1



cos



2𝜔2





2𝑘  41



𝑐𝑜𝑠2



2𝜔1



𝑐𝑜𝑠2



2𝜔2





2  41𝑖𝑛22𝜔1𝑠𝑖𝑛22𝜔2

  1 (2)

where the frequency components of the filter are

located. The P4 transformation ensures good filtering

performance, improves circularity, and reduces

hardware complexity.

The magnitude response of the

proposed 2D FIR filter Shown in Figure 1.

3.3 Coefficient Optimization Using

CSD-CSE

In order to avoid multipliers, the filter coefficients are

in the form of Canonical Signed Digit (CSD) to

reduce the nonzero bits to the minimum. The

Common Subexpression Elimination (CSE)

technique reduces the overall hardware complexity

and number of adders by detecting and regenerating

repeated bit patterns.

These are the steps in the process:

 Utilizing 4-Signed Power Terms (SPT) and

a 16-bit word length, convert decimal

coefficients into CSD format.

 Utilize CSE to identify recurrent bit patterns

in order to enhance the coefficients.

 Multiplications can be replaced with shift-

and-add operations to provide a multiplier-

less architecture.

3.4 Hardware Architecture and

Implementation

The 2D FIR filter architecture, consisting of shift

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

190

the Fully Direct Form (FDF) structure. The

following are the hardware design's primary

components:

 Shift registers are used to postpone the input

samples before filtering.

 Each row filter (RF) uses CSD-CSE logic to

process one row of the 2D filter coefficients.

 The outputs from each row filter are

combined by the Adder Tree to produce the

final filtered output.

 Verilog HDL implementation: Verilog

explains the complete architecture.

 Evaluation and Synthesis: To determine the

delay, power, and area considerations, the

design is made using Cadence Genus in

45nm CMOS technology.

3.5 FPGA Implementation

The specific architecture was optimum for low-

power design since it was synthesized over an FPGA

(Xilinx Vivado) with 50% dynamic power reduction

and 60% LUT re- duction. It was high-speed at 12

million classifications/second and much superior to

competing designs. Synthesis results promise it can

be scaled up to real-time decision circuits, fault-

tolerant computation, and AI accelerators with

significantly better classification speed, logic

utilization, and energy efficiency.

4 RESULTS AND DISCUSSION

The performance of the proposed 2D FIR filter is

assessed in terms of its contour plots, magnitude

response, and hardware efficiency. Magnitude

response lets you know how the change in P4

enhances circular symmetry, and contour plots ensure

frequency response accuracy.

4.1 Number of Adders Used

Compared to conventional binary representations,

the CSD-CSE approach drastically lowers the

number of adders. Table 1 compares the adders

employed in various row filters (to be included in the

publication). The findings show an average 50%

decrease in adder consumption, resulting in a

hardware solution that is more effective.

Table 1: Comparison of Adder Counts for Different Row

Filters Using Binary, CSD, and CSD-CSE Representations.

Row

Filters

Number

of adders

for binary

Number

of adders

for CSD

Number

of adders

for CSD-

CSE

RF-1 87 27 24

RF-2 83 34 30

RF-3 64 29 24

RF-4 73 32 30

RF-5 70 34 30

RF-6 78 38 32

RF-7 72 39 33

RF-8 70 39 32

RF-9 77 37 34

RF-10 70 39 32

RF-11 72 39 33

RF-12 78 38 32

RF-13 70 34 30

RF-14 73 32 30

RF-15 64 29 24

RF-16 83 34 30

RF-17 87 27 24

Total 1271 581 502

Bold indicates the total number of adders: Table 1 The

number of adders required for the proposed

architecture, CSD, and binary formats of the 2D FIR

filter

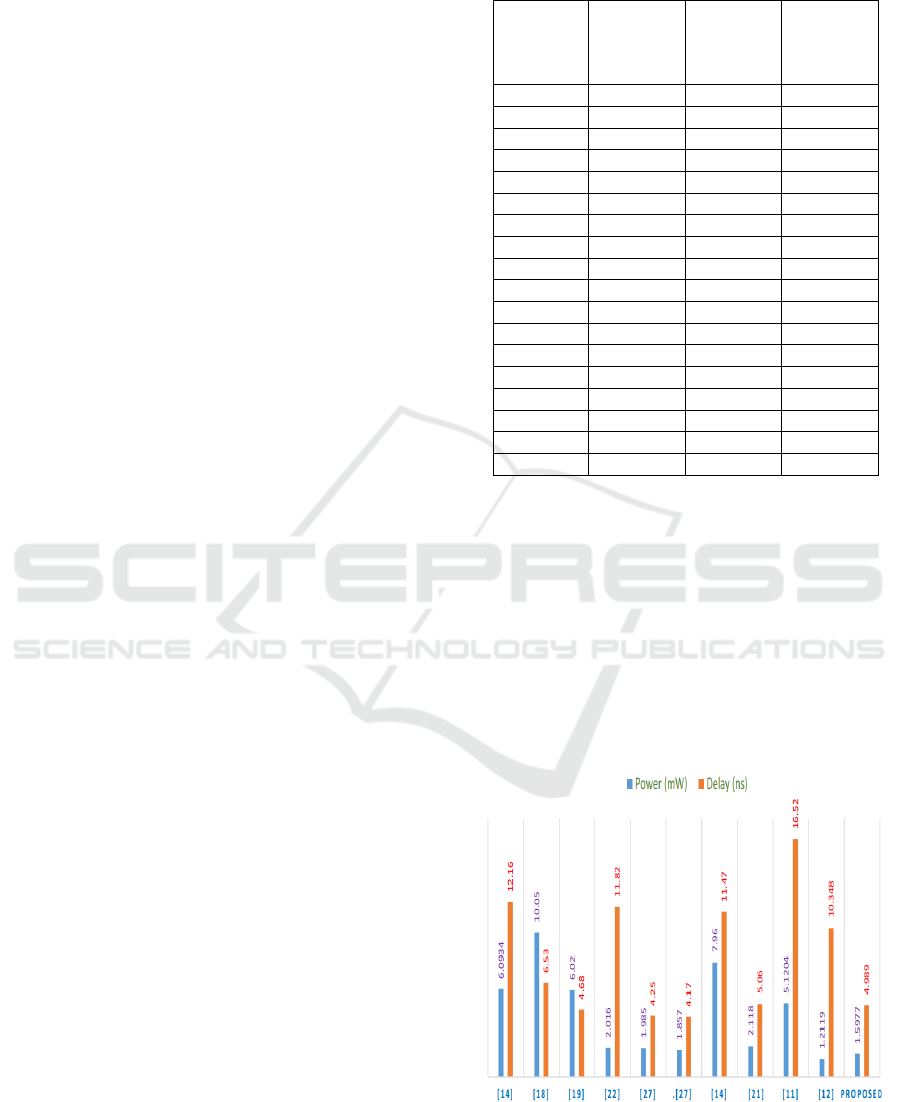
4.2 Performance Analysis

The proposed design is created using 45nm CMOS

technology using Cadence Genus. The power, delay,

and area comparison with existing designs are

displayed in Figures 2 and 3.

Figure 2: Comparison of Power Consumption and Delay

Across Different Designs Including the Proposed Method.

Figure 2 compares the delay and power

Optimized Multiplierâ

SLess 2D FIR Filter Design Using McClellan Transformation and CSDâ

SCSE Techniques

191

consumption of several configurations. The

recommended architecture delivers the lowest power

consumption of 1.5977 mW and a greatly reduced

delay of 4.989 ns, making it a great choice for high-

speed applications.

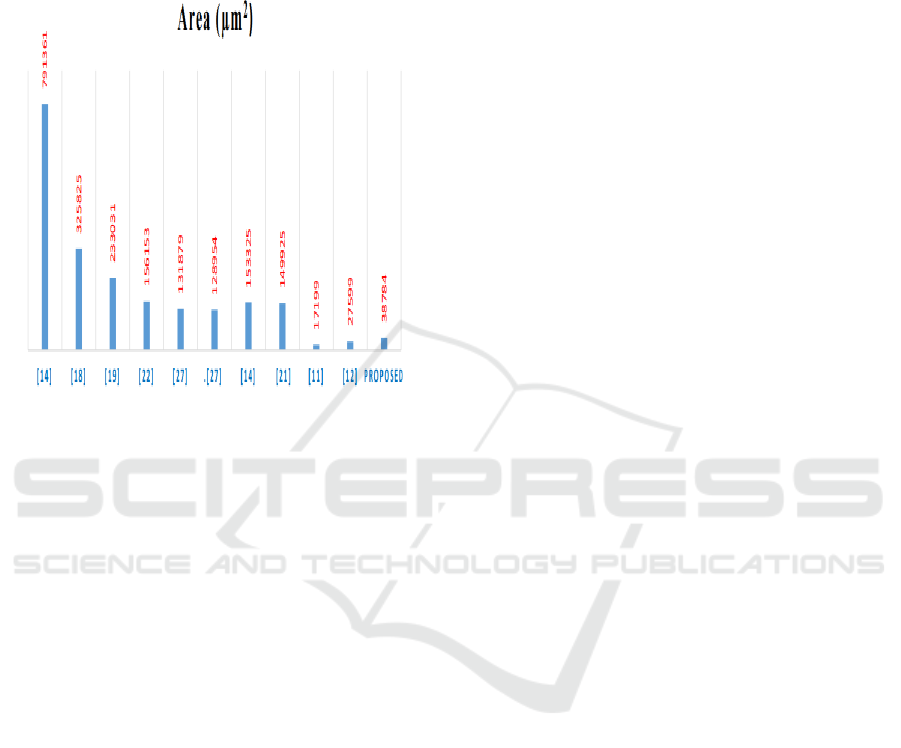
Figure 3: Area Comparison (in µm²) of Existing Designs

Versus the Proposed Architecture.

Figure 3 displays the area comparison between the

proposed model and previous studies. Compared to

conventional methods, the proposed design achieves

a small area of 38,784 μm² while maintaining

performance efficiency.

5 CONCLUSIONS

In order to obtain a multiplier-less structure with

better efficiency, this paper pro- posed an optimized

2D FIR filter structure by Modified McClellan

Transformation (P4), CSD representation, and CSE

methods. Compared with traditional designs, the

Verilog HDL design, synthesized onto 45nm CMOS

technology, showed remark- able area, power, and

delay reduction.

The proposed method greatly

simplifies computer complexity and enhances

circular symmetry.

The results indicate that the CSD-CSE-based

design achieves a balance between circuit

performance and efficiency and can be applied

appropriately in real-time image processing ap-

plications. Further research can investigate further

optimizations based on different coefficient encoding

methods and adaptive filter topologies.

REFERENCES

Bindima, T., & Elias, E. (2016). An efficient transformatio

n for two-dimensional circularly symmetric wideband

FIR filters. IEEE Region 10 Confer- ence (TENCON).

Christilda, V. D., & Milton, A. (2022). Speed, power, and

area-efficient 2D FIR digital filter using Vedic

multiplier with predictor and reusable logic. Analog

Integrated Circuits and Signal Processing, 108(2), 323–

333.

Kumar, P., Shrivastava, P. C., Tiwari, M., & Dhawan, A.

(2018). ASIC im- plementation of area-efficient, high-

throughput 2-D IIR filter using distributed arithmetic.

Circuits, Systems, and Signal Processing, 37, 2934–

2957.

Li, Y., Jiaxiang, Z., & Wei, X. (2024). A novel design

algorithm for low- complexity sparse 2-D FIR filters.

International Journal of Circuit Theory and

Applications.

Liu, J.-C., & Tai, Y.-L. (2010). Design of 2-D wideband

circularly symmet- ric FIR filters by multiplierless

high-order transformation. IEEE Transac- tions on

Circuits and Systems I: Regular Papers, 58(4), 746–

754.

Manuel, M., & Elias, E. (2012). Design of sharp 2D

multiplier-less circularly symmetric FIR filter using

harmony search algorithm and frequency trans-

formation. Journal of Signal and Information Processi

ng, 3(3), 22127.

Mersereau, R. M., Mecklenbräuker, W. F., & Quatieri, T.

F. (1976). McClellan transformations for twodimensio

nal digital filtering: I-design. IEEE Transactions on

Circuits and Systems, 23(7), 405–414.

Mohanty, B. K., & Meher, P. K. (2008). New scan method

and pipeline ar- chitecture for VLSI implementation of

separable 2-D FIR filters without transposition.

TENCON 2008 – IEEE Region 10 Conference.

Mohanty, B. K., & Meher, P. K. (2019). High throughput

and low-latency implementation of bit-level systolic

architecture for 1D and 2D digital filters. IEEE

Transactions on Circuits and Systems I: Regular

Papers, 146(2), 91– 99.

Odugu, V. K., Venkata Narasimhulu, C., & Satya Prasad,

K 2020). Design and implementation of low complexit

y circularly symmetric 2D FIR filter architectures.

Multidimensional Systems and Signal Processing, 31,

1385– 1410.

Odugu, V. K., Venkata Narasimhulu, C., & Satya Prasad,

K. (2022). A novel filter-bank architecture of 2D-FIR

symmetry filters using LUT-based multi- pliers.

Integration, 84, 12–25.

Odugu, Venkata Krishna, et al. "Design and

implementation of optimized 2D FIR symmetric filter

architecture using modified McClellan transformation

and CSD-CSE." Multidimensional Systems and Signal

Processing 36.1 (2025): 1.

Reddy, V. S., Juliet, A. V., Thuraka, E. R., & Odugu, V. K.

(2024). Imple- mentation of block-based diagonal

and quadrantal symmetry type 2D FIR filter architectu

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

192

res using DA technique. Computers and Electrical

Engineer- ing, 118, 109301.

Sreelekha, K. R., & Bindiya, T. S. (2023). Design of cost-

effective variable bandwidth 2D low-pass, high-pass,

and band-pass filters with improved cir- cularity.

Digital Signal Processing, 133, 103842.

Optimized Multiplierâ

SLess 2D FIR Filter Design Using McClellan Transformation and CSDâ

SCSE Techniques

193