A Comparative Analysis of Solving Sudoku Using Genetic Algorithm

and DLX

Manish S. R., Varshanth Reddy Y., Yuvraj R. and Gayathri Ramasamy

Department of Computer Science and Engineering, Amrita School of Computing, Amrita Vishwa Vidyapeetham, Bengaluru,

Karnataka, India

Keywords: Genetic Algorithm (GA), Dancing Links (DLX), Heuristic Exploration, Crossover, Mutation, Fitness

Evaluation.

Abstract: The Sudoku solving algorithms are very much essential for solving combinatorial optimization problems,

especially in areas of artificial intelligence, operations research, and recreational mathematics. This research

evaluates and compares the effectiveness of Genetic Algorithms (GA) and the Dancing Links (DLX)

algorithm in solving Sudoku puzzles, focusing on performance, computational efficiency, and accuracy. The

GA approach uses heuristics including population initialization, fitness evaluation, crossover, and mutation

for iterative approximation of solutions, whereas the DLX algorithm, also known as Algorithm X, translates

the Sudoku problem into an exact cover problem and employs a matrix-based linked list structure for

deterministic solution finding. The results of comparative analysis over a variety of puzzle complexities

indicate that the GA is considerably good at heuristic exploration. GA can solve relatively simpler puzzles

with ease but consumes much more computational resources for complex cases. Meanwhile, DLX always

obtains an exact solution with optimal efficiency but fails to explore suboptimal solutions flexibly. The results

show the strengths and weaknesses of both techniques, and offer substantial insight for algorithm selection

with criteria for problem conditions and complexity, relevant to a general class of larger combinatorial

optimization problems.

1 INTRODUCTION

Solving Sudoku has emerged as an important topic

within computational problem solving and

optimization, as Sudoku-solving is characterized by

its inherent complexity and practical relevance in

fields such as artificial intelligence, operations

research, and algorithmic research. The solving

algorithms for Sudoku not only evaluate the

efficiency of the algorithms but also cast insight into

the solution of other combinatorial optimization

problems. This work explores a comparative analysis

of two distinct approaches: Genetic Algorithms (GA)

and the Dancing Links (DLX) algorithm, each

representing a unique paradigm in the tussle to solve

Sudoku puzzles. The mechanism of GA is inspired by

the principles of natural selection and genetics. It uses

techniques such as population initialization, fitness

evaluation, crossover, and mutation iteratively to

refine solutions and navigate this vast solution space.

Therefore, its adaptability is high, but for problems

that are highly constrained, randomness can lead to

computational inefficiencies; that's why it is not

suited for moderately complex problems.

However, the DLX algorithm transforms the

Sudoku problem to be an exact cover problem and

solves it with perfect determinism. This is achieved

by using an efficient matrix-based linked list structure

that systematically ensures that all Sudoku constraints

are fulfilled with acceptable computational

efficiency. But the determinism limits the ability to

explore approximate or suboptimal solutions.

These methods are challenging in respect to

balance accuracy, computational efficiency, and

adaptability in solving Sudoku puzzles of various

complexities. While GA needs to deal with issues like

maintaining diversity in the solution pool and

avoiding premature convergence, DLX requires

careful handling of memory and computational

resources, especially when dealing with large or

dynamically changing problem instances.

This will be a project aiming to analyze and

compare the two methods in terms of performance,

efficiency, and accuracy for solving Sudoku puzzles.

R., M. S., Y., V. R., R., Y. and Ramasamy, G.

A Comparative Analysis of Solving Sudoku Using Genetic Algorithm and DLX.

DOI: 10.5220/0013918000004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 4, pages

631-637

ISBN: 978-989-758-777-1

631

Incorporating a number of benchmark puzzles at

different complexity levels, the analysis will weigh

the strengths and weaknesses of both approaches.

Additionally, a closer and more detailed analysis of

the trade-offs between heuristic exploration and

deterministic precision will be conducted to highlight

their applicability across different scenarios. These

findings will be all the better to enrich general

knowledge in combinatorial optimization algorithms

and their ability to solve similar complex problems.

There is a list of related works in Section 2. In

Section 3, the recommended methods are presented.

The findings are presented in Section 4. The

conclusion is presented in section 5. The future work

is presented in section 6.

2 RELATED WORKS

Pratama et al. dealt with heuristic-based methods of

solving Sudoku problem of varying degree of

difficulty. The abstract mentioned that the paper

addresses the efficiency and accuracy problems of

heuristic search algorithms. The authors used a

mixture of depth-first search and constraint

propagation methods to minimize the space of the

search. It relies on prioritizing cells with the fewest

possible candidates, which enhances speed and

accuracy. A major limitation is its vulnerability to

multisolution puzzles, which might deteriorate its

performance.

Lina et al. compared two algorithms in solving

Sudoku: Breadth-First Search (BFS) and Depth-

Limited Search (DLS). In the abstract, it briefly states

that each method will be understood for its

computational complexity and feasibility. BFS is

complete since it explores all possible possibilities

while having high memory usage. DLS, though has

reduced memory demands because it limits recursion

depth, may fail to find any solution. The core

limitation of this paper is that it simply cannot solve

the advanced Sudoku puzzles, due to scalability

issues with BFS and suboptimal depth limits with

DLS.

Jana et al. their paper presents a hybrid approach

combining Genetic Algorithm (GA) with the Firefly

Mating Algorithm (FMA) to solve Sudoku. The

abstract mentions that this synergy between GA's

exploration capability and FMA's local search

efficiency describes the capability of the hybrid

algorithm. The hybrid approach combines crossover,

mutation, and firefly-inspired movement to

iteratively improve solutions. Although the method is

generally good for many different scenarios, it has a

disadvantage of leading to higher overheads due to

the hybridization process, which makes it unsuitable

for real time.

Indriyono et al. presents a paper of traditional

backtracking and brute force methods of solving

Sudoku is conducted. The abstract is about the ease

and dependability of these methods for providing

accurate solutions. Backtracking uses a form of

recursive traversal, while brute force attempts to

exhaustively try all combinations. Although simple,

both approaches suffer from high time complexity

and are inefficient for more difficult puzzles.

Wang et al. their paper introduces an evolutionary

algorithm enhanced with local search strategies

targeting columns and sub-blocks in Sudoku puzzles.

The abstract on the algorithm indeed shows a balance

between exploration and exploitation.

Implementation details show integration of crossover,

mutation, as well as adaptive local search. Though it

is found effective, its limitation lies in the sensitivity

to poor initial populations, which leads to slow

convergence.

Bukhori et al. reviews an application of GAs

toward puzzle games, including Sudoku. The abstract

mostly emphasizes the versatility and adaptability of

the GA method. Standard genetic operations such as

selection, crossover, and mutation are observed to be

implemented with variations geared toward the

different types of puzzles being solved. This reviewer

found the review too generic, in which there was not

enough insight into domain-specific challenges or

optimizations uniquely particular to Sudoku.

Jana et al. presents Inspired by neighborhood

search, a new mutation mechanism to improve the

GA for Sudoku solving is discussed in this paper. The

abstract shows that there would be better convergence

rates due to targeted mutations based on cell

neighborhoods. The implementation adjusts the

mutation rates dynamically based on the quality of the

solutions obtained. However, this might not

generalize for all different puzzles due to its

parameter-dependent nature.

Bhasin et al. in their paper, the use of GAs to solve

the N-Puzzle problem, similar in complexity to that

of Sudoku. The abstract demonstrates the algorithm's

adaptability to combinatorial puzzles. Key genetic

operations with heuristic evaluations guide the search

process. A major limitation is its heavy dependency

on initial populations, whereby it degrades badly in

poorly initialized scenarios.

Silva et al. applies GAs to Beehive Hidato

puzzles, emphasizing adaptability to unique grid

configurations. The abstract highlights genetic

operations tailored to hexagonal grids. While the

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

632

implementation successfully generalizes GA to

different puzzles, its limitation lies in scalability, as

computational costs increase with puzzle size.

Sevaljevic et al. discusses the application of

Dancing Links implementations of the Exact Cover

Problem which directly applies to Sudoku. Abstract

Discusses DLX's efficiency in dealing with constraint

satisfaction problems. Implementation The DLX

Algorithm with use of dynamically variable

constraints based on linked lists. Its limitation relies

strictly on very precise formulations and offers little

margin of error in setup.

3 METHODOLOGY

3.1 Theoretical Structure

The focus of the Sudoku Solver project is on

designing an efficient system that would work to

solve Sudoku puzzles using two different

algorithms—Genetic Algorithm (GA) and Dancing

Links (DLX)—for a comparative study of their

efficiency. The solver aims to address the

computational challenge that occurs when solving

Sudoku puzzles of different levels of difficulty while

analyzing performance along key metrics of

execution time, accuracy, and adaptability.

The Genetic Algorithm (GA) applies an

evolutionary approach inspired by biological

operators such as crossover, mutation, and selection.

Starting from an initial population of random

potential solutions, the GA computes a measure of

how close each solution is to being a valid Sudoku

solution. Through generations, it applies operators of

selection, crossover, and mutation to evolve the

population toward finding a good solution. The

algorithm is particularly well-suited for puzzles

where heuristic or approximate solutions are enough

because it explores a diverse space and continuously

enhances solutions iteratively.

On the other hand, the Dancing Links (DLX)

algorithm takes advantage of the Knuth's Algorithm

X's ability to find the exact cover problem. DLX uses

a doubly linked list structure that facilitates an

effective representation of the Sudoku constraints and

adopts a backtracking mechanism for the

systematic exploration of all potential solutions. The

algorithm guarantees the fulfillment of each Sudoku

rule by every solution found and, therefore, is a very

effective algorithm to look for exhaustive solutions.

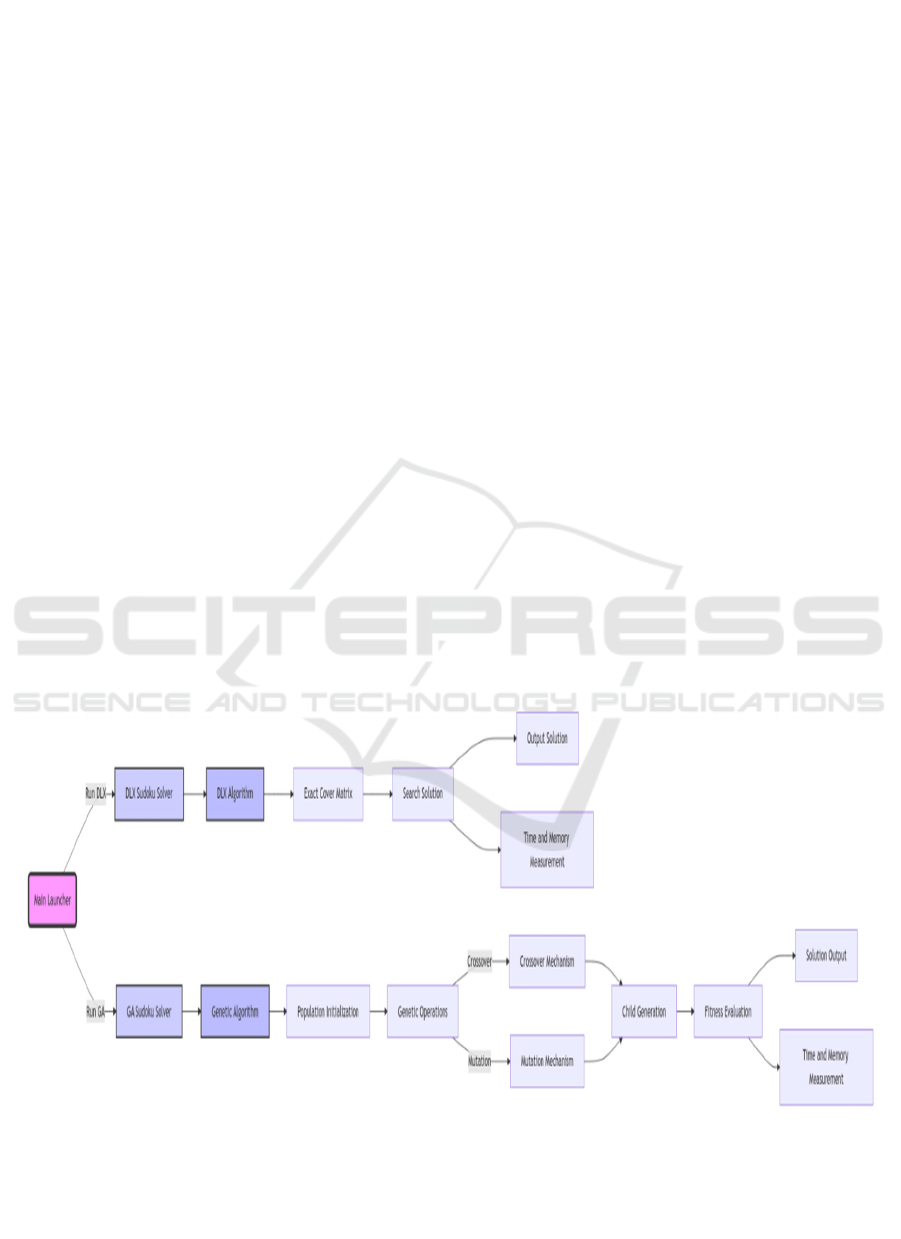
Figure 1: Genetic algorithm.

To assess the performance of these algorithms, a

comparative analysis is performed. The system

measures aspects such as:

1. Execution Time: The time taken by each algorithm

to solve the puzzles for various complexities.

2. Solution Accuracy: The solutions obtained are

valid and complete.

A Comparative Analysis of Solving Sudoku Using Genetic Algorithm and DLX

633

3. Resource Usage: Memory and computational

overhead for each approach

4. Adaptability: Performed ability across puzzles

with constraint density and sizes.

As an implementation aspect, this approach integrates

a test suite of Sudoku puzzles that validate the

algorithms. Under controlled conditions of

evaluation, the analysis highlights the strengths and

weaknesses of heuristic methods, such as GA, versus

deterministic approaches like DLX.

It not only documents detailed insight in two

contrasting algorithmic paradigms, but also

contributes towards the larger field of constraint

satisfaction problems. The results can have

implications on the establishment of hybrid or

adaptive solvers for the consideration of more similar

problem-solving strategies in actual applications. The

Genetic Algorithm is as shown in Figure 1.

3.2 System Overview

Input Interface: A user-friendly graphical

interface or command-line input for the users to

present the initial Sudoku puzzles. It should validate

that the input format follows the standard Sudoku

rules for the grid.

Algorithm Selection: Users can choose between

the two algorithms: GA or DLX. This module helps

ensure that the user is able to make a comparison over

the very same input for both algorithms.

Genetic Algorithm Module: This module

implements the GA, containing components for the

generation of a population, fitness evaluation,

crossover, mutation, and selection. It solves the

Sudoku puzzle heuristically and returns the solution

along with some performance metrics such as

execution time and fitness score.

Dancing Links Module: This module uses the

DLX algorithm that converts the Sudoku problem to

an exact cover one. Using a matrix-based approach, it

finds the solution deterministically and reports the

result along with the execution time.

Output Module: This component presents the

solutions generated by the selected algorithm, along

with performance metrics such as computational

time, accuracy, and number of iterations. It also

provides visualizations of the solved Sudoku grid for

better clarity.

Workflow: The workflow (illustrated in the

architecture diagram) begins by taking a Sudoku

puzzle as input. The user selects one of the two

algorithms to solve the puzzle. If GA is used, the

system generates an initial population, determines the

fitness and iterates through crossover and mutation to

find a solution. If DLX is used, the system converts

the puzzle into a binary matrix and applies the exact

cover technique to find the solution. The system will

then output the solution, its performance metrics and

a visual presentation of the solved grid.

Figure 2: Architecture diagram.

The workflow in Figure 2 reads a Sudoku puzzle and

normalizes it according to standard rules. Further, the

chosen algorithm might use the puzzle to generate

GA or DLX. The system computes performance

measurements such as execution time, accuracy, and

computational efficiency. The result is the solved grid

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

634

along with the comparative results of algorithms

used. This design thus offers a strong framework for

comparing the capability and performance of Genetic

Algorithms and Dancing Links in solving Sudoku

puzzles.

4 RESULTS AND EVALUATION

4.1 Statistical Evaluation

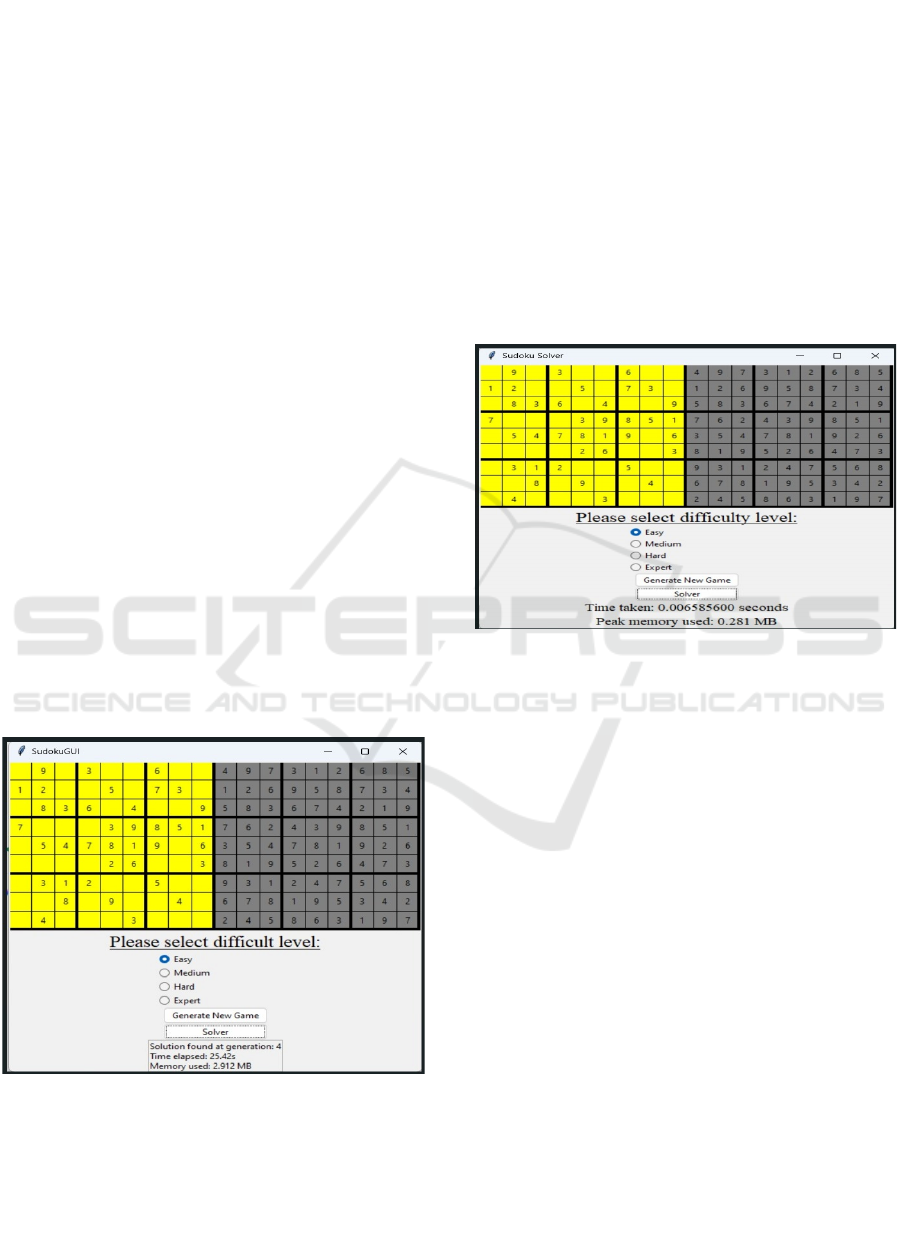
The number of difficulty variations is available as

well as options for new game generation as shown in

Figure 3. The fully filled grid thereby indicates that

the puzzle is completed effectively, as confirmed by

the indication of the solution after several iterations

of the interface. The overall performance metrics

presented here-in comprise time taken and memory

used, which are indicators of the resource

consumption involved in running the Genetic

Algorithm. The Genetic Algorithm has successfully

filled the Sudoku grid. It solves the puzzle correctly

with no conflicts or placement errors. It was also

reached within a computable number of generations,

signifying that the algorithm performs good

convergence towards the solution. The program

supplies information about the consumption of

computational resources: the time spent solving and

memory used, revealing the efforts made by a genetic

algorithm when using it to solve this particular type

of puzzle.

Figure 3: Genetic algorithm.

Options in the solver as shown in Figure 4 allow for

the choice of difficulty level and playing a new game

or solving an existing puzzle. The grid is fully filled

in, which results from the DLX algorithm's ability to

solve the puzzle effectively and with minimal time

with no errors. The puzzle is completely solved such

that the DLX algorithm accurately fills every cell

with a number based on Sudoku's strict rules. The

solver solves it so fast, which is an indication of

DLX's efficiency in running its algorithms to solve

constraint satisfaction problems quickly and

accurately. It only consumes a small amount of

memory, indicating the low overhead of the DLX

algorithm and its utility in applications where

resource computation is critical. This interface does

not only make it easy to solve Sudoku puzzles but

also shows the relevance of the DLX algorithm for

real-time applications and especially underscores

such an aspect as rapid processing with the use of

minimal resources.

Figure 4: DLX algorithm.

4.2 Comparison

The graph "Comparison of Execution Time by Puzzle

Size" as shown in figure 5c displays the performance

of the Genetic Algorithm (GA) and Dancing Links X

(DLX) across increasing Sudoku puzzle sizes (9x9,

16x16, 25x25). It illustrates how execution time

increases sharply in GA with puzzle size, indicating a

scalability problem, whereas the increase in DLX is

relatively less steep, indicating that DLX is much

more efficient and better scalable to larger puzzles.

Whereas GA might be competitive for small-size

puzzles due to potentially faster solutions, DLX's

continued performance over the whole range of sizes

makes it a choice for large-size challenges, where the

reliability and predictability of operation matter.

This comparison highlights DLX as an algorithm

of choice for hard tasks; indeed, GA needs additional

optimization or hybrid strategy in order to handle

sizeable puzzles properly.

A Comparative Analysis of Solving Sudoku Using Genetic Algorithm and DLX

635

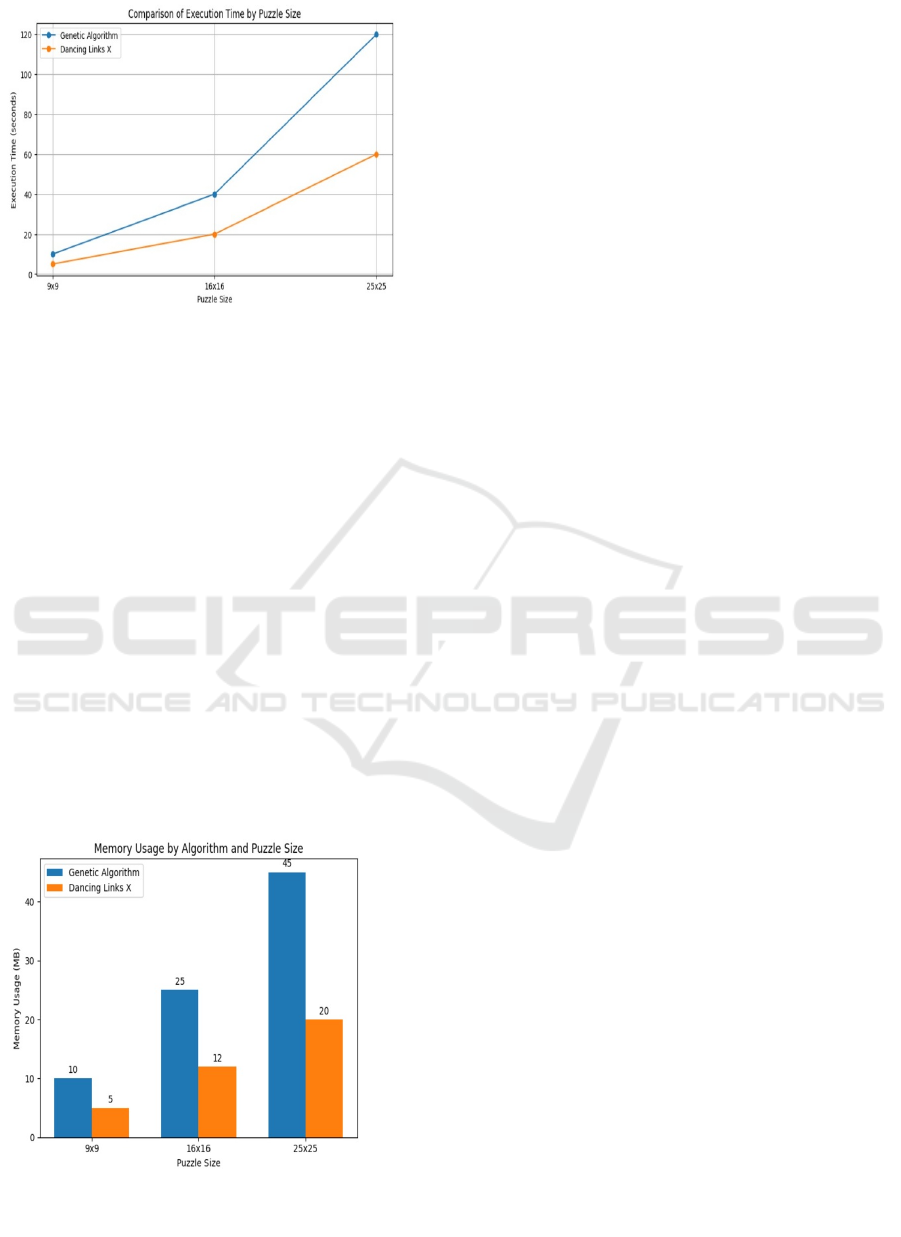
Figure 5: Comparison of execution time by puzzle size.

4.3 Memory Consumption

The bar graph as shown in figure 6d compares the

memory consumption of the Genetic Algorithm (GA)

and Dancing Links X (DLX) as they solve Sudoku

puzzles of varying sizes (9x9, 16x16, and 25x25). The

graph reveals that, with problem size, the memory

usage of GA really shoots up. For 9x9 problems, it

uses up to 10 MB and jumps to 45 MB for 25x25. This

therefore represents a very sharp increase as the

problem size increases. As compared to DLX, this is

much steeper; it uses 5 MB for 9x9 and 20 MB for

25x25 problems. This shows how DLX has good

memory performance, making it a better choice for

more complex problems where the memory

effectiveness is most valued. The comparison

between the two algorithms shows that GA requires

much more resources and how DLX is perfectly

suited for scenarios when free memory usage might

be very limited.

Figure 6: Memory consumption of GA and DLX.

5 CONCLUSIONS

Our work in this paper expands on these

developments concerning the methodologies for

solving Sudoku problems. We present a comparative

study of Genetic Algorithm (GA) and Dancing Links

(DLX) implementations. This is based on an analysis

of prior research, indicating that whereas exact

solutions are provided by techniques such as

backtracking and brute force, they do not overcome

the challenge of computations for bigger complex

puzzles. On the contrary, heuristic and hybrid

algorithms specifically those that use Genetic

Algorithms are scalable and efficient but are sensitive

to parameter tuning and incur some computational

overhead.

Dancing Links appears to be promising where the

problems can be constrained appropriately as

evidenced by its successful application to the Exact

Cover Problem. Its disadvantage would be that it

relies heavily on exact input formulations. The

juxtaposition of the two methodologies applied will

enable the strengths of evolutionary techniques for

adaptive applicability and the mathematical

correctness of DLX for precision.

Our work is a contribution to understanding the

performance of these different paradigms in finding

solutions for Sudoku puzzles with different levels of

difficulty. Through time complexity, convergence

behavior, and precision analysis, it is hoped that light

will be shed on their applicability. Therefore, our

effort eventually aims at developing a

computationally efficient yet adaptive robust

framework that propels state-of-the art combinatorial

problem-solving techniques forward.

6 FUTURE ENHANCEMENT

The horizon for future improvements upon this effort

includes hybrid approaches that integrate the fluidity

of Genetic Algorithms (GA) with the strength of

Dancing Links (DLX). These two methodologies

could effectively be integrated to create a solid

framework that capitalized on the best features of the

two methods, using the efficiency GA can produce

navigating difficult and vast search spaces and then

deploy DLX for solving exact constraints with

mathematical integrity.

In addition to this, machine learning techniques

would be used to dynamically optimize the

parameters of GA; this includes mutation rate,

crossover strategy, and selection mechanisms. The

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

636

second case is the use of machine learning models to

fine-tune configurations with DLX to achieve better

performance for a variety of Sudoku puzzles with

different degrees of difficulty.

The other areas for enhancement would be

extending this work into real-time applications.

Putting it into an interactive Sudoku solver or an

embedded system would then enable the algorithms

to be actually tested in the real world, measuring

responsiveness and accuracy under time constraints.

REFERENCES

Bukhori, Iksan, Jason Felix, and Saddam Ali. "Using

Genetic Algorithm to Solve Puzzle Games: A Review."

Journal of Computer Networks, Architecture and High-

Performance Computing 6, no. 1 (2024): 201-211.

Gurupriya, M., Ramasamy, G., Karthikeyan, B. (2023,

December). Combinatorial Bat Optimization for WSN

with Hoover Index Clustering. In 2023 International

Conference on Next Generation Electronics (NEleX)

(pp. 1-5). IEEE.

H. Bhasin and N. Singla, “Genetic based Algorithm for N -

Puzzle Problem,” Int J Computed Appl, vol. 51, no. 22,

pp. 44–50, Aug. 2012, doi: 10.5120/8347-1894.

Indriyono, Bonifacius Vicky, Ratna Wardani, Titin Susanti,

Laili Wulandari, Moh Fathurrohim, Rifka Sari Pratiwi,

and Endah Wulan Safitri. "Analysis of the Concept of

Solving the Sudoku Game Using Backtracking and

Brute Force Algorithms." International Journal of

Artificial Intelligence & Robotics (IJAIR) 6, no. 1

(2024): 40-47.

Jana, Sunanda, Anamika Dey, Arnab Kumar Maji, and

Rajat Kumar Pal. "A novel hybrid genetic algorithm-

based firefly mating algorithm for solving sudoku."

Innovations in Systems and Software Engineering 17,

no. 3 (2021): 261-275.

Jana, Sunanda, Anamika Dey, Arnab Kumar Maji, and

Rajat Kumar Pal. "A novel hybrid genetic algorithm-

based firefly mating algorithm for solving sudoku."

Innovations in Systems and Software Engineering 17,

no. 3 (2021): 261-275.

Krishna, K. S., Kumar, B. D., Reddy, M. D., Saketh, C. H.,

Ramasamy, G. (2024, May). A Multi-Class

Classification Framework with SMOTE Based Data

Augmentation Technique for Alzheimer’s Disease

Progression. In 2024 International Conference on

Advances in Modern Age Technologies for Health and

Engineering Science (AMATHE) (pp. 1-6). IEEE.

Lina, Tirsa Ninia, and Matheus Supriyanto Rumetna.

"Comparison analysis of breadth first search and depth

limited search algorithms in sudoku game." Bulletin of

Computer Science and Electrical Engineering 2, no. 2

(2021): 74-83.

M. M. P. Silva and C. S. Magalhães, “A Genetic Algorithm

for Solving Beehive Hidato Puzzles,” in Proceedings

XIII Brazilian Congress on Computational Intelligence,

ABRICOM, Jan. 2018, pp. 1–11. doi:

10.21528/CBIC2017-114.

Pratama, Moch Deny, Rifqi Abdillah, Darlis Herumurti,

and Shintami Chusnul Hidayati. "Algorithmic

Advancements in Heuristic Search for Enhanced

Sudoku Puzzle Solving Across Difficulty Levels."

Building of Informatics, Technology and Science

(BITS) 5, no. 4 (2024): 659-6671.

Ramasamy, G., Gurupriya, M., Vasavi, C. S., Karthikeyan,

B. (2024, May). A Cost-Sensitive Learning Approach

with Multi-Class Classification and Undersampling

Techniques for Pest Identification in the Coconut Leaf

Dataset. In 2024 3rd International Conference on

Artificial Intelligence for Internet of Things (AIIoT)

(pp. 1-5). IEEE.

S. K. Kumar, N. Dinesh and N. L, “Depression Detection

in Twitter Tweets Using Machine Learning

Classifiers,” 2022 Second International Conference on

Interdisciplinary Cyber Physical Systems (ICPS),

Chennai, India, 2022, pp. 81-86, doi:

10.1109/ICPS55917.2022.00023. keywords: Machine

learning algorithms; Social networking (online);

Blogs;Support vector machine classification; Mental

health;Depression;Decision trees;Support Vector

Machine; Decision Tree;CNN;Naive Bayes;Line

Kernel Convolutional Neural Network.

Sevaljevic, Andrija, and Paul Bodily. "Comparative

Empirical Analysis of Dancing Links Implementations

to Solve the Exact Cover Problem." In 2024

Intermountain Engineering, Technology and

Computing (IETC), pp. 255-258. IEEE, 2024.

Wang, Chuan, Bing Sun, Ke-Jing Du, Jian-Yu Li, Zhi-Hui

Zhan, Sang-Woon Jeon, Hua Wang, and Jun Zhang. "A

novel evolutionary algorithm with column and sub-

block local search for sudoku puzzles." IEEE

Transactions on Games 16, no. 1 (2023): 162-172.

A Comparative Analysis of Solving Sudoku Using Genetic Algorithm and DLX

637