Hybrid Approach to Optimize Delivery Route with K‑Dimensional

Tree and Dijkstra’s Shortest Path Algorithm

Purab Sen, Aaditya Yadav, Abhishek Pandey, Samip Aanand Shah,

Mehul Singh Bhakuni and Gayathri Ramasamy

Department of Computer Science & Engineering, Amrita School of Computing, Amrita Vishwa Vidyapeetham, Bengaluru,

Karnataka, India

Keywords: K‑D Tree, Dijkstra’s Algorithm, K‑Nearest Neighbor, Shortest Path, Route Optimization.

Abstract: To overcome the inefficiency of the traditional routing methods when it comes to route planning, this paper

introduces a hybrid technique of K-D trees and Dijkstra's algorithm that can be used to plan optimal delivery

routes. As the number of deliveries points and areas grow in large-scale delivery networks, it becomes more

challenging to find the shortest path. The approach in this method uses K-D trees for spatial partitioning to

reduce search space by identifying the closest delivery locations. TIME HEFT (Time Heuristic for TSP) (Wu

et al., 2019) is a traditional TSP solving method based on heuristics. After determining the nearest neighbor,

Dijkstra’s algorithm calculates the shortest path ensuring that it optimally navigates the graph with the least

computational overhead. Designed to accelerate computation and scale far better than traditional methods,

this integration allows for route optimization. The implemented system using Java Swing, contains a user

interface that allows a vehicular route to be displayed interactively by inputting the delivery locations and

also providing the best route possible to the user. To prove its efficacy, we present the experimental results

demonstrating that our proposed approach not only significantly reduces the computation time but also

achieves comparably good accuracy compared to the baselines, indicating its effectiveness for the logistics

and delivery operations that require dynamic and efficient routing of goods.

1 INTRODUCTION

Delivery route optimization is one of the most used

concepts in modern logistics companies. Consumer

demand for speed and cost-effective shipping is on

the rise, accompanied by the need for sophisticated

solutions to make logistics networks more efficient

across companies. Indeed, one of the main challenges

in this process is deciding which course to take to

make deliveries to different places, particularly in a

large, geographically-distributed network.

Conventional route optimization methods have

clear computational challenges, particularly in

addressing a large volume of delivery points. Many

existing approaches leverage exhaustive search

algorithms that, even if comprehensive, can be

computationally expensive to implement, making

them hard to apply in a real-time logistics context.

Mandates for lower emissions and increased

utilization must be balanced with competing goals for

efficiency, yet current methods leave a lot to be

desired, with nona-linear optimization techniques and

other processes requiring huge amounts of

computational capacity.

This study proposes an integrated methodology

leveraging K-D trees and Dijkstra’s algorithm that

significantly enhances the optimization of delivery

routes. Dijkstra’s algorithm is one of the most known

algorithms able to return the shortest path in a

weighted graph, making it the go to algorithm to be

used in any logistics problem. This work greatly

enhances the efficiency by integrating K-D trees to

achieve spatial indexing, as well as complex searches

and fast route calculations.

This manuscript aims to demonstrate proof of

concept that this integrated approach can improve

the efficiency of logistics. This study will evaluate

this approach's performance in real-world situations

by conducting extensive testing against conventional

optimization approaches. The end goal of the findings

is to develop a scalable and computationally efficient

approach that can allow logistics companies to

574

Sen, P., Yadav, A., Pandey, A., Shah, S. A., Bhakuni, M. S. and Ramasamy, G.

Hybrid Approach to Optimize Delivery Route with K-Dimensional Tree and Dijkstra’s Shortest Path Algorithm.

DOI: 10.5220/0013917100004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 4, pages

574-580

ISBN: 978-989-758-777-1

optimise their delivery routes in a manner that will

reduce their costs while improving operational

efficiency.

2 RELATED WORKS

Since then, over the past decades research has carried

on using K-Dimensional trees for spatial partitioning

and Dijkstra’s method for computing the shortest

path. In (Chowdary, K. Pranith, et al, 2023) a KNN-

KD tree algorithm was presented to improve

computational complexity and enhance the efficiency

of searching. Also, using a common location-based

application such as Google maps (Makariye, Neha,

2017) investigated K-Dimensional trees and KNN

searching methods to find out nearest cities. An

efficient KNN (k-nearest neighbor) query

mechanism was proposed handling a large number of

datasets, which was not depending on data

parallelism, and could index a new batch of data in

parallel in (Kumar, R et, al, 2017). In (Xiong, Jian, et

al, 2020) the KNN search times were additionally

optimized by embedding balanced binary trees into

K-D trees and using distance formulas that would

influence the accuracy of classification.

The conventional method to approach the

problem is with the use of Dijkstra. It was used for

pathfinding in congested areas in (Jo, Jaemin,2017)

and (Hou, Wenfeng, et al, 2018) enhanced it and

applied it to logistics transportation systems using

MapReduce to calculate the shortest paths with help

of Google Maps city distance data. The authors in

(Candra, Ade, et, al, 2020) discussed a modified

version of Dijkstra’s algorithm to solve passenger

train scheduling problem addressing the Split

Demand of One-to-One Pickup and Delivery

Problem.

Overall, the multitude of studies provide

definitive proof that KNN search algorithms and K-D

trees are practical in their utility in nearest neighbor

queries and that Dijkstra’s algorithm is worthwhile in

its optimization of shortest path queries. Similar

methodologies were performed on different domains,

such as recommendation systems, location-based

services, transportation networks and traffic

management which led to better accuracy and

improved computational efficiency.

3 BACKGROUND

3.1 K-Dimensional Tree (K-D Tree)

A K-Dimensional Tree which goes by its abbreviation

K-D Tree functions as a spatial partitioning data

structure for efficient geographical data organization

and proximity search applications within

computational geometry frameworks. The data

structure finds its primary use in multiple dimensional

search functions specifically nearest neighbor

detection and range scanning operations. A K-D Tree

possesses a binary structure which contains K-

dimensional points throughout its nodes and separates

data through multiple dimensions to produce two

partitioned regions during each tree level. The

partition structure of K-D Trees leads to improved

search efficiency which makes them beneficial in

geographic information systems and machine

learning applications and robotic systems.

3.2 K-Nearest Neighbor (KNN)

The K-Nearest Neighbor algorithm functions as a

direct non-parametric instance-based model that

applies both classification and regression purposes. A

specific input is assigned predictions through KNN

by leveraging K data points which are nearest to it and

applying either majority vote classification or

regression averaging methods. KNN requires a

distance metric among Euclidean, Manhattan or

Minkowski distance to calculate similarity. The

implementation process is straightforward yet the

calculation for large datasets becomes

computationally expensive.

3.3 Dijkstra’s Algorithm

Dijkstra’s algorithm is a foundational computer

science algorithm that is used to determine the

shortest route in a weighted graph. This optimization

scheme is applicable only in case of every edge

weight being positive to explore the best network

path. It serves as a key component behind much of

GPS routing, network processes, geographic

mapping, and city planning. As a result, it is an

indispensable tool utilized to solve both navigation

and connectivity problems in the real world.

4 METHODOLOGY

The work presented integrates K-D Trees with

Hybrid Approach to Optimize Delivery Route with K-Dimensional Tree and Dijkstra’s Shortest Path Algorithm

575

Dijkstra’s algorithm to optimize routes for delivery

networks. It targets a modification of specific

business processes to overcome computational

challenges associated with large and growing data

volumes. To prove the effectiveness of this new

model, the study looks at the geographical region of

Andhra Pradesh to illustrate its powers in the Indian

context. This methodology contains two main

components, which are a K-D Tree-based spatial

partitioning index structure and a shortest path search

using Dijkstra’s algorithm.

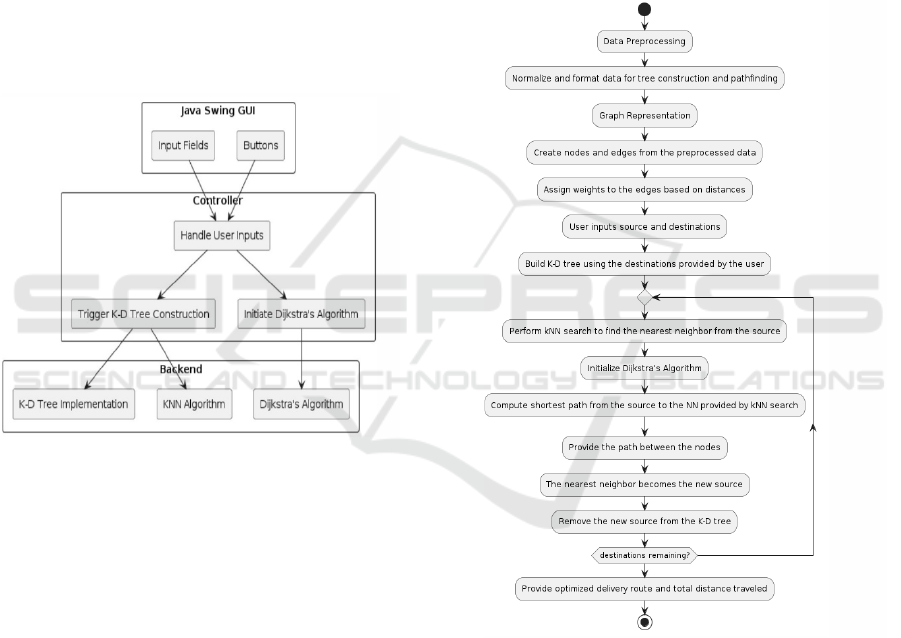
4.1 Architecture Diagram

The design of GUI uses Java Swing to create a user-

friendly interface with available user input fields.

The architectural diagram presents itself as the

Figure 1 below.

Figure 1: Architecture diagram.

4.2 Working of the Algorithm

4.2.1 Spatial Partitioning Using K-

Dimensional Tree

Step 1: Construction of the K-D tree.

The algorithm begins by prompting the user to input the

starting location along with the number of delivery

destinations and their respective names. Using this

information, a balanced K-D Tree is constructed,

organizing the delivery points efficiently in a multi-

dimensional space.

Step 2: Querying Nearest Neighbors

To optimize route selection, the k-Nearest Neighbors

(kNN) search is performed using K-D Tree. This step helps

in identifying the nearest delivery points relative to the

starting location. The Haversine formula is applied to

compute distances, ensuring accuracy in determining

proximity. This approach minimizes computational

complexity by narrowing the search area to nearby

locations.

Distance Calculation by Haversine Formula:

cos

-1

(sin(l1). sin(l2)+cos(l1)+cos(l2).cos(long2-long1)).R

where,

l1 = latitude of the first location

long1 = longitude of the first location

l2 = latitude of the second location

long2 = longitude of the second location

R = 6371 Km, radius of Earth

4.3 Workflow

The algorithm’s workflow diagram is demonstrated in

Figure 2.

Figure 2: Workflow diagram.

4.3.1 Calculation of shortest path using

Dijkstra algorithm

Step 3: Representation of Graph.

Each node within the graph contains a list that shows

neighboring nodes together with their corresponding

edge weights. This arrangement forms the basis for

creating the graph.

a. Nodes: Each node represents a junction derived

from the geographical data of Andhra Pradesh. It is

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

576

uniquely identified and contains coordinate details,

including latitude and longitude.

b. Edges: The weighted edges within the model

connect junctions through their paths and roads. Each

weight represents the distance between nodes, and it

exists between the starting and ending nodes as

designated by weighted edges. The program retrieves

distance data from Google Maps to complete the map.

Step 4: Applying Dijkstra’s’ Algorithm

Dijkstra’s’ algorithm is employed after node and edge

definition for identifying the shortest path from an

initial node to its nearest KNN-based neighbor

through the K-D tree. The algorithm performs these

steps to determine the shortest route between the

beginning node and its most proximate node

(destination).

a. A table made from a 2-D array contains m

rows connected to three columns to represent all

nodes in the graph.

b. Nodes are represented by the first column

which is initialized with the IDs of the nodes. The

distance is represented by the second column which

is set to infinity (∞) for all nodes except the starting

node, which is set to 0.

c. The procedure starts by selecting the node

with the minimum value from its second column that

becomes the current node.

d. The weights of the edges for each

neighboring node are added to the current node’s

minimum distance and compared with the existing

values in the second column. If the new sum is

smaller, the table is updated with this value in the 2nd

column and the current node in the 3rd column.

e. The current node receives a visited label

and the following node selection considers the

unvisited node showing the minimum value in the

second column. The process moves forward to step g

when either no possible node exists, or the newly

updated current node represents the destination point

or the algorithm restarts at step d.

f. The stack functions to return the shortest

path sequence. First push the destination node to the

stack followed by storing its predecessor in the third

column. The process runs until the beginning node

becomes accessible.

g. Starting from the top of the stack the nodes

get removed sequentially to establish the shortest path

between beginning and target nodes.

4.3.2 Integration of KNN and Dijkstra’s

algorithm

A K-Nearest Neighbours (kNN) search is performed

using a KD-tree to find the delivery point closest to

the starting point. Using this method creates a spatial

indexing structure that organizes geographical data,

to allow for fast retrieval of the neighbour within.

The closest neighbour is then determined, and using

Dijkstra's algorithm, a mathematical path is

calculated between the departure point to the now

closest neighbour, again, to ensure minimal distance

travelled. When the nearest node is reached, it is

removed from the KD-tree and the closest node

search is repeated (the new node is the starting

point).

This iteration process repeats the KD-tree finds

the next nearest neighbour, Dijkstra’s algorithm

calculates the shortest distance between the route

already covered and those remaining to cover, and the

nearest node gets popped until all of the delivery

points have been visited. The total distance travelled

is updated each log cycle throughout the process.

When it has visited all the locations, the algorithm

terminates, and the final optimized route along with

the complete travel distance is presented on the

graphical user interface (GUI), giving a concise

overview of the efficiency of the delivery network

4.3.3 Observation

Figure 3 illustrates the output of the proposed

algorithm. The sequence in which locations are visited

is denoted by numerical labels in red, while the

corresponding path is represented using black lines

connecting the edges as shown in figure 3.

Figure 3: Final output.

Hybrid Approach to Optimize Delivery Route with K-Dimensional Tree and Dijkstra’s Shortest Path Algorithm

577

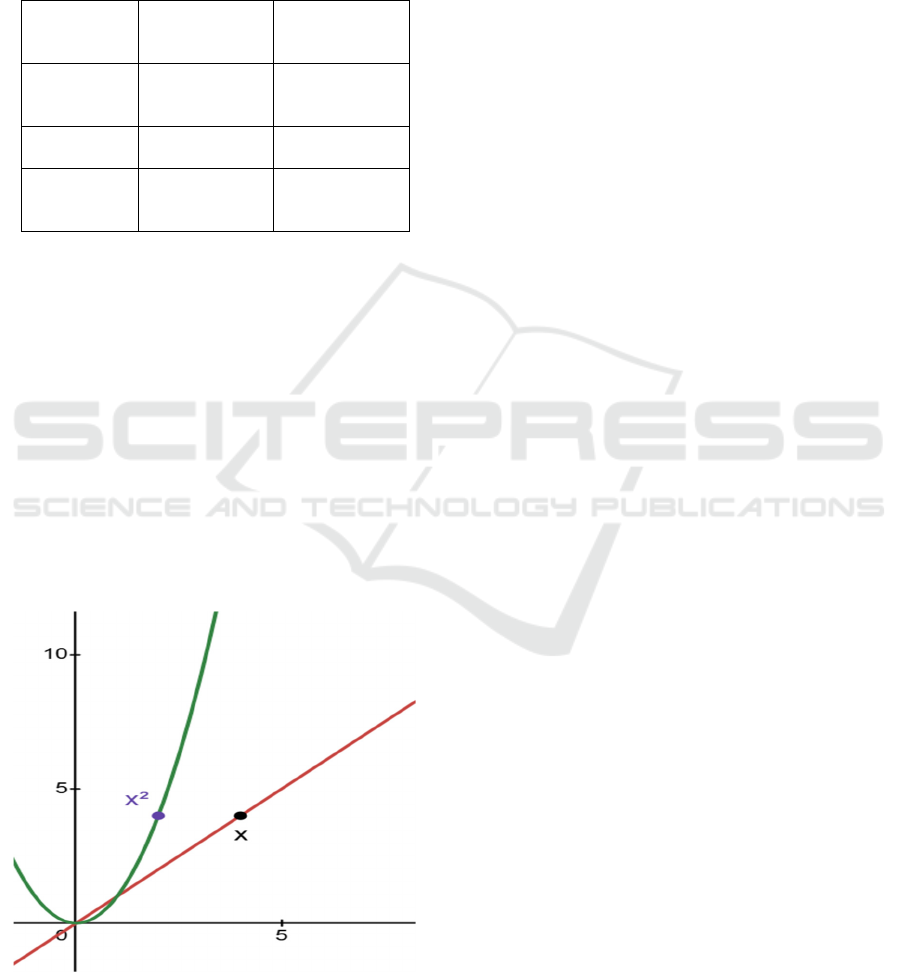
Table 1 presents a comparison between the

expected nearest neighboring locations and the actual

locations visited, based on the results illustrated in

Figure 3. The data in Table 1 demonstrates that the

algorithm proposed operates effectively, as expected

and visiting locations align consistently.

Table 1: Expected vs actual output.

S.No.

Expected

Locations

Actual

Locations

Visite

Kastubha

Gandhi Girl’s

Hostel

(

)

Kastubha

Gandhi Girl’s

Hostel

(

)

Duddukanta

(

)

Duddukanta

(

)

Jagan Reddy

Balapanuru AP

(

)

Jagan Reddy

Balapanuru AP

(

)

5 TIME COMPLEXITY

For Nearest Neighbors problem we have two core

approaches which are K-Nearest Neighbors (KNN)

method and Dijkstra’s algorithm. Both of them find

the nearest points in data sets but their time

complexities measure different computational

efficiencies. KNN algorithm is very efficient having

the time complexity of O (kn log n + k log k), which

means the number of operations needed to be

performed are reasonably high with respect to the

number of delivery locations (k) and dataset nodes

(n).

Figure 4: Analysis of time complexity.

In Roughly, this means Dijkstra's algorithm and

KNN have time complexities of O (k² n log n) Y O

(n²), and we can see that for small k KNN is way

faster than Dijkstra's algorithm, while for a huge

value of k, the computation KNN will still take much

more time than Dijkstra's algorithm. This differential

becomes sharper with a larger ‘k’ and suggests an

underrepresented advantage of KNN vs. other well-

studied routing problems.

Overall, figure 4 gives a graphical aspect of time

complexity growth for the two approaches.

6 RESULTS AND ANALYSIS

An assessment of the chosen routes validated the

efficiency of the proposed41[44] route optimization

system. Significant reduction in total travel distance

was recorded when compared with conventional

benchmark methods, thereby realizing time and cost

benefits for logistics carriers as well as shippers. The

use of K-D trees allowed for efficient realization of

optimal paths while Dijkstra’s algorithm was utilized

to ensure shortest route viable to rep multiple

destinations. This reduced diversions while

improving supply planning, leading to more efficient

deliveries.

Comparative analysis emphasized the system’s

role in lowering computational complexity and

processing time especially for cases where the

number of delivery points increased. Large datasets

were still the domain of computer/memory

management nightmares, but K-D trees and

Dijkstra’s algorithm allowed for efficient (relatively

speaking, of course) spatial data organization and

super speedy single-source shortest path discovery.

This design kept the functions separate and thus

reduced system overload, allowing for larger datasets

and elaborate routing plans.

That being said, heuristic-based optimizations

could potentially result in negligible augmentations

of travel distance as a byproduct of their

characteristics. Even so, the main benefit is the

substantial decrease in employment costs. Real-time

updates are crucial in large-scale logistics operations,

where delays can create congestion and cost money.

It is proposed as an energy-efficient system

addressing routing and computational issues and is

therefore a relevant solution for accelerating the

delivery network of businesses and enabling them to

remain competitive on the market.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

578

7 CONCLUSION AND FUTURE

IMPROVEMENTS

Overall, it was evident that K-D trees and Dijkstra’s

algorithm worked well together to improve delivery

route optimization, as you can see this kind of power

from combining data structures and algorithms in this

way. Traditionally applied for organizing multi-

dimensional spatial data for fast nearest-neighbour

searches, K-D trees helped pinpoint the best possible

delivery points. Leveraging Dijkstra’s algorithm for

shortest path determination based on weighted

graph1, the system devised an efficient, cost-

effective routing solution. This integration

immensely simplified the computational intensity

involved, making it possible for the system to adapt

in real-time and make quick decisions regarding

logistics.

In summary, the work presented here lays the

groundwork for further research and innovation in

delivery route optimization. In the case of the

potential application of Unmanned Aerial Systems

(UAS) for parallel drone deliveries, because all

queries do not require tree construction, K-D trees

enables the rapid computation of multi-point

delivery routes. It also improves safety and

operational efficiency of drone-based logistics and

provides flexibility which allows for real-time

adaptation to varying conditions and new delivery

requests, optimizing the overall system performance.

Although it is as accurate as they come, the

system’s wide-reaching nature offers up

opportunities for further improvement. Dynamic

processing of new requests while service delivery

operations are in progress could make route planning

a seamless process without disruption to serve new

operations at all times. New requests to the model

would regenerate K-D trees, using efficient

architecture and eliminating unnecessary data,

enabling real-time route optimization and optimizing

responsiveness to customers demands for better

service quality. This will empower logistics strategies

from cold chain toward delivery ops, and there is a

demand for further research and implementing the

system in daily practice.

REFERENCES

Andini, Diska, et al. "Adaptation of k-nearest neighbor

queries for inter-building environment." Computational

Science and Its Applications–ICCSA 2018: 18th

International Conference, Melbourne, VIC, Australia,

July 2-5, 2018, Proceedings, Part I 18. Springer

International Publishing, 2018.

Candra, Ade, Mohammad Andri Budiman, and Kevin

Hartanto. "Dijkstra’s and a-star in finding the shortest

path: a tutorial." 2020 International Conference on Data

Science, Artificial Intelligence, and Business Analytics

(DATABIA). IEEE, 2020.

Chowdary, K. Pranith, et al. "Exploring KD Trees and KNN

Search in the context of Google Maps: An Insightful

Overview." 2023 14th International Conference on

Computing Communication and Networking

Technologies (ICCCNT). IEEE, 2023.

Chung, Moonyoung, Soon J. Hyun, and Woong-Kee Loh.

"Efficient exact k-flexible aggregate nearest neighbor

search in road networks using the M-tree." The Journal

of Supercomputing 78.14 (2022)

D. S. Nair and P. Supriya, "Comparison of Temporal

Difference Learning Algorithm and Dijkstra’s

Algorithm for Robotic Path Planning," 2018 Second

International Conference on Intelligent Computing and

Control Systems (ICICCS), Madurai, India, 2018, pp.

1619-1624, doi: 10.1109/ICCONS.2018.8663020.

Deepa, G., et al. "Dijkstra Algorithm Application: Shortest

Distance between Buildings." International Journal of

Engineering and Technology 7.4.10 (2018): 974-976.

Gayathri, N., and KRM Vijaya Chandrakala. "A novel

technique for optimal vehicle routing." 2014

International Conference on Electronics and

Communication Systems (ICECS). IEEE, 2014

Hou, Wenfeng, et al. "An advanced k nearest neighbor

classification algorithm based on KD-tree." 2018 IEEE

International Conference of Safety Produce

Informatization (IICSPI). IEEE, 2018.

Jayasree, K. R., P. R. Jayasree, and A. Vivek. "Dynamic

target tracking using a four wheeled mobile robot with

optimal path planning technique." 2017 International

Conference on Circuit, Power and Computing

Technologies (ICCPCT). IEEE, 2017.

Jiang, Wei, et al. "Graph-Indexed k NN Query

Optimization on Road Network." Electronics 12.21

(2023): 4536.

Jo, Jaemin, Jinwook Seo, and Jean-Daniel Fekete. "A

progressive kd tree for approximate k-nearest

neighbors." 2017 IEEE Workshop on Data Systems for

Interactive Analysis (DSIA). IEEE, 2017.

Kaniz, Sharifa Tahmida, Jibon Naher, and Tanzima

Hashem. "Authentication of k nearest neighbor queries

in the presence of obstacles." 2017 4th International

Conference on Networking, Systems and Security

(NSysS). IEEE, 2017.

Kumar, R. Sathish, C. Rani, and P. Ganesh Kumar.

"Predicting shortest path for goods delivery to fair price

shops in India." 2017 4th International Conference on

Advanced Computing and Communication Systems

(ICACCS). IEEE, 2017.

Makariye, Neha. "Towards shortest path computation using

Dijkstra algorithm." 2017 International Conference on

IoT and Application (ICIOT). IEEE, 2017.

Sari, Indah Purnama, et al. "Implementation of Dijkstra’s

Algorithm to Determine the Shortest Route in a City."

Hybrid Approach to Optimize Delivery Route with K-Dimensional Tree and Dijkstra’s Shortest Path Algorithm

579

Journal of Computer Science, Information Technology

andTelecommunicationEngineering2.1(2021):134138.

Srinivasan, Madhura, and K. Sireesha. "Optimal Path

Finding Algorithm for Logistic Routing Problem."

2022 International Conference on Intelligent

Innovations in Engineering and Technology (ICIIET).

IEEE, 2022.

Tiwari, Vijay R. "Developments in KD Tree and KNN

Searches." International Journal of Computer

Applications 975: 8887.

Xiong, Jian, et al. "Split demand one-to-one pickup and

delivery problems with the shortest-path transport

along real-life paths." IEEE Access 8 (2020): 150539-

150554.

Zhu, Dan-Dan, and Jun-Qing Sun. "A new algorithm based

on Dijkstra for vehicle path planning considering

intersection attribute." IEEE Access 9 (2021): 19761-

19775.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

580