Comparative Analysis of Stock Price Prediction Models

Ch Amarendra, K. Parimala, R. Shivateja, B. Finney Vivek and K. Jashuva

Department of Advanced Computer Science and Engineering, Vignan's Foundation for Science, Technology & Research

(Deemed to be University), Vadlamudi, Guntur (Dt), Andhra Pradesh, India

Keywords: Long Short‑Term Memory (LSTM), Linear Regression, Moving Average, Mean Squared Error (MSE), R

Squared Error.

Abstract: Stock price prediction is the process of forecasting the future movements and trends in stock prices. It plays

a vital role in financial markets as it helps investors, traders, and financial institutions make informed

decisions regarding buying, selling, or holding stocks. It involves analysing historical price data, market

trends, economic indicators, and other relevant factors to develop predictive models. However, due to the

inherent complexities and uncertainties of financial markets, correctly forecasting stock values is a difficult

task. To improve prediction accuracy many machine learning techniques have been proposed. In this study,

the effectiveness of three alternative stock price prediction techniques like Linear Regression, Moving

Average, and Long Short-Term Memory are compared using the JPMorgan stock price prediction dataset.

The study’s findings demonstrate that the LSTM method forecasts stock prices more accurately than moving

average and linear regression by obtaining the lowest MSE of better prediction precision and a greater R

squared value of a small model-data fit. Performance of these approaches is assessed using the R-squared

error and Mean Squared Error (MSE).

1 INTRODUCTION

Stock price prediction is a critical area of research in

financial markets, aiming to forecast future

movements and trends in stock prices. Accurate

prediction of stock prices has significant implications

for investors, traders, and financial institutions,

enabling them to make informed decisions and devise

effective investment strategies. The complex and

dynamic nature of stock price data is often difficult to

capture using traditional methods for stock price

prediction, such as statistical models and technical

indicators. The primary goal of this study is to

compare the performance of different prediction

methods, including LSTM, Moving Average, and

Linear Regression, in forecasting stock prices.

Because of its ability to recognise long-term

dependencies and non-linear patterns in sequential

data, LSTM networks, a type of recurrent neural

networks, have become highly effective in time series

forecasting. Moving Average, on the other hand, is a

simple and widely used method that calculates the

average of a certain number of previous stock prices

to make predictions. Linear Regression, a classical

statistical technique, fits a linear equation to historical

price data to estimate future prices. Performance

measures like Mean Squared Error (MSE) and R-

squared are used to assess these approaches. The

accuracy of the model is demonstrated by the MSE,

which calculates the average squared difference

between the anticipated and actual stock values. The

percentage of variance in the stock prices and

predictors represented by the R-squared number

indicates how well the model fits the data. By

comparing the performance of these methods, we aim

to identify the most effective approach for stock price

prediction. The findings of this study can contribute

to the field of financial forecasting, providing

valuable insights for investors and financial

professionals in their decision-making processes.

Furthermore, it offers insights into the effectiveness

of different prediction techniques. By comparing the

performance of LSTM, Moving Average, and Linear

Regression, investors and financial professionals can

gain a better understanding of the most suitable

approach for forecasting stock prices. During the

stock price prediction process using the code

provided, various algorithms or models are

considered and evaluated. Firstly, the data is pre-

processed using a MinMaxScaler to bring them

176

Amarendra, C., Parimala, K., Shivateja, R., Vivek, B. F. and Jashuva, K.

Comparative Analysis of Stock Price Prediction Models.

DOI: 10.5220/0013909800004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 4, pages

176-181

ISBN: 978-989-758-777-1

within a specific range. Each algorithm is trained on

the pre-processed data to learn the patterns and

relationships between stock prices. Subsequently, the

trained models are tested on a dataset to assess their

performance and accuracy in predicting stock prices.

Evaluation metrics such as Mean Squared Error

(MSE) and R-squared are utilized to quantify the

performance of each algorithm. The remainder of the

paper is divided into the following sections. There is

a comprehensive literature review in Section II. The

methodology is explained in Section III. A dataset that

was utilised in our studies is provided in Section IV,

together with a thorough analysis of the outcomes,

which compares the effectiveness of the various

models. The implications of our conclusions are

covered in Section V. Finally, Section VI summarises

our findings and provides potential directions for

further investigation.

2 LITERATURE SURVEY

In recent years, stock price prediction has attracted

significant attention in the field of finance and

machine learning. Researchers have explored various

techniques, including Long Short-Term Memory

(LSTM) models, to capture the complex dynamics of

stock market data and improve forecasting accuracy.

Cheung and Chong (1995) used support vector

machines and moving averages to empirically analyse

stock prices. They investigated how well these

techniques predicted changes in stock prices.

According to the study’s findings, moving average

and support vector machines can give investors

important information about short-term stock price

patterns and aid in their decision-making.

Hochreiter and Schmidhuber (1997) introduced

LSTM models as a powerful tool for learning and

retaining long term dependencies in sequential data.

Their significant work laid the foundation for

LSTM’s application in various domains, including

stock price prediction.

Fabozzi, Focardi, and Kolm (2012) presented a

com prehensive book on financial econometrics,

covering various modelling techniques for analysing

financial data. The book provides a comprehensive

overview of the basics and advanced concepts in

financial econometrics, including the application of

statistical methods like moving averages and

regression models for forecasting stock prices.

Al-Yaseen and Sathasivam (2019) proposed a

novel time series prediction algorithm utilizing

LSTM models for stock market forecasting. Their

study showcased the effectiveness of LSTM models

in capturing the underlying dynamics of stock prices

and outperforming traditional approaches.

Lim and Kim (2019) investigated the application

of LSTM-based deep learning models specifically for

stock price prediction. They emphasized the

robustness and accuracy of LSTM models in

capturing complex relationships and patterns in stock

market data, highlighting the superiority of deep

learning over traditional forecasting methods.

Zhang and Li (2020) focused specifically on

forecasting stock prices using LSTM models. Their

research provided insights into the design and

hyperparameter tuning of LSTM models, leading to

improved prediction accuracy.

3 EXISTING SOLUTIONS

Traditional stock price prediction methods have relied

primarily on Linear Regression and Moving Average

techniques. Linear Regression fits a linear

relationship between past stock prices and time, but it

assumes that stock prices follow a linear trend, which

is rarely the case in the highly volatile and non-linear

nature of stock markets. Moving Average smooths,

the data by averaging prices over a period, but it

suffers from lagging and fails to adapt to rapid market

changes, resulting in inaccurate forecasts.

These conventional models struggle with:

• Inability to capture complex non-linear

dependencies.

• Poor performance on datasets with long-

term temporal dependencies.

• Susceptibility to noise and sudden market

fluctuations.

• Limited capacity to model sequential

patterns in financial time-series data.

Due to these limitations, there is a significant gap

in developing models capable of learning and

adapting to the dynamic and stochastic behaviour of

stock prices.

4 PROPOSED SOLUTIONS

To overcome the shortcomings of traditional models,

the proposed solution leverages a Long Short-Term

Memory (LSTM) Neural Network for stock price

prediction. LSTM is designed to handle sequential

and time-series data, making it suitable for stock

market forecasting. LSTM can capture long-term

dependencies, retain useful information over

Comparative Analysis of Stock Price Prediction Models

177

extended periods, and effectively model non-linear

relationships between variables.

The proposed LSTM-based approach provides:

• Superior prediction accuracy by learning

patterns that span longer timeframes.

• Better handling of non-linearity and

volatility present in financial markets.

• Memory cells and gating mechanisms that

prevent vanishing gradient problems,

common in traditional RNNs.

• Reduction of prediction errors as

demonstrated by lower Mean Squared Error

(MSE) and higher R-Squared (R²) values

compared to Linear Regression and Moving

Average.

By adopting LSTM, the system achieves a more

reliable and efficient stock price prediction model,

suitable for practical financial decision-making.

5 METHODOLOGY

5.1 Moving Average

A typical stock indicator in technical analysis is the

moving average. By producing a continuously

updated average price, the moving average of a stock

is calculated to in smoothing out the price data and

enabling rice data and enable analysts to see trends

and patterns. The moving average generates a

smoothed line that where represents the mean price

across a defined time frame. Traders and analysts use

it to identify stock market trends. For example, When

the present market value exceeds the moving average,

it may signal an ascending trend, whereas a price

falling below the moving average could indicate a

descending trend. Additionally, many traders utilize

the intersection of various moving averages as a

method to generate trading cues. For instance, the

intersection of a brief-term moving average rising

above an extended-term moving average might be

interpreted as a positive market signal, potentially

indicating a favourable moment for investment.

𝑀𝐴 =

∑

        

  

(1)

The limitations of this moving average are lagging

indicators because they are based on historical price

data, sensitivity to timeframes as different timeframes

can produce varying moving average results, rely on

price data and do not take into account other critical

factors that influence the stock market, such as

fundamental analysis, news events, economic indica

tors, and investor sentiment, in volatile or choppy

markets with frequent price fluctuations and no clear

trend that may generate false or conflicting signals,

These calculations rely on past data, which may not

accurately represent present or upcoming market

trends.

5.2 Linear Regression

Linear regression is a statistical technique commonly

used for stock market predictions. It involves fitting a

straight line to historical price data to estimate future

price movements. Linear regression is a relatively

simple and straightforward statistical technique. It is

easy to understand and implement, making it

accessible to both beginners and experienced

analysts. It provides interpretable results. This model

is trained and applied quickly, allowing for rapid

analysis and prediction. Linear regression can help

identify relevant independent variables that influence

stock price movements. By examining the

coefficients, analysts can determine which variables

have a significant impact on the target variable, aiding

in feature selection and model refinement.

𝑦 = 𝛽0 + 𝛽1𝑥1 + 𝛽2𝑥2 +··· +𝛽𝑛𝑥𝑛 (2)

The target variable and the independent variables

are assumed to have a linear relationship using linear

regression. However, stock market data often exhibits

nonlinear patterns and complexities, which may limit

the accuracy of predictions using linear regression

alone. To enhance predictions, additional techniques

such as polynomial regression, time series analysis,

or machine learning algorithms can be employed to

capture nonlinear relationships and incorporate more

sophisticated modelling approaches.

5.3 LSTM

The purpose of LSTMs is to capture long-term

dependencies and patterns in sequential data. Unlike

moving averages and linear regression, which do not

inherently consider the sequential nature of the data,

LSTMs can learn from the historical sequence of

stock prices and capture complex temporal

relationships. Stock price movements often exhibit

nonlinear patterns, which can be challenging to

capture with linear regression. LSTMs, with their

ability to model complex nonlinear relationships, can

capture the intricate dynamics of the stock market by

leveraging the memory cells and gating mechanisms

within the LSTM architecture. Moving averages and

linear regression often rely on a limited set of

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

178

features, such as historical prices or technical in

dicators. LSTMs have the capability to automatically

identify and extract relevant features from raw data

inputs. This allows them to potentially uncover more

subtle and meaningful patterns that may not be

immediately obvious or captured by alternative

methods. LSTMs have an advantage over simple

moving averages and linear regression when dealing

with long-term dependencies. They are equipped with

memory cells that can store and recall information

over extended time periods, allowing them to capture

dependencies that occurred further back in time,

which is particularly valuable for stock price

prediction. LSTMs A. Data Preprocessing can adapt

and learn from changing market conditions by

continuously updating their weights and biases during

training. This adaptability enables the model to adjust

to new patterns and trends in the stock market,

making it more robust to evolving market dynamics

compared to fixed formulas like moving averages or

linear regression. Unlike fixed length moving

averages or regression models, LSTMs can handle

sequential data of varying lengths. This flexibility is

essential in stock price prediction, as historical price

data may have different time spans, irregular

intervals, or missing data points. LSTMs can

incorporate additional contextual information, such

as news sentiment, market indicators, or

macroeconomic factors, alongside historical price

data. This broader set of input features allows the

model to capture more comprehensive information

and potentially improve prediction accuracy. Figure 1

shows the workflow of LSTM whereas Figure 2

shows the Moving Average and Linear Regression.

Figure 1: Workflow of LSTM.

Figure 2: Workflow of moving average and linear

regression.

6 EXPERIMENTAL RESULTS

6.1 Data Set Summary

The data set includes columns for date, which

includes the open and close dates for stock market

data. When trading begins, the stock’s initial price;

during the trading session, the stock’s maximum

value attained; throughout the trading period, the

stock’s minimum value reached; and at the conclusion

of trading, the stock’s final price, as well as volume,

or the total number of shares or contracts exchanged

on the day. The dataset’s Open column was chosen as

the target variable for processing and training the

LSTM model, which was then used to the test set to

provide predictions.

6.2 Evaluation Metrics

Mean Squared Error (MSE) computes the average of

the squared disparities between predicted and actual

values. This metric assesses the overall prediction

error, with lower MSE scores indicating higher

prediction accuracy.

𝑀𝑆𝐸 = (1/𝑛) ∑(𝑦



−𝑦



(3)

where n is the total number of predictions, y

predict

is the predicted value, and y

actual

is the actual value.

R-Squared calculates the share of the model’s

independent variables (predictors) that can be used to

explain the variance in the dependent variable (stock

market values). It indicates how well the model fits

the information.

𝑅



= 1 − (𝑅𝑆𝑆/𝑇𝑆𝑆) (4)

Where TSS and RSS are given by

𝑇𝑆𝑆 = ∑(𝑦



,𝑖−𝑦)2 (5)

Comparative Analysis of Stock Price Prediction Models

179

𝑅𝑆𝑆 = ∑(𝑦



,𝑖− 𝑦



,𝑖)2

(6)

ranges from 0 to 1, where a value of 0 means

that the model explains no variation and a value of 1

means that it fits the data perfectly. Higher R

values

show a better fit between the model and the data.

Table 1: Evaluation of Models on JP Morgan Stock Price

Dataset.

Method MSE R Square

Linear Regression 56.8002 0.8638

Moving Average 175.4034 0.6037

LSTM 27.9309 0.9369

Table-1 shows that LSTM performs best with the

lowest MSE of 27.9309 and the highest R-Square of

0.9369, indicating strong predictive accuracy. Linear

Regression performs moderately, while the Moving

Average method has the highest MSE and lowest R-

Square, making it the least effective. These results

highlight the advantage of deep learning models for

stock price forecasting.

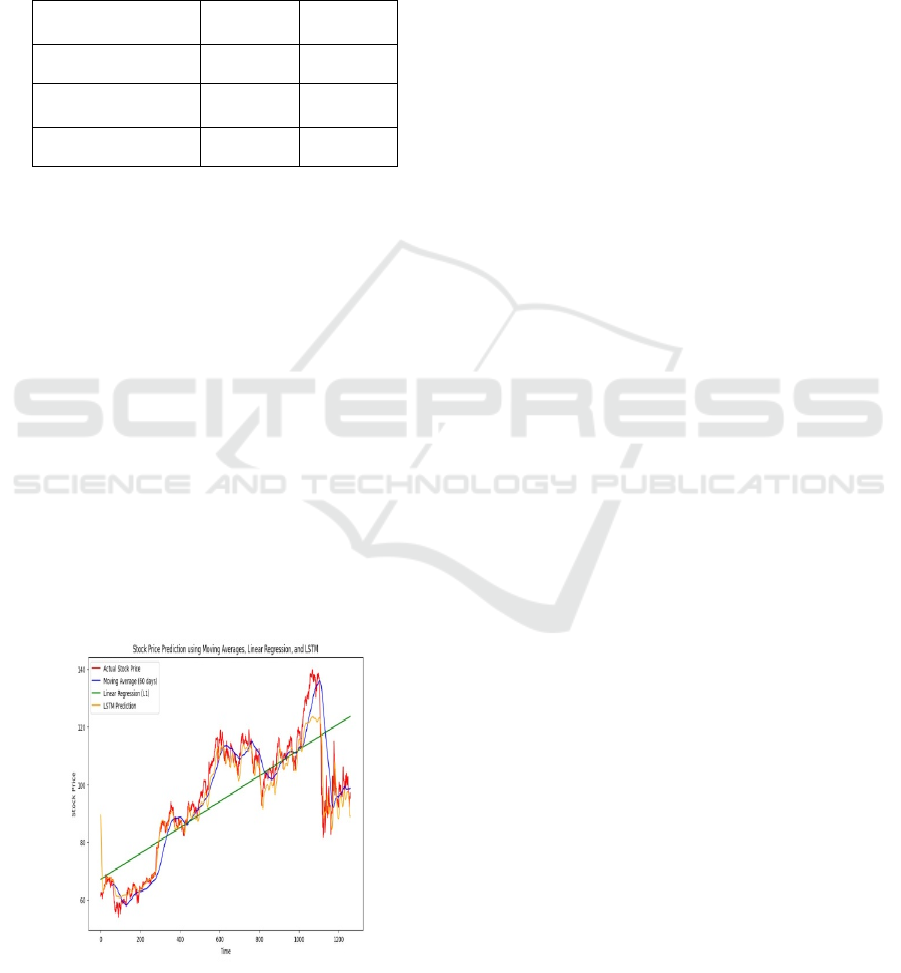
Figure 3 visualizes stock price predictions using

Moving Averages, Linear Regression, and LSTM

models. The actual stock price (red) shows high

volatility, while the Moving Average (blue) smooths

fluctuations but lags behind trends. Linear Regression

(green) provides a simple upward trend but fails to

capture variations. The LSTM model (orange) closely

follows actual stock movements, demonstrating its

ability to learn complex patterns. This aligns with

Table-1, where LSTM had the lowest MSE and

highest R-Square, confirming its superior predictive

accuracy.

Figure 3: Stock price prediction using moving average,

linear regression, and LSTM.

7 DISCUSSIONS AND

CONCLUSIONS

Sentiment analysis is beneficial for stock price

prediction because it helps capture the influence of

investor sentiment and market psychology on stock

prices. Monitoring Social Media Sentiment:

Sentiment analysis can track and analyse sentiment

expressed on social media platforms such as Twitter,

Reddit, or Stock Twits. By monitoring relevant

hashtags, company mentions, and discussions related

to the upcoming earnings report, sentiment analysis

algorithms can assess the overall sentiment expressed

by retail investors and traders. Positive sentiment may

indicate optimism about the company’s performance,

while negative sentiment may suggest concerns or

pessimism. The performance of the LSTM model can

be fine-tuned by optimizing its hyperparameters. To

determine the ideal set of parameters, methods like

grid search or Bayesian optimisation might be used,

such as the number of LSTM units, dropout rate, and

learning rate. This process can lead to further

improvements in prediction accuracy. Exploring

additional relevant features such as trading volume,

historical trends, and news sentiment can potentially

improve the predictive power of the model.

Incorporating these features into the model can

capture more nuanced patterns and enhance the

accuracy of stock price predictions.

In this study, we explored various stock price

prediction techniques using the JPMorgan stock price

dataset. We implemented Moving Averages, Linear

Regression, and Long Short-Term Memory (LSTM)

models to forecast future stock values. While Moving

Averages provided a simple trend analysis and Linear

Regression established a linear relationship with time,

the LSTM model outperformed both by capturing

complex temporal dependencies in stock prices. Our

results highlight the effectiveness of deep learning for

financial forecasting, demonstrating that LSTM

models offer more accurate predictions by leveraging

sequence modeling and historical patterns.

REFERENCES

A. Merchant, N. Shenoy, A. Bharali, and A. M. Kumar,

“Identifying Similar Questions in the Medical Domain

Using a Fine-tuned Siamese BERT Model,” in Proc.

IEEE India Council Int. Conf. (INDICON), 2022.

C. Werner, J. Voigt, S. Khattak, and G. Fettweis,

“Handover Parameter Optimization in WCDMA using

Fuzzy Controlling,” in Proc. IEEE Int. Symp. Personal,

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

180

Indoor and Mobile Radio Communications, 2007, pp.

1–6.

C. Peng, Z. Yin, X. Wei, and A. Zhu, “Stock Price

Prediction based on Recurrent Neural Network with

Long Short-Term Memory Units,” in Proc. Int. Conf.

Engineering, Science, and Industrial Applications

(ICESI), 2019.

E. Hirata and T. Matsuda, “Forecasting Shanghai Container

Freight Index: A Deep Learning-Based Model

Experiment,” Journal of Marine Science and

Engineering, 2022.

F. J. Fabozzi, S. M. Focardi, and P. N. Kolm, Financial

Econometrics: From Basics to Advanced Modeling

Techniques. Hoboken, NJ: John Wiley & Sons, 2012.

G. Zhang and B. Li, “Forecasting stock prices with a long

short-term memory recurrent neural network,” Expert

Systems with Applications, vol. 140, Article 112867,

2020.

G. Panda, B. Majhi, and S. Ghosh, “Deep learning models

for stock market prediction: A comprehensive

analysis,” International Journal of Computational

Science, vol. 12, no. 1, pp. 75–87, 2021.

J. Liu, Y. Luo, and Y. Xia, “Deep learning for stock

prediction using numerical and textual information,” in

Proc. IEEE/WIC/ACM Int. Conf. Web Intelligence

(WI), 2017, pp. 301–306. [5] V. Sharma and A. Kumar,

“Stock price prediction using LSTM, RNN and CNN-

sliding window model,” in Proc. Int. Conf. Computing,

Communication and Automation (ICCCA), 2017, pp.

1–6.

K. C. Cheung and T. T. Chong, “Empirical analysis of stock

prices using moving average and support vector

machines,” in Proc. Int. Joint Conf. Neural Networks,

vol. 2, 1995, pp. 1363–1366.

M. Gholamzadeh and A. Amindoust, “Application of

LSTM Neural Network for Stock Price Prediction: A

Comparative Analysis,” Sensors, vol. 21, no. 18,

Article 6255, 2021.

M. Shahzad, F. Azam, A. Hussain, Q. Abbas, and M.

Shabbir, “Short Term Stock Price Prediction Using an

Integrated Deep Learning Ap proach,” Signal

Processing, 2021, Article 4055281.

M. Shahin, F. F. Chen, A. Hosseinzadeh, and N. Zand,

“Using Machine Learning and Deep Learning

Algorithms for Downtime Minimization in

Manufacturing Systems: An Early Failure Detection

Diagnostic Service,” Research Square Platform LLC,

2023.

S. Hochreiter and J. Schmidhuber, “Long short-term

memory,” Neural Computation, vol. 9, no. 8, pp. 1735–

1780, 1997.

W. N. Al-Yaseen and S. Sathasivam, “Forecasting stock

market prices using a novel time series prediction

algorithm,” Expert Systems with Applications, vol.

132, pp. 245–259, 2019. [10] S. Y. Lim and J. H. Kim,

“Predicting stock prices using LSTM-based deep

learning models,” Sustainability, vol. 11, no. 5, Article

1319, 2019.

Comparative Analysis of Stock Price Prediction Models

181