(One, Two) Tri Vertex Domination in Fuzzy Graphs

Kavitha T., Tharani S. and Deepa R.

Department of Mathematics, E.G.S. Pillay Engineering College, Nagapattinam, 611002, Tamil Nadu, India

Keywords: (1, 2) Dominating Set in a Fuzzy Graph, (One, Two) Tri Vertex Domination Number in a Fuzzy Graph.

Abstract: Sarala.N and Kavitha.T has established the concept of triple connected domination in fuzzy graph. In this

paper we introduce the (One, two) tri-vertex domination number in fuzzy graph and present several intriguing

findings regarding this new parameter domination in fuzzy graphs.

1 INTRODUCTION

Mahadevan G and Selvam A created the notion of

triple-connected domination in graphs. In this study,

we investigate the limitations on the (One, two) tri-

vertex domination number in fuzzy graph and provide

various interesting insights about this innovative

parameter domination in fuzzy graphs.

2 PRELIMINARIES

Definition 2.1: Let G (a, b) be a fuzzy graph, then is

said to be a fuzzy dominating set of G, if for each v ±

V(G), where v∈V-D, There is an u in D such that

b(u,v) = a (u) a (v). There exists a u in D with

b(u,v) = a (u) a (v). The dominant fuzzy number is

representing by 𝛾(G) is the minimum scalar order of

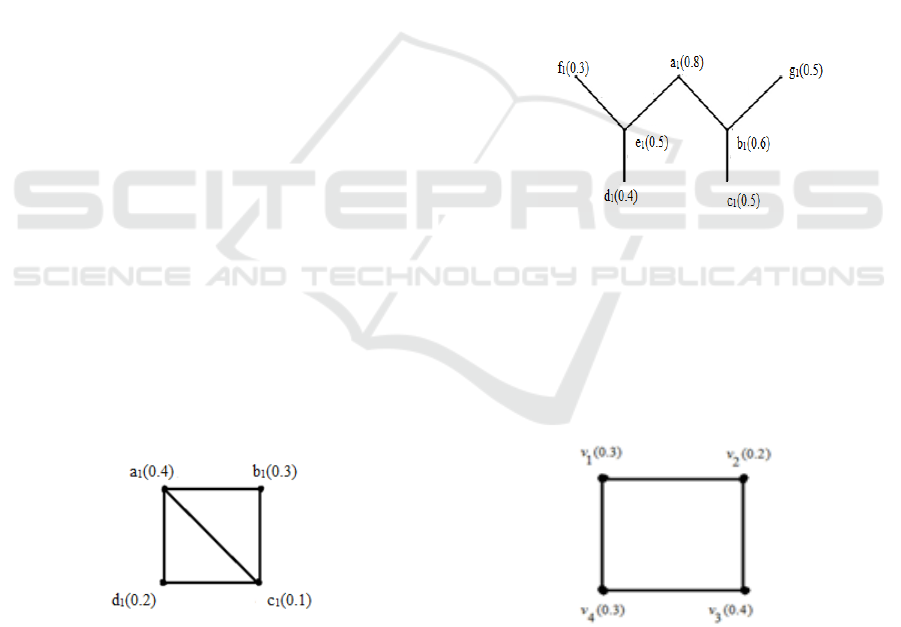
Figure 1: 𝐷=



𝑎1



, 



𝐺



=4.

Definition 2.2: A subset D of V of a non-trivial

connected fuzzy graph G is referred to be triple

connected dominating set. If D is the dominating set

and the induced fuzzy sub graph <D> is triple

connected. The minimum cardinality of all tri

connected dominating set of G is called the triple

connected dominating number of G and is denoted by

(G).

Figure 2: 





𝑎1, 𝑏1, 𝑒1



, 





𝐺



= 0.8 + 0.5 + 0.6 = 1.9

Definition 2.3: A (1,2) dominant set in a fuzzy graph

G (V, E) is a set S with the characteristic that for every

vertex v in V - S. There is at least one vertex in S that

is one distance from v, and another that is nearly two

distances away. (1,2). The minimum cardinality of a

dominating set in a fuzzy graph G is known as the

(1,2) dominance number, denoted by ϒ(1,2).

Figure 3: (1,2) dominant set ϒ(1,2)=0.7

T., K., S., T. and R., D.

(One, Two) Tri Vertex Domination in Fuzzy Graphs.

DOI: 10.5220/0013893300004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 3, pages

139-142

ISBN: 978-989-758-777-1

139

3 (ONE, TWO) TRI VERTEX

DOMINATION IN FUZZY

GRAPHS

In this section, we introduce several basic limits on

(One, two) tri vertex domination within fuzzy graphs.

The concept of (One, two) tri vertex domination

revolves around tri vertices. It is represented by ϒ

(One, two) along with related findings.

Definition 3.1: A (One, two) tri vertex dominant

set in a fuzzy graph G (V, E) is defined as a set S such

that for every vertex v in V - S, there are at least three

vertices in S that are one distance away from v, as

well as a second vertex in S that is almost two

distances away from v. The smallest size of a (One,

two) tri vertex dominating set in a fuzzy graph G is

known as the (One, two) tri vertex dominance

number, denoted by ϒ

(One, two).

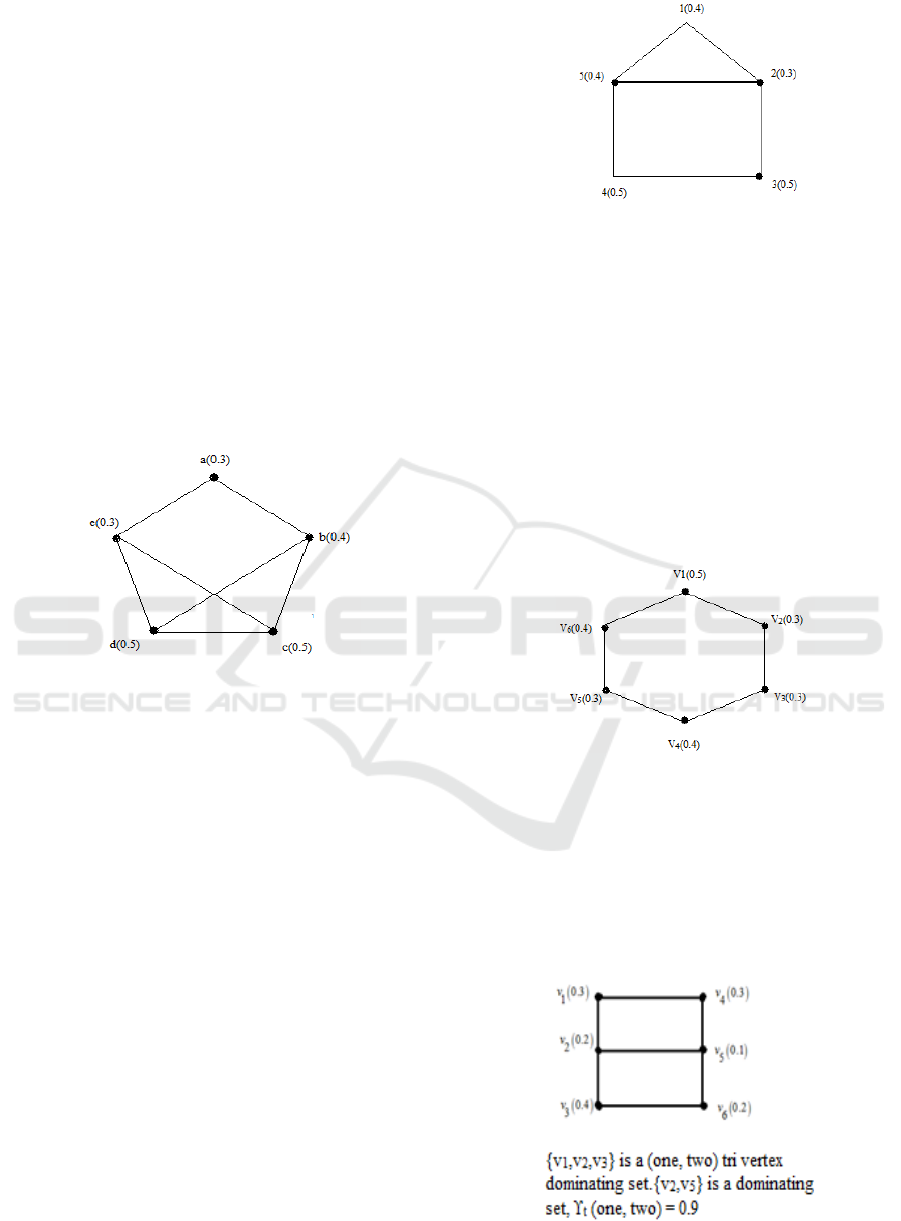
Figure 3.

Here (One, two) tri vertex dominating set is {b,c,d},

(One, two)=1.4

Theorem 3.2: (One, two) tri-connected dominating

set for fuzzy graphs does not exist for all cases.

Proof: According to definition 3.1, if there are fewer

than three dominating vertices, the connected graph

cannot be considered tri-connected. We will focus

only on connected fuzzy graphs that have a

dominating set consisting of one or two vertices.

Theorem 3.3: The complement of a (One, two) tri

vertex dominating set is not necessarily a (One, two)

tri vertex dominating set.

Proof: For the fuzzy graph G, the set D serves as a

(One, two) tri vertex dominating set of G, while the

complement V-D does not qualify as a (One, two) tri

vertex dominating set.

Example 3.4: For the fuzzy graph G in Fig:4, (One,

two) tri vertex dominating set D= {1,3,4} and V-D=

{2,5} is not (One, two) tri vertex dominating set

Figure 4.

Theorem: 3.5: Every (One, two) tri vertex

dominating set qualifies as a dominating set, but the

reverse is not necessarily true.

Proof: According to the definition of a (One, two) tri

vertex dominating set, if D is a subset of V, then D

constitutes a tri vertex dominating set of G, which

means it is also a dominating set. However, it is

important to note that not every dominating set must

be a (One, two) tri vertex dominating set.

Example 3.6: For the fuzzy graph G in Fig:5, (One,

two) tri vertex dominating set = {v

, v

} and

dominating set D= {v

, v

} but dominating set is need

not to be a (One, two) tri vertex dominating set.

Figure 5.

We look at ladder fuzzy graphs of orders 3 to 5

and find their domination number as well as the

domination number of (One, two) tri vertex. The

ladder fuzzy graph (Ln) is harmonious. This fuzzy

graph resembles a ladder, with two rails and n rungs

connecting them.

For n are three

For n are four

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

140

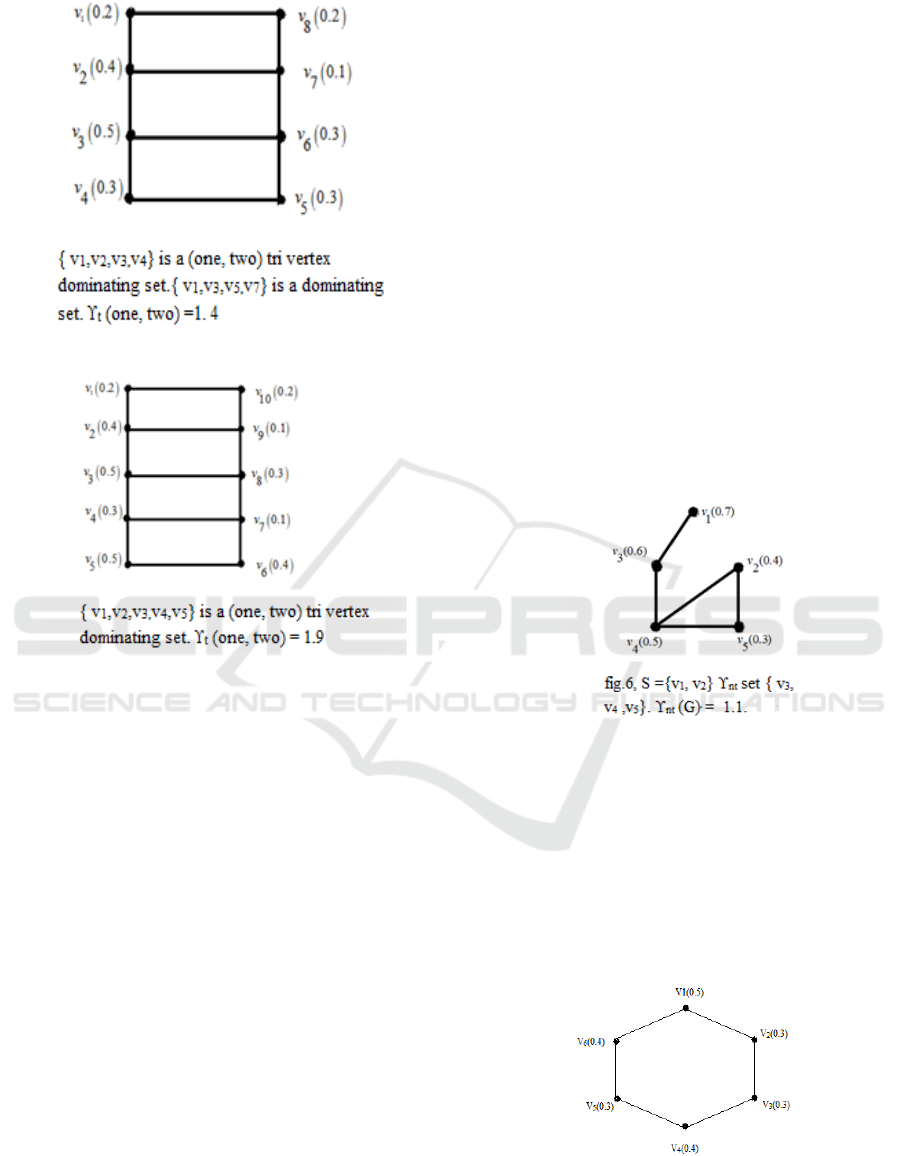
For n are five

From the cases above, we obtain the following

theorems:

Theorem 3.7: (One, two) tri vertex dominating

vertices is n for a ladder fuzzy graph.

Proof: In ladder fuzzy graph, twice of n vertices and

thrice of n vertices minus two edges also both rails

have n vertices. Assume that the right hand vertex in

the first rail is adjacent to left hand vertex in the

second rail. The other vertices in the first rail will be

at a distance greater than one from first left hand

vertex to build a (One, two) tri vertex dominating set;

we must include all of the vertices in a single rail and

connect at least three vertices. So the (One, two) tri

vertex dominating vertices are n

Theorem 3.8: (One, two) tri vertex dominating

vertices is n for a ladder fuzzy graph with n even

Proof: In ladder fuzzy graph, twice of n vertices and

thrice of n vertices minus two edges. If n is even, the

vertex in the inner rungs (n/2 rungs) can form a

dominant set. As each rung contains two vertices, the

dominating set will have n vertices.

4 (ONE, TWO)

NEIGHBOURHOOD TRI

VERTEX DOMINATION IN

FUZZY GRAPHS

In this part, we discuss fundamental constraints on

(One, two) Neighbourhood tri vertex domination in

fuzzy graphs. The idea behind (One, two)

Neighbourhood tri vertex domination revolves

around three Neighbourhood vertices. It is

symbolized as ϒ

(One, two) together with related

findings.

Definition 4.1: A subset S of V of a fuzzy graph G is

called to be a Neighbourhood triple Connected

dominating set, if S is a dominating set and the

induced sub graph < N(S) > is triple connected. The

minimum cardinality of all Neighbourhood triple

connected dominating sets is known as the

Neighbourhood triple connected dominance number.

Definition 4.2: A (One, two) Neighbourhood tri

vertex dominant set in a fuzzy graph G (V, E) is

defined as a set N(S) such that for every vertex v in V

- N(S), there are at least three vertices in N(S) that are

one distance away from v, as well as a second vertex

in N(S) that is almost two distances away from v. The

smallest size of a (One, two) Neighbourhood tri

vertex dominating set in a fuzzy graph G is known as

the (One, two) Neighbourhood tri vertex dominance

number, denoted by ϒ

(One, two).

Figure 6: (One, Two) Tri Vertex Dominating Set ={V1,

V4,V6} ,Dominating Set D= {V1,V4 } and (One, Two)

Neighbourhood Tri Vertex Dominating Set ={ V2,V3,V5}.

(One, Two) Tri Vertex Domination in Fuzzy Graphs

141

Observation 4.3: (One, two) neighbourhood tri

dominating set for fuzzy graph does not exist for all

cases

Observation 4.4: The complement of a (One, two)

neighbourhood tri dominating set is not necessarily

a (One, two) neighbourhood tri dominating set.

Observation 4.5: Every (One, two) neighborhood tri

dominating set qualifies as a dominating set, but the

reverse is not necessarily true.

5 CONCLUSIONS

(One, two) tri vertex dominance in a fuzzy graph is

defined, as is (One, two) neighbourhood tri vertex

dominating set. Theorems and observations about this

notion are derived, and the relationship between

dominance number in a fuzzy graph and (one, two)

and neighborhood tri vertex domination in fuzzy

graphs is established.

REFERENCES

Bhattacharya, Some remarks on fuzzy graphs, Pattern

Recognition letter 6,297-302.

Haynes T W, Hedetniemi S T and Slater P J, Fundamentals

of domination in Graphs, Marcel Dekker,New York,

1998.

Innovative Research in Science, Engineering and

Technology, Vol 5, Issue 9 (2016) 16501-16505

Mahadevan G and Selvam, (1, 2) - Domination in Graphs.

Murugesan N. and Deepa S. Nair, The Domination and

Independence of Some Cubic Bipartite Graphs, Int. J.

Contemp. Math Sciences, Vol.6, 2011, No.13,611-618.

Murugesan N and Deepa S Nair, (1,2) - domination in

Graphs,J. Math.Comput. Sci., Vol.2, 2012, No.4, 774-

783.

Rosenfeld A, Zedeh L A, Fu.K.Tanaka K S , Fuzzy sets and

their Application to cognitive and Decision processes

,Academic press, Newyork (1975) ,77-95.

Sarala N, Kavitha T,Connected Domination Number of

Square Fuzzy Graph ,IOSR-JM,Volume10, Issue 6 Vel

III (2014), 12-15

Sarala N,Kavitha T,Triple connected domination number of

fuzzy graph, International Journal of Applied

Engineering Research, Vol. 10 No.51 (2015)914-917

Sarala N,Kavitha T,Neighbourhood and efficient tri

connected domination number of a fuzzy graphIntern.

J. Fuzzy Mathematical Archive Vol. 9, No. 1, 2015, 73-

Sarala N, Kavitha T, Strong (Weak) Tri Connected

Domination Number of a Fuzzy Graph, International

Journalof Computational Engineering Research,

Volume, 05 Issue, 11 2015 ,18-22

Sarala N,Kavitha T,(1,2) vertex domination number in

fuzzy graph, International Journal of

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

142