Efficient Three Operand Adder Design with Carry Prefix Logic for

Reduced Delay

Divya S

, Mohankumar M

, Dhanasekar J

, Krishnaraj R

, T. Senthil

and Vikram N

VLSI Design, Sri Eshwar College of Engineering, Coimbatore, Tamil Nadu, India

Department of Electronics and Communication Engineering, Sri Eshwar College of Engineering, Coimbatore,

Tamil Nadu, India

Department of Electronics and Communication Engineering, Bannari Amman Institute of Technology, Sathyamangalam,

Tamil Nadu, India

Department of Computer Science and Engineering, Sreenivasa Institute of Technology and Management Studies, Chittoor,

Andhra Pradash. India

Department of Electronics and Communication Engineering, Sona College of Technology, Salem, Tamil Nadu, India

Keywords: Carry Save Adder (CSA), Three-Operand Binary Adder, Han-Carlson Adder (HCA), Low Power, and High

Speed.

Abstract: Cryptography and pseudorandom number generators are essential tools from the modern digital world. For

performance improvement adder implementations like (CS3A) and (HCA) are frequently employed. But

these adders exhibit high propagation delays that reduce the efficiency of the system. A new three-operand

binary adder architecture is presented that utilizes carry-prefix logic to achieve low power and propagation

delay. The design below obtains a log₂n time complexity via pre-computed bitwise addition, followed by a

carry-prefix compute. The proposed design was implemented with Xilinx ISE 14.7, showing that it is

power efficient and less delay-centric than CS3A and HCA adders. These results attest to the fact that the

proposed architecture can be utilized to enhance the performance of a digital system.

1 INTRODUCTION

An adder is a basic digital circuit that adds numbers,

and is a crucial building block in processors and

arithmetic logic units (ALUs). Its importance

extends to functions like address computation, table

index generation or incrementing and decrementing

in numerous digital architectures. A well-known

type of adder is the Binary Adder which can use

simple gates like AND and XOR to implement. The

type of adder we will be using adds two single-bit

binary numbers together, outputting both a carry-out

(COUT) bit as well as the sum. The Binary Adder

uses the forumal of binary additions, where sum of

any two bits will generate carry or a sum. In modular

arithmetic, frequently used in cryptographic

algorithms and pseudo-random bit generator

(PRBG) techniques, the CS3A method is one of the

most space-efficient and commonly used methods to

add three operands. The CS3A method adopts the

PP2A method, which is similar in structure to the

HCA, to new outweighing time of the critical path.

The compact design is essential for VLSI (Very

Large Scale Integrated) circuits as it enables binary

addition over three operands whilst consuming little

hardware. Such optimization is needed since they

will need to run the fastest and most space-wise

regardless of whether they are cryptographic

applications or any other digital systems.

2 LITERATURE REVIEW

CSCM: A Carry Save Adder (CSA) design reducing

power and delay. The CSA design is optimized to

address key path delays and energy efficiency

issues. The proposed method enhances performance

metrics compared to traditional CSA designs

through a systematic design review and

enhancement process. The results indicate that the

enhanced CSA is suitable for computational

processes that need less power and high speed

Divya, S., Mohankumar, M., Dhanasekar, J., Krishnaraj, R., Senthil, T. and N., V.

Efﬁcient Three Operand Adder Design with Carry Preﬁx Logic for Reduced Delay.

DOI: 10.5220/0013890100004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 2, pages

795-799

ISBN: 978-989-758-777-1

795

(Krishna Vamsi, et, al 2018) Adiabatic logic is used

for high-speed arithmetic operations that provide

acceptable performance at lower power operating;

(Nagesh N, et, al, 2018) which not only guarantees

low energy dissipation during the entire addition

process, but also helps to reduce the operation delay.

In this proposed architecture, energy consumption

and performance are optimized by using different

adder types to perform the addition of wide

operands (Jafarzadehpour, A, et, al, 2019). By

combining Transmission Gate Logic (TGL) and

CMOS we maximize the size, delay and power

consumption in hybrid architecture. This approach

avoids the drawbacks of classical RCAs through

enhanced speed and minimized power dissipation.

This indicates that the design can be used for low-

power purpose applications and offers an improved

performance over traditional methods. (Bagwari, A,

et, al, 2019). This design would optimize the carry

generation and propagation structure to speed up a

parallel prefix adder. For large operand sizes, this

architecture provides a speedup for addition overall,

as the latency of the critical path is significantly

reduced. The proposed adder is quicker than

traditional adder architectures, making it suitable for

demanding applications where high-speed

arithmetic processing is crucial (Knowles, S, et, al,

2001).

3 16 BITS THREE - OPERAND

BINARY ADDER

This section presents a new adder architecture for

adding three operands in modular arithmetic and its

corresponding VLSI implementation. The proposed

adder is a Parallel Prefix Adder (PPA) with a four-

stage structure, unlike a traditional prefix adder,

which follows a three-stage structure. There are four

stages of the adder: bit-addition logic, basic logic,

carry prefix logic, and sum logic. The first stage of

the bit-addition logic stage adds the three n-bit

binary input operands bit by bit via an array of full

adders. The full adder generates two outputs, C

(carry) and S (sum). In this step, each complete

adder will perform the addition of the bits a, b, and c

(the previous carry that is coming from 1 or 0) and

the next input bits will be executed at the basic logic

stage, so that they can prepare the operands for the

carry and propagate these findings. Stage 2:

Fundamental Logic Stage. During this stage,

generate and propagate signals are calculated. This

processing of the output signals of the full adders

(from the preceding stage). In particular, the sum

from the full adder and the carry of the full adder to

the right. We use the squared saltire-cell to illustrate

these calculations. The calculation of both generate

and propagate signals use this saltire-cell structure (n

+ 1 saltire-cells in the base logic stage). The method

aids in speeding up the carry propagation and the

sum calculation during the addition of three

operands in modular arithmetic applications and

helps provide faster VLSI design with minimum

space and time complexity.

Gi: i = Gi = Si · Cyi − 1 (1)

Pi: i = Pi = Si ⊕ Cyi − 1 (2)

For three-operand addition, the proposed adder

algorithm additionally considers the external carry-

input signal (Cin). As you can see, in the first

saltire-cell of the base logic, this additional carry-

input signal (Cin) is collected and continues to exist

within the logic, used to calculate the G0 (S Cin ));

According to the logical equation combine the black

and grey cell logics to realize the carry generate Gi:

j, and propagate Pi: j signals in the third stage,

called the “generate and propagate logic” (PG) stage

for pre-analysis of carry bit:

Gi: j = Gi: k + Pi: k · Gk − 1: j (3)

Pi: j = Pi: k · Pk − 1: j (4)

The final phase is represented as sum logic, in

which the "sumbits from the carry create Gi:j and

carry propagate Pi bits are calculated using the

logical expression 𝑆𝑖 = (𝑃𝑖⊕𝐺𝑖−1:0). The carryout

signal is directly produced by the carry generator.

Figure 1: Block diagram of 16 bit Three operand Binary

Adder.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

796

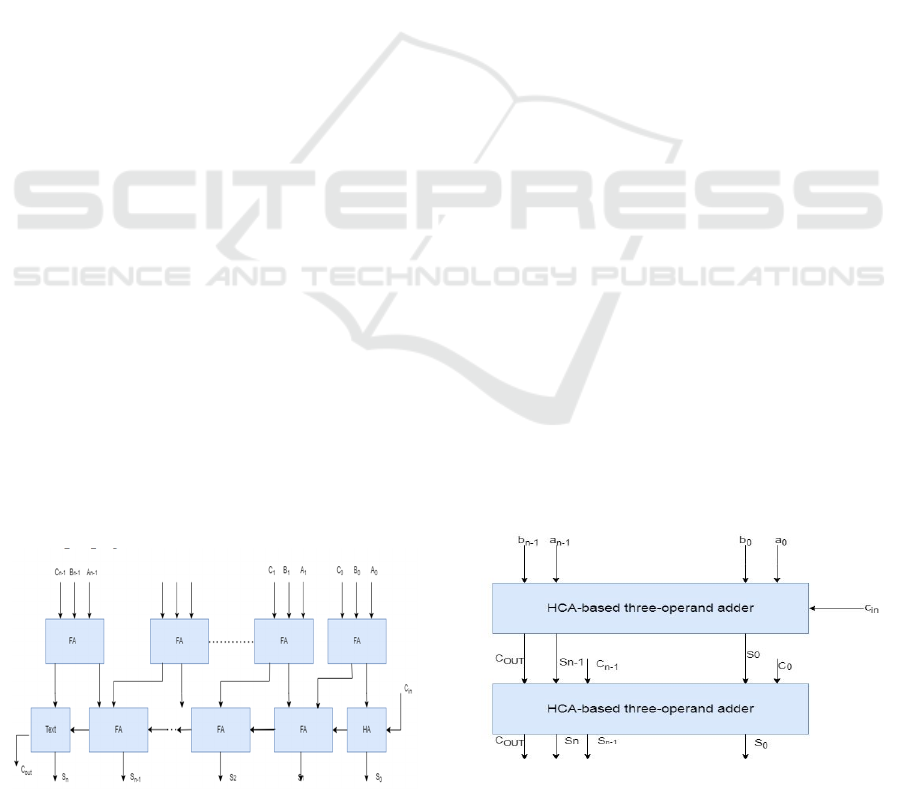
4 CARRY SAVE ADDER

A digital adder known as a carry-save adder, or

CSA, is primarily used to effectively calculate the

sum of at least three binary values. A binary

multiplier typically uses a CSA since it adds the two

binary numbers mentioned above once they have

been multiplied. This technique allows for the

implementation of a large adder, which is

significantly faster than adding numbers as is

customary. The process of adding together binary

bits involves preserving the carry and sum bits in the

first step before moving on to the second.

The stored carry and sum bits are added in this

step, which functions similarly to a ripple carry

adder, or RCA. This adder uses three operands, such

as a, b, and c, where "c" is a four-bit input carry. In

this case, all four FAs, a, b, and c are utilized. The

sum and carry bits are generated for each FA. In this

case, the carry bits are simply kept and added up to

the next sum term using a ripple carry adder rather

than being sent to the following FA.

The primary function of a carry save adder is to

calculate the sum of at least three n-bit binary

values.

A full adder and this kind of adder are

comparable. Each adder in the carry save unit

computes a single sum and carry bit based only on

the equivalent two input number bits. Assume that,

in the example below, two 4-bit values, such as a &

b, produce the partial sum "S" and carry "C."

𝑆 = 𝑎 𝑥𝑜𝑟 𝑏 𝐶 = 𝑎 𝑎𝑛𝑑 𝑏 (5)

The carry sequence "C" can be moved one position

to the left. Put a zero on the partial sum sequence

"S"'s front MSB. Ultimately, these two are added

and the final sum is produced using a ripple carry

adder, or RCA. This adder's primary job is to create

two numbers, sum "S," and carry C by adding three

k-bit integers, such as a, b, and c. While the carry

generator is used to generate the output carry

regardless of the input carry, the carry propagator is

used to propagate to the next level.

Figure 2: Block diagram of Carry save adder.

Two of the carry's functions are generation and

propagation. While the carry generator (Cg) is

employed, the carry propagation (Cp) is spread to

the next level to produce the output carry regardless

of the input carry. When calculating the sum of

several numbers, the Carry Save Adder is frequently

utilized. It conducts the final addition after storing

and transporting the partial results independently.

Although it's effective for some multi-operand

addition workloads, simple two-input addition

procedures don't usually employ it.

5 HAN-CARLSON ADDERS

Han and Carlson (1987) introduced the Han-Carlson

adder to strike a balance between the number of

computational nodes, interconnects, and logic depth

in digital adders. A network formed by combining

the Kogge-Stone and Brent-Kung adders is known

as a Han-Carlson tree. This adder applies the Brent-

Kung method for the outer rows of the prefix tree,

while using the Kogge-Stone approach for the inner

rows. When compared to the Kogge-Stone adder,

Han-Carlson prefix trees require fewer logic cells

and fewer interconnects, but at the cost of an

additional logic level for carry merging to determine

missing carries. The number of logic levels is given

by the formula [log2 (n) + 1], where "n" represents

the number of bits in the operands. Brent-Kung is

applied at the beginning and end of the prefix graph,

while the first and middle stages of the adder involve

black and grey cells positioned at odd bit positions.

In the final stage, where carry merging occurs, only

grey cells are used at the even bit positions. Overall,

the Han-Carlson adder provides a good compromise

between fan-out, the number of logic cells, and the

black cell count, making it an efficient choice

compared to the Kogge-Stone adder. The adder must

be quick and, secondly, efficient in terms of chip

area and power consumption.

Figure 3: Block level diagram of HCA-based Three-

Operand Adder (Hc3a).

Efﬁcient Three Operand Adder Design with Carry Preﬁx Logic for Reduced Delay

797

A solid theoretical foundation for creating a variety

of designs is provided by parallel prefix adders.

trade-offs between power, area, and delay. The

design is modularized by dividing it into trees of

smaller and quicker adders that are easier to

implement because the adders with the massive

complex gates will be too sluggish for VLSI. Tree

adders, or parallel prefix adders, are commonly used

in digital circuits due to their ability to reduce delay,

especially in large adders where the carry

propagation dominates. High-speed addition relies

on the prior carry to produce the correct sum. Any

reduction in latency in integer addition leads to

higher throughput. As technology scales to the

nanoscale range, it becomes increasingly important

to design addition algorithms that not only deliver

excellent performance but also consume less power.

Parallel prefix adders are particularly well-suited for

VLSI (Very Large-Scale Integration)

implementation because they use simple cells and

maintain regular connections between them, making

them efficient for high-density integration. These

adders can be described in terms of wiring tracks,

fan-out, and logic levels, all of which influence their

performance. Prefix cells are typically constructed

using complex gates, along with zero or more

inverters to buffer their outputs. CMOS technology

is commonly used to build these gates. In this design

approach, buffers are employed to manage fan-out

and reduce gate loading, as excessive fan-out can

negatively affect performance.

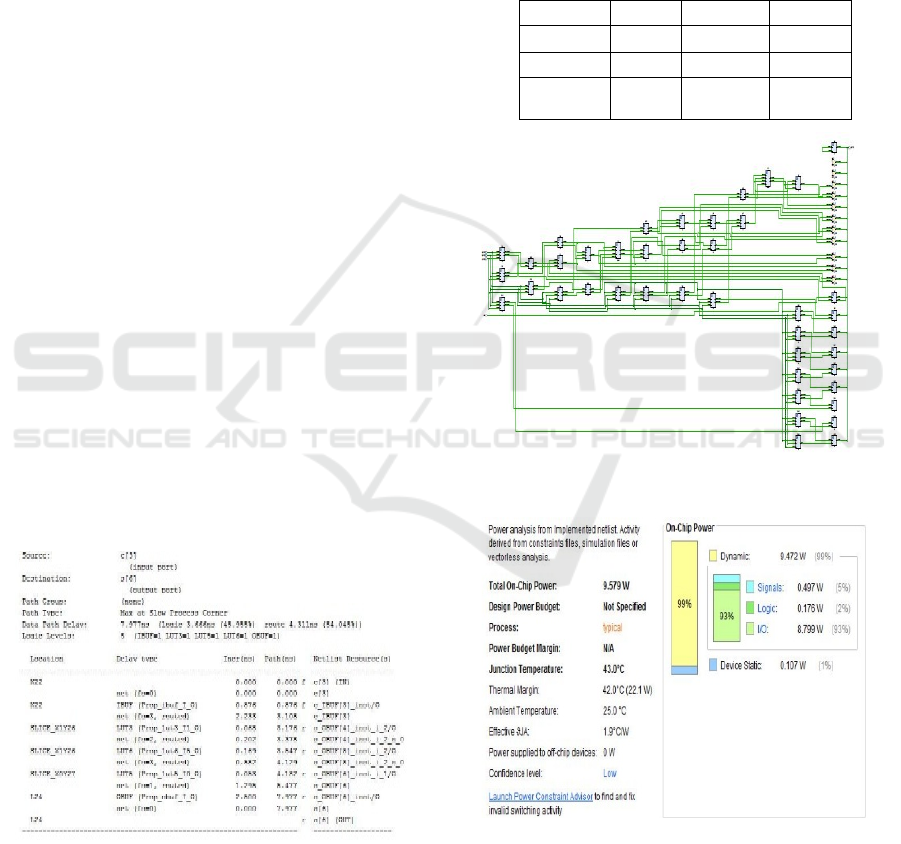
6 RESULT AND DISCUSSION

Figure 4: Delay Report of 16 bits Three operand Binary

Adder.

The TOBA achieves lower power and latency using

a four-stage parallel prefix adder, which minimizes

the fan-in and fan-out. Using an external carry-input

(Cin) is a way to optimize performance by

calculating, generating and propagating signals. The

adder is more efficient in execution, even with a

critical path delay of O (log2n + 1). It results in

faster computation and lower power consumption

than CS3A and HCA adders. This architecture

impacts scalability and speed and is suitable for

pseudorandom number generation and cryptographic

applications.

Table 1: Power, Delay, and Area Analyzis Report.

DESIGN AREA POWER DELAY

CSA 16 14.914W 7.38ns

HCA 24 11.046W 10.15ns

BINARY

ADDER

17 9.579W 7.97ns

Figure 5: RTL Schematic of 16 bit Three operand Binary

Adder.

Figure 6: Power Report of 16 bit Three operand Binary

Added.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

798

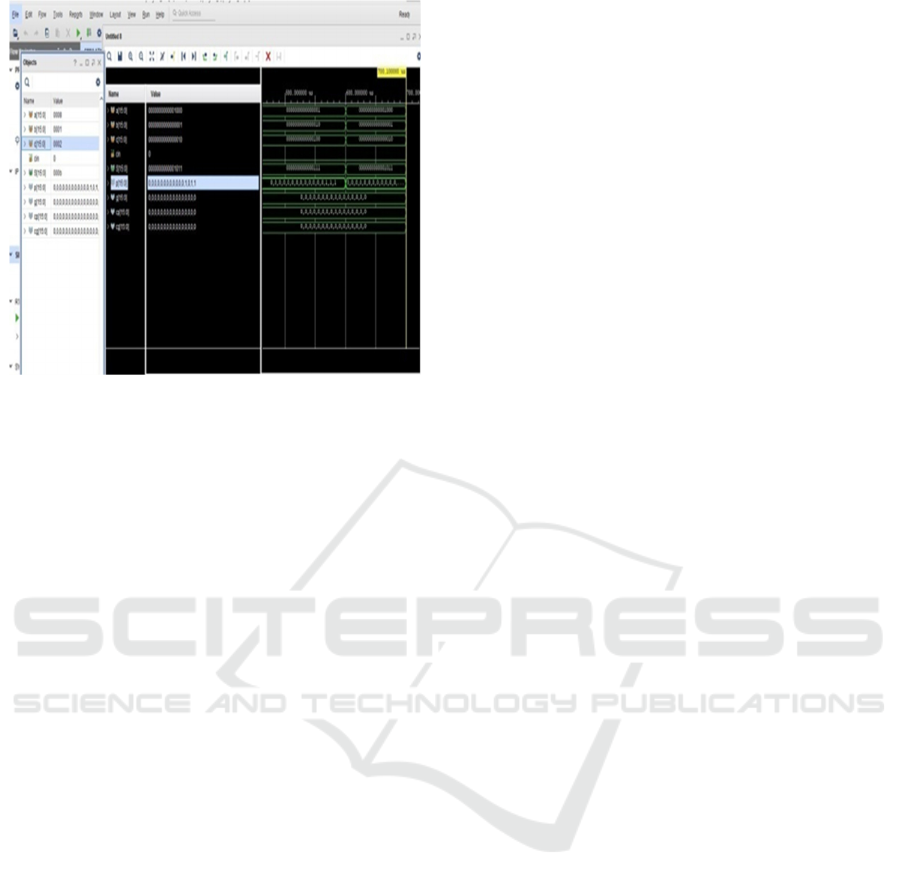
Figure 7: Simulation of 16 bit Three operand Binary

Adder.

7 CONCLUSIONS

Next, the high speed, low power three input (binary)

adder proposed here represents a considerable

progression in the design of digital systems,

especially for use in applications of significance like

RSA Cryptography and Pseudorandom Bit

Generators. The critical path delays of O(log2n) are

achieved by using pre-computed bitwise addition

and carry-prefix computation, outperforming

traditional designs like CS3A and HCA. The

implementation utilizing Vivado 2023.1

corroborated its superiority one more time also it

showed less power dissipation, area usage, Power-

Delay Product (PDP), Area-Delay Product (ADP)

When compared with the CS3A having area of 16,

power of 14.914 W and delay of 7.38 ns and HCA

with area of 24, power of 11.046 W and delay of

10.15 ns, the area, power and delay of proposed

adder were found to be 26, 9.579 W and 7.97 ns

respectively. These features make it well-equipped

for environments that are resource-scarce and need

high-speed, energy-efficient solutions.

REFERENCES

Krishna Vamsi, A., Udaya Kumar, N., BalaSindhuri, K.,

Sai Chandra Teja, G., “A Systematic Delay and Power

Dominant Carry Save Adder Design,” 2018

International Conference on Smart Systems and

Inventive Technology (ICSSIT), 2018.

Nagesh N. Nazare, R. J. Nayana, Pradeep S. Bhat, and

B.S. Premananda, "Design and Analysis of Low-

Power 16-bit Parallel-Prefix Adiabatic Adders," 2018

3rd IEEE International Conference on Recent Trends

in Electronics, Information & Communication

Technology (RTEICT), 2018.

Jafarzadehpour, A. S., Molahosseini, A. S.,

EmraniZarandi, A. A., and Sousa, L., “New Energy-

Efficient Hybrid Wide-Operand Adder Architecture,”

IET Circuits, Devices & Systems, November 2019.

Bagwari, A., and Katna, I., “Low Power Ripple Carry

Adder Using Hybrid 1-Bit Full Adder Circuit,” 2019

11th International Conference on Computational

Intelligence and Communication Networks (CICN),

2019.

Knowles, S., “A Family of Adders,” Proceedings of the

15th IEEE Symposium on Computer Arithmetic

(ARITH), June 2001.

MuthyalaSudhakar, S., Chidambaram, K. P., and

Swartzlander, E. E., “Hybrid Han-Carlson Adder,”

Proceedings of the IEEE 55th International Midwest

Symposium on Circuits and Systems (MWSCAS),

Boise, ID, USA, August 2012.

Bagwari, A., and Katna, I., “Low Power Ripple Carry

Adder Using Hybrid 1-Bit Full Adder Circuit,” 2019

11th International Conference on Computational

Intelligence and Communication Networks (CICN),

2019.

R.P. Brent and H.T. Kung, “A Regular Layout for Parallel

Adders,” IEEE Transactions on Computers, Vol. C-

31, pp. 260-264, 1982.

Ibrahim, A., Gebali, F.: ‘Optimized structures of hybrid

ripple carry and hierarchical carry lookahead adders’,

Microelectron. J., 2015, 46, (9), pp.783–794.

Mohanty, B.K., Patel, S.K.: Area-delay-power efficient

carry select adder IEEE Trans. Circuits Syst.-II:

Express Briefs, 2014, 61, (6), pp. 418–422’.

K. R, S. T, V. N, S. B and S. A, "Design of a Sleep

Transistor and Read, Write Separation based 6T

SRAM Memory Array for Low Power IOT

Applications," 2021 Smart Technologies,

Communication and Robotics (STCR),

Sathyamangalam, India, 2021, pp. 1-5, doi:

10.1109/STCR51658.2021.9588951.

Efﬁcient Three Operand Adder Design with Carry Preﬁx Logic for Reduced Delay

799