Reversible Generative Steganography Leveraging Distribution

Preserving Encoding for Enhanced Data Security and Integrity

J. Uthayakumar

, S. Sreeraj

, C. Sandhiya

, Ram Ganesh G. H.

, T. Mohanraj

and R. Senthilkumar

Department of CSE, Hindusthan Institute of Technology, Coimbatore, Tamil Nadu, India

M.Tech CSE, Sri Krishna College of Engineering and Technology Coimbatore, Tamil Nadu, India

Department of CSE, Nehru Institute of Engineering and Technology Coimbatore, Tamil Nadu, India

Department of IT, Kamaraj College of Engineering and Technology, Virudhunagar, Tamil Nadu, India

Department of CSE, Karpagam Academy of Higher Education, Coimbatore, Tamil Nadu, India

Keywords: Steganography with Reversibility, Model of Generative Action, Coding for Distribution‑Preserving, Data

Inconspicuousness, Recovery of Information without Loss, Protection of Stego‑Images.

Abstract: Distribution-Preserving encoding combined with reversible generative steganography has been a key

development in safe data embedding and retrieval. Achieving lossless recovery is difficult with traditional

stenographic approaches since they frequently compromise reversibility and data integrity. In this paper, a

novel framework that combines a distribution-preserving encoding technique with reversible generative

steganography is proposed. The suggested technique embeds cover images with hidden messages while

guaranteeing that the encoded data maintains its statistical characteristics. In order to ensure imperceptibility

and reversibility, our method uses a deep generative model to map the secret message into a latent space while

maintaining the data distribution. In order to recover the original secret message without distortion, a stego-

image is created and decoded using an inverse generative model. We perform extensive tests on benchmark

datasets to assess the efficacy of our system, proving full reversibility, improved embedding capability, and

security. Our methodology offers state-of-the-art performance, ensuring lossless information retrieval and

preserving high quality in cover images when compared to conventional methods.

1 INTRODUCTION

Since steganography has the ability to secretly inject

messages into digital content, it is crucial for secure

data transmission. Examples of traditional

steganographic techniques that often have limited

capacity, obvious distortions, and are susceptible to

steganalysis include transform-domain embedding

and Least Significant Bit (LSB) substitution.

Furthermore, after message extraction, the original

cover image cannot be totally restored because many

of these approaches are irreversible. Researchers

have looked into reversible steganography as a way

to get around these limitations because it allows for

the full recovery of the cover image and the hidden

message after decoding. The development of

reversible generative steganography, which uses

invertible deep networks like Glow-based models to

learn data distributions and embed secret messages

while preserving statistical properties, has been made

possible by recent advances in deep generative

models, specifically in the area of normalizing flows.

This ensures high security, reversibility, and

imperceptibility. Because distribution-preserving

encoding guarantees that stego-images stay visually

and statistically identical to natural images, detection

becomes much more difficult than with traditional

deep learning-based steganography, which may

introduce residual distortions or require auxiliary data

for extraction. The goal of research in reversible

generative steganography is to create an effective,

high-capacity, and lossless steganographic

framework that addresses important issues like

detectability, reversibility, and robustness.

The necessity for safe and untraceable

information hiding in digital communication is what's

driving this. Many conventional methods fail to

strike a compromise between embedding capacity

and imperceptibility, introduce artifacts that are

observable by contemporary steganalysis techniques,

Uthayakumar, J., Sreeraj, S., Sandhiya, C., H., R. G. G., Mohanraj, T. and Senthilkumar, R.

Reversible Generative Steganography Leveraging Distribution Preserving Encoding for Enhanced Data Security and Integrity.

DOI: 10.5220/0013889000004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 2, pages

723-730

ISBN: 978-989-758-777-1

723

and, following extraction, the original cover image is

not recovered.

Glow-based reversible generative models are the

subject of this study in order to overcome these

difficulties. Probabilistic encoding and decoding

techniques are used to accomplish high-fidelity,

lossless message recovery while maintaining the

cover image's natural distribution. A reversible

encoding-decoding framework that uses Glow-based

normalizing flows, lossless message recovery, a

distribution-preserving mapping technique that

improves security against steganalysis, high-capacity

embedding with imperceptibility, and an optimized

extraction pipeline for effective and reliable message

decoding using inverse generative transformations

are some of the study's main contributions.

Modification-based approaches, which involve

changing transform-domain coefficients or pixel

values to insert hidden information into an existing

cover image, are the mainstay of traditional

steganographic techniques. Ntivuguruzwa and

Ahmad (2023) state that although these techniques

provide a certain degree of protection, they often

create tiny distortions that are detectable by

sophisticated steganalysis tools, particularly at high

hiding capacities. The risk of message disclosure is

increased by these artifacts, which also undermine the

stego-image's imperceptibility. Furthermore, most

traditional steganographic methods are irreversible,

which means that once the hidden message has been

recovered, the original cover image cannot be fully

restored. This restricts their use in delicate

applications like forensic investigations and medical

imaging.

One potential solution to these problems is

generative steganography. (2020) and (2023) assert

that generative models create stego-images, which are

intrinsically secret, rather than altering an existing

cover image. This method improves security by

removing artifacts caused by alteration, which makes

detection much more challenging. Additionally,

generative stego-pictures are quite challenging for

ordinary AIGC detectors to distinguish from other

AI-generated images, despite the fact that methods

for identifying AI-generated content (AIGC) have

been developed to categorize artificial images (2023;

2022).

Current generative steganographic techniques

usually convert secret messages into image labels or

latent noise vectors before supplying them to

generative adversarial networks (GANs).

1.1 Lack of Distribution-Preserving

Encoding

Most GAN-based models encode secret messages in

a way that disrupts the natural statistical distribution

of the generated image. Using statistical analysis in

the feature domain, attackers can identify the

existence of concealed information since the latent

vectors used to create stego-images are different from

those used for regular images (2021; 2021; 2022).

The discriminator's capacity to distinguish stego-

images from regular images is what makes these

techniques secure, although there isn't a solid

theoretical basis for complete security.

1.2 Irreversible Transformations

Perfectly reconstructing the original secret message is

challenging with GAN-based steganography since it

uses a one-way mapping from the latent space to the

image space. Because of this, message extraction is

prone to distortion, particularly when there is more

information packed in the image in high-capacity

circumstances. Because of this irreversibility,

message recovery is less reliable, which makes these

techniques inappropriate for applications that need to

retrieve data without loss.

Glow-based reversible generative steganography

employs advanced encoding and transformation

techniques to ensure secure, lossless information

hiding while maintaining the statistical properties of

cover images. The core algorithm relies on

distribution-preserving mapping, where secret

messages are mapped into a latent space following a

Gaussian distribution rather than being directly

embedded into the image. This ensures that the

encoded message remains indistinguishable from

natural data distributions, significantly enhancing

security against steganalysis. A Glow-based

generative model (a normalizing flow approach) is

utilized to learn an invertible transformation between

image space and latent space, allowing for reversible

image transformation without introducing distortions.

The use of reversible data embedding ensures that

both the message and the original cover image can be

recovered perfectly, overcoming the limitations of

traditional steganographic methods that often

introduce irreversible changes. Entropy encoding

optimizes data compression and embedding

efficiency, maximizing capacity while maintaining

imperceptibility. Furthermore, noise-aware encoding

adjusts the encoding process to account for variations

in image features, enhancing robustness against

detection. By leveraging an inverse mapping

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

724

function, the system ensures that message extraction

is lossless and highly accurate. The combination of

these techniques makes Glow-based generative

steganography a powerful approach for secure,

undetectable, and fully reversible data hiding.

2 RELATED WORKS

Generative Steganography:

As opposed to

traditional modification-based steganography,

which incorporates confidential data into an

existing cover image, generative steganography

generates stego-images from text using generative

models.covert communications. By eliminating

explicit pixel changes, this coverless technique

reduces statistical abnormalities that steganalysis

tools could take advantage of, hence enhancing

security. In order to safeguard digital forensics,

generative steganography has been thoroughly

studied due to its strong anti-detectability. Early

methods of generative steganography used texture

creation to encode secret communications. Data

was incorporated into high-frequency texture

images in (2015), and words were transformed into

fingerprint-like holographic images (2018).

Attackers became suspicious, though, because

these methods created outputs that were visually

odd. Secret communications were encoded using

texture creation in early generative steganographic

techniques. Xu and colleagues (2015) integrated

data into high-frequency texture pictures, (2018)

converted words into holographic visuals that

resembled fingerprints. Attackers became

suspicious, though, because these methods created

outputs that were visually odd. Deep learning-

based generative models were introduced by

academics to increase realism. Techniques based

on GANs., (2014) gained popularity because they

made it possible to create stego-images that looked

realistic. A number of methods embedded secret

messages within significant visual structures using

semantic constraints: GAN-based picture synthesis

was constrained by messages encoded into anime

character attribute labels in (2020) (2017). Since

labels and attributes can only encode a limited

amount of information, these semantic-based

approaches have a low concealing capacity. Later

methods investigated direct message encoding into

GAN noise vectors to boost capacity: . (2018) and.

(2020) created stego-images with directly altered

noise vectors that included secret messages using

Deep Convolutional GANs (DCGANs) (2016). To

create images from message-encoded noise

vectors, (2020) used Wasserstein GAN with

gradient penalty (WGAN-GP) Normalizing flow-

based generative models, which offer invertible

and distribution-preserving transformations

between data and latent spaces, has been

investigated by researchers as a solution to these

problems. In contrast to GANs, normalizing flows

guarantee that each generated image has a

bijective, direct mapping to its associated secret

message, allowing for lossless message extraction.

With the help of normalizing flows like RealNVP

(2017) and Glow (2018), created images can

closely resemble real-world statistical distributions

since they achieve precise likelihood estimate. This

characteristic makes them especially well-suited

for distribution-preserving steganography, which

aims to produce stego-images that, even in feature

space, are identical to real images. Although

studies on normalizing flow-based steganography

are still in their infancy, some notable

developments include Secure picture concealment

and retrieval were made possible by Invertible

picture Encryption (2021), which used normalizing

flows for reversible image changes. The potential

of glow-based models in encoding secret messages

while maintaining picture distribution features was

demonstrated by flow-based steganography

(2022).

Reversible Generative Steganography Security

Definition Theoretically:

The first information-

theoretic security model for steganography was

created in 1998 and measured steganographic

security using relative entropy. The security of

reversible generative steganography with

distribution-preserving encoding is evaluated by

comparing the statistical differences between the

model's stego-images and natural images.

Let X S be a random variable representing the

stego-image space X S with a probability

distribution



(



) P S (X S), and X C be a

random variable representing the natural image

space X C with a probability distribution



(



)

P C (X C). The Jensen-Shannon divergence (JSD)

provides a more symmetric and stable metric for

evaluating the security of reversible generative

steganography than Kullback-Leibler divergence.

























































(1)

where M is the mixed distribution:

 











 





(2)

Reversible Generative Steganography Leveraging Distribution Preserving Encoding for Enhanced Data Security and Integrity

725

In contrast to conventional GAN-based generative

steganography, where non-distribution-preserving

transformations frequently cause the distributions P C

(X C) and P S (X S) to diverge, our Glow-based

normalizing flow model guarantees that the produced

stego-images adhere to the precise statistical

characteristics of natural images. Distribution-

preserving encoding results, which makes messages

harder for steganalyzers to detect while enabling

lossless message recovery via invertible

transformations.

Furthermore, the Wasserstein distance can be used to

measure how similar the two distributions are:















 













 







 



















(3)

where Π (P C, P S) is the set of all conceivable joint

distributions with marginals



P C and



P S.

respectively. Compared to current generative

steganographic techniques, a shorter Wasserstein

distance indicates that the stego-pictures are

indistinguishable from genuine photos,

guaranteeing greater security and imperceptibility.

Reversible Generative Steganography via

Glow-Based Technology with Distribution-

Preserving Encoding:

Among flow-based

generative models that create a bijective mapping

between a simple-distributed latent space and a

complex-distributed image space, in creating

realistic, high-quality images while maintaining an

invertible transformation between the generated

images and the latent vectors, the Glow model

(2018) has proven to be incredibly effective.

Due to these characteristics, Glow-based

models are ideal for distribution-preserving

encoding in reversible generative steganography,

which guarantees lossless message retrieval and

improved security against steganalysis. In this

study, we use the Glow model to create stego-

pictures while maintaining the statistical

consistency between the produced and natural

images.

Latent Space Representation and Distribution-

Preserving Encoding:

With a straightforward,

effective, and computationally viable encoding

strategy, the Glow model uses a Gaussian prior to

approximate the latent space distribution,

efficiently capturing complicated dependencies in

data. Using a straightforward probability

distribution



(



) P Z (Z), which is commonly

represented as a spherical multivariate Gaussian

distribution, In the latent space, let Z be the random

variable. The variable in image space with the

complex probability distribution (



) P X (X) can

also be represented by the letter X.

It is possible to define the probability density

function P Z (Z) as a product of independent

components Z d, given that the dimension of Z is

equal to that of X:











 











(4)

A one-dimensional Gaussian distribution is

represented by (Z d).

A direct transformation between the image space and

latent space is established by training the Glow model

to learn an invertible function () f θ (X) in order to

produce a directive mapping:

  









  









 



 







 (5)

where the encoding and decoding functions are

represented, respectively, by f θ and their inverse, g

θ.

Using a maximum log-likelihood estimation

technique, the Glow model is optimized given a

training dataset P data, which consists of picture

samples X normalized to (0,1)

  

















  













 











 (6)

By using the mapping functions  () f θ (X) and

 () g θ (Z), a pre-trained Glow model can be used

to bijectively translate the image space and latent

space. Thus, a reversible encoding method is enabled,

wherein secret messages are first transformed into

high-quality, realistic stego-images and then mapped

into a Gaussian space that guarantees distribution.

The proposed reversible generative steganographic

technique consists of two primary stages: secret

information extraction and secret information

embedding.

Structure of the Suggested Distribution-

Preserving Encoding Reversible Generative

Steganography: In the secret information

embedding step, a distribution-preserving mapping

technique is used to convert the secret message M into

a Gaussian-distributed latent vector z. Next, a stego-

image I is created using the Glow generative model

 () G θ (z), which guarantees that the secret

information is embedded while preserving a natural

visual look. During secret information extraction, the

receiver can extract the latent vector  ′ z ′ from the

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

726

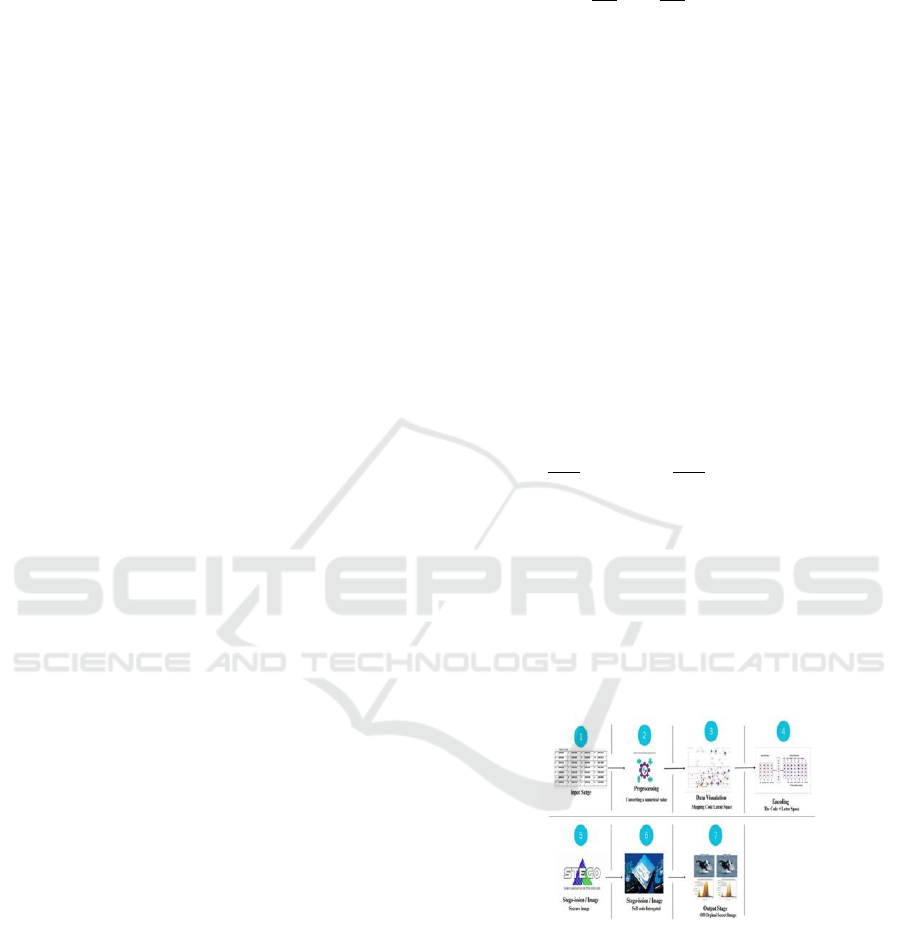
received stego-image  I by using the inverse Glow

function   − 1 ( ) G θ −1(z) since the Glow model

is invertible. The inverse distribution-preserving

mapping is used to recreate the secret message  ′ M

′ from  ′ z ′, allowing for lossless message retrieval

while maintaining security and reversibility.

Embedding Secret Information: The two primary

processes of the secret information embedding stage

are stego-image generation and message mapping.

This is accomplished by first mapping the secret

message to a latent vector using a distribution-

preserving encoding technique. In order to create the

stego-image while preserving statistical consistency

with naturally generated images, the Glow model is

then applied. According to the Glow model (in 2018),

an affine coupling layer, an invertible 1×11 \times

11×1 convolution, and an activation normalization

layer make up each stage of the normalizing flow. In

order to improve security and thwart steganalyzer

detection, the stego-image is made to statistically and

visually mimic real photos. This is done by making

sure that the underlying distribution is preserved

during the message encoding process, which keeps

the resulting stego-images distribution-consistent.

Message Mapping and Image Generation in

Reversible Generative Steganography with

Distribution Preservation Encoding: Since it

enables information to be inserted without a

designated cover image, secret message mapping is

crucial to reversible generative steganography. We

ensure statistical coherence with the original data

distribution by explicitly encoding the secret message

into a latent vector, in contrast to traditional

steganographic techniques. Algorithm 1 describes

how messages are mapped. The first secret message

can be represented by Mori, which is a l-bit bitstream

that must be hidden. The message is initially

encrypted using a secret key sequence k and a

cryptographically secure pseudo-random number

generator (CSPRNG) to increase security.

  



  (7)

In what location is the XOR operator element-wise?

For mapping to be possible, M is split into N equal

segments (m₁, mᵢ, mₙ). M is a multiple of N in length,

which is ensured by using zero padding. The pre-

trained Glow model requires that the encrypted

message M be adjusted to meet the traditional

Gaussian distribution (z  N (0,1)) due to its uniform

distribution (M  U (0,1)). Put z = {z₁, zᵢ, zₙ} as the

latent vector and xᵢ as the decimal representation of

mᵢ. Here is how to make the switch from a uniform to

a Gaussian distribution:





 

























   (8)

where:

The term Rand (a, b) refers to a sampling function that

produces a random value within the range (a, b). The

CDF, or cumulative distribution function, is F (·) for

a Gaussian distribution and F⁻¹ (·) for its inverse.

Thus, the final transformation for creating the latent

vector z is:

A reversible Gaussian-distributed latent space is

mapped into message-embedded values to generate

the latent vector . Start by breaking the secret

message     M into its component components

and converting each one to a decimal value   x i.

The function Rand (, ) Rand(a,b) is used to sample a

uniform distribution and introduce a random

perturbation   y to make sure that these values fall

inside a predetermined range. Values in the range (,)

(a,b) are obtained as a result.

  

















  



















 (9)

By utilizing this distribution-preserving encoding,

the secret message is successfully incorporated

inside the latent space, ensuring that the resulting

stego-images preserve great perceptual and

statistical reliability.

Message Mapping and Image Generation in

Reversible Generative Steganography with

Distribution Preservation Encoding

Figure 1: A Demonstration of the Distribution-Preserving

Encoding Method of Reversible Generative

Steganography.

Mapping messages: Message mapping ensures that

hidden information is incorporated within a latent

vector while retaining a distribution-preserving

transformation in our reversible generative

steganography method. Here's how the mapping

function is defined:

Reversible Generative Steganography Leveraging Distribution Preserving Encoding for Enhanced Data Security and Integrity

727

  













 





 



  























Image generation:

Between the generated stego-

image and the latent space, the Glow model

produces a stable and objective transformation. This

makes reversible information embedding possible,

which enhances the accuracy of the secret message

extraction process after recovery. In summary,

distribution-preserving message mapping boosts

the imperceptibility of hidden information and

improves message extraction accuracy, while the

reversible alteration of the Glow model decreases

the likelihood of steg analysis detection.

3 DISTRIBUTION-

PRESERVING ENCODING

AND REVERSIBLE SECRET

INFORMATION

EXTRACTION IN

GENERATIVE

STEGANOGRAPHY

Reconstructing latent vectors: M = {m₁, ··, mᵢ, ··,

mₙ}, where N is the number of segments of the

encrypted secret message. Unlike conventional

steganographic techniques that modify existing

cover images, our methodology applies a Glow-

based generative model to create entirely new

stego-pictures. Figue 1 show the, a latent vector

with a Gaussian distribution is created from the

encoded secret message after the message mapping

process. Subsequently, this latent vector is

transformed into a corresponding stego-image by

the Glow model, facilitating secret communication.

Secret Message decoding : From z′, the recipient

decodes the message using the known length (l) of

the original secret message Mₒᵣᵢ. Since zero-padding

was used during the embedding process, the

following formula determines how many bits there

are in each segment δ:

 





(11)

  











(12)

Stego-images are statistically indistinguishable: To

avoid identification by attackers, created stego-

pictures must be statistically comparable to images

produced by ordinary generative models with no

information hiding. This is ensured by the mapping

between xi and zi. The conditional probability

distribution is defined as.

  







   











 



(13)

The inverse cumulative distribution function

(CDF) is denoted by F⁻¹(·), while the PDF of a normal

Gaussian distribution is denoted by f(zi). According

to the complete probability theorem, we determine

zi's probability distribution as

Table 1: Superior Accuracy Across Various Hiding Capabilities.

Input:

Secret message:     M ori.

Secret key sequence:  k.

The number of encoding segments is  N.

Pre-trained normalizing flow model:   G θ

Output

Output: Encoded latent representation:  = {

1, …,  

z={z 1,…,z N}

Steps:

To preprocess a message, convert the

characters , , , and  to a binary sequence.

1. Split the binary sequence into N equal-length

segments: {1 , … ,   } {m 1,…,m N}.

2. Map Binary to Latent Space - Convert each

segment (  m i) to a decimal representation

(  x i).

Normalize   x iinside the desired latent

space.

3. Distribution-Preserving Encoding: - Sample

auxiliary noise     (0,1) y i

N(0,1).Encode   x iusing the invertible

sampling function  (  ,   ) S(x i,y i),

ensuring   z ikeeps the original distribution

parameters.

4. Use the Normalizing Flow Model to

transform   z iusing the generative model 

 G θ, creating stego representation   − 1 (

 ) G θ −1(z).

5. Output Encoded Representation: Store the

modified latent vector  for reversible

retrieval.

6. End Algorithm

Accuracy in information extraction in reversible

generative steganography with distribution-

preserving encoding: To evaluate the proposed

method's information extraction accuracy (IEA)

across various hiding capacities, we compare it to

SWE, as shown in Table 1. Superior Accuracy Across

Various Hiding Capabilities The proposed technique

achieves a high IEA (≈1.0) across various hiding

capacities (0.1 to 4.0 bpp). Notably, it outperforms

SWE at various hiding capacities, particularly 0.5,

1.0, 2.0, and 4.0 bpp.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

728

Anti-Detectability Analysis in Reversible

Generative Steganography.: Two well-known

steganalysis models are used in our proposed

reversible generative steganographic technique to

assess its anti-detectability. This technique was first

described in 2012 and uses a set of high-dimensional

handcrafted attributes taken from photographs to

discover hidden information. This popular

steganalyzer examines residuals at the pixel level to

detect statistical irregularities caused by

steganography.

3 CONCLUSIONS

Recent developments in reversible generative

steganography with distribution-preserving encoding

are covered in this paper. These developments

address the shortcomings of conventional

modification-based and irreversible generative

stenographic techniques. The proposed approach

provides bijective transition between generated

stego-images and hidden messages using a Glow-

based normalizing flow model, enabling accurate

message extraction and high concealing capacity.

Unlike traditional steganography approaches, which

produce visible distortions, our method maps the

secret message into a Gaussian-distributed latent

space, resulting in stego-pictures that are statistically

indistinguishable from natural photos. Furthermore,

the Glow model's reversibility enables near-perfect

secret message recovery, even at large hiding

capacities. Furthermore, a comparison with existing

approaches such as SWE, S-UNIWORD, and UT-

6HPF-GAN demonstrates that these methods exhibit

detectability concerns and worse extraction accuracy

at larger embedding rates. Our technique, on the other

hand, retains strong security and resistance against

steganalysis tools like SRM and XuNet, particularly

when hiding capabilities reach 4.0 bpp. Finally, the

suggested distribution-preserving generative

steganographic approach represents a substantial step

forward in secure, reversible, and high-capacity

information concealment. These findings

demonstrate the possibility of normalizing flow-

based models in steganography, paving the path for

future research into more efficient and undetectable

steganographic frameworks.

REFERENCES

Cao, Y., Zhou, Z., Wu, Q., et al. (2020). Coverless

Information Hiding Based on the Generation of Anime

Characters. EURASIP Journal on Image and Video

Processing, 2020(1), 1–15.

Chen, K., Zhou, H., Zhao, H., et al. (2022). Distribution-

Preserving Steganography Based on Text-to-Speech

Generative Models. IEEE Transactions on Dependable

and Secure Computing, 19(5), 3343–3356.

Filler, T., Judas, J., Fridrich, J. J. (2011). Minimizing

Additive Distortion in Steganography Using

Syndrome-Trellis Codes. IEEE Transactions on

Information Forensics and Security, 6(3), 920–935.

Fridrich, J., Kodovsky, J. (2012). Rich Models for

Steganalysis of Digital Images. IEEE Transactions on

Information Forensics and Security, 7(3), 868–882.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., et al. (2014).

Generative Adversarial Nets. In Advances in Neural

Information Processing Systems (NIPS), 2672–2680.

Holub, V., Fridrich, J., Denemark, T. (2014). Universal

Distortion Function for Steganography in an Arbitrary

Domain. EURASIP Journal on Image and Video

Processing, 2014(1), 1–13.

Jiang, W., Hu, D., Yu, C., et al. (2020). A New

Steganography without Embedding Based on

Adversarial Training. In Proceedings of the ACM

Turing Celebration Conference, 219–223.

Karras, T., Aila, T., Laine, S., et al. (2018). Progressive

Growing of GANs for Improved Quality, Stability, and

Variation. In International Conference on Learning

Representations (ICLR).

Kingma, D. P., Dhariwal, P. (2018). Glow: Generative

Flow with Invertible 1 × 1 Convolutions. In Advances

in Neural Information Processing Systems (NIPS),

10215–10224.

Li, J., Niu, K., Liao, L., et al. (2020). A Generative

Steganography Method Based on WGAN–GP. In

International Conference on Artificial Intelligence and

Security, 386–397.

Li, Q., Wang, X., Wang, X., et al. (2021). An Encrypted

Coverless Information Hiding Method Based on

Generative Models. Information Sciences, 553, 19–30.

Liu, M., Zhang, M., Liu, J., et al. (2017). Coverless

Information Hiding Based on Generative Adversarial

Networks. arXiv preprint arXiv:1712.06951.

Liu, X., Ma, Z., Ma, J., et al. (2022). Image

Disentanglement Autoencoder for Steganography

without Embedding. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern

Recognition (CVPR), 2303–2312.

Luo, Y., Qin, J., Xiang, X., et al. (2020). Coverless Image

Steganography Based on Multi-Object Recognition.

IEEE Transactions on Circuits and Systems for Video

Technology, 31(7), 2779–2791.

Luo, Y., Qin, J., Xiang, X., et al. (2020). Coverless Image

Steganography Based on Image Segmentation.

Computers, Materials & Continua, 64(2), 1281–1295.

Pang, K. (2024). FreStega: A Plug-and-Play Method for

Boosting Imperceptibility and Capacity in Generative

Linguistic Steganography for Real-World Scenarios.

arXiv preprint arXiv:2412.19652.

Radford, A., Metz, L., Chintala, S. (2016). Unsupervised

Representation Learning with Deep Convolutional

Reversible Generative Steganography Leveraging Distribution Preserving Encoding for Enhanced Data Security and Integrity

729

Generative Adversarial Networks. In International

Conference on Learning Representations (ICLR).

Tang, W., Zhou, Z., Li, B., et al. (2024). Joint Cost Learning

and Payload Allocation with Image-Wise Attention for

Batch Steganography. IEEE Transactions on

Information Forensics and Security, 19, 2826–2839.

Wu, Y., Wang, J., Zhou, H., et al. (2023). A Resilient and

Accessible Distribution-Preserving Watermark for

Language Models. arXiv preprint arXiv:2310.07710.

Xu, G., Wu, H., Shi, Y. Q. (2016). Structural Design of

Convolutional Neural Networks for Steganalysis. IEEE

Signal Processing Letters, 23(5), 708–712.

Yang, J., Ruan, D., Huang, J., et al. (2019). An Embedding

Cost Learning Framework Using GAN. IEEE

Transactions on Information Forensics and Security,

15, 839–851.

Yu, C., Hu, D., Zheng, S., et al. (2021). An Improved

Steganography without Embedding Based on Attention

GAN. Peer-to-Peer Networking and Applications,

14(3), 1446–1457.

Zhang, Z., Fu, G., Ni, R., et al. (2020). A Generative

Method for Steganography by Cover Synthesis with

Auxiliary Semantics. Tsinghua Science and

Technology, 25(4), 516–527.

Zhu, J., Chen, Z., Yang, L., et al. (2024). Plug-and-Hide:

Provable and Adjustable Diffusion Generative

Steganography. arXiv preprint arXiv:2409.04878.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

730