Enhancing Energy Efficiency and Data Rate in MIMO‑NOMA

Systems Based on Communication Deep Neural Networks for 6G

Communications

R. Poornima, S. Jayachitra, Ajay A., Dhivakar S., Indra Kumar U. and Jayasakthi S P

Department of ECE, K.S.R. College of Engineering, Tiruchengode, Namakkal, Tamil Nadu, India

Keywords: MIMO, Deep Learning, NOMA, Data Rate, Energy Efficiency.

Abstract: The emergence of 6G communication networks requires novel techniques to deliver massive connectivity

with high data rate, and enhanced energy efficiency, driving the future of communication systems. The

integration of Non-Orthogonal Multiple Access (NOMA) with Multiple-Input Multiple-Output (MIMO)

systems, offers a promising solution to enhance system energy efficiency and data rate. Rapidly changing

channel conditions and complex spatial structures degrade system performance and limit its applicability. To

address these restrictions, this article proposes a deep learning-based MIMO-NOMA framework that

maximizes data rate and energy efficiency. Specifically, we develop a novel Communication Deep Neural

Network (CDNN) architecture comprising multiple hidden layers and convolution layers. The deep learning

techniques such as, the CDNN framework uses training algorithms to solve the power allocation problem and

increase MIMO-NOMA's energy efficiency and data rate. Furthermore, simulation results demonstrate that

the suggested CDNN framework has better data rate and energy efficiency than the Secondary BS-aided

scheme, ᾳ- fairness aided based scheme, LSTM-NOMA based scheme and basic deep learning scheme. The

Secondary BS-aided scheme data rate mean is 2.4586, fairness aided based scheme mean is 2.4986, LSTM-

NOMA based scheme mean is 2.5343, deep learning scheme mean is 2.6571 and proposed CDNN scheme

data rate mean is 2.8514. So that proposed CDNN framework has higher energy efficiency and data rate than

compared to other regular methodologies.

1 INTRODUCTION

6G boasts significantly higher data rates, lower

latency, and massive connectivity compared to 5G

and 4G. Key technologies driving these

advancements include MIMO and millimeter-wave

communication, which also enhance capacity,

reliability, and scalability (Andrews et al. 2024).

MIMO employs multiple antennas at base stations to

improve cellular network uplink and downlink

performance. The MIMONOMA system further

boosts efficiency and data rates (Hoydis et al. 2024).

NOMA enables multiple clients to share the same

frequency resources using power domain

multiplexing. Combining NOMA with Orthogonal

Multiple Access (OMA) techniques yields enhanced

spectrum efficiency and high reliability, supporting

massive connectivity and outperforming OFDMA

(Chiu et al. 2025). For millimeter-wave massive

systems, a novel beam space concept for MIMO

minimizes the number of required frequency chains

without compromising performance (Wang et al.

2024). To enhance channel and signal estimation in

orthogonal frequency division multiplexing systems,

deep learning techniques are applied (Ye et al. 2024).

By incorporating Machine Learning (ML) concepts

into the wireless core and edge infrastructure, next-

generation wireless communication systems can

provide IoT devices with ultra-reliable, low-latency

interactions and ubiquitous connectivity, driven by

intelligent, data-driven capabilities (Chen et al. 2025).

600

Poornima, R., Jayachitra, S., A., A., S., D., U., I. K. and S P, J.

Enhancing Energy Efﬁciency and Data Rate in MIMO-NOMA Systems Based on Communication Deep Neural Networks for 6G Communications.

DOI: 10.5220/0013887100004919

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 2, pages

600-607

ISBN: 978-989-758-777-1

2 RELATED WORKS

Over 200 articles in IEEE Xplore and 95 in

academia.edu have been published on MIMO-

NOMA system in past four years. To provide a deep

learning framework and optimize the MIMO-NOMA

system's energy efficiency and data rate after

thorough investigation. To achieve improved power

allocation performance for energy efficiency and data

rate optimization, the initial step is to merge deep

learning with MIMO-NOMA systems (Ding et al.

2024). The capacity gains achievable by MIMO-

NOMA over MIMO-OMA, showing that NOMA can

provide higher spectral efficiency and greater system

capacity than OMA (Zeng et al. 2024). To optimize

and enhance the performance of NOMA systems. By

applying deep learning, the paper aims to improve

key tasks such as signal detection, interference

cancellation, and channel estimation, ultimately

enhancing spectral efficiency and reducing bit error

rates (BER) in NOMA systems (Gui et al. 2024).

Downlink multiuser MIMO systems' NOMA, along

with improvements in beamforming, power

allocation, and user clustering, all of which are crucial

for enhancing system performance. The suggested

CDNN scheme's data rate cluster has a learning rate

of 0.002, 0.001, 0.01, 0.1 (Ali et al.2024). Maximum

data rate and energy efficiency are provided by a deep

learning-based NOMA system with MIMO (Huang et

al. 2024). LSTM based NOMA further develops

aggregate rate, diminishes idleness, and improves

power assignment. The framework accomplishes

total rate: 2.8 Gbps (17% higher than customary

NOMA) Inactivity decrease: 90% and Better

reasonableness for clients with powerless channels

(Huang et al. 2025). It is understood that NOMA is

important the contrast between two channel gains is

exceptionally huge. A crafty lattice precoding

calculation defeats the constraints of customary

NOMA in non-distinct channels by: Adjusting power

assignment in view of channel relationship.

Upgrading the aggregate rate by 13% contrasted with

regular NOMA. Further developing decency by

expanding major areas of strength for the rate (Saito

et al. 2024). The proposed calculation for force and

sub-transporter designation is gotten from the non-

raised power minimization under rate and sub-

transporter reservations, for which an ideal

arrangement is NP-hard. The proposed MIMO-

NOMA accomplishes 35% power productivity

improvement over OMA, 51% better range

productivity, 41% higher total rate than OMA (Tweed

et al. 2025).

From previous findings, it is concluded that

energy efficiency and data rate is increased. The aim

of the study is to further develop the data rate and

energy efficiency between CDNN and deep learning

approaches.

3 METHODOLOGY

Consider a standard downlink MIMO-NOMA system

consisting of a single base station with a uniform,

linear array of M antennas and D multi-antenna users.

Assume Rayleigh fading in the downlink channel.

Each user is equipped with Nr receiving antennas, and

it is assumed that the base station has no knowledge

of each user's individual channel. To adopt NOMA

principles in the MIMO system, users are randomly

grouped into M clusters, each containing N clients

(i.e., D = MN). The transmitted signals at the base

station can be represented by the equation (1)

Y = H s (1)

where H is a M × K precoding matrix, then s is further

formulated in equation (2) as

𝑠 =



𝛽1,1 𝑠1,1 + ⋯ 𝛽1,𝐾𝑠1,𝐾

⋮ ⋱ ⋮

𝛽𝐾,1𝑠𝐾,1 ⋯ 𝛽𝑀,𝐾𝑠𝑀,𝐾







𝑆1⋯

𝑆𝑀

 (2)

Here, sM,K is the information carrying signal that

is received by the N-th client of the M-th cluster,

Where βi,j is a power allocation coefficient of

NOMA.

3.1 MIMO-NOMA System

A deep learning-based MIMO-NOMA system

integrates MIMO-NOMA system with Deep Neural

Network (DNN), leveraging cutting-edge deep

learning techniques to develop a method that

optimizes the sum of energy efficiency and data rate.

To enhance performance, a kernel-based

Communication Deep Neural Network (CDNN) is

designed to approximate the MIMO-NOMA system's

power allocation optimization problem. The base

station implements the trained CDNN, which assigns

a distinct power to each user. The characteristics of

the channel links and clients are used as input

features, without physically modeling the users in the

CDNN architecture. As a result, the training examples

incorporate information about client and channel

conditions, improving efficiency.

A proposed CDNN framework is used to estimate

the system, using different convolutional and well-

Enhancing Energy Efﬁciency and Data Rate in MIMO-NOMA Systems Based on Communication Deep Neural Networks for 6G

Communications

601

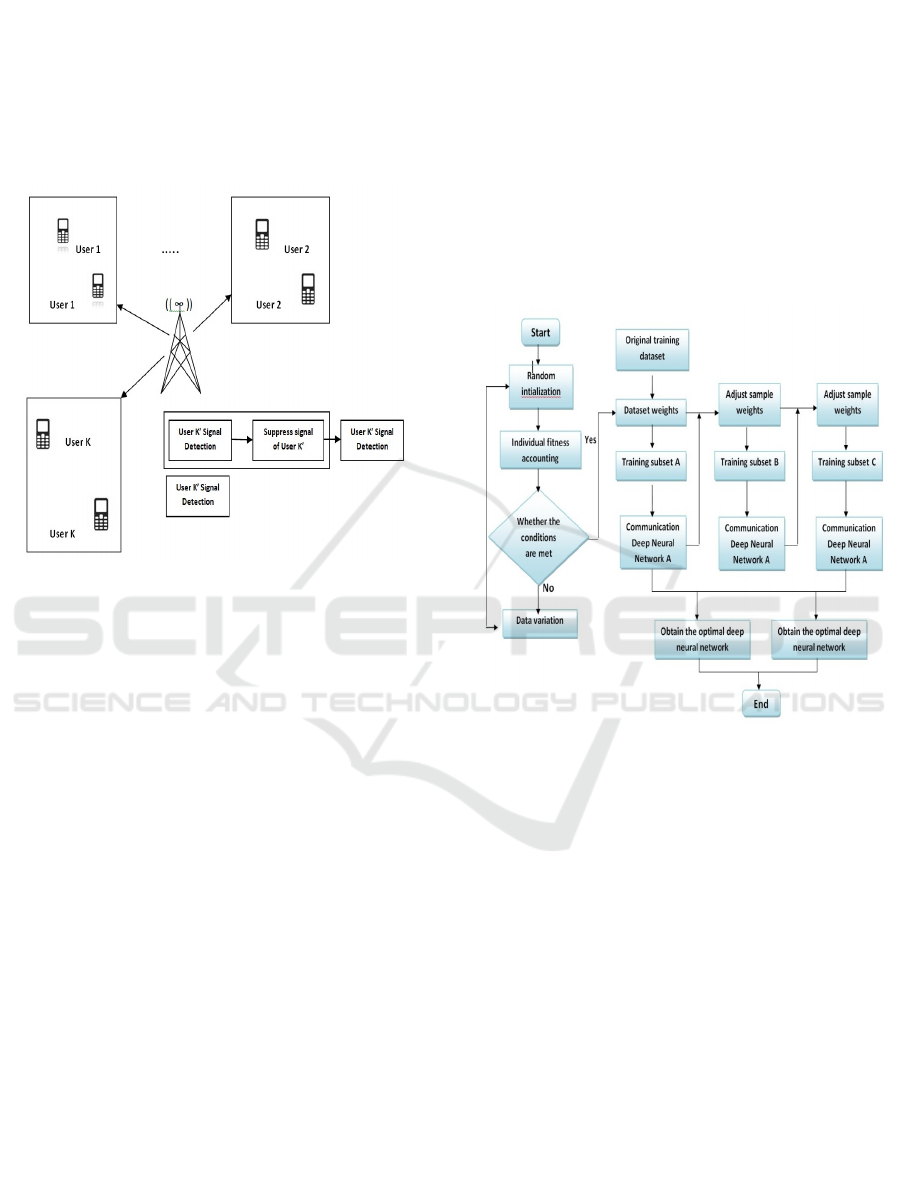
designed hidden layers (Fig.1.) that use certain

activation functions to compute. Moreover, from the

proposed CDNN structure, a new power distribution

strategy is presented for enhancing the energy

efficiency and data rate performance. The technique

can improve energy efficiency and data rate. Figure 1

shows the Multiple clusters of MIMO-NOMA

system.

Figure 1: Multiple Clusters of MIMO-NOMA System.

3.2 MIMO-NOMA System with Deep

Learning

The goal is to optimize the data rate and energy

efficiency of the MIMO-NOMA system. The data

rate of the N-th user in the first cluster is obtained in

this equation (3) and is represented by

𝐾1,𝑀= log



(1 +𝛾𝑁1,𝑀) (3)

The Figure 2 represents the workflow for

optimizing deep neural networks involves a multi-

step process data sampling, training subsets, and

fitness evaluation.

The process begins with the initialization step,

where random values are assigned to represent the

starting conditions of the algorithm. The fitness or

effectiveness of the current configuration is evaluated

based on specific criteria, such as model accuracy or

other performance metrics. A decision is made based

on whether predefined conditions are met. If these

conditions are not met, the system proceeds the data

for variation step, where adjustments are made to the

dataset or sampling method to improve performance.

If the conditions are met, the system progresses to the

next step.

The process starts with the original database,

which serves as the basis for creating subsets and

adjusting weights. The weights of the dataset are

adjusted to emphasize or de-emphasize specific

samples, allowing for better training of models on

critical data points. The dataset is split into multiple

subsets (e.g., A, B, C) with adjusted sample weights

to ensure diverse training. Each subset is used to train

separate deep neural networks. It evaluates each

trained network and identifies the optimal one based

on predefined criteria, such as accuracy, loss, or

generalization performance.

Figure 2: Flowchart of Deep Neural Network Optimization.

3.3 CDNN Based MIMO-NOMA

System Architecture

This framework (Figure 3) comprises 11

convolutional layers and a max-pooling layer along

with fully connected layers, the architecture is

denoted as (Conv, FC, MaxPool, S), where the

architecture comprises convolutional layers (Conv),

fully connected layers (FC), and max-pooling

operations (MaxPool) with specified strides (S).

Furthermore, the precoding matrix P is composed of

individual precoders for each antenna. The output

precoder, denoted as p

m, along with its associated

power allocation factors, produces the optimal power

allocation results.

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

602

Figure 3: CDNN Based Deep Learning for Mimo- Noma

System.

4 SIMULATION RESULTS AND

ANALYSIS

The simulation was based on improving energy

efficiency and data rate using the communication

deep neural network method, and using

Communication toolbox includes simulink blocks in

MATLAB to plot the efficiency and data rate. The

Sample data was established based on previous study

results (Huang, Yang, et al., n.d.).

4.1 Comparison Data Rate with SNR

Figure 4: A Comparative Analysis of the Data Rate

Performances Is Presented, Evaluating the Proposed CDNN

Scheme Against Existing Approaches, Including the

LSTM-NOMA Based Scheme, Α-Fairness Based Scheme,

and Secondary Bs-Aided Scheme.

The Figure 4, compares data rate performances of

different approaches next to SNR (dB). The proposed

CDNN-based approach achieves the highest data rate,

followed by the deep learning approach and NOMA-

based LSTM scheme. The α-fairness based scheme

performs moderately, while the Secondary BS-aided

scheme has the lowest data rate.

4.2 Comparison Data Rate per Cluster

with SNR

Figure 5: Comparative Analysis of the Data Rate Per

Cluster with Different Learning Rates.

The Figure 5, Illustrates the data rate/cluster for

the future CDNN scheme with different learning rates

(LR). As SNR increases, the data rate also improves

for all learning rates. A lower learning rate (LR =

0.002) achieves the highest data rate, while a higher

learning rate (LR = 0.1) results in the lowest

performance. This suggests that smaller learning rates

enhance the model's efficiency in optimizing data

rate.

4.3 Comparison of BER with Signal to

Noise Ratio (SNR)

Figure 6: A Comparative Analysis of BER for Different

Snr.

The Figure 6 compares the data rate performance

of different approaches against SNR (dB) in terms of

bit-error rate (eps/Hz). The proposed CDNN-based

approach shows the lowest bit-error rate, indicating

superior performance. Other methods, such as deep

learning, LSTM-NOMA, αfairness, and Secondary

BS-aided schemes, have higher error rates. This

Enhancing Energy Efﬁciency and Data Rate in MIMO-NOMA Systems Based on Communication Deep Neural Networks for 6G

Communications

603

suggests that CDNN-based optimization is more

efficient in improving data rate performance.

4.4 Comparison Energy Efficiency with

SNR

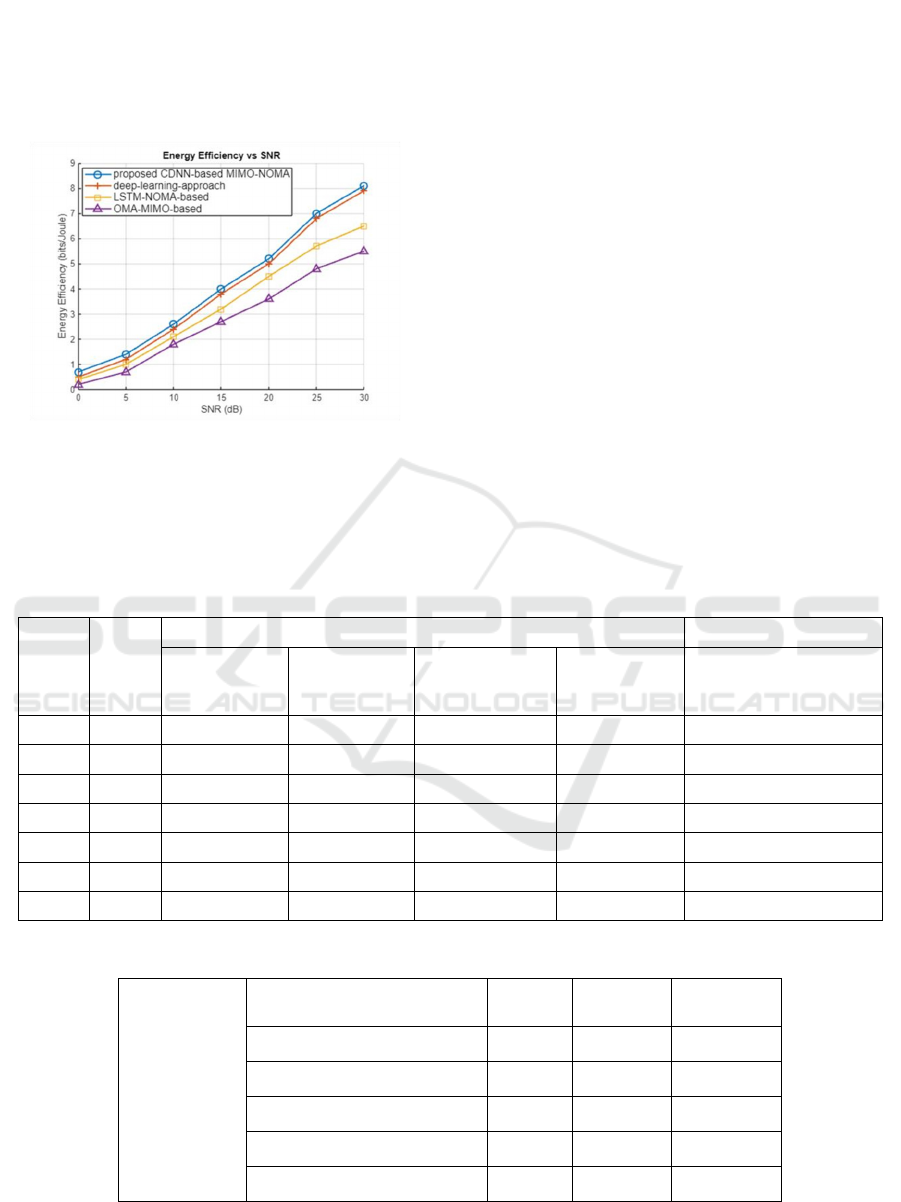
Figure 7: A Comparison of Energy Efficiency Versus

Signal-To-Noise Ratio (SNR) Is Presented for the Proposed

CDNN-Based MIMO-NOMA Scheme, the LSTM-NOMA

Based Scheme, and the Conventional OMA-MIMO Based

Scheme.

The Figure 7 compares energy efficiency

(bits/Joule) versus SNR (dB) for different

approaches. The proposed method (blue line)

achieves the highest energy efficiency, followed

closely by the deep-learning approach. NOMA based

LSTM and MIMO-based OMA methods perform

worse, with OMA-MIMO being the least efficient.

This indicates that CDNN-based optimization

enhances energy efficiency in wireless

communication.

5 STATISTICAL ANALYSIS

Data obtained from parameters such as SNR (dB) for

secondary BS-aided scheme, fairness-based scheme,

LSTM-NOMA based scheme, deep learning scheme,

and proposed CDNN scheme are analyzed using

SPSS version 26.0 in Table 1. SPSS software is used

to calculate the group statistics and the independent

samples (Gui et al., n.d.). Independent variables for

the study are the number of Schemes while SNR

(dB)are dependent variables.

Table 1: Date Rate for Different Schemes.

SNR

(dB)

Data Rate (Bits/Hertz)

Secondary BS

aided scheme

ᾳ-

fairness based

scheme

LSTM-

NOMA based

scheme

Deep learning

approach

Proposed

CDNN-based approach

1 0 0.4 1.6 1.8 2.1 2.3

2 5 1.2 2.5 2.9 3.4 3.9

3 10 2.6 3.9 4.5 5 5.5

4 15 3.9 5.5 6.2 6.8 7.3

5 20 5.5 7.3 8 8.9 9.6

6 25 7.1 9 10.5 11.3 12.1

7 30 8.7 10.8 12 13.8 14.5

Table 2: T-Test Comparison Means Data Rate Improvement of Proposed CDNN Scheme Approaches Other Schemes.

Data

rate

Scheme Mean

Std.

Dev

Std. Error of

Mean

Secondary BS-aided scheme 2.4586 0.32526 1.3433

ᾳ-fairness based scheme 2.4986 0.35569 1.3444

LSTM-NOMA based scheme 2.5343 0.38883 1.4696

Deep learning approach 2.6571 0.41097 1.5533

Proposed CDNN based scheme 2.8514 0.45481 1.7190

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

604

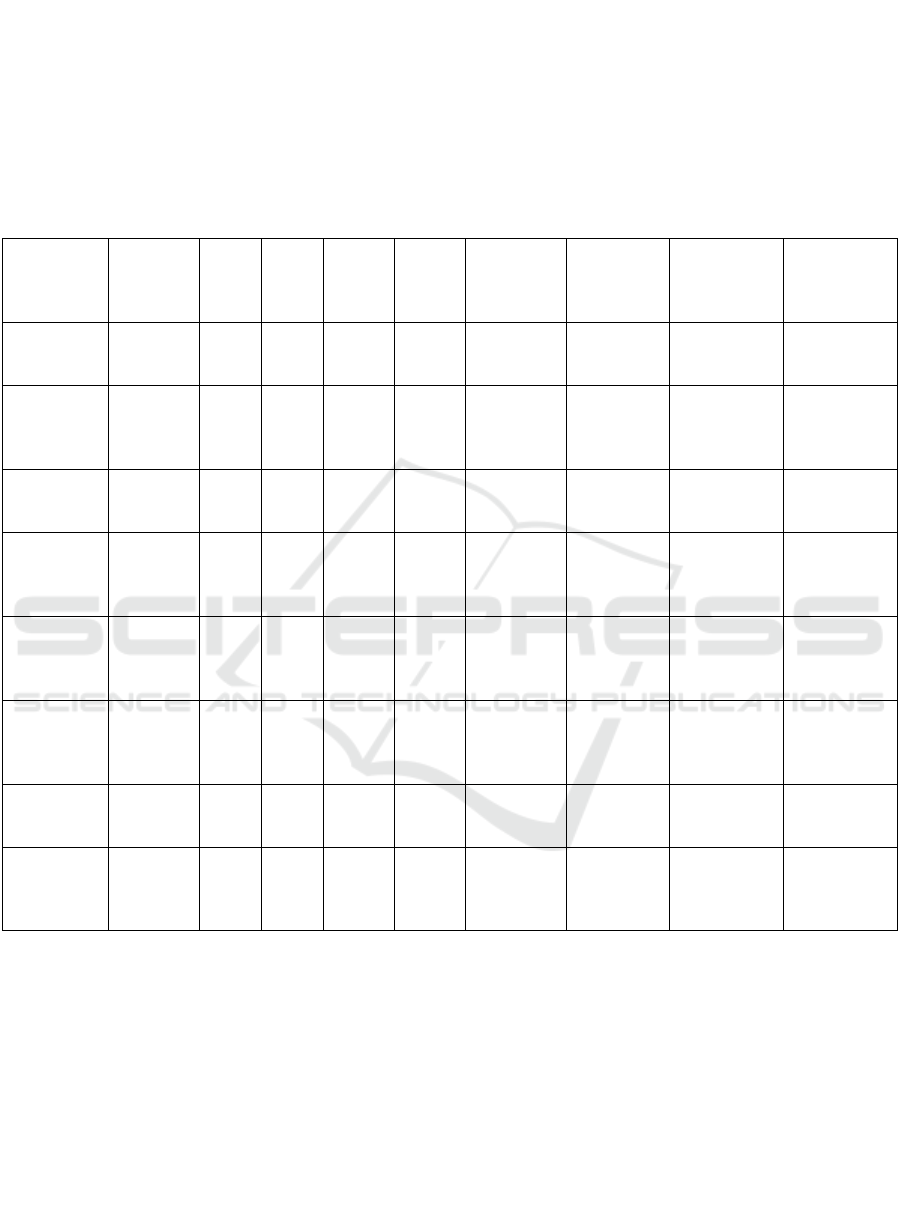
In Proposed CDNN based scheme the N is 7 and

mean value is 2.8514 and Std. deviation is 0.45481

and the Std.error mean is 1. 7190.It shows that

proposed CDNN has high data rate compared to

another scheme. Table 2 shows the T-Test

comparison means data rate improvement of

proposed CDNN scheme approaches other schemes.

Table 3 shows the Independent samples test. T-Test

comparison of, secondary BS-aided scheme, LSTM-

NOMA based

scheme, the fairness-based scheme and deep learning

with proposed CDNN based scheme. (p<0.05).

Table 3: Independent samples test. T-Test comparison of, secondary BS-aided scheme, LSTM-NOMA based scheme, the

fairness-based scheme and deep learning with proposed CDNN based scheme. (p<0.05).

Scheme Levene’s

Test F

Sig t df Sig

(2-

tailed)

Mean

Difference

Std. Error

Difference

95%

Confidence

Interval

(Lower)

95%

Confidence

Interval

(Upper)

Fairness

based

scheme

0.313 0.586 -

1.617

12 0.032 -0.35286 0.21823 -0.82833 0.12262

Equal

variances

not

assume

1.617

11.341 0.033 -0.35286 0.83141 -0.83141 0.12570

Secondary

based

scheme

0.014 0.907 -

1.287

12 0.022 -0.30286 0.23534 -0.81562 0.20991

Equal

variances

not

assume

1.287

11.946 0.023 -0.30286 0.23534 -0.81588 0.21016

LSTM-

NOMA

based

scheme

0.059 0.812 -

1.369

12 0.019 -0.31714 0.23168 -0.82194 0.18765

Equal

variances

not

assume

1.369

11.879 0.019 -0.31714 0.23168 -0.82251 0.18823

Deep

learning

rate

0.114 0.741 -

0.859

12 0.047 -0.19429 0.22616 -0.68705 0.29847

Equal

variances

not

assume

0.859

11.717 0.048 -0.19429 0.22616 -0.68837 0.29980

6 DISCUSSION

The proposed CDNN based scheme has better energy

efficiency and data rate than the Secondary BS-aided

scheme, fairness aided based scheme, NOMA based

LSTM scheme, deep learning-based scheme. The

corresponding changes in Std.error mean from 1.3433

to 1. 7190.The result obtained in the research are

having a high data rate compared to previous studies.

In cellular networks, MIMO technology employs

multiple antennas at the base station to enhance

communication in both the uplink and downlink

directions. The method increases the energy

efficiency and enhanced spectral (Hoydis, ten Brink,

and Debbah, n.d.). Through power domain

multiplexing, the non-orthogonal multiple access

enables several clients to share the similar frequency

resources. (Saito et al., n.d.). That 6G won't be a

straightforward examination of more reach at high-

Enhancing Energy Efﬁciency and Data Rate in MIMO-NOMA Systems Based on Communication Deep Neural Networks for 6G

Communications

605

repeat gatherings, but it will rather be a mix of

impending creative examples driven by empowering,

essential organizations.6G will coordinate quantum

technologies, and blockchain to make a secure,

insightful, and sustainable worldwide organization

(Saad et al. 2025).

By applying deep learning, the paper aims to

improve key tasks such as signal detection,

interference cancellation, and channel estimation,

ultimately enhancing spectral efficiency and reducing

bit error rates (BER) in NOMA systems (Gui et al.,

n.d.). Data rate per cluster of the proposed scheme for

the learning rate is set as 0.002, 0.001, 0.01, 0.1 (Ali,

Hossain,and Kim, n.d.).The calculation meets from

any beginning stage, and it arrives at inside 1/2 rates

per client for each result aspect from the aggregate

limit after only one cycle. Sum Limit Estimation:

Scopes inside 0.5 rates/client/yield aspect after one

iteration. Convergence Rate: The calculation

accomplishes 95% of the ideal limit inside 5 emphasis

(Yu et al. 2025). Remote frameworks where the hubs

work on batteries with the goal that energy utilization

should be limited while fulfilling given throughput

and postpone prerequisites are thought of. In this

unique situation, the best regulation methodology to

limit the complete energy utilization expected to send

a given number of pieces is broken down (Cui et al.

2025).

7 CONCLUSIONS

To enhance energy efficiency and data rate of the

MIMO- NOMA system using a communication deep

neural network was designed. The proposed CDNN

based scheme is better than the Secondary BS-aided

scheme, fairness aided based scheme, NOMA based

LSTM scheme, deep learning scheme. In Secondary

BS-aided based scheme the data rate mean is 2.4586,

fairness aided based scheme mean is 2.4986, LSTM-

NOMA based scheme mean is 2.5343, deep learning

scheme mean is 2.6571 and proposed CDNN scheme

mean is 2.8514. For the secondary BS-aided scheme,

the standard deviation is 0.32526; for the fairness-

based scheme, it is 0.35569; for the LSTM-NOMA, it

is 0.41097; for the deep learning approach, it is

0.41097; and for the proposed CDNN scheme, it

represents 0.45481.

8 SCOPE FOR FUTURE WORKS

In future, our focus will be directed towards

thoroughly analyzing and addressing security

challenges to safeguard the system against potential

threats. At the same time, we will work on enhancing

system capacity to improve performance, scalability,

and overall efficiency, ensuring that it meets current

and future demands effectively.

REFERENCES

Ali, Shipon, Ekram Hossain, and Dong in Kim. n.d. “Non-

Orthogonal Multiple Access (NOMA) for Downlink

Multiuser MIMO Systems: User Clustering,

Beamforming, and Power Allocation.” Accessed

December 25, 2024. https://ieeexplore.ieee.org/abstrac

t/document/7802615.

Andrews, Jeffrey G., Stefano Buzzi, Wan Choi, Stephen V.

Hanly, Angel Lozano, Anthony C. K. Soong,and

Jianzhong Charlie Zhang. n.d. “What Will 5G Be?”

Accessed, December 24,2024.https://ieeexplore.ieee.or

g/abstract/document/6824752/.

Chen, Mingzhe, Ursula Challita, Walid Saad,Changchuan

Yin, and Mérouane Debbah. n.d. “Artificial Neural

Networks-Based Machine Learning for Wireless

Networks: A Tutorial.” Accessed February 1, 2025.

https://ieeexplore.ieee.org/abstract/document/8755300.

Chiu, Hsiao-Ting, and Rung-Hung Gau.n.d. “Opportunistic

Matrix Precoding for Non-Separable Wireless MIMO-

NOMA Networks.” Accessed February 1, 2025.

https://ieeexplore.ieee.org/abstract/document/8417599.

Cui, Shuguang, A. J. Goldsmith, and A. Bahai. n.d.

“Energy-Constrained Modulation Optimization.”

Accessed February1,2025. https://ieeexplore.ieee.org/a

bstract/document/1532220.

Ding, Zhiguo, Fumiyuki Adachi, and H. Vincent Poor.n.d.

“The Application of MIMO to Non-Orthogonal

Multiple Access.” Accessed December 25,

2024.https://ieeexplore.ieee.org/abstract/document/723

6924/.

Gui, Guan, Hongji Huang, Yiwei Song, and Hikmet Sari.

n.d. “Deep Learning for an Effective Non- Orthogonal

Multiple Access Scheme.” Accessed December 25,

2024.

https://ieeexplore.ieee.org/abstract/document/8387468.

Hoydis, Jakob, Stephan ten Brink, and Merouane Debbah.

n.d. “Massive MIMO in the UL/DL of Cellular

Networks: How Many Antennas Do We Need?”

Accessed December-24,2024.

https://ieeexplore.ieee.org/abstract/document/6415388.

Huang, Hongji, Yuchun Yang, Zhiguo Ding, Hong Wang,

Hikmet Sari, and Fumiyuki Adachi. n.d.“Deep

Learning-Based Sum Data Rate and Energy Efficiency

Optimization for MIMO-NOMA Systems.” Accessed

ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,

COMMUNICATION, AND COMPUTING TECHNOLOGIES

606

December-25,2024.

https://ieeexplore.ieee.org/abstract/document/9093213.

Huang, Hongji, Yiwei Song, Jie Yang, Guan Gui, and

Fumiyuki Adachi. n.d. “Deep Learning Based Millime

ter Wave Massive MIMO for Hybrid Precoding.” Acc

essed February-1,2025.

https://ieeexplore.ieee.org/abstract/document/8618345.

R. Poornima and A. Mahabub Basha, “Efficient Detection

of Signal in MIMO System Using Modified Memetic

Algorithm with Higher Order QAM Constellations”

Appl. Math. Inf. Sci. 12, No. 3, 665-671 (2018).

Saad, Walid, Mehdi Bennis, and Mingzhe Chen. n.d. “A

Vision of 6G Wireless Systems: Applications, Trends,

Technologies, and Open Research Problems.”

Accessed February 1,2025.https://ieeexplore.ieee.org/a

bstract/document/8869705.

Saito, Yuya, Anass Benjebbour, Yoshihisa Kishiyama, and

Takehiro Nakamura. n.d. “System-Level Performance

Evaluation of Downlink Non-Orthogonal Multiple

Access (NOMA).” AccessedDecember-24,2024,

https://ieeexplore.ieee.org/abstract/document/6666209.

Tapas Bapu B.R., S. Sivakumar, R. Subhashini and

R.Poornima “Evolutionary gravitational Neocognitron

neural network based differential spatial modulation

detection scheme for uplink multiple user huge MIMO

systems”Dec-2022,(258),

https://doi.org/10.1016/j.knosys.2022.109993.

Tweed, Daniel, and Tho Le-Ngoc. n.d. “Dynamic Resource

Allocation for Uplink MIMO NOMA VWN with

Imperfect SIC.” Accessed February 1,

2025.https://ieeexplore.ieee.org/abstract/document/842

2363.

Wang, Bichai, Linglong Dai, Zhaocheng Wang, Ning Ge,

and Shidong Zhou. n.d. “Spectrum and Energy-

Efficient Beamspace MIMO-NOMA for Millimeter-

Wave Communications Using Lens Antenna Array.”

Accessed December 24,2024.https://ieeexplore.ieee.or

g/abstract/document/7974749/.

Ye, Hao, Geoffrey Ye Li, and Biing-Hwang Juang. n.d.

“Power of Deep Learning for Channel Estimation and

Signal Detection in OFDM Systems.” Accessed

December 24, 2024.https://ieeexplore.ieee.org/abstract

/document/8052521.

Yu, Wei, Wonjong Rhee, S. Boyd, and J. M. Cioffi. n.d.

“Iterative Water-Filling for Gaussian Vector

MultipleAccess Channels.” Accessed February 1, 2025.

https://ieeexplore.ieee.org/abstract/document/1262622.

Zeng, Ming, Animesh Yadav, Octavia A. Dobre, Georgios

I. Tsiropoulos, and H. Vincent Poor. n.d. “Capacity

Comparison Between MIMO-NOMA andMIMO-

OMA with Multiple Users in a Cluster.” Accessed

December25,2024.https://ieeexplore.ieee.org/abstract/

document/7974731.

Enhancing Energy Efﬁciency and Data Rate in MIMO-NOMA Systems Based on Communication Deep Neural Networks for 6G

Communications

607