
Pythagorean Neutrosophic Fuzzy Soft Graph
R. Deepa
1
, S. Tharani
1
, T. Kavitha
1
, N. Sarala
2
and B. Ithayapriya
1
1
Department of Mathematics, E.G.S. Pillay Engineering College, Nagapattinam, Tamil Nadu, India
2
Head of Department of Mathematics, A.D.M. College, Nagapattinam, Tamil Nadu, India
Keywords: Fuzzy Soft Graph, Pythagorean Neutrosophic Fuzzy Graphs, Pythagorean Neutrosophic Set.
Abstract: This paper contains about Pythagorean neutrosophic fuzzy soft graphs (PNFSG).Let us consider neutosophic
set and neutrosophic components and Pythagorean fuzzy set with condition 0≤ (x)2 + B(x)2 + (x)2
≤1.Through this paper we can get idea to apply Pythagorean neutrosophic set to fuzzy soft graphs and can
know some kind on PNFSG with examples.
1 INTRODUCTION
Fuzzy graphs are useful to represent relationships
which deal with uncertainty and it differs greatly from
classical graphs. It has numerous applications to
problems in computer science, electrical engineering,
system analysis, operation research, economics,
networking routing, transportation, etc. interval-
valued Fuzzy Graphs are defined by Akram and
Dudec.
Atanassov introduced the concept of intuitionistic
fuzzy relations and intuitionistic Fuzzy Graph. In fact
interval-valued fuzzy graphs and intuitionistic fuzzy
graphs are two different models that extend theory of
fuzzy graph. S.N.Mishra and A.Pal introduces the
product of interval values intuitionistic fuzzy graph.
Degree of Components of fuzzy set in neutrosophic
set was introduced by smarandache. Let us consider
three cases which is indeterminacy, truth and falsity
with 0
(x)
2
+
B
(x)
2
+
(x)
2
1as Pythagorean
neutrosophic set. From this paper we can apply
Pythagorean neutrosophic set to fuzzy soft graphs
2 PYTHAGOREAN FUZZY SET
(PFS)
Pythagorean fuzzy set (PFS) set of U is P = {< q,
(q),
(q)>:q
N where
(q) and
(q) from N to
[0,1]
represents degree of membership and non-
membership of q in P correspondingly for all q
N
the following Condition should be satisfied 0
+
(q)
1
2.1 Pythagorean Fuzzy Graph (PFG)
A Pythagorean fuzzy graph (PFG) is G = (V, E) with
and
from N to [0,1] be a membership, non-
membership function of N and 0
+
(q)
1
for all q
N such that
(ab)
(a)
(b)
(ab)
(a)
(b)
Where
,
from NxN to [0,1] be a membership,
non-membership function of E and 0
+
(ab) 1 for all ab
E
3 PYTHAGOREAN
NEUTROSOPHIC FUZZY SOFT
GRAPHS
Definition 3.1: Fuzzy Soft Graph
The FSG is defined by 4 tuple as = (
,
1
,
2
, )
such that
•
=
(
,
)
is a simple graph,
•
is a nonempty set of attributes,
•
(
1
,
)
is a FSS over ,
•
(
2
, ) is a FSS over ,
1.
(
1
(
)
,
2
(
)
)
is
a
fuzzy
soft
graph
of
, .
That is,
2
(
)
≤
{
1
(
)(
1
)
,
1
(
)(
2
)}
, and
1
,
2
. Note that
2
(
)(
1
2
)
= 0,
1
2
× − and .
316
Deepa, R., Tharani, S., Kavitha, T., Sarala, N. and Ithayapriya, B.
Pythagorean Neutrosophic Fuzzy Soft Graph.
DOI: 10.5220/0013882200004919
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Research and Development in Information, Communication, and Computing Technologies (ICRDICCT‘25 2025) - Volume 2, pages
316-320
ISBN: 978-989-758-777-1
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
The fuzzy soft graph (
1
(
)
,
2
(
)
) is defined by
(
)
for simplicity.
Definition 3.2:
An Intuitionistic fuzzy soft graph
˜
= (G*,
˜
,
,
˜
,
,
A) is
such that
(i)
G* = (V, E) is a simple graph.
(ii)
A is a nonempty set of parameters
(iii)
(
˜
,
, A) is a intuitionistic fuzzy soft set over V.
(iv)
(
˜
,
,
A) is a intuitionistic fuzzy soft set over E.
(v)
(
˜
,
,
˜
,
)
is a intuitionistic fuzzy soft graph
of G* for all a A is
˜
(a) (xy) ≤ min {
˜
,
(a) (x),
˜
(a) (y)} and
˜
(a) (xy) ≤ max {
˜
(a) (x),
˜
(a) (y)} for all
a
A, x, y
V. The intuitionistic fuzzy soft graph
(
˜
,
(a),
˜
,
(a)) is denoted by
˜
β , δ
(a).
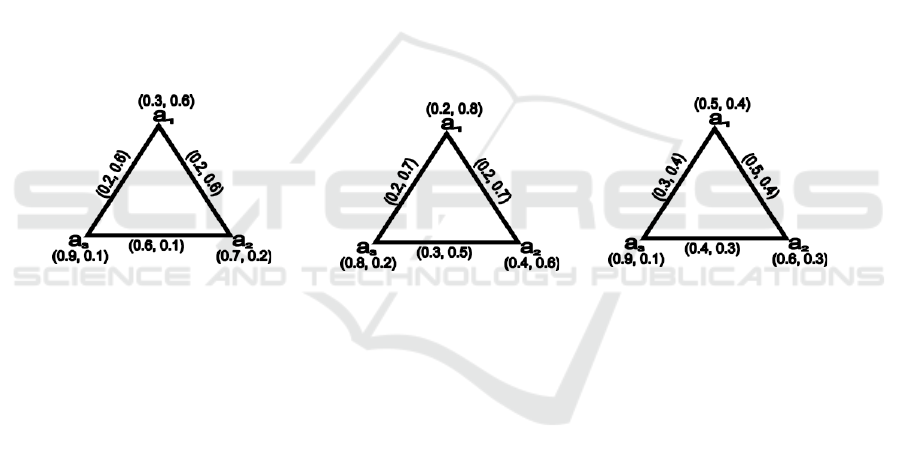
Example 3.2: Consider a simple graph G* = (V,
E) such that V = {a
1
, a
2
, a
3
} and E = {a
1
a
2
, a
2
a
3
,
a
1
a
3
} Let A = {e
1
, e
2
, e
3
} be a parameter set and (
˜
,
,
A) be a intuitionistic fuzzy soft set over V with
intuitionistic fuzzy approximate function
˜
,
: A
→ IF
V
Consider,
˜
,
(e
1
) = {a
1
/(0.3, 0.6), a
2
/(0.7, 0.2), a
3
/(0.9, 0.1)}
˜
,
(e
2
) = {a
1
/(0.2, 0.8), a
2
/(0.4, 0.6), a
3
/(0.8, 0.2)}
˜
,
(e
3
) = {a
1
/(0.5, 0.4), a
2
/(0.6, 0.3), a
3
/(0.9, 0.1)}
Let
(
˜
,
,
A) be a intuitionistic fuzzy soft set over E
with
˜
,
(e
1
) = {a
1
a
2
/(0.2, 0.6), a
2
a
3
/(0.6, 0.1), a
1
a
3
/(0.2,
0.6)}
˜
,
(e
2
) = {a
1
a
2
/(0.2, 0.7), a
2
a
3
/(0.3, 0.5), a
1
a
3
/(0.2,
0.7)}
˜
,
(e
3
) = {a
1
a
2
/(0.5, 0.4), a
2
a
3
/(0.4, 0.3), a
1
a
3
/(0.3,
0.4)}
Thus
˜
,
(e
1
)
= (
˜
,
(e
1
),
˜
,
(e
1
))(Figure 2)
˜
,
(e
2
)
= (
˜
,
(e
2
),
˜
,
(e
2
))
(Figure 3)
˜
,
(e
3
)
= (
˜
,
(e
3
),
˜
,
(e
3
)) is an (Figure 4)
intuitionistic fuzzy soft subgraph and
˜
=
(G*,
˜
,
,
˜
,
,
A) is
a
intuitionistic fuzzy
soft
graph.
Definition 3.3:
Pythagorean Neutrosophic Fuzzy
Soft Graphs
Pythagorean Neutrosophic Fuzzy soft
Graph (PNFSG) is = (
,
1
,
2
,
) ,here =
(N
,
)
, where N
= {n
1
, n
2
, …n
}
such that
(x)
,
1
(x),
and
1
(x)
from N to
[
0,1
]
with 0 ≤
(x)
(n
)
2
+
1
(x)
(n
)
2
+
1
(x)
(n
)
2
≤ 1
n
in N
signifies membership, indeterminacy
and non-membership functions correspondingly and
N x N where
,
2
(x)
,
2
(x)
from N xN
to
[
0,1
]
such that
(n
n
j
) ≤ α
1
(x)
(n
)
α
1
(x)
(n
j
)
2
(x)
(n
n
j
) ≤
1
(x)
(
n
)
1
(x)
(n
j
)
2
(x)
(n
n
j
) ≤
1
(x)
(
n
)
1
(x)
(n
j
)
With 0 ≤ ((
(n
n
j
))
+ (
2
(x)
n
n
j
))
+ (
2
(x)
(n
n
j
)) ≤ 1
(n
n
j
)
Definition
3.4: Complete PNFSG
A PNFSG is = (,
1
,
2
, ) where
* = (N, ) is termed as
complete PNFSG (CPNFSG)
If
α
2
(n
n
j
) =
1
(
n
)
α
1
(n
j
),
2
(n
n
j
) =
1
(x)
(
n
)
1
(x)(n
j
),
2
(x)
(n
n
j
) =
1
(x)
(
n
)
1
(x)(n
j
) for every n
,
n
j
N.
Definition 3.5
: strong PNFSG
A PNFSG = (,
1
,
2
, ) is named as
strong PNFSG if
α
2
(n
n
j
) = min ( α
1
(
n
)
, α
1
(n
j
))
2
(n
n
j
) = min (
1
(
n
)
,
1
(n
j
))
2
(n
n
j
) = max (
1
(
n
)
,
1
(n
j
))
(n
n
j
)
.
IFSG corresponding to
the Parameter e
1
IFSG Corresponding to the
parameter e
2
IFSG Corresponding to
the parameter e
3
Figure (2)
Figure (3)
Figure (4)
Pythagorean Neutrosophic Fuzzy Soft Graph
317

Definition 3.6:
Pythagorean Neutrosophic
Fuzzy soft Graph (PNFSG) and subgraph
(PNFSSG)
Let
= (
,
1
,
2
,
) with α(x),
(x),
(x) as
the membership, indeterminacy and non-
membership degree be a Pythagorean Neutrosophic
Fuzzy soft Graph
(PNFSG)
Then a Pythagorean Neutrosophic Fuzzy soft Graph
G’ = (
’
,
’
1
,
’
2
,
) with N’
N and E’
E,
(x),
(x),
(x) as the membership, indeterminacy and
non-membership is called
Pythagorean Neutrosophic
Fuzzy soft subgraph (PNFSSG)
if α
′
(x)
(
)
≤ α(x)
(
)
,
′
(x)
(
)
≤
(x)
(
)
,
′
(x)
(
)
≥
(x)
(
)
for
N.
Definition
3.7:
Intersection of
Pythagorean
Neutrosophic Fuzzy soft Graph (IPNFSG)
Let G’ = (
’
,
’
1
,
’
2
,
) , G’’ = (
’’
,
’
1
,
’
2
,
)
be Pythagorean Neutrosophic Fuzzy soft
Graph where
′*
=
(N
′
,
′
)
,
′′*
=
(N
′′
,
′′
)
with (α
′
(x),
′
(x),
′
(x)) and (α
′′
(x),
′′
(x),
′′
(x)) as their
membership, indeterminacy and non-membership
correspondingly .Then the intersection of G’ and
G’’,G=(
,
1
,
2
,
),
* =
(N,
)
is a
Pythagorean Neutrosophic Fuzzy soft Graph
where N= N’
N’’, E=E’
E’’ membership,
indeterminacy and non-membership of N and E
of for all u,v,
N such that
(i)
(
if
is in N’ and not in N’’
1
(
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ and not in N’’
(ii)
(
if
is in N’ and not in N’’
1
(
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ and not in N’’
(iii)
(
if
is in N’ and not in N’’
1
(
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ and not in N’’
(iv)
(
uv
if
is in E’ and not in E’’
2
(
uv
=
(
if
is in E’’ and not in E’
(
(
if
is in E’ and not in E’’
(v)
(
if
is in E’ and not in E’’
2
(
uv
=
(
if
is in E’’ and not in E’
(
(
if
is in E’ and not in E’’
(vi)
(
if
is in E’ and not in E’’
2
(
=
(
if
is in E’’ and not in E’
(
(
if
is in E’ and not in E’’
Definition3.8: Union of
Pythagorean
Neutrosophic Fuzzy soft Graph (UPNFSG)
Let G’ = (
’
,
’
1
,
’
2
,
) , G’’ = (
’’
,
’
1
,
’
2
,
)
be Pythagorean Neutrosophic Fuzzy soft
Graph where
′*
=
(N
′
,
′
)
,
′′*
=
(N
′′
,
′′
)
with (α
′
(x),
′
(x),
′
(x)) and (α
′′
(x),
′′
(x),
′′
(x)) as
their membership, indeterminacy and non-
membership of the vertices and edges
correspondingly. Then the union of
′
&
′′
,G =(
,
1
,
2
,
),
* =
(N,
) is a PNFSG where N =
N
′
N
′′
,
=
′
′′
and the membership,
indeterminacy and non-membership of vertices
(N), edges (E) of
for all p, q,k
N such that
Consider the following, If G = (N,E,
,
where
=
(α
1
(x)
,
1
(x)
,
1
(x)
) and
=( α
2
(x)
,
2
(x)
,
2
(x)
)
are
membership, indeterminacy and non-
membership of PNFSG
(i)
(
if
is in N’ and not in N’’
1
(k
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ or in N’’
ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,
COMMUNICATION, AND COMPUTING TECHNOLOGIES
318

(ii)
(
if
is in N’ and not in N’’
1
(
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ or in N’’
(iii)
(
if
is in N’ and not in N’’
1
(
=
(
if
is in N’’ and not in N’
(
(
if
is in N’ or in N’’
(iv)
(
pq
if pq is in E’ and not in E’’
2
(
pq
=
(
if pq is in E’’ and not in E’
(
(
if pq is in E’ or in E’’
(v)
(
if pq is in E’ and not in E’’
2
(
pq
=
(
if pq is in E’’ and not in E’
(
(
if pq is in E’ or in E’’
(vi)
(
if pqis in E’ and not in E’’
2
(
=
(
if pq is in E’’ and not in E’
(
(
if pq is in E’ or in E’’
Definition
3.8: Pythagorean Neutrosophic soft
path P (PNSP)
A Pythagorean Neutrosophic soft path P (PNSP) in
PNSFG G =(N,E,
,
where
(x)(n
i-1
,n
i
)>0 ,i = 1
to k where k is the length of the PNSP and that pair
of PNSP are called the edges.
Definition
3.9:
Longest PNSP
The diameter of , in N is the length of the
longest PNSP joining and and denoted as
(
,
)
.The strength of PNSP is represented
by
(
)
or
(
)
and defined as
(n
k−1
, n
k
)
=
(
α
2
(n
k−1
, n
k
)
,
2
(n
k−1
,
n
k
)
,
2
(n
k−1
, n
k
)
)
where n
k
N (
= 1,2, … ,
)
Definition
3.10:
pythagorean neutrosophic Soft
strength of connectedness
The pythagorean neutrosophic So ft strength of
connectedness of vertices and of PNFSG is
defined as the maximum of the strength of all PNSP’s
among and and represented by
(
,
)
.
(x,y)=(max(S(P)) where P is x-y PNSP in
G
If k≥3 and N
0
= N
n
then PNSP P is called a
Pythagorean Neutrosophic Soft Cycle(PNSC)
Example: 3.10
Let us take the follwoing PNFSG
v
1
(0.6,0.4,0.8),v
2
(0.8,0.6,0.4),v
3
(0.8,0.3,0.5),
v
4
(0.9,0.4,0.3)
e
1
(0.5,0.5,0.4),e
2
(0.6,0.4,0.2),e
3
(0.7,0.4,0.2),
e
4
(0.6,0.4,0.5)
Pythagorean Neutrosophic Soft strength of
connectedness of PNFSG
(
1
,
2
) =
(max(0.6,0.8),max(0.4,0.6),min(0.8,0.4)
= (0.8,0.6,0.4)
(
1
,
3
) =
(max(0.6,0.8),max(0.4,0.3),min(0.8,0.4)
= (0.8,0.4,0.4)
(
1
,
4
) =
(max(0.6,0.9),max(0.4,0.3),min(0.5,0.4)
=(0.9,0.4,0.4)
Definition
3.11:
pythogorean neutrosophic fuzzy
soft bridge (PNFSB)
Let =
(N,E,
,
be a PNFSG let x,y be two
vertices,
and ′ be a PNFSG of G attained by eliminate the
edge xy.
xy is a pythogorean neutrosophic fuzzy soft
bridge(PNFSB)
in G if PNCONN G’(a,b)<PNCONN G(a,b)
For some a,b.
The elimination of the edge xy decreases the
strength of connectedness among vertices in G.
Thus, xy is a PNFSB if and only if there exists
vertices a, b such that xy is an edge of each strongest
path from a to b.
Theorem 3.11
Pythagorean Neutrosophic Fuzzy Soft Graph
319

Let G =
(N,E,
,
be a PNFSG. Then the subsequent
statements are equivalent.
1. xy is a PNFSB
2. ′ (, ) <
()
3. xy is not the weakest edge of any Pythagorean
neutrosophic soft cycle (PNSC)
Proof:
2 1 If xy is not a PNFSB, t
hen ′ (, ) = (, ) ≥
().
1 3 If xy is the weakest edge of a PNSC,
then any PNSP P including the edge xy can be
converted into a PNSP
′ not involving xy but at least as strong as P,
by replacement of the PNSC as a PNSP from x to y.
Thus, xy cannot be a PNFSB.
3 2 If ′ (, ) <
(), there is a PNSP
from x to y not including xy with strength ≥
(),
and this PNSP together with xy forms a PNSC of G
in which xy is a weakest edge.
Definition
3.12:
Pythagorean neutrosphic fuzzy
soft cutvertex
Let w be any vertex and let ′ =
(N’,E’,
,
be a
PNFSSG of =
(N,E,
,
attained by removing the
vertex w. That is, ′ =
(N’,E’,
,
is the PNFSSG of
G such that
(w) = 0,
=
for all other vertices,
(w) = 0 for all vertices z, and
=
for all other
edges. Thus we call w a Pythagorean neutrosphic
fuzzy soft cutvertex in G if ′ (, ) <
(, ) for some u, v in N such that ≠ w
≠ .
Definition
3.13:
Pythagorean neutrosphic
intuitionistic fuzzy soft graph (PNIFSG)
A Pythagorean neutrosphic intuitionistic fuzzy soft
graph is
= (
, a,b, c,d, ) ,here =
(N
,
)
,
where N
= {n
1
, n
2
, …n
} such that
(x)
,
a,b
(x),
and
a,b
(x)
from N to
[
0,1
]
with 0 ≤
(x)
(n
)
2
+
a,b
(x)
(n
)
2
+
a,b
(x)
(n
)
2
≤ 1
n
in N
signifies membership, indeterminacy
and non-membership functions correspondingly and
N x N where
,
c,d
(x)
,
c,d
(x)
from N
xN to
[
0,1
]
such that
(n
n
j
) ≤ α
a,b
(x)
(n
)
α
a,b
(x)
(n
j
)
c,d
(x)
(n
n
j
) ≤
a,b
(x)
(
n
)
a,b
(x)
(n
j
)
c,d
(x)
(n
n
j
) ≤
a,b
(x)
(
n
)
a,b
(x)
(n
j
)
With 0 ≤ ((
(n
n
j
))
+ (
c,d
(x)
n
n
j
))
+
(
c,d
(x)
(n
n
j
)) ≤1
(n
n
j
)
4 CONCLUSIONS
Here in, we get some idea by applying pythagorean
neutrosophic set to fuzzy soft graph and some of its
basic definitions and properties of the pythagorean
neutrosophic fuzzy soft graphs. Here after we will
extend some other field with real time example.
REFERENCES
8. Sarala.N, Deepa.R, “The Arithmetical Edifices of
Strength of Connectedness in Intuitionistic Fuzzy Soft
Graph”, International Journal of Scientific and
Technology Research volume 9, Issue 02, February
2020. PP: 4815-4821, ISSN: 2277-8616,
Ajay.D,”Pythagorean Neutrosophic Fuzzy Graphs”,
International Journal of Neutrosophic Science,
Vil.11.No.2.PP.108-114, 2020.
Atanassov.K.”Intuitionistic Fuzzy Sets”,Fuzzy Sets and
System,Vol 20.PP.87-96,1986.
Attanassov.k, Intuitionistic fuzzy sets, Fuzzy sets and
Systems, 20(1986)87-96
Attanassov.k, Intuitionistic fuzzy sets theory and
Applications, springer-verlag, Heidelberg, 1999
Mohinda.S and Samanta.T.K, An Introduction to fuzzy soft
graph, Mathematics Moravica, 19-2(2015) 35-48.
Rosenfeld.A,Fuzzy graphs Zadeh.L.A., Tanka.K and
shimura.M, Fuzzy sets and their publications to
cognitive and decision process Academic Process, New
York,1975,75-95
Sarala.N, Deepa.R,” invention of best technology In
agriculture using intuitionstic fuzzy soft graphs”,
International Journal of Mathematical Archive-9(7),
2018, 47-57.
Sarala.N, Deepa.R,”Regular Interval valued Intuitionistic
Fuzzy Soft Graph”,The international journal of
analytical and experimental modal analysis.ISSN
NO:0886-9367.
Smarandache,F.,”A Unifying Field in Logics:Neutrosohic
Logic.Neutrosophy,Neutrosophic Set.Neutrosophic Pr
obability”,American Research Press:Rehoboth,DE,US
A,PP.1-141,1999.
Thumbakara.R.K and George.B, Soft graph, Gen.
Mathematics Notes, 21(2) (2014)75-86.
Yager.R.R.,”Pythagorean Fuzzy Subsets”, In:Proc Joint
IFSA World Congress and NAFIPS Annual Meeting
.Edmonton,Canada.PP.57-61.2013.
Yang.H.L, Notes on generalized fuzzy soft sets, Journal of
Mathematical Research and Exposition, 31(3) (2011)
567-570.
Zadeh.L. A Fuzzy sets Information and control 8(1965)
338- 353.
Zadeh.L.A.,” Fuzzy Sets”, Inform and Control, Vol.8, PP.
338-353,1965.
ICRDICCT‘25 2025 - INTERNATIONAL CONFERENCE ON RESEARCH AND DEVELOPMENT IN INFORMATION,
COMMUNICATION, AND COMPUTING TECHNOLOGIES
320
