
Proofs and Applications of Cauchy-Goursat Theorem and Cauchy’s
Integral Formula
Weilin Zhang
a
Jinqiu International, Qingdao, China
Keywords: Cauchy-Goursat theorem; Cauchy’s integral formula; Definite integrals.
Abstract: This article focuses on some basis formulae and theorems of complex analysis in further mathematics.
Complex variable function is a kind of function which contains complex number as its independent variables
on the complex plane instead of real number in the real plane. This essay attempts to prove the two theorems
found by Cauchy, i.e., Cauchy-Goursat theorem and Cauchy’s integral formula primarily and briefly by some
approaches which the people who knows the complex analysis firstly can follow and understand. After that,
there are several applications in the further mathematical aspects in this paper. This paper may contain some
reverse applications about previous conclusions and use the idea of breaking down some harsh problems into
many easier questions. This paper has gotten the steps to utilize and further understand the Cauchy-Goursat
theorem and Cauchy’s integral formula. This article may assist the people who first takes up the further
mathematics and complex analysis to realize the Cauchy-Goursat theorem and Cauchy’s integral formula and
try to construct the confidence of mastering them in the future.
1 INTRODUCTION
Complex analysis is a bit modern part of further
mathematics derived from the real analysis in 18th
century founded by a well-known mathematician
Euler. Many famous mathematics researchers have
concentrated on this area, made an effort, made up a
new idea and then finally developed a new theorem.
These include persons such as Euler, Cauchy,
Riemann, Weierstrass and so on (Chen, 2023). Their
ideas are broadly used in mechanics, electric
engineering, and pure mathematics and other
complicated aspect (Cohen, 2007). In addition, it may
be linked to the real analysis to produce a new
principle or approach in a deeper area (Zhang & Qi,
2018).
In 1825, French mathematician Cauchy pointed
out a novel theorem that the result of the integral is
independent of the shape of the integral, but has
correlation to its origin and endpoint. In 1900, another
French mathematician Goursat cut some useless
conditions down and give his proof and generalize the
theorem to a broader area. So, this theorem is known
as “Cauchy-Goursat theorem”. Next, on its
foundation, there are Cauchy’s Integral Formula to
a
https://orcid.org/0009-0001-3378-4708
solve more realistic questions. There are many
applications of other previous theorem such as
Cauchy-Riemann equation and ε-δ language to prove
the two theorems. After then, it is well-prepared to
develop the residue theorem and finally people can
get the integral of complex number (Zhou et al, 2022).
Additionally, it is also an indispensable basis of the
Taylor’s series and Laurent expansion. It is an
imperative ring of the development history of
complex analysis. Although it is complex analysis, it
will also generalize to the real analysis and serve
some problems in real function (Zhang et al, 2023).
The article will adopt the steps below to assist
readers to get to know the main body of two theorems
and popularize its influence relatively rapidly. The
article below firstly performs the two theorems,
explains them briefly and tries to give some evidence
that how Cauchy’s two findings are valid.
Furthermore, the author will introduce the
indispensable conditions needed in the theorems to
readers relatively in detail. What’s more, the paper
will focus on proving the theorem briefly by using
some methods that the mathematicians have adopted
in history and pointing out the main factor of the
method, such as breaking down the complicated
Zhang, W.
Proofs and Applications of Cauchy-Goursat Theorem and Cauchy’s Integral Formula.
DOI: 10.5220/0013861200004708
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 655-658
ISBN: 978-989-758-774-0
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
655
problems and using the old theorem reversely. In the
next step there will be some instances to assist reader
to realize and master the two conclusions. Finally, the
author will conclude the article and make the
knowledge have talked about more clearly.
2 METHODS
2.1 Cauchy-Goursat Theorem
To begin with, the author wants to introduce the
Cauchy-Goursat Theorem simply. There are three
conditions of this principle which is indispensable.
Without the three conditions, the formula is not valid
so that these conditions must be followed. Firstly, Ω
is a simply connected subset of the complex plane.
What’s more,
is an analytic function of the
variable z. In addition, γ is a simply closed curve in
Ω. Then if one integrates the function
along the
curve γ, people will get the conclusion that
To prove this, the definition of the term “simply
connected” and “simply closed” are imperative.
Simply connected area means that any area in the
curve surrounding Ω belongs to Ω. In other words,
there isn’t any hole occurring in the area Ω. If the
curve is closed without cross with itself, people
consider it as a simply closed curve.
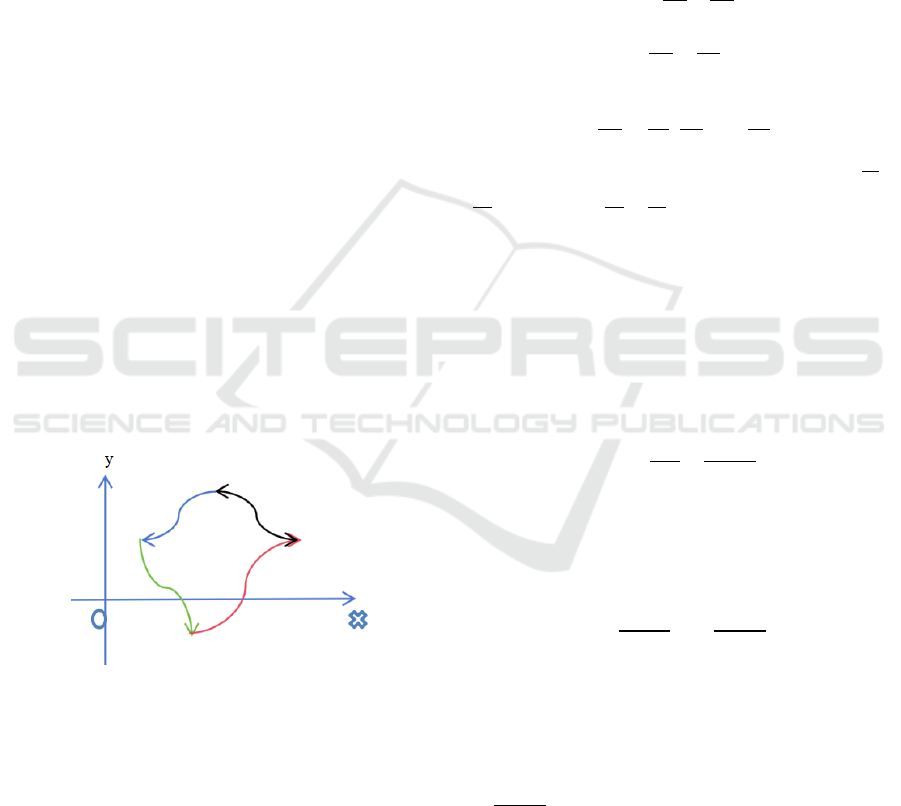
Figure 1: Illustration of the Green’s theorem
Then it is enough to gather all conditions to prove
the Cauchy-Goursat theorem. The mathematicians
usually break any complex function
to the
imaginary part and real part
Due to , it is calculated that
Then, people usually use the Green’s formula
reversely to attempt to prove the result of the integral
is zero. Green’s formula used the idea that breaks a
complicated problem to many simple problems so one
can solve each simple problem then add them up to
find the final conclusion. Green divided one integral
to four integrals, the upper one (blue), the lower one
(red), the right one (black) and the left one (green),
like the plot shown in Figure 1. According to the
breaking, there are some lines have no contribution to
the integral. Then Green got his formula
By adopting Cauchy-Riemann Function, one finds
In light of this formula, it is found that
. Finally, formula
shown in Eq. (1) can be obtained. This finishes the
proof of the theorem.
2.2 Cauchy’s Integral Formula
By using the idea of Cauchy-Goursat theorem, the
Cauchy’s integral formula is found below to cope
with more specific problems and the theorem is from
theories to the realistic.
It also uses the idea of breaking the only one integral
to 4 integrals to prove that as long as both the outer
contour and the inner one are closed, the integrals
along the two contours are equal to each other (Egahi
& Otache, 2018). The formula below can be got as
Due to the
is analytic in
, for given any
small number , there must exist a number
that when
, when
belongs to the contour , so that
. Consequently, the formula is arrived
Since the term behind tends to zero, the result of the
integral is
.When someone move some of
terms to the left-hand side, the conclusion upper will
be bringing out.
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
656

When using the Cauchy’s integral formula, people
should consider that
is the only one strange point in
the contour (Mihálka, et al, 2019). In other words, if
there are two strange points in the contour, the
Cauchy’s integral formula can’t be used to solve the
problem directly and should adopt a further formula
to solving that. It is called residue theorem and it
stemmed from this theorem.
3 RESULTS AND APPLICATIONS
3.1 Complex Applications
As people all known, the complex variables have
many applications in various aspects. It is no
exception to the Cauchy-Goursat theorem and
Cauchy’s integral formula. During the paragraph
below, the readers will know the utilization of these
theorems. It is not only used in the problem-solving,
but also adopted in the novel theorems, such as
Laurent’s expansion, Taylor’s series and the residue
theorems.
This part will focus on the application of Cauchy’s
integral formula in the complex analysis. The author
will use two example to distinguish two situation that
where the Cauchy’s integral formula can be used or
there is a translation needed to further theorem
adopted.
Example 1.
, when
.
It is clear to see that the contour C is a circle
whose centre is , and radius is
laying on the
complex plane. Its upper boundary of the circle is
,
while the lower boundary of the circle is
. Thus,
there are two strange points situating on the complex
plane, which is
and
. Due to
is the
only one strange point in the contour C, it is suitable
for the situation that Cauchy’s integral formula is
valid.
Hence if Cauchy’s integral formula is adopted, the
result can be gotten directly. This is also proved
indirectly that the Cauchy’s integral is valid when
there is only one strange point in the contour.
Example 2.
, when
.
The contour is same as the last example, but now
there are three strange points in the complex plane,
which are 0,
,
. There are two strange points
locating in the contour C: 0 and
. So, the
Cauchy’s integral formula is not appropriate for this
situation. Some people would say it needs residue
theorems to perform a further calculation. However,
residue is the numerator actually the partial fraction
of a complicated fraction. In others words, the
complicated fraction should be turned to two simple
fractions so that the Cauchy’s integral formula could
be adopted on it. Two parameters, the capital A and
capital B like below are supposed to adopted to
complete the partial fraction (Zhu & Luo, 2023). The
partition is given by
In order to calculate the capital A and capital B
easily, on the next step each side could multiply the
term
, i.e.,
.
Thus, one can finally let z equal to 0 and
one
by one. When z equal to zero, the formula below can
be gotten and A will be
, i.e.,
. This
finishes the calculation of A and B.
When equal to the other critical value,
,
the formula below can be obtained and B will be -
since
. Hence the partial fraction is
completed and the critical values or residues have
been gained. Then the formula could be transferred to
a more clearly term:
Consequently, the formula could be written as the
formula below which the Cauchy’s integral formula
could be adopted and further calculation could
complete:
The second example provides evidence of the
universality of the Cauchy’s integral formula. It
proved that the Cauchy’s integral formula could be
adopted to calculated a sophisticated integration that
two, or of cause more strange points exists in the
contour and show the principle that how the residue
theorem works (Yang & Zhang, 2006).
Proofs and Applications of Cauchy-Goursat Theorem and Cauchy’s Integral Formula
657

3.2 Real Applications
The complex analysis could be spread to real analysis.
This may assume that the Cauchy’s integral formula
could also be spread to real situation.
However, some people may argue that how the
extrapolation could be valid. As everybody all known,
the complex number contain two parts, the imaginary
parts and the real parts. Hence if there is a demand to
spread the complex analysis to the real analysis, it
must be the binary real function. In real plane, the
integral of a simple closed curve is 2. Similarly, the
integral of a simple closed curve in complex plane is
2. It is clear that there is a relationship between the
results in complex plane and that in real plane.
When breaking the complex function into two
parts, it can transfer to the following terms which are
divided into several parts:
where
and
. According to Cauchy’s integral
formula, the results of integration is 2 .
Consequently, one can get that the real part of the
integration is zero, and the imaginary part is 2
Just use the steps above, the promotion of a
complex theorem to application in real function is
finished. Promotion is a necessary process in science
research, abundance principle is found by this method
that from common to specific, from one hand to
another hands. The researcher should not only realize
the nature of the principle, but also need to open their
mind to link things in distinct areas together and find
their correlation (Ji, 2023).
4 CONCLUSIONS
This article aims to assist the beginner to understand
the two indispensable theorem in complex analysis,
Cauchy-Goursat theorem and Cauchy’s integral
formula. From their conditions to their proof, the
author has adopted appropriate words to introduce the
principle in detail. Then the article referred what
situations the principle could be used in complex
analysis and real analysis. In complex analysis, the
author calculated two similar integrals with distinct
characteristics to show that how to integrate a formula
with only one strange point or two or more strange
points, prepared for the proof and application of
residue theorems in the next. On the other hand, the
theorem is spread from complex analysis to real
analysis, it could inspire the ideas of generalization of
more new theorems in the future.
However, there are still plenty of drawbacks exists
in the article needed to be enhanced and corrected,
such as the grammar, the accuracy of the words.
Moreover, as it is a mathematics paper, the proof is
supposed to be more rigorous and in detail. If the
reader thinks anywhere has shortage, don’t be shy to
contact the author and have a communication. It is my
honour to accept contact and correction. In the future,
the author will read the authority complex variables
mathematics textbook and think carefully, then
concentrated on the further complex analysis, prove
and apply the Taylor’s series, Laurent expansion, and
residue theorems.
REFERENCES
Chen, W., Zhang, D., & Zou, Y. (2023). Complex number
and its discovery history. Highlights in Science,
Engineering and Technology, 38, 168–173. 38, 168–
173.
Cohen, H. (2007). Complex analysis with applications in
science and engineering. Springer.
Egahi, M., & Otache, O. I. (2018). Deriving Cauchy's
integral formula using division method. Nigerian
Annals of Pure and Applied Sciences, 1, Article 32.
Ji, Z. S. (2023). Mathematical generalization: Patterns,
methods, and educational value. Training for Primary
and Secondary School Teachers, (3), 29-34.
Mihálka, Z. É., Szabados, Á., & Surján, P. R. (2019).
Application of the Cauchy integral formula as a tool of
analytic continuation for the resummation of divergent
perturbation series. The Journal of Chemical Physics,
150(3), 031101.
Yang, L., & Zhang, W. W. (2006). Applications of
Cauchy's integral formula. Journal of Cangzhou Normal
College, (3), 64-65+67.
Zhang, Z. X., Du, X. R., & Ma, Y. L. (2023). Generalization
of a class of generalized integrals using the residue
theorem. Physics and Engineering, 33(04), 12-17.
Zhang, X., & Qi, J. (2018). The real extension of Cauchy's
integral formula. Journal of Ili Normal University
(Natural Science Edition), 12(4), 12–16+86.
Zhou, W. P., Liu, Y. F., & Song, T. L. (2022). Two types
of infinite integrals solved by the residue theorem.
Physics and Engineering, 32(01), 56-59.
Zhu, J.-M., & Luo, Q.-M. (2023). Partial-fraction
decomposition of a rational function and its
application. Advances in Continuous and Discrete
Models, 2023, Article 1.
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
658
