Estimation of Rate-Dependent Hammerstein Model

of Piezo Bender Actuator

Lenka Kukli

sov

a Pavelkov

The Czech Academy of Sciences, Institute of Information Theory and Automation

Pod Vod

arenskou v

ı 4, 182 00, Prague 8, Czech Republic

Keywords:

Rate-Dependent Hysteresis, Hammerstein Model, ARX Model, Particle Swarm Optimization, Splines,

Piezoceramic Actuator.

Abstract:

The paper presents a Hammerstein model of a commercial piezoelectric bender PL140 from Physik Instru-

mente Co. The model consists of a nonlinear static part that describes the inherent hysteresis and a linear

dynamic part that is represented by the auto-regressive model with exogenous input. The linear model pa-

rameters are estimated one-time using a particle swarm optimization algorithm. The rate-dependent nonlinear

part is identiﬁed using input voltage data, along with a hidden variable that is obtained with the help of the

inverted linear part. The experimental data are generated by a PL140 Simscape model with parameters set in

accordance with catalog data.

1 INTRODUCTION

Piezoelectric actuators (PEAs) are essential in the

ﬁeld of modern science and engineering. Their high

resolution and fast response distinguish them from

other actuator types, such as shape-memory alloys.

This makes them invaluable in a wide range of appli-

cations, including precision positioning in manufac-

turing, microﬂuidics control, medical ultrasonic ther-

apy, and robotics (Zhou et al., 2024).

A signiﬁcant challenge in PEAs is the hysteresis

effect, a nonlinear relationship between input voltage

and output displacement. This nonlinearity depends

on input voltage amplitude and rate, causing position-

ing errors of 10-15% or higher at increased frequen-

cies. It can degrade system performance and poten-

tially lead to instability (Yuan et al., 2024).

To address the hysteresis problem, various math-

ematical models have been developed. These can

be categorized into physics-based models and phe-

nomenological models. Physics-based models are de-

rived from the fundamental physical principles of the

material but are often complex and not universally ap-

plicable (Yuan et al., 2024).

Phenomenological models employ mathematical

representations to characterize observed hysteresis ef-

fects, often without offering a physical explanation.

https://orcid.org/0000-0001-5290-2389

They can be categorized into the following method-

ological groups: operator-based models, differential-

equation-based models, and other models. Operator-

based models deﬁne hysteresis through a composition

of elementary memory operators. This approach al-

lows for high accuracy but can lead to increased com-

putational complexity. The most popular models in-

clude Preisach model, Krasnosel’skii-Pokrovkii (KP)

model, Prandtl-Ishlinskii (PI) model, and Maxwell

Model (Yuan et al., 2024). Differential-equation

based models describe hysteresis through differen-

tial equations that capture the memory-dependent be-

haviour of PEAs. The main representatives are Bouc-

Wen model, Duhem model, and Dahl model (Dai

et al., 2023; Yuan et al., 2024). Other methods in-

clude models such as neural networks (Son et al.,

2021), Gaussian processes (Meng et al., 2022) or

polynomial-based models (Yang et al., 2020).

Models can also be categorized according to

whether their behavior is inﬂuenced by the rate of

change of the input voltage. Rate-independent models

are suitable for low-frequency inputs. They are val-

ued for simplicity and low computational cost, though

inadequate for dynamic conditions. Rate-dependent

models better capture high-speed behavior. They are

suitable for integration into advanced control schemes

(Gan and Zhang, 2019).

The above mentioned phenomenological models

are predominantly static. To capture a dynamic be-

532

Kuklišová Pavelková, L.

Estimation of Rate-Dependent Hammerstein Model of Piezo Bender Actuator.

DOI: 10.5220/0013855300003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd Inter national Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 532-538

ISBN: 978-989-758-770-2; ISSN: 2184-2809

havior, it is convenient to use the Hammerstein model

that offers a structured, phenomenological approach

to modeling hysteresis by decoupling the static non-

linear hysteresis characteristics from the dynamic be-

havior of the system (Dai et al., 2023). This model

consists of two parts connected in series: a static non-

linear component that captures the hysteresis effects

and a linear dynamic block that reﬂects the system’s

dynamic response.

This method provides a signiﬁcant degree of ﬂex-

ibility. The nonlinear block can be represented by

any of the above mentioned phenomenological mod-

els making the Hammerstein model adaptable to di-

verse hysteresis behaviours (Dai et al., 2023).

From now on, we will focus on the Hammerstein

model of a piezo actuator with a rate-dependent non-

linear static part. In this context, the static nonlin-

earity is usually described by the Bouc-Wen model.

In (Zhang et al., 2021) and (Barbosa et al., 2020),

it is coupled with auto-regressive exogenous (ARX)

model, in (Liu et al., 2023), with a mass-spring-

damper system and in (Yang et al., 2022), with a frac-

tional dynamic model. Modiﬁed PI model together

with online inﬁnite impulse response is used in (Yi

et al., 2022). In (Zhang et al., 2023), a static Preisach

model and a dynamic transfer function are combined.

In (Jin et al., 2024), Hammerstein model consists of

an optimized composite neural network and an auto-

regressive exogenous model in series.

Here, we will focus on a rate-dependent Hammer-

stein model of a speciﬁc piezo actuator, the PL140

model from Physik-Instrumente. We will build on

a recently published study (Pavelkov

a Kukli

sov

a and

Belda, 2024) that describes the mentioned piezo actu-

ator using an Hammerstein model but does not con-

sider rate dependency. We will extend the model ap-

plicability to rate-dependent scenarios. Our aim is to

build a simple and reliable algorithm that can be eas-

ily integrated into a control system with piezoelectric

actuator.

2 HAMMERSTEIN MODEL

This section presents a rate-dependent Hammerstein

model of a piezo bender actuator a its estimation.

A discrete time Hammerstein model is a well-

established framework for data-driven PEA descrip-

tion. It consists of a nonlinear static part serially

connected with a linear dynamic part, see Figure 1.

The block NLS describes the static hysteresis non-

linearity and the block LD describes the linear dy-

namic characteristic of the piezoelectric actuator.

In general, the linear and nonlinear parts of the

Figure 1: Block diagram of Hammerstein model – NLS

corresponds to a static non-linearity, LD represents a lin-

ear dynamic behavior, u

, z

, ε

, and y

are an input, hidden

non-measurable variable, noise, and output, respectively;

t ∈ {1,2,··· ,t} denotes a discrete time.

Hammerstein model are coupled during the identiﬁ-

cation process. However, under particular conditions,

they can be identiﬁed separately (Bai, 2004). If the

system is excited by an input in the form of pseudo-

random binary sequences (PRBS) with sufﬁciently

small amplitude, then non-linearity is not activated.

As a result, it holds z

∼ u

. The linear part LD can

therefore be identiﬁed independently.

Subsequently, after the excitation with a “rich”

signal, the inverse LD model can be used to estimate

the hidden variable z

. Then, based on this and using

knowledge of the input, it is possible to identify the

NLS part.

2.1 Estimation of LD Part

The LD part of Hammerstein model, Figure 1, can be

represented by an auto-regressive model with external

input (ARX model) (Dai et al., 2023).

Here, we consider a 2

order ARX model, as it is

an accepted method to represent electro-mechanical

systems (Wilkie et al., 2002). It is deﬁned as follows

= ψ

θ + ε

(1)

where

t ∈ {1,2, ·· · ,t} denotes discrete time,

is an observable output,

is an optional known input,

= [y

t−1

, y

t−2

, u

t−1

, u

t−2

]

is the regression

vector,

θ = [a

, a

, b

]

, is the vector of unknown

regression coefﬁcients,

T denotes the transposition,

is a white noise, independent and identically dis-

tributed.

The least square (LS) method is typically used

to estimate the ARX model (1) parameters, espe-

cially when the parameters need to be estimated re-

cursively (Ljung, 1998). Here, we only need a one-

time estimate of this model. We will use the parti-

cle swarm optimisation (PSO) method (Shi and Eber-

hart, 1998), which is simple to implement, ﬂexible

Estimation of Rate-Dependent Hammerstein Model of Piezo Bender Actuator

533

and more robust comparing to recursive LS (Jahan-

dideh and Namvar, 2012).

Note that recently, the PSO method was used

in the context of a Hammerstein rate-dependent dy-

namic hysteresis modeling to calculate the parameters

of the Bouc-Wen model (Fu et al., 2024).

PSO is an algorithm that simulates social behav-

ior, such as a ﬂock of birds, to ﬁnd optimal solutions

to problems. It uses a swarm of S particles, where

each particle goes around a D-dimensional problem

space and represents a potential solution. In PSO, par-

ticles adjust their positions based both on their own

experience and the experience of the entire group.

Each particle maintains a velocity vector v

and a po-

sition vector x

, where index m = 1,2, ···, S.

PSO estimation starts with a random initialization

of vectors v

and x

. In each iteration, the value of

a given ﬁtness function f is used to update the best

solution for each particle as well as the best solu-

tion for the whole swarm. The PSO estimation ter-

minates when either the global optimum or the maxi-

mum number of iterations is reached.

The evolution of a velocity and a position of m-th

particle at the i-th iteration is as follows:

m,i+1

= w

m,i

+ c

1,i

bm,i

− x

m,i

)

+ c

2,i

− x

m,i

) (2)

m,i+1

= x

m,i

+ v

m,i+1

(3)

where i means iteration, w represents inertia weight,

is a cognitive acceleration parameter, c

is a so-

cial acceleration parameter, r

, r

∈ ⟨0, 1⟩ are random

numbers, p

bm,i

is the best location found by the m-th

particle and g

is the global best location of all the

particles at the i-th iteration. The best locations are as

follows:

bm,i



bm,i−1

, if f (x

m,i

) ≥ f (p

bm,i−1

)

m,i

, if f (x

m,i

) < f (p

bm,i−1

)

= arg min

m,i

f (x

m,i

), 1 ≤ m ≤ S (4)

The tuning parameters of PSO algorithm, i.e. c

, c

and w maintain the balance between global discov-

ery and local detection. We have used the follow-

ing approved setting (Fang et al., 2023; Belda and

Pavelkov

a Kukli

sov

a, 2023) that prevent a trapping

PSO in a local minima:

• time-varying acceleration coefﬁcients

1,i

= 2.5 − 2 i/α (5)

2,i

= 0.5 + 2 i/α (6)

where α denotes the total number of iterations.

• linearly decreasing inertia weights

= w

max

− (w

max

− w

min

)i/α (7)

where w

max

and w

min

denote the maximal

and minimal inertia weight, respectively.

The algorithmic summary of the ARX model (1) esti-

mation using PSO is as follows:

1) Initialise the PSO algorithm parameters,

i.e., the swarm size S, inertia weight w,

acceleration coefﬁcients c

, c

, maximum

number of iterations α, and maximum

velocity V

max

2) Set a swarm of S particles of dimension D = 5

that corresponds to the size of θ in (1).

3) Initialise the position x

m,1

and velocity v

m,1

and p

bm,1

of each particle (m = 1, 2, · ·· , S);

and initialise g

of the swarm.

4) Calculate each particle’s ﬁtness f value that corre-

sponds to the absolute prediction error

f =

∑

i=1

|y(i) − ψ

5) Update best local position p

bm,i

and global posi-

tion g

according to (4).

6) Update velocity v

m,i

(2) and position x

m,i

(3)

of each particle.

7) If either iterations number α or ﬁtness f value

reaches the threshold then END, else GO to the

step 4).

2.2 Estimation of NLS Part

The NLS part of the Hammerstein model, Figure 1,

can be identiﬁed with the help of a data set u

and

. Inputs u

are available. Hidden variables z

can be

estimated from corresponding outputs y

by the help

of the inverted LD part, i.e., ARX model (1), obtained

in the previous step (Bai, 2004; Pavelkov

a Kukli

sov

and Belda, 2024).

The inverted ARX model (1) with input y

and out-

put z

, neglecting the noise term, has the following

form:

− a

t−1

− a

t−2

− b

t−1

− b

t−2

)

(8)

where a

, a

, b

and b

correspond to the regres-

sion parameters of the ARX model (1).

Using an inverse model (8) and outputs y

, that are

obtained as responses to “rich” inputs u

, i.e., inputs

that sufﬁciently excite the hysteresis of the identiﬁed

PEA, a hidden variable z

can be estimated.

Then, the NLS block of Hammerstein model, Fig-

ure 1, can be identiﬁed based on generated inputs u

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

534

together with estimated hidden variables z

. The pro-

cess of identifying hysteresis is as follows. We have

a pair of data points [u,z] that form a hysteresis loop

when graphically displayed. First, we split this loop

into two parts to obtain two sets of values correspond-

ing to two nonlinear functions, an “upper” one and

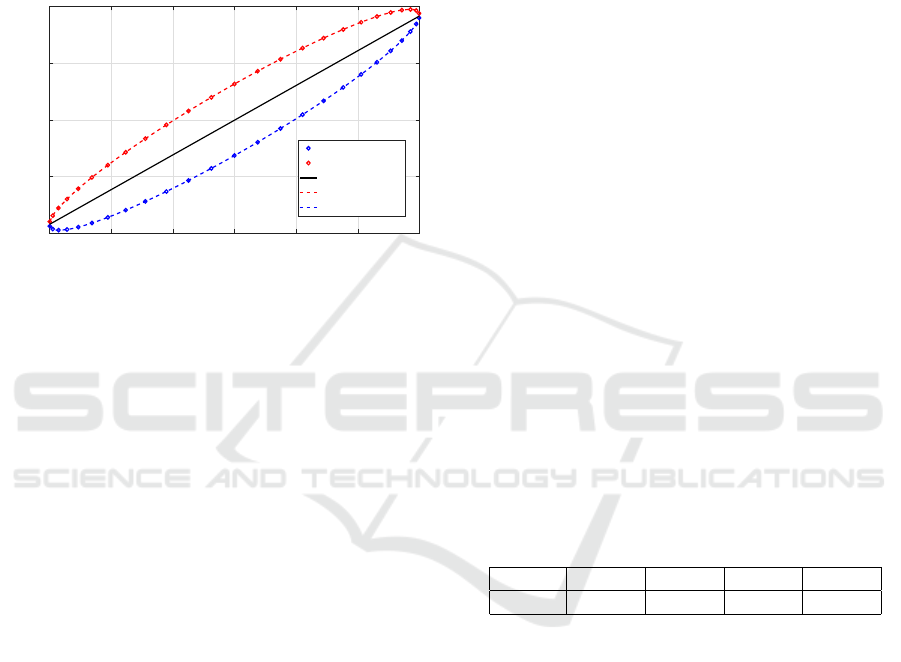
a “lower” one, see an illustrative example in Fig. 2.

Then, we can interpolate the points in both sets using

splines (De Boor and De Boor, 1978).

-30 -20 -10 0 10 20 30

-200

-100

100

200

lower data

upper data

separating line

lower spline

upper spline

Figure 2: Data pairs [u,z] for estimation of NLS block of

Hammerstein model divided to the lower (blue) and upper

(red) parts with separating line depicted.

Having two nonlinear functions, the identiﬁed

NLS block performs as follows:

- if u

> u

t−1

, then the value z

is read from the “up-

per” function,

- otherwise, it is read from the “lower” function.

2.3 Estimation Summary

Consider the Hammerstein model of PEA in Figure 1.

Then, the estimation is as follows:

1) Generate outputs y

by stimulating identiﬁed PEA

with PRBS.

2) Estimate the parameters of the LD block in

Hammerstein model, Fig. 1, represented by the

ARX model (1) using PSO algorithm in Sec-

tion 2.1 using the PRBS data.

3) Generate outputs y

by stimulating identiﬁed PEA

with “rich” data, e.g. sin waveform.

4) Estimate z

in Hammerstein model, Fig. 1, accord-

ing to (8) using y

from 3) as inputs.

5) Identify the NLS block in Hammerstein model as

described in Subsection 2.2 using input data u

from 3) and output data ˆz

from 4)

6) Generate new “rich” data set as described in 3) to

test the identiﬁed Hammerstein model accuracy.

3 EXPERIMENTS

In this section, the Hammerstein model, Fig-

ure 1, of the piezo bender actuator PL140 (Physik-

Instrumente, 2025) is identiﬁed. The data for esti-

mation are obtained using a “digital twin” of the real

bender that is realized as a Simulink/Simscape model

(Pavelkov

a Kukli

sov

a and Belda, 2024). Material

constants are set according to the catalog data.

Experiments were performed for various frequen-

cies of input signal. The sampling period was set

= 5 × 10

−4

s. Note that the estimation of the

LD part of Hammerstein model is rate-independent.

The parameter estimation of the corresponding ARX

model is therefore performed only once. The ﬁxed

inverse model is then used continuously for the calcu-

lation of a rate-dependent non-linearity.

Estimated parameters of the ARX model (1) that

represents the LD part are presented in Table 2. The

estimation process for 500 iterations of PSO algo-

rithm (see Section 2.1) is shown in Figure 3.

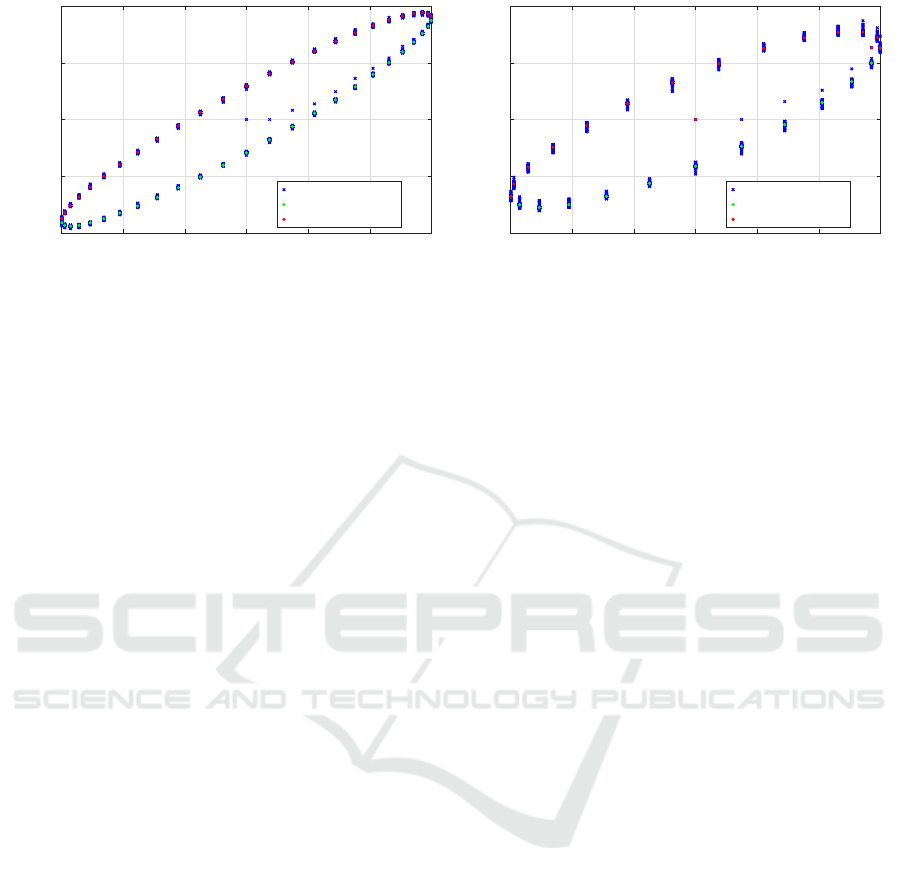
Estimated hysteresis loops for various frequencies

of input signal are depicted in Figures 4 and 5. The

Figures show how the loops are split in two parts

corresponding to the values of two nonlinear func-

tions. The interpolation by splines as described in

Section 2.2 is done using Matlab function spline.

The performance of the identiﬁed Hammerstein

model was tested by a periodic step-wise signal of

various frequency. The mean square error between

simulated and predicted outputs for various frequen-

cies are summarized in Table 1.

Table 1: MSE.

f (Hz) 5 20 40 80

MSE 0.0129 0.0155 0.0180 0.0322

4 CONCLUSIONS

This paper presents an approach for modeling the

rate-dependent hysteresis behavior of the piezoelec-

tric bender actuator using a Hammerstein model

structure. The main contribution is in incorporating

a rate-dependent nonlinear static (NLS) block repre-

sented by two spline functions. Since the proposed

model can be easily estimated, it has the potential to

be used for model predictive control.

The experiments demonstrate that the Hammer-

stein model is suitable for capturing the hysteresis

characteristics of the actuator across different input

frequencies. The proposed method separates the esti-

mation of the LD and NLS parts. The proposed model

Estimation of Rate-Dependent Hammerstein Model of Piezo Bender Actuator

535

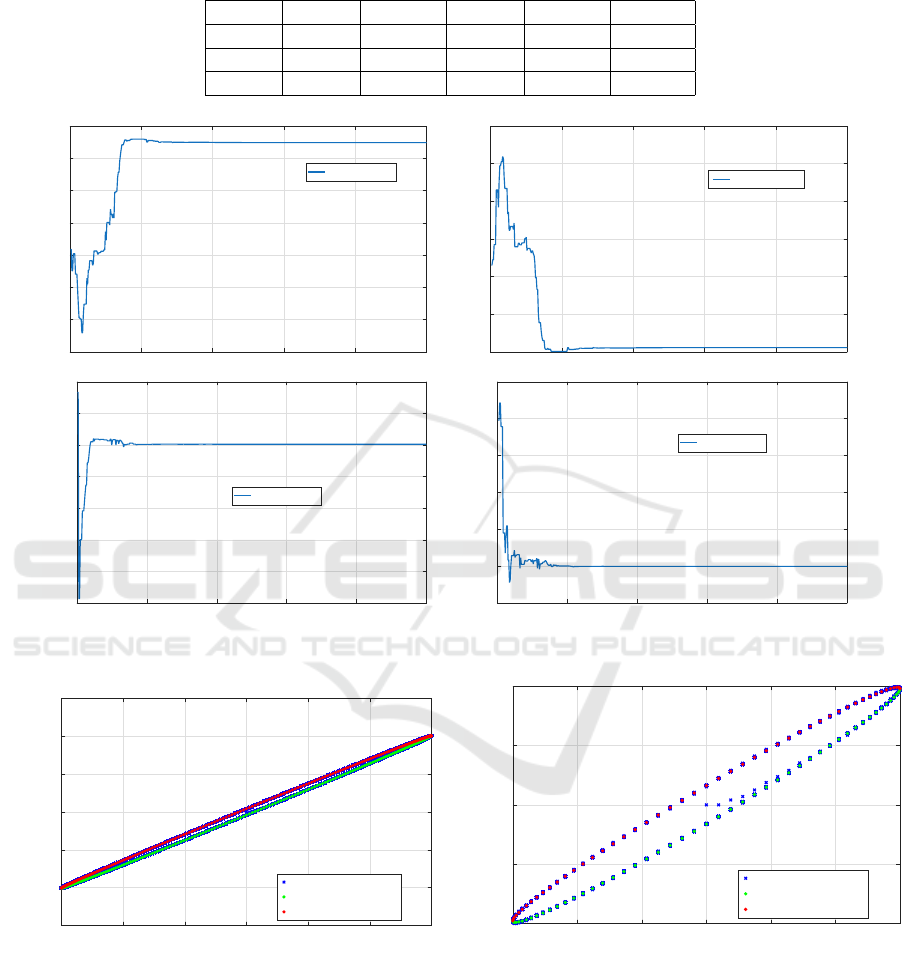
Table 2: Estimated regression coefﬁcients of the ARX model representing the LD part of Hammerstein model depending on

the frequency f of input sine signal.

f (Hz) a

5 1.7424 -0.9453 0.0012 -0.0004 -0.0003

50 1.7424 -0.9453 0.0011 -0.0004 -0.0003

80 1.7424 -0.9453 0.0011 -0.0004 -0.0003

0 100 200 300 400 500

-1.5

-1

-0.5

0.5

1.5

estimate

0 100 200 300 400 500

-1

-0.5

0.5

1.5

estimate

0 100 200 300 400 500

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

estimate

0 100 200 300 400 500

-0.05

0.05

0.1

0.15

0.2

0.25

estimate

Figure 3: The courses of parameter estimation of the ARX model (1) for 500 iterations of the PSO algorithm.

u (V)

-30 -20 -10 0 10 20 30

-300

-200

-100

100

200

300

hysteresis curve

lower reduced part

upper reduced part

u (V)

-30 -20 -10 0 10 20 30

-200

-100

100

200

hysteresis curve

lower reduced part

upper reduced part

Figure 4: Hysteresis curve representing a NLS part of Hammerstein model of PL140 (blue) with indicated averaged upper

(red) and lower (green) parts for f = 5 Hz (left) and f = 20 Hz (right).

yields a consistent performance across frequencies up

to ca 80 Hz. For higher frequencies, the error grew

rapidly. The resonance frequency of PL140 is 160 Hz.

Above this frequency, the estimated hysteresis curve

even became inverted. The cause may be both the

simplicity of the presented model and problems re-

lated to the sampling period. This could be a topic for

the further research, together with the testing on a real

piezo actuator.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

536

u (V)

-30 -20 -10 0 10 20 30

-200

-100

100

200

hysteresis curve

lower reduced part

upper reduced part

u (V)

-30 -20 -10 0 10 20 30

-200

-100

100

200

hysteresis curve

lower reduced part

upper reduced part

Figure 5: Hysteresis curve representing a NLS part of Hammerstein model of PL140 (blue) with indicated averaged upper

(red) and lower (green) parts for f = 40 Hz (left) and f = 80 Hz (right).

REFERENCES

Bai, E.-W. (2004). Decoupling the linear and nonlinear

parts in Hammerstein model identiﬁcation. Automat-

ica, 40(4):671–676.

Barbosa, M. P. S., Rakotondrabe, M., and Ayala, H. V. H.

(2020). Deep learning applied to data-driven dynamic

characterization of hysteretic piezoelectric microma-

nipulators. IFAC-PapersOnLine, 53(2):8559–8564.

Belda, K. and Pavelkov

a Kukli

sov

a, L. (2023). Particle

swarm optimisation for model predictive control adap-

tation. page 144 – 149.

Dai, Y., Li, D., and Wang, D. (2023). Review on the non-

linear modeling of hysteresis in piezoelectric ceramic

actuators. Actuators, 12(12).

De Boor, C. and De Boor, C. (1978). A practical guide to

splines, volume 27. springer New York.

Fang, J., Liu, W., Chen, L., Lauria, S., Miron, A., and

Liu, X. (2023). A survey of algorithms, applications

and trends for particle swarm optimization. Interna-

tional Journal of Network Dynamics and Intelligence,

2(1):24–50.

Fu, Y., Gao, S., Li, L., Chen, C., and Melnikau, S. (2024).

Rate-dependent hysteresis modeling of piezoceramic

actuators and parameter identiﬁcation with an im-

proved genetic algorithm. In 2024 9TH INTERNA-

TIONAL CONFERENCE ON ELECTRONIC TECH-

NOLOGY AND INFORMATION SCIENCE, ICETIS

2024, pages 82–86.

Gan, J. and Zhang, X. (2019). A review of nonlinear hys-

teresis modeling and control of piezoelectric actua-

tors. AIP Advances, 9(4).

Jahandideh, H. and Namvar, M. (2012). Use of pso in pa-

rameter estimation of robot dynamics; part two: Ro-

bustness. In 2012 16th International Conference on

System Theory, Control and Computing (ICSTCC),

pages 1–6.

Jin, J., Sun, X., and Chen, Z. (2024). Inverse feedfor-

ward control of piezoelectric actuators using opti-

mized composite neural network-based hammerstein

model. JOURNAL OF INTELLIGENT MATERIAL

SYSTEMS AND STRUCTURES, 35(20):1558–1575.

Liu, D., Dong, J., Guo, S., Tan, L., and Yu, S. (2023). Pa-

rameter identiﬁcation of model for piezoelectric actu-

ators. Micromachines, 14(5):1050.

Ljung, L. (1998). System Identiﬁcation: Theory for the

User. Pearson Education.

Meng, Y., Wang, X., Li, L., Huang, W., and Zhu, L.

(2022). Hysteresis modeling and compensation of

piezoelectric actuators using gaussian process with

high-dimensional input. In Actuators, volume 11,

page 115. MDPI.

Pavelkov

a Kukli

sov

a, L. and Belda, K. (2024). Identiﬁca-

tion of piezoelectric actuator using bayesian approach

and neural networks. In Proceedings of the Interna-

tional Conference on Informatics in Control, Automa-

tion and Robotics, volume 1, page 591 – 599.

Physik-Instrumente, S. E. (2025). PICMA Bender PL112

- PL140 Datasheet. https://www.physikinstrumente.

com/en/products/piezoelectric-transducers-actuators/

pl112-pl140-picma-bender-103000. [Accessed

22-07-2025].

Shi, Y. and Eberhart, R. (1998). A modiﬁed particle swarm

optimizer. In IEEE Int. Conf. on Evolutionary Com-

putation Proceedings. IEEE World Congress on Com-

putational Intelligence, pages 69–73.

Son, N. N., Van Kien, C., and Anh, H. P. (2021). Hysteresis

compensation and adaptive control based evolution-

ary neural networks for piezoelectric actuator. Inter-

national Journal of Intelligent Systems, 36(10):5472–

5492.

Wilkie, J., Johnson, M., and Katebi, R. (2002). Simple sys-

tems: second-order systems, pages 173–195. Macmil-

lan Education UK, London.

Yang, C., Verbeek, N., Xia, F., Wang, Y., and Youcef-

Toumi, K. (2020). Modeling and control of piezoelec-

tric hysteresis: A polynomial-based fractional order

disturbance compensation approach. IEEE Transac-

tions on Industrial Electronics, 68(4):3348–3358.

Yang, L., Zhao, Z., Zhang, Y., and Li, D. (2022). Rate-

dependent modeling of piezoelectric actuators for

nano manipulation based on fractional hammerstein

model. MICROMACHINES, 13(1).

Yi, S., Zhang, Q., Xu, L., Wang, T., and Li, L. (2022).

Estimation of Rate-Dependent Hammerstein Model of Piezo Bender Actuator

537

Hysteresis online identiﬁcation approach for smart

material actuators with different input signals and

external disturbances. NONLINEAR DYNAMICS,

110(3):2557–2572.

Yuan, Z., Zhou, S., Zhang, Z., Xiao, Z., Hong, C., Chen,

X., Zeng, L., and Li, X. (2024). Piezo-actuated smart

mechatronic systems: Nonlinear modeling, identiﬁ-

cation, and control. MECHANICAL SYSTEMS AND

SIGNAL PROCESSING, 221.

Zhang, M., Cui, X., Xiu, Q., Zhuang, J., and Yang, X.

(2023). Dynamic modeling and controlling of piezo-

electric actuator using a modiﬁed preisach operator

based hammerstein model. INTERNATIONAL JOUR-

NAL OF PRECISION ENGINEERING AND MANU-

FACTURING, 24(4):537–546.

Zhang, Q., Gao, Y., Li, Q., and Yin, D. (2021). Adaptive

compound control based on generalized bouc–wen in-

verse hysteresis modeling in piezoelectric actuators.

Review of Scientiﬁc Instruments, 92(11).

Zhou, X., Wu, S., Wang, X., Wang, Z., Zhu, Q., Sun, J.,

Huang, P., Wang, X., Huang, W., and Lu, Q. (2024).

Review on piezoelectric actuators: materials, classiﬁ-

cations, applications, and recent trends. Frontiers of

Mechanical Engineering, 19(1):6.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

538