
An Adaptive-Robust Strategy Design for Process Control
Dumitru Popescu
1,2
, Catalin Dimon
1
and Pierre Borne
3
1
Department of Automatic Control and Systems Engineering, University Politehnica of Bucharest,
Splaiul Independentei 313, Bucharest, Romania
2
Academy of Romanian Scientists, Strada Ilfov 3, Bucharest, Romania
3
Centre de Recherche en Informatique, Signal et Automatiqe de Lille, Ecole Centrale de Lille, Villeneuve d’Ascq, France
Keywords: Adaptive Control, Robust Control, Adaptive-Robust Control, Design Methodology, Model Degradation,
Optimal Control.
Abstract: The paper presents a new design strategy for industrial process control applications. The adaptive-robust
control approach considers both adaptive control advantages and robust control benefits; the connection
between the two concepts preserves the imposed performances for the closed loop nominal control system.
The combined adaptive-robust solution introduces the same integral criterion for parameters identification of
the process and for the control algorithm design. An optimal integral criterion and an appropriate robust
measure for degradation of the system performances due to variation of the model are introduced in an
iterative mechanism. The theoretical approach presented in this paper is validated on a close loop control
system, the application being developed in simulation. The proposed strategy is aiming to implement
adaptive-robust control in practical process applications.
1 INTRODUCTION
The 1960-1980s became the most important period
for the development of control theory and in
particular adaptive control. System identification and
parameter estimation played a crucial role in the
reformulation and redesign of adaptive control
(Astrom & Wittenmark, 2008; Landau, 1995).
Adaptive control systems can automatically adjust
its parameters to compensate variations in the process
ensuring imposed performances even when the
system's dynamics change or uncertainties are
present. This adaptive system identifies in closed loop
parameters in real time, adapting the controller's
action to the applications where process parameters
are unknown or time-varying (Popescu & Gentil,
1998; Foulloy et al., 2004; Popescu et al., 2008).
As a difference from an adaptive control strategy,
in robust control rather than relying on real-time
adaptation to measured variations, the controller is
designed a priori to maintain performance under the
assumption that certain system parameters are
uncertain, but within known bounds.
The start of the theory of robust control took shape
in the 1980s and is still active today. The modern
theory of robust control system began in the late
1990s and soon developed a number of techniques for
dealing with bounded system uncertainty.
Robustness is the ability to keep imposed
performance unchanged under external disturbances
and uncertainties. Robust control is a technique
focused on ensuring a control system's performance
despite uncertainties in the process or its
environment. It aims to maintain imposed
performance even when faced with disturbances,
parameter or dynamic model structure variations.
Robust control is crucial for applications with
parameters and structure uncertainties, where
stability and reliability are essential.
2 CONTROL STRATEGIES
2.1 Adaptive Control
The evolution of systems theory during the 70s-80s
allowed the growth of interest and progress in
adaptive control strategies. The rapid development of
numerical computing resources, programming and
simulation facilities contributed to the emergence and
development of numerical methods for data
acquisition and processing, modelling and
Popescu, D., Dimon, C. and Borne, P.
An Adaptive-Robust Strategy Design for Process Control.
DOI: 10.5220/0013838900003982
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 517-523
ISBN: 978-989-758-770-2; ISSN: 2184-2809
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
517
identification of processes and design of control
algorithms. Under these favourable conditions, the
possibility of transferring the performance of control
systems obtained in simulation to real applications in
processes appeared. As a result, for real-time control,
adaptive strategies were recommended and
implemented in industrial process automation.
The adaptive control strategy proposes for each
sampling moment, a re-identification of the process
and a re-design of the control system. It ensures the
maintenance of nominal imposed performances on
the physical system that drives the process, at each
sampling moment.
The computational effort is significant and
demanding for processes with rapid evolution and
these limitations were cancelled by the robust control
strategy. The adaptive control mechanism is
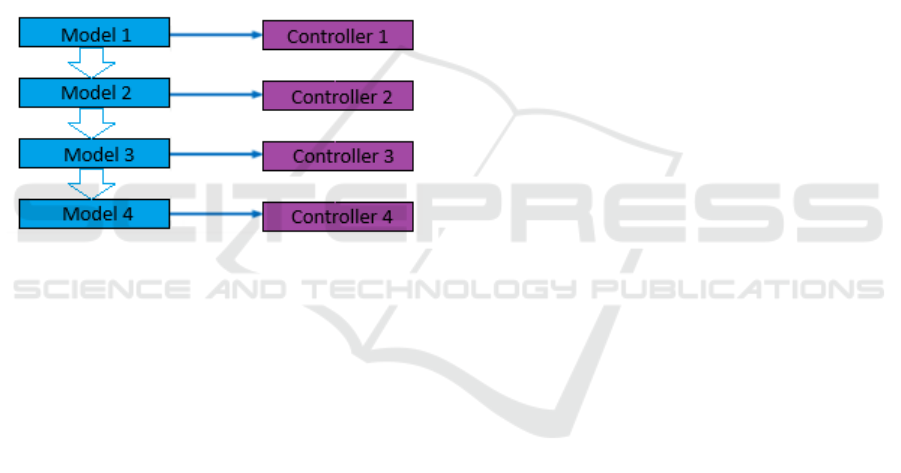
illustrated in Figure 1.
Figure 1: Adaptive control scheme.
The adaptive control mechanism is based on the
recursive relationship for repeated estimation of
model parameters and design of the control
algorithm, after the relation:
()( )
11
,,
kk k k
CM C M
++
→
(1
)
where
k
C
and
1k
C
+
are the controllers at step k and
k+1,
k
M
and
1k
M
+
are the models at step k and k+1.
Adaptive control remains a recommended
solution for processes with model parametric
uncertainty (invariant structure and variable
parameters) and for slowly variable processes
described by low-order models (Astrom, 1983;
Chalam, 1987; Anderson, et al., 1986).
Successes after the 1980s, however, were soon
followed by controversies over the practicality of
adaptive control concerning the computational effort
for the reidentification of model parameters and the
redesign of the controller in real-time closed loop
system. Thus, the robust control alternative began
(Ogata, 1990; Lewis et al., 2012; Wang et al., 2013;
Doelman et al., 2009).
2.2 Robust Control
Robust control is a field of automatic control theory,
recommended for preserving the stability and
performance of systems with parametric and/or
structural model uncertainty. Robust design methods
ensure a maximum uncertainty region through
robustness corrections, in order to attenuate the
effects of disturbances. The robust controller is
tolerant to the action of disturbances and to the
nonlinearities in the system for a collection of models
associated with different operating regimes of the
process (Dullerud & Paganini, 1999).
Duncan McFarlane and Keith Glover of
Cambridge University propose a design method for a
robust H-infinity loop-shaping system in the
frequency domain by minimizing the disturbance-
output sensitivity function (McFarlane & Glover,
1992). The optimal-robust controller guarantees that
the system ensures an invariance of the performance
under the action of disturbances.
An important approach for the design of robust
systems in input-output representation is presented in
(Popescu et al., 2017). Robustness indicators in the
frequency domain (robustness margin and
disturbance-output sensitivity function) are
introduced to evaluate the robustness of the system
and a design method based on the remarkable
properties of the disturbance-output sensitivity
function is proposed. The nominal control system is
adjusted so that the sensitivity function respects, in
the frequency domain, a template imposed by
successive calibration techniques.
From an application-oriented perspective, sliding
mode control (SMC), represents an emerging area
within robust control. Its inherent robustness to
uncertainties, combined with its relative design
simplicity, has led to its widespread adoption across
a range of practical applications (Bojan-Dragos et al.,
2024). Other areas of application concern power
control for renewable sources of energy (Ghalem et
al., 2018).
The robust control strategy is represented in
Figure 2 and remains recommended for models with
parametric and/or structural uncertainty and for
nonlinear process models. Robust control preserves
system stability of the system and tolerates model
uncertainties caused by the action of disturbances or
process nonlinearities. The robust controller
preserves system performance for a class of models
associated with possible process operating regimes
(Popescu et al., 2017; Green & Limebeer, 2012;
Popescu et al., 2008).
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
518
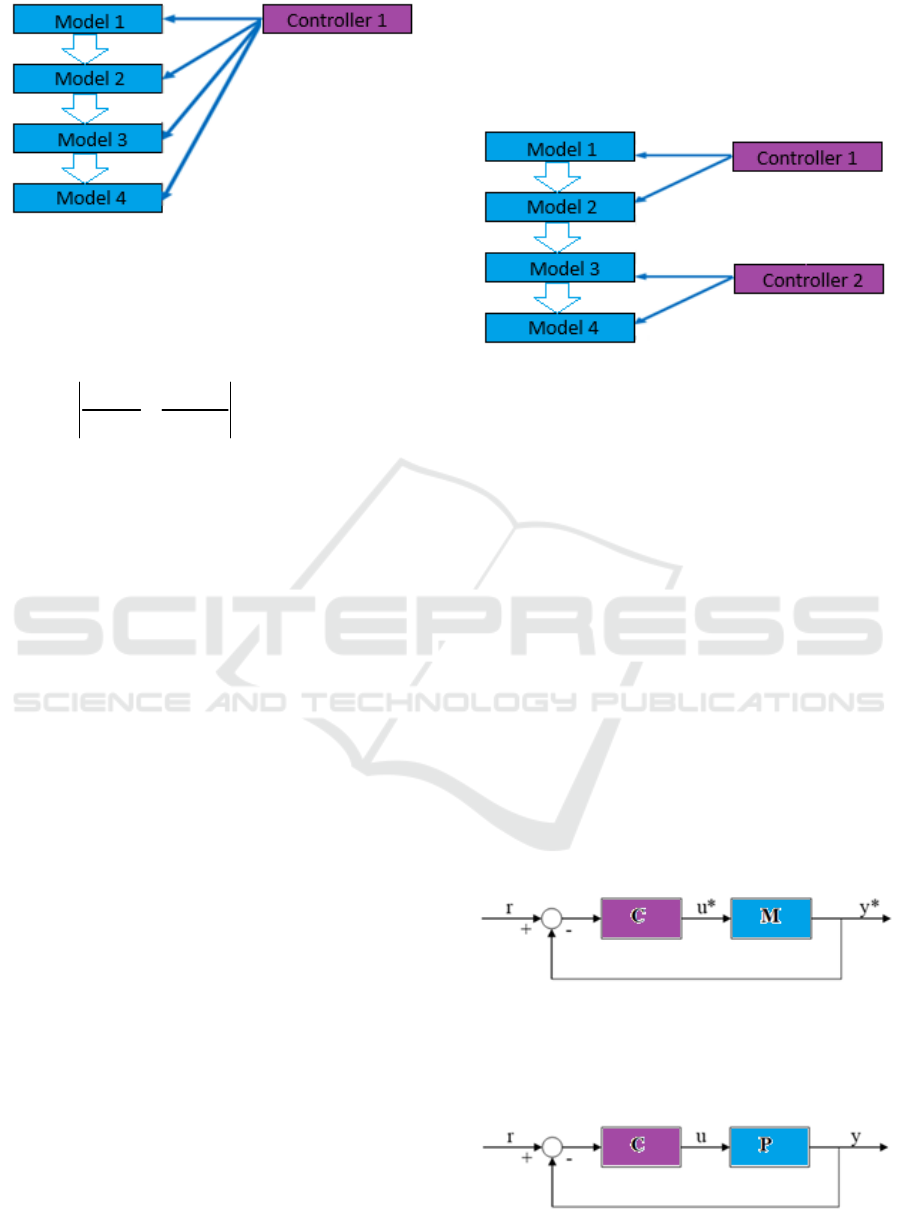
Figure 2: Robust control scheme.
The robustness reported to system performance is
expressed by relation (2), which expresses the
performance difference between the physical system
and the nominal system:
11
CP CM
s
mall
CP CM
−→
++
(2
)
where
C
is the controller computed for process
P
,
estimated by model
M
.
2.3 Adaptive-Robust Control
By the middle 1980s, several new redesigns and
modifications were proposed and recommended,
leading to a series of work known as robust adaptive
control.
The efficiency of integrated control systems in
automation solutions dedicated to technological
processes is determined by the process identification
and the system control design, two extremely
important concepts that ensure the performance of the
system. The behaviour of control systems in
industrial applications depends directly on the quality
of the mathematical model that expresses the process
dynamics and the control algorithm and therefore the
interdependence between the two concepts to ensure
the required performances is obvious. For a high level
of performance, the model must adapt when it
becomes uncertain for the process, and the control
algorithm must be tolerant to the action of
disturbances. Thus, starting with the 1990s, a new
concept was highlighted under the name of
identification for robust control, a concept that later
supported the adaptive-robust control strategy
(Athans et al., 2005; Ioannou & Sun, 2013; Narendra
& Annaswamy, 1986).
Important results on adaptive-robust control
strategies are obtained after 1990s and involved the
understanding of the various robust modifications and
their unification under a more general framework.
The adaptive–robust control strategy, proposed in this
paper, combines the advantages of adaptive control
and robust control respectively, by minimizing the
computational effort and by increasing the transfer of
simulation results in real time applications. This
strategy is shown in Figure 3.
Figure 3: Adaptive-robust control scheme.
3 ADAPTIVE-ROBUST
CONTROL METHODOLOGY
The main objective for this strategy is to combine
resources offered by adaptive and robust control in a
complementary manner to obtain high-performance
results in the automation of industrial processes.
The identification mechanism must be integrated
into an automatic control system and therefore a set
of models attached to the process dynamics must be
considered, if the nominal performances from the
simulation are to be maintained for the operation of
real processes. It is therefore proposed to perform an
identification and calculate a real-time command, for
the regulation of the process subjected to
disturbances.
Let us consider the nominal system (NS) with the
nominal performances (NP) validated in simulation,
represented in Figure 4:
Figure 4: Nominal control system (NS).
and the physical real system (RS) with performances
to be achieved (RP) on the physical process,
represented in Fig. 5:
Figure 5: Real control system (RS).
An Adaptive-Robust Strategy Design for Process Control
519

It is desired that the performances obtained in the
simulation are found as achieved performances, under
the conditions in which the process changes its
nominal operating point under the action of
disturbances.
In practice, the identification problem is solved by
minimizing the criterion constructed with the
estimation error and separately the optimal command
is calculated by minimizing another optimality
criterion depending on the regulation error system, as
follows:
• if a compensator
C
is known, the optimal
identification model
M
can be determined using an
identification criterion
I
J :
()
arg min ,
I
M
M
CM= J
(3
)
• if an identification model
M
is known, the
optimal compensator
C
can be determined using a
control criterion
C
J :
()
arg min ,
C
C
CCM= J
(4
)
The complementary relationship between the
problems of identification and control design is
supported by an iterative process (Gliga et al., 2008;
Levreetsky & Wise, 2024; Pham et al., 2025). The
two problems above can be defined in a unified
manner, which once again emphasizes the
complementarity between the two optimization
problems within the general problem of designing
automatic control systems.
Our approach is based on the idea that
identification should be carried out for the purpose of
control design and not separately. For this reason, a
single criterion remains important, for example
C
J
.
Given an optimization criterion
J
(for example,
J ≡ J
) and a corresponding norm, its optimal value
is obtained by minimizing
‖
J
‖
on the set of model-
compensator pairs associated with the process.
In practice, the compensator built from an
estimated model must lead to similar performances in
simulation and on the operating process. There are
thus two additional types of restrictions imposed by
the criterion
J
:
‖
J
𝐶, 𝑀
‖
< 𝛿
(5)
‖
J
𝐶, 𝑃
−J
𝐶, 𝑀
‖
≪
‖
J
𝐶, 𝑀
‖
(6)
where
δ
is the degradation error. The norms in the
above inequalities have natural interpretations, such
as:
•
‖
J
𝐶, 𝑀
‖
represents the nominal
performance;
•
‖
J
𝐶, 𝑃
‖
represents the performance
achieved during operation;
•
‖
J
𝐶, 𝑃
−J
𝐶, 𝑀
‖
measures the
degradation of the nominal performance, while the
compensator was built starting from the estimated
model
M
and not from the real model P .
Constraint (5) ensures good nominal
performance, while constraint (6) refers to
robustness. The value of
‖
J
𝐶, 𝑀
‖
being
sufficiently small, the performance degradation will
also be reduced.
We should also point out that this constraint does
not necessarily have to be verified if the nominal
performance
‖
J
𝐶, 𝑀
‖
is close to the realized
performance
‖
J
𝐶, 𝑃
‖
.
As this is difficult to test, the
robustness constraint (6) is imposed. If this is
verified, then the nominal and realized performances
are close.
The criterion
J
can be used to trigger an iterative
calculation process aiming to obtain a model-
compensator pair as close as possible to the optimal
pair. It is sufficient to use the performance
degradation measure for both the optimization and
identification criterion of the nominal performance
I
J
and for the optimization function in the
evaluation of the command
‖
J
‖
(Borne et al., 2013;
Stefanoiu et al., 2014).
The generic stage of this mecanism is described
below (for all
𝑖∈ℕ):
𝑀
= 𝑎𝑟𝑔𝑚𝑖𝑛
‖
J
𝐶
, 𝑃
−J
𝐶
, 𝑀
‖
𝐶
= 𝑎𝑟𝑔𝑚𝑖𝑛
‖
J
𝐶
, 𝑀
‖
(7
)
For each iterative step, the constraints (5) and (7)
must be verified, expressed in the form:
‖
J
𝐶
, 𝑀
‖
< 𝛿
(8)
‖
J
𝐶
, 𝑃
−J
𝐶
, 𝑀
‖
≪
‖
J
𝐶
, 𝑀
‖
(9)
Relations (7), (8) and (9) constitute the core of the
iterative process. The recursive algorithm is shown in
the diagram in Figure 6.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
520

Figure 6: Recursive adaptive-robust algorithm.
The recursive algorithm will stop while the
conditions (8) and (9) are verified, otherwise it goes
to the identification of the model, and the algorithm
starts again. The controller that satisfies condition (8)
is the robust adaptive controller implemented on the
real system structure (RS).
Let us consider:
2
min ( )
J
etdt=
(10)
the optimal integral criterrion for designing the
controller, where
()et is the control error of the
closed loop system.
The expression (10) becomes:
𝐽
= 𝑚𝑖𝑛
𝑒
(𝐶, 𝑀)𝑑𝑡
(11)
which accepts a direct representation of the criterion
as follows:
𝐽
= 𝑚𝑖𝑛
(
𝐶, 𝑀
)
(12)
For a fixed model
M
, identified from the
measure the robustness degradation, we can compute
the new controller:
𝐽
= 𝑚𝑖𝑛
(
𝐶
)
(13)
The main steps of the proposed algorithm are the
following:
- A closed-loop control system
(𝐶
, 𝑀
), which
ensures performance at a nominal operating point of
the process
0
P , is considered.
- If the perturbed process changes the operating
point
i
P driven by the system (𝐶
, 𝑀
) to the new
point
1i
P
+
, a new model
1i
M
+
is re-identified by
minimizing the performance degradation due to the
model parametric uncertainty.
- A new controller
𝐶
is recomputed using the
optimality criterion
J
.
- The recursive procedure ends if the performance
degradation becomes insignificant.
As mentioned earlier, the following optimal
integral criterion
J
is considered:
𝐽
=
𝑒
(𝑡)𝑑𝑡
∞
(14
)
After some mathematical transformations,
detailed in (Calin et al., 1979), the direct expression
of the integral criterion is obtained as follows:
2(1 )
ir
rr
TKk
J
Kk Kk
+τ
=
+
(15
)
The unique optimality criterion
J
is used to
identify the process model by minimizing the
degradation measure and respectively to recompute
the controller by minimizing the same criterion. After
estimating the new model, the new controller is
designed to preserve the system performance using
the relations (7). Thus, the limitations of the closed-
loop model adaptation strategy given by the redesign
of the control algorithm at each sampling moment are
reduced by the effect of the robust strategy.
4 STUDY-CASE AND
SIMULATIONS
A simple study case for understanding the adaptive-
robust approach is presented considering a first order
process model and a PI controller for the system. For
higher order systems, the design methodology
remains the same, just the number of mathematical
calculations increases with the order of the process
model and of the controller complexity.
Let us consider a process expressed using a first
order transfer function:
()
1
k
Ps
s
τ
=
+
(16
)
An Adaptive-Robust Strategy Design for Process Control
521
and the PI control algorithm which will be used for
the system:
1
() 1
r
i
Cs K
Ts
=+
(17)
Let us consider the process from (16) given by the
parameters
2k =
and
10τ=
. We can initialize the
controller by using a poles placement method,
considering as performances: zero overshoot and 40
sesonds response time. The computed controller is
given by the parameters
,0
0.5
r
K =
and
,0
10
i
T =
.
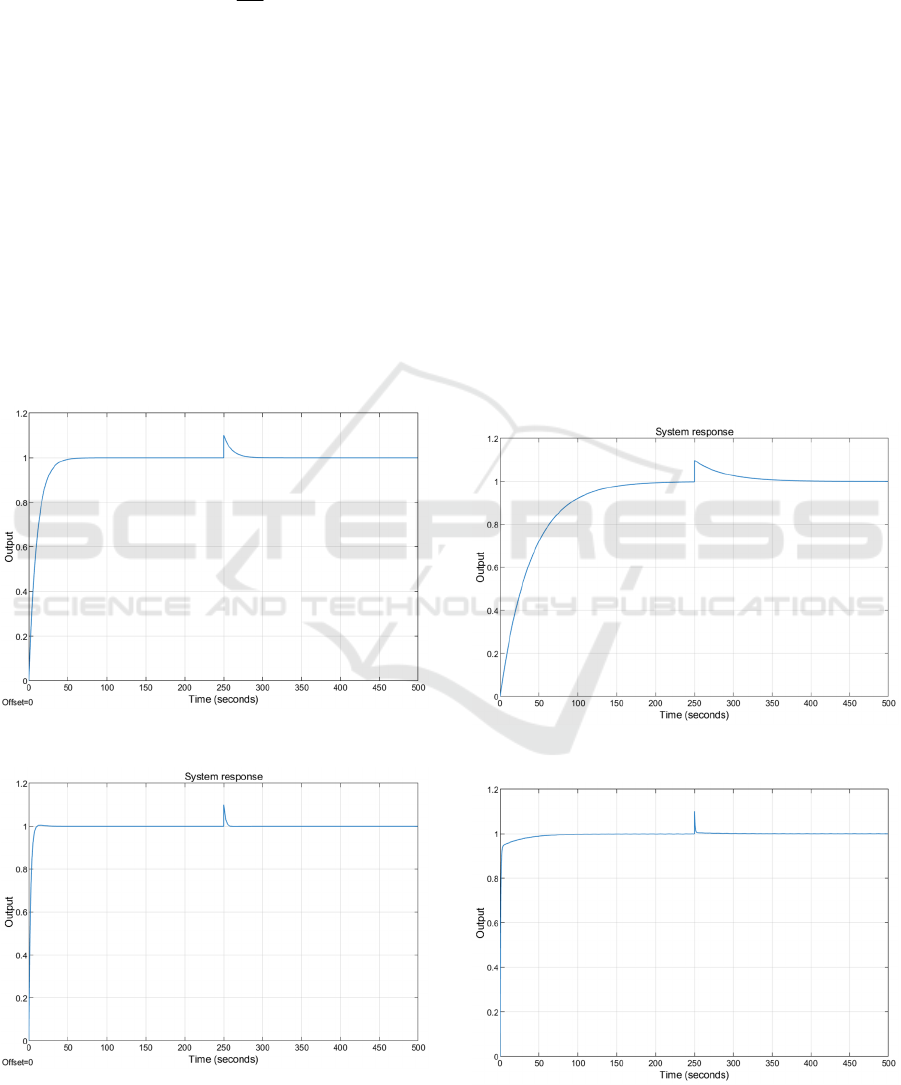
The system response is represented in Figure 7. A
10% disturbance is added to the output of the system
at time t=250s, which is rejected. It should be noted
that the computed controller will be maintained as
long as the degradation error criterion given by (8) is
verified. The degradation error in this case will be
𝛿 =J
(
𝐶
, 𝑀
)
=5.
Figure 7: System response for
(𝐶
, 𝑀
)
.
Figure 8: System response for
(𝐶
, 𝑀
)
.
By using the Cauchy gradient method with the
ceriterion function given by (15),
the algorithm will
compute a new controller only when necessary.
The optimum values for the controller at iteration i:
𝐾
,
*
= 10.592 and 𝑇
,
*
= 8.2574 . The degradation
error will be given by the new value
𝛿 =
J
(
𝐶
, 𝑀
)
= 1.0454
. The system response is shown
in Figure 8.
In time the model of the process will change, such
that the controller will not be able to assure the
nominal performances. Such a case is represented in
Figure 9, where the process is identified by a new
model
1i
M
+
. By applying the same principle, we
obtained the controller
1i
C
+
and the system response
is represented in Figure 10. The degradation error is
given by
𝛿 =J
(
𝐶
, 𝑀
)
= 0.3885
.
It can be noticed that the system performances are
verified; in fact, we obtained better response time
compared with the initial response (the response time
is about 33 seconds).
Figure 9: System response for
(𝐶
, 𝑀
)
.
Figure 10: System response for
(𝐶
, 𝑀
)
.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
522

5 CONCLUSIONS
The paper proposes a new adaptive-robust control
strategy for the development of industrial automation
applications.
The main objective for this strategy is to combine
the advantages offered by adaptive and robust control
in a complementary manner to obtain high-
performance results in the automation of
technological processes with parametric and/or
structural uncertainties.
Adaptive-robust control is recommended for
processes with parametric and/or structural
uncertainty, tolerant to the action of disturbances and
nonlinearities in the process.
Adaptive-robust control is based on the concept of
robust degradation measure and uses a recursive
calculation procedure, by using a single optimality
criterion that minimizes the degradation measure for
the identification operation, and which calculates the
optimal command.
The theoretical results validated in simulation can
be transferred as efficient solutions for the automation
of real technological processes and installations
guaranteeing superior performances in operation.
REFERENCES
Anderson, B.D.O., Bitmead, R.R., Johnson, C.R.,
Kokotovic, P.V., Kosut, R.L., Mareels, I., Praly, L.,
Riedle, B. (1986). Stability of Adaptive Systems, M.I.T.
Press, Cambridge, Massachusetts.
Astrom, K.J. (1983). Theory and applications of adaptive
control - a survey, In Automatica, vol.19, no.5, pp. 471-
486.
Astrom, K.J., Wittenmark, B. (2008). Adaptive Control,
Courier Corporation.
Athans, M., Fekri S., Pascoal, A. (2005). Issues on robust
adaptive feedback control. In Preprints of the 16th
IFAC World Congress, pp. 9-39.
Bojan-Dragos, C.A., Precup, R.E., Petriu, E., Tibre, R.A.,
Han, T. (2024). Sliding Mode and Super-Twisting
Sliding Mode Control Structures for Vertical Three-
Tank Systems. In Studies in Informatics and Control
Journal, Vol. 33, No. 3, 2024.
Borne, P., Popescu, D., Filip F.G., Stefanoiu, D. (2013).
Optimization in Engineering Sciences- Exact Methods,
J.Wiley Press, London.
Calin, S., Tertisco, M., Dumitrache, I., Popeea, C., Popescu,
D. (1979). Optimizations in industrial automation,
Tehnica Press, Bucharest.
Chalam, V. V. (1987). Adaptive Control Systems:
Techniques and Applications, New York.
Doelman, N., Fraanje, R., Houtzager, I., Verhaegen, M.
(2009). Adaptive and real-time optimal control for
adaptive optics systems. In ECC-European Control
Conference, Proceedings.
Dullerud. G.E., Paganini, F. (1999). A Course in Robust
Control, Springer-Verlag, Berlin.
Foulloy, L., Popescu, D., Dauphin-Tanguy, G. (2004).
Modelisation, Identification et Commande des
Systemes, Romanian Academy Press, Bucharest.
Ge, S.S., Wang, C., Li, Y., Lee, T.H., Ang, M.H. (2013).
Adaptive optimal control for linear discrete time-
varying systems. In IEEE Conference on Cybernetics
and Intelligent Systems, Proceedings.
Ghalem, A., Tayeb A., Attallah, S., Abdeldjabbar, K.M.
(2018). Robust and modern control of VSC-HVDC. In
U.P.B. Sci. Bull., Series C, vol. 80(2).
Gliga, L., Cosmin, M., Lupu, C., Popescu, D. (2008).
Adaptive–Robust Control, a computational efficient
real time simulation. In EMES International
Conference, Oradea.
Green, M., Limebeer, D.J.N. (2012). Linear Robust
Control, Courier Corporation.
Ioannou, V.P., Sun, J. (2013). Robust Adaptive Control,
Courier Corporation.
Landau, I.D. (1995). Identification et Commande des
Systemes, Hermes Publishing, Paris.
Levreetsky, E., Wise, K. (2024). Robust and Adaptive
Control: With Aerospace Applications (Advanced
Textbooks in Control and Signal Processing),
SpringerPress.
Lewis, F.L., Vrabie, D., Syrmos, V.L. (2012). Optimal
Control, John Wiley and Sons.
McFarlane, D., Glover, K. (1992). A loop-shaping design
procedure using H/sub infinity / synthesis. In IEEE
Transactions on Automatic Control, vol. 37, no. 6, pp.
759-769.
Narendra, K.S., Annaswamy, A.M. (1986). Robust
Adaptive Control in the Presence of Bounded
Disturbances. In IEEE Transactions on Automatic
Control, vol. 31, no. 4, pp. 306-315.
Ogata, K. (1990). Modern Control Engineering, Practice
Hall, New Jersey.
Pham, D.A., Han, S.H., Kong, K.J. (2025). Time-Specified
Adaptive Robust Control Framework for Managing
Nonlinear System Uncertainties. In Appl.Sci., 16(6).
Popescu, D., Gentil, S. (1998). Commande Numerique et
Intelligence Artificielle en Automatique, Tehnica Press,
Bucharest.
Popescu, D., Stefanoiu, D., Lupu, C., Petrescu, C.,
Ciubotaru, B., Dimon, C. (2008). Industrial
Automation, Agir Press, Bucharest.
Popescu, D., Stefanoiu D., Borne, P. (2017). Process
Control Design for Industrial Applications, John Wiley
Press, London.
Stefanoiu, D., Borne, P., Popescu, D., Filip, F.G. (2014).
Optimization in Engineering Sciences- Metaheuristic,
Stochastic Methods and Decision Support, J.Wiley
Press, London.
An Adaptive-Robust Strategy Design for Process Control
523
