Combining off-Policy and on-Policy Reinforcement Learning for

Dynamic Control of Nonlinear Systems

Hani Hazza A. Ahmed

, Simon G. Fabri

, Marvin K. Bugeja

and Kenneth. Camilleri

Department of Systems and Control Engineering, University of Malta, Msida, Malta

Keywords: Control Systems, Q-Learning, SARSA, QARSA, Reinforcement Learning, Nonlinear, Cart Pole, AI,

Rewards, on-Policy, off-Policy, Python.

Abstract: This paper introduces QARSA, a novel reinforcement learning algorithm that combines the strengths of off-

policy and on-policy methods, specifically Q-learning and SARSA, for the dynamic control of nonlinear

systems. Designed to leverage the sample efficiency of off-policy learning while preserving the stability and

lower variance of on-policy approaches, QARSA aims to offer a balanced and robust learning framework.

The algorithm is evaluated on the CartPole-v1 simulation environment using the OpenAI Gym framework,

with performance compared against standalone Q-learning and SARSA implementations. The comparison is

based on three critical metrics: average reward, stability, and sample efficiency. Experimental results

demonstrate that QARSA outperforms both Q-learning and SARSA, achieving higher average rewards,

stability, sample efficiency, and improved consistency in learned policies. These results demonstrate

QARSA’s effectiveness in environments were maximizing long-term performance while maintaining learning

stability is crucial. The study provides valuable insights for the design of hybrid reinforcement learning

algorithms for continuous control tasks.

1 INTRODUCTION

Reinforcement Learning (RL) has become a

prominent approach in developing intelligent agents

capable of learning optimal behaviors through

interactions with their environment. Central to this

paradigm is the reward signal, which the agents aim

to maximize over time. The flexibility and

effectiveness of RL have made it widely applicable

across diverse domains such as robotics and game

playing, cementing its importance in artificial

intelligence research (AlMahamid & Grolinger,

2022).

Among various RL methodologies, temporal

difference (TD) learning stands out for its capacity to

learn from direct interactions without explicit

environmental models.

This paper introduces a novel reinforcement

learning algorithm, QARSA, combining off-policy

and on-policy learning approaches, specifically Q-

https://orcid.org/0009-0006-1466-2138

https://orcid.org/0000-0002-6546-4362

https://orcid.org/0000-0001-6632-2369

https://orcid.org/0000-0003-0436-6408

learning and SARSA. Off-policy methods like Q-

learning emphasize past experiences, enhancing the

accumulation of rewards, sample efficiency, and

facilitating rapid learning. Conversely, on-policy

methods such as SARSA directly utilize the current

policy in their updates, resulting in greater stability

and lower variance. By merging these complementary

features, QARSA, the novel algorithm proposed in

this work, aims to achieve improved rewards and

sample efficiency alongside increased stability.This

is particularly suitable for dynamic control scenarios

involving nonlinear systems.

To evaluate the effectiveness of QARSA, this

work applies the algorithm to the classical cart-pole

problem, a well-established benchmark for assessing

RL performance in control tasks. The cart-pole

environment requires the agent to balance a pole

upright on a moving cart by applying directional

forces, exemplifying the critical balance between

Hani Hazza, A. A., Fabri, S. G., Bugeja, M. K. and Camilleri, K.

Combining off-Policy and on-Policy Reinforcement Learning for Dynamic Control of Nonlinear Systems.

DOI: 10.5220/0013836700003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 387-394

ISBN: 978-989-758-770-2; ISSN: 2184-2809

387

exploration and exploitation required for successful

control (Surriani et al., 2021).

Therefore, this paper aims to analyze and compare

the performance of QARSA, Q-learning, and SARSA

on the cart-pole problem. This comparison will

provide valuable insights into the relative strengths

and limitations of each algorithm. Additionally, this

paper analyzes the learning curves, final outcomes,

hyperparameter sensitivity, and the impact of various

function approximation techniques. Through this

comprehensive analysis, the strengths and

weaknesses of the new QARSA algorithm are

highlighted, contributing valuable insights into its

practical applicability and scalability in

reinforcement learning for control tasks.

2 BACKGROUND WORK

Two of the most fundamental model-free methods in

RL are Q-Learning and SARSA. Both fall under the

category of Temporal-Difference (TD) learning, and

update a value function based on the agent's

experience without requiring a model of the

environment.

Sutton & Barto, (2018) highlighted that SARSA's

conservative update mechanism can yield superior

performance in environments where cautious

exploration strategies are beneficial. Double Q-

learning (Van Hasselt et al., 2016) and Weighted Q-

learning (Cini et al., 2020) address the overestimation

bias inherent in traditional Q-learning, leading to

enhanced stability and improved outcomes,

particularly in environments characterized by high

complexity and variability in action-value functions.

Several comparative analyses have investigated how

RL algorithm performance can be influenced by

exploration methods (e.g., ε-greedy, softmax), reward

shaping, and discretization strategies such as those by

Tokic (2010). These elements are particularly critical

in continuous-state environments like the cart-pole

task, which require discretization for tabular RL

methods.

Nagendra et al. (2017) and Zhong (2024)

conducted comparisons of various RL algorithms,

emphasizing sample efficiency and stability.

However, a thorough comparative analysis explicitly

evaluating Q-learning and SARSA based on

cumulative rewards per episode in this environment

remains under-explored. Mothanna & Hewahi (2022)

demonstrated the applicability of Q-learning and

SARSA in solving the cart-pole problem, proposing

future work to extend the analysis to additional RL

algorithms.

Despite these developments, limited direct

comparative work specifically addresses the learning

efficiency, stability, and ultimate performance of Q-

learning and SARSA in the cart-pole environment.

Most existing comparative studies have either

examined more complex tasks or employed different

evaluation metrics. Those works that focus on the

cart-pole problem utilize the OpenAI Gym simulation

framework and include metrics such as average

reward, stability, sample efficiency, and overall

effectiveness (Brockman et al., 2016).

In (Hazza et al.,2025) the performances of three

reinforcement learning algorithms were collectively

compared under a sensitivity analysis in which all

hyperparameter values were systematically varied to

observe their impact on the learning process. While

Q-learning exhibited marginally higher average and

cumulative rewards, the differences among

Q-learning, SARSA, and Double Q-learning were not

substantial across the tested range, indicating that no

single method decisively outperforms the others.

Q-Learning and SARSA represent two

fundamentally different approaches to value-based

learning (Kommey et al., 2024) . Q-Learning is an

off-policy algorithm that learns the value of the

optimal policy independently of the agent's actions.

While effective in many deterministic environments,

its reliance on the maximum Q-value in the update

step can lead to overestimation bias and instability in

noisy or stochastic environments. In contrast, SARSA

is an on-policy method that learns the value of the

policy the agent is actually following. It tends to be

more stable and risk-averse, especially in

unpredictable environments, but often converges

more slowly and may be overly conservative (Wang

et al., 2013).

With this in mind, this work proposes a novel

hybrid approach, designed to merge the strengths of

on-policy and off-policy reinforcement learning

methods, and tested by simulation on the cart-pole

problem, as detailed in the rest of the paper.

2.1 Q-Learning Algorithm

Q-learning is one of the most widely used RL

algorithms, renowned for its simplicity and

effectiveness, introduced by Watkins in 1989

(Watkins & Dayan, 1992). It is an off-policy

algorithm that estimates the optimal action-value

function Q (s, a) by learning from the maximum

future reward, regardless of the agent's current policy.

Its update rule is defined by Equation (1):

Q (s, a) ← Q (s, a) + α [r + γ max_a′ Q (s′, a′) −

Q (s,a)] (1)

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

388

Here, Q (s, a) denotes the Q-value of taking action a

in state s, α is the learning rate, γ is the discount factor,

r is the immediate reward, and s′ is the next state after

action a, and a′ is the action taken in the next state s′.

The use of the maximum Q-value over next actions a′

makes Q-Learning optimistic and efficient in

deterministic settings, but it can suffer from

overestimation in noisy environments.

2.2 SARSA Algorithm

SARSA (State-Action-Reward-State-Action) refers

to an on-policy method that updates the value

function based on the actual actions taken by the

agent under its current policy (Sutton & Barto, 2018).

The SARSA update rule is given by Equation (2):

Q (s, a) ← Q (s, a) + α [r + γ Q (s′, a′) −

Q (s,a)] (2)

In this case, a′ is the next action actually chosen

by the policy, not necessarily the one with the

maximum value. This makes SARSA more

conservative and safer in stochastic environments, as

it learns the action-values according to the policy

being followed.

Previous studies, such as those by Singh and

Sutton (1996), have compared these two algorithms

under various conditions. SARSA tends to perform

better in environments with high variability or where

risk-averse behavior is preferred, while Q-Learning

often converges faster in deterministic tasks.

2.3 QARSA: A Hybrid Reinforcement

Learning Algorithm

Recognizing the complementary strengths and

weaknesses of Q-Learning and SARSA algorithms,

we propose QARSA (a hybrid of the two). This

algorithm combines the update rules of both Q-

Learning and SARSA via a tunable blending

parameter λ ∈ [0,1].

By adjusting λ, QARSA can strike a balance

between the aggressive, policy-independent updates

of Q-Learning and the cautious, policy-aware updates

of SARSA. This makes it particularly suited for

environments that exhibit both deterministic and

stochastic behaviors. We evaluate QARSA against its

parent algorithms to assess performance differences

using simulation experiments in a the cart-pole

control environment.

2.3.1 QARSA Update Rule

The QARSA update rule is given by Equation (3):

(

s, a

)

←Q

(

s, a

)

+αr+γλmax





(



)

(

1−λ

)

(



)

−Q

(

s, a

)

 (3)

where s is the current state, a is the current action, r is

the reward, s′ is the next state, a′ is the action taken in

state s′ (based on policy), α is the learning rate, γ is

the discount factor, and λ is the blending factor,

controlling the mix between Q-Learning and SARSA.

This update rule allows for a weighted

combination between on-policy and off-policy

learning.

By adjusting λ, the agent can adopt a learning

style that is best suited to the environment's

characteristics.

2.3.2 Behaviour and Interpretation

When λ→1: QARSA is equivalent to Q-Learning,

using the maximum expected return for future

actions. This can speed up learning but risks

overestimating the value function in stochastic

environments.

When λ→0: QARSA reduces to SARSA, basing the

value update on the actual action taken. This often

results in safer but slower learning.

Intermediate λ: Provides a balance; the agent is

neither too optimistic nor too cautious, which can lead

to improved stability and better generalization.

3 METHODOLOGY

3.1 Environment Setup

The cart-pole problem is a well-known benchmark in

the use of reinforcement learning for control systems.

It is favoured for its straightforward design and fast

training time. However, its simplicity also limits its

applicability, meaning that insights gained from this

task may not extend well to more complex scenarios,

particularly those that involve continuous action

spaces or high-dimensional visual inputs. The RL

model for this setup is shown in Figure 1. In this task,

the agent’s goal is to keep the pole balanced in the

inverted position by applying forces to move the cart

either left or right. The following considerations are

to be noted:

Combining off-Policy and on-Policy Reinforcement Learning for Dynamic Control of Nonlinear Systems

389

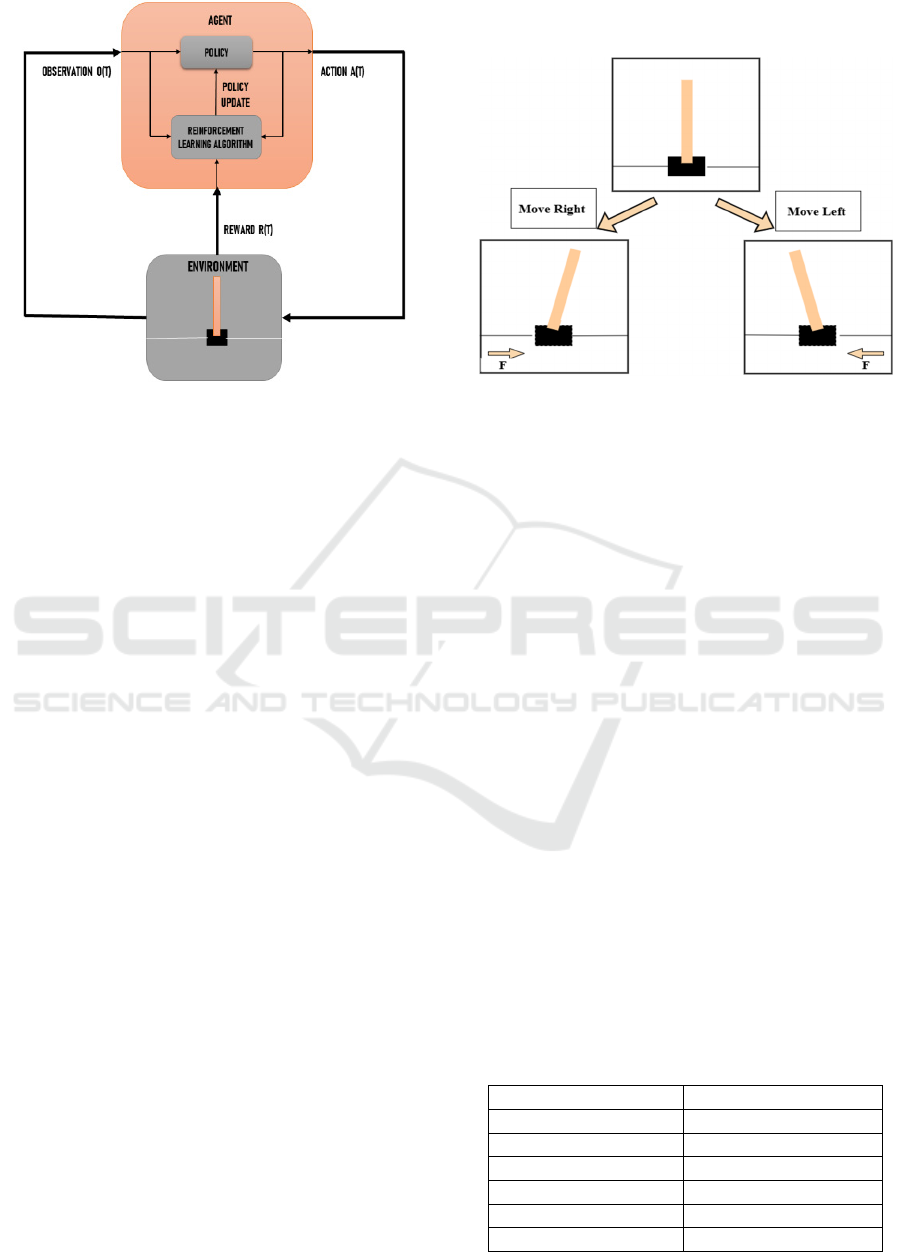
Figure 1: The Reinforcement Learning Model for The Cart

Pole Problem.

• State Space: This consists of the system's

state variables that describe the system’s

dynamics.

The state space consists of four continuous

parameters: The cart position (x), which can vary

within the range of -2.4 to +2.4 meters, the pole angle

(θ) that in this set-up will range from -0.2095 to

+0.2095 radians (equivalent to -12° to +12 °), the cart

velocity (ẋ), and the pole angular velocity ((𝜃) ). The

last two are unbounded and can take any value

(Mishra & Arora, 2023).

• Action Space: The action space is discrete

and consists of two possible moves:

0: Apply force to push the cart to the left, and

1: Apply force to push the cart to the right.

The resulting state depends on the action taken. For

example, as illustrated in Figure 2, if the system starts

with the pole in an upright position and the cart is

pushed to the left, the pole typically leans to the right,

leading to a new state, and vice versa.

• Reward Structure: The agent earns a

reward of +1 for every time step that the pole

angle remains within the ± 12° angle range.

If the pole tilts beyond ±12 degrees or when the cart

position exceeds the horizontal boundary of ±2.4m

from the centre, that specific episode of the simulation

is stopped. An episode is also stopped if the pendulum

angle and position remain within the prescribed ranges

for up to 500 time steps, corresponding to 10 seconds

of simulated time, with each step representing 20

milliseconds, this being considered as constituting

successful balancing control for a significant amount

of time (Li et al., 2024).

Figure 2: Typical Actions Performed by The Cart Pole

Problem.

3.2 Algorithm Implementation

As this study aims to implement and compare the

Q-learning, SARSA, and QARSA algorithms, they

were developed using the same core parameters to

ensure a fair and consistent evaluation. Q-learning is

implemented using a tabular approach, where the

action-value function Q (s, a) is stored in a table and

updated using the Bellman Equation 1. Similarly,

SARSA is applied as a tabular method, but its Q-

value updates incorporate the action taken in the next

state, following the SARSA update rule in Equation

2. QARSA combines elements of both Q-learning and

SARSA, as described in Section 2.3.

Table 1 presents the hyperparameter values

identified through experimental trials as having the

most significant influence on the algorithms’

performance (Jumaah et al., 2025). These parameter

values were chosen based on established practices in

the literature and were fine-tuned to enhance the

overall performance of all three algorithms. The

second column of Table 1 displays the optimized

values found by experimentation to yield the best

results.

Table 1: Hyperparameter values of Q-Learning, SARSA,

and QARSA algorithms for the Cart Pole Problem.

Hyperparameter Value

Learning Rate α 0.09

Discount Factor γ 0.07

Blending factor λ 0.5

Exploration Strategy ϵ 0.995

Number of Episodes 5000

Max Steps per Episode 500

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

390

3.3 Experimental Procedure

The experimental process was structured as follows:

Each algorithm began by initializing the Q-table(s) to

zero for all state-action pairs. Training commenced

by resetting the CartPole-V1 environment to initialize

the starting state for each episode. Actions were

selected using the epsilon-greedy policy, primarily

choosing the action with the highest estimated

reward. The selected action was executed, after which

the environment's reward and next state were

observed. Subsequently, the Q-value(s) were updated

according to the algorithm-specific update rule. If an

episode concluded due to the pole falling or the cart

moving out of bounds, the total accumulated reward

for that episode was recorded.

3.4 Performance Metrics

The following metrics were employed to assess the

algorithm performance (Escobar et al., 2020):

• Average Reward: Calculated as the mean total

reward received per episode throughout the

training period, serving as a primary indicator of

algorithm efficacy.

• Stability: This metric assesses the consistency

of algorithm performance once convergence is

achieved. Stability was quantified by calculating

the standard deviation of rewards over the final

100 episodes, with lower values indicating

higher stability and consistent behavior.

• Sample Efficiency: This evaluates how

effectively an algorithm improves its

performance given limited experiences.

Specifically, sample efficiency was measured

by the cumulative reward obtained over the first

1000 episodes, reflecting how rapidly each

algorithm learns an effective policy.

3.5 Computational Issues

All algorithms and simulations were implemented

using Python 3.10 with the following essential

libraries: the OpenAI Gym: CartPole-v1

environment, NumPy for numerical computation, and

Matplotlib for visualization and plotting of learning

curves. Experiments were executed on a standard

computer equipped with a 12th Gen Intel(R) Core

(TM) i9-12900K 3.20 GHz processor, 32.0 GB RAM,

and NVIDIA® GeForce RTX™ 4090 GPU to run the

simulations in a reasonable time.

Evaluation becomes computationally expensive

due to the rapid growth of the state and action spaces

as discretization increases. For instance, discretizing

the state variables cart position, cart velocity, pole

angle, and pole angular velocity into fixed intervals

significantly expands the size of the state-action

space, leading to increased computational overhead

and complexity in learning and decision-making

possible state-action (Tallec et al., 2019). As a result,

the Q-table grows exponentially with finer

discretization, significantly increasing memory

requirements and the computational overhead for

value updates during training. Moreover, each

simulation involves frequent table lookups, policy

evaluations, and Q-value updates, all of which scale

with the size of the discretized space.

This necessitates high-performance

computational resources, especially when running

repeated trials across multiple algorithms to study the

statistical significance of the results in comparative

analyses (Gogineni et al., 2024).

4 RESULTS AND DISCUSSION

The performance of the Q-learning, SARSA, and

QARSA reinforcement learning algorithms was

assessed using the previously described metrics

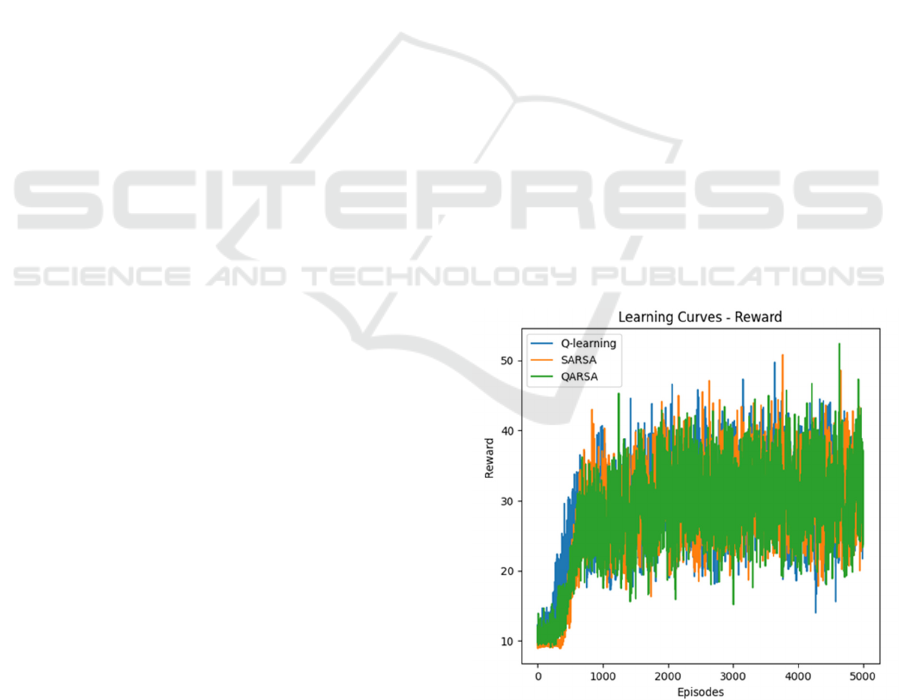
across 5,000 episodes. The first results are illustrated

in the learning curves shown in Figure 3. All three

algorithms demonstrate rapid progress during the first

1,000 episodes, suggesting fast initial learning, but

also display significant variability in their

performance.

Figure 3: Reward Performance of Q-Learning, SARSA, and

QARSA Algorithms for The Cart Pole Problem.

This pattern may reflect the agent’s exploration of

various strategies or challenges in consistently

Combining off-Policy and on-Policy Reinforcement Learning for Dynamic Control of Nonlinear Systems

391

maximizing rewards, potentially due to a non-

stationary or highly stochastic environment.

The frequent intersections of the learning curves

further support the notion that the algorithms perform

comparably overall, with no single method clearly

outperforming the others throughout all episodes.

This observation is consistent with the average

reward results that highlight QARSA's slight

advantage in overall performance, as illustrated in

Figure 4.

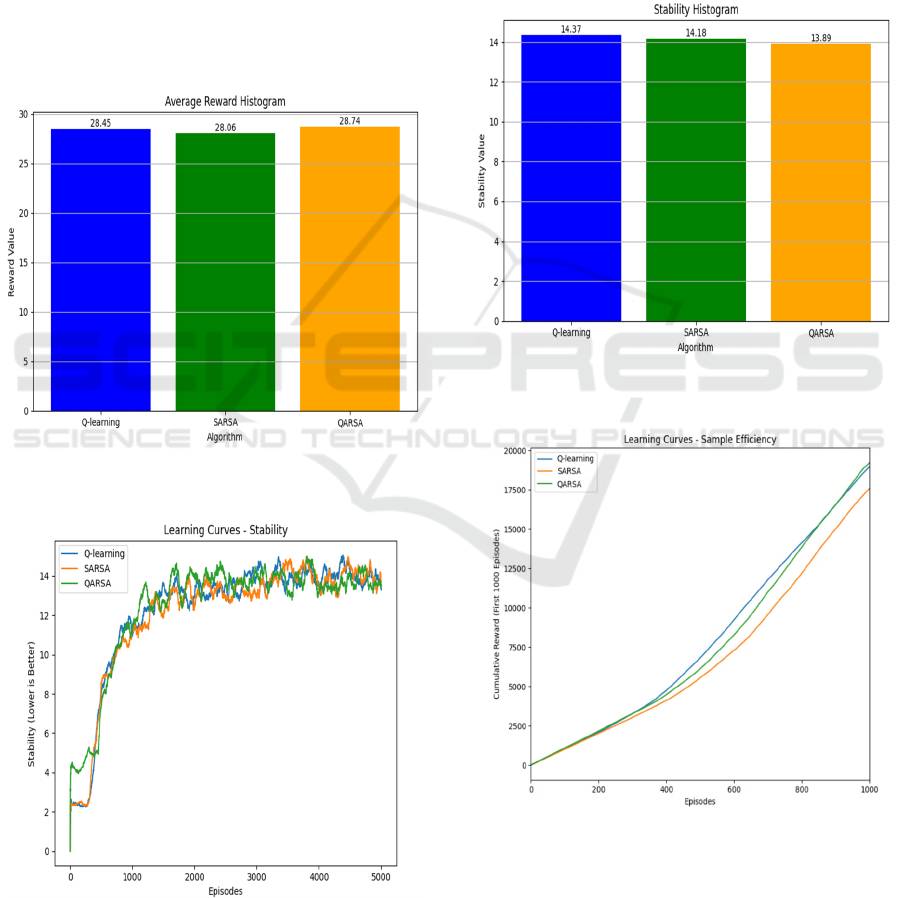
QARSA attained the highest average reward

(28.74) with a total of 143712.4 rewards, followed

closely by Q-learning average reward (28.45) with a

total of 142264.9 rewards, and then SARSA average

reward (28.06) with a total of 140319.2 rewards.

Figure 4: The Average Reward of Q-Learning, SARSA, and

QARSA Algorithms for The Cart Pole Problem.

Figure 5: Stability Performance of Q-Learning, SARSA,

and QARSA Algorithms for The Cart Pole Problem.

The slight differences in average rewards suggest

that all three algorithms performed similarly

regarding overall effectiveness. However, QARSA's

slightly higher average reward indicates it may have

a marginal advantage in maximizing long-term

returns.

The stability metrics for all three algorithms were

also comparable, with SARSA showing slightly

better stability (14.18) compared to Q-learning

(14.37) and QARSA showing the best stability

(13.89), as shown in Figures 5 and 6.

Figure 6: Stability of Q-Learning, SARSA, and QARSA

Algorithms for The Cart Pole Problem.

Figure 7: Sample Efficiency Performance of Q-Learning,

SARSA, and QARSA Algorithms for The Cart Pole

Problem.

As shown in Figures 7 and 8, QARSA demonstrated

the best sample efficiency (19212), followed by Q-

learning (18964.4) and SARSA (17585.2). QARSA

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

392

may learn more effectively from fewer experiences,

potentially making it more suitable for environments

where data collection is costly or limited.

Figure 8: The Sample Efficiency of Q-Learning, SARSA,

and QARSA Algorithms for The Cart Pole Problem.

Table 2 summarizes the final metrics obtained in the

three algorithms for the Cart Pole Problem, where the

best results are highlighted in grey.

Table 2: The Performance Comparison of Q-Learning,

SARSA, and QARSA for The Cart Pole Problem.

Metrics Q-Learning SARSA QARSA

Total

Rewards

142264.9 140319.2 143712.4

Average

Reward

28.45 28.06

28.74

Stability 14.37 14.18 13.89

Sample

Efficiency

18964.4 17585.2

19212

4 CONCLUSIONS AND FUTURE

WORK

This paper proposed QARSA, a novel reinforcement

learning algorithm that integrates off-policy and on-

policy learning principles by combining Q-learning

and SARSA. QARSA was evaluated in the CartPole-

v1 environment and compared against its constituent

algorithms. Simulation results demonstrated that for

the cart-pole problem, QARSA marginally

outperformed both Q-learning and SARSA across all

key performance metrics, achieving higher average

rewards, greater stability, and higher sample

efficiency. These results suggest investigating further

the performance of the proposed QARSA hybrid

reinforcement learning method for dynamic control

settings. Future work will thus focus on testing

QARSA in other complex environments, not only the

cart-pole problem, to investigate its scalability to

continuous state and action spaces, and explore

methods for determining the optimal value of the

blending factor between Q-learning and SARSA,

which is possibly dependent on the characteristics of

the system being controlled and the desired control

tasks. Finally, we will rigorously investigate the

comparative performance between the three

algorithms through Monte Carlo analysis and

statistical significance tests. Each algorithm has its

strengths, and literature shows that the choice of

optimal hyperparameters depends on the scenario

defining the problem and the specific requirements of

the task at hand (Manglik & Tripathi, 2018).

ACKNOWLEDGEMENTS

Research supported by project: “Setting up of a

transdisciplinary research and knowledge exchange

(TRAKE) complex at the University of

Malta (ERDF.01.124)” co-financed through the

European Union's European Regional Development

Fund 2014–2020.

REFERENCES

AlMahamid, F., & Grolinger, K. (2021). Reinforcement

Learning Algorithms: An Overview and Classification.

2021 IEEE Canadian Conference on Electrical and

Computer Engineering (CCECE), 2021, pp. 1-7

Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,

Schulman, J., Tang, J., & Zaremba, W. (2016). OpenAI

Gym. arXiv.org. https://arxiv.org/abs/1606.01540.

Cini, A., D'Eramo, C., Peters, J., & Alippi, C. (2020). Deep

reinforcement learning with weighted Q-

Learning. arXiv preprint arXiv:2003.09280.

Escobar, C. A. M., Pappalardo, C. M., & Guida, D. (2020).

A parametric study of a deep reinforcement learning

control system applied to the swing-up problem of the

cart-pole. Applied Sciences Switzerland, 10(24), 1–19.

Gogineni, K., Dayapule, S. S., Gomez-Luna, J., Gogineni,

K., Wei, P., Lan, T., Sadrosadati, M., Mutlu, O., &

Venkataramani, G. (2024). SwiftRL: Towards Efficient

Reinforcement Learning on Real Processing-In-

Memory Systems. ISPASS 2024, 217–229.

Hazza, H., Ahmed, A., Fabri, S. G., Bugeja, M. K., &

Camilleri, K. (2025). Reinforcement Learning Control

Strategies: Q-learning, SARSA, and Double Q-

learning Performance for the Cart-Pole Problem.2025

Combining off-Policy and on-Policy Reinforcement Learning for Dynamic Control of Nonlinear Systems

393

International Conference on Control, Automation and

Diagnosis (ICCAD), pp.1-6, 2025.

Jumaah, M. A., Ali, Y. H., & Rashid, T. A. (2025). Efficient

Q-learning hyperparameter tuning using FOX

optimization algorithm. Results in Engineering, 25.

Kommey, B., Isaac, O. J., Tamakloe, E., & Opoku, D.

(2024). A Reinforcement Learning Review: Past Acts,

Present Facts and Future Prospects. Journal Research

and Development (ITJRD), 8(2).

Li, P., Hao, J., Tang, H., Fu, X., Zhen, Y., & Tang, K.

(2024). Bridging evolutionary algorithms and

reinforcement learning: A comprehensive survey on

hybrid algorithms. IEEE Transactions on evolutionary

computation.

Manglik, A., & Tripathi, S. (2018). Towards integrating

model dynamics for sample efficient reinforcement

learning. Deep Reinforcement Learning (16-720)

Project.

Mishra, S., & Arora, A. (2023). A Huber reward function-

driven deep reinforcement learning solution for cart-

pole balancing problem. Neural Computing and

Applications, 35(23), 16705–16722.

Mothanna, Y., & Hewahi, N. (2022). Review on

Reinforcement Learning in CartPole Game. 2022

International Conference on Innovation and

Intelligence for Informatics, Computing, and

Technologies, 3ICT 2022, 344–349.

Nagendra, S., Podila, N., Ugarakhod, R., & George, K.

(2017). Comparison of reinforcement learning

algorithms applied to the cart-pole problem. 2017

International Conference on Advances in Computing,

Communications and Informatics, ICACCI 26–32.

Singh, S. P., & Sutton, R. S. 1996. Reinforcement learning

with replacing eligibility traces. Machine Learning. 22,

123–158.

Surriani, A., Wahyunggoro, O., & Cahyadi, A. I. (2021).

Reinforcement Learning for Cart Pole Inverted

Pendulum System. IEACon IEEE Industrial Electronics

and Applications Conference, 297–301.

Sutton, R. S., & Barto, A. G. (2018). Reinforcement

learning : an introduction. The MIT Press.

Tallec, C., Blier, L., & Ollivier, Y. (2019). Making Deep Q-

learning methods robust to time discretization.

http://arxiv.org/abs/1901.09732.

Tokic, M. (2010). Adaptive ε-greedy exploration in

reinforcement learning based on value differences.

Lecture Notes in Computer Science (Including

Subseries Lecture Notes in Artificial Intelligence and

Lecture Notes in Bioinformatics),6359 LNAI,203–210.

Van Hasselt, H., Guez, A., & Silver, D. (2016, March).

Deep reinforcement learning with Double Q-learning.

The AAAI conference on artificial intelligence (Vol.

30, No. 1).

Wang, Y. H., Li, T. H. S., & Lin, C. J. (2013). Backward

Q-learning: The combination of Sarsa algorithm and

Q-learning. Engineering Applications of Artificial

Intelligence, 26(9), 2184–2193.

Watkins, C. J. C. H., & Dayan, P. (1992). Q-Learning,

Machine Learning, 8(3), 279-292.

Zhong, L. (2024). Comparison of Q-learning and SARSA

Reinforcement Learning Models on Cliff Walking

Problem (pp. 207–213).

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

394