Adaptive Trajectory Prediction in Roundabouts Using Moving Horizon

Estimation

Selsabil Bougherara

, Hasni Arezki

, Chouki Sentouh

1,2

, J

ome Floris

and Jean-Christophe

Popieul

1,2

LAMIH UMR CNRS 8201, Universit

e Polytechnique Hauts-de-France, Valenciennes, France

INSA Hauts-de-France, Valenciennes, France

Keywords:

Moving Horizon Estimation, Trajectory Prediction, Roundabout Navigation, Automated Vehicles.

Abstract:

This paper addresses the challenge of trajectory prediction for automated vehicles navigating within round-

abouts, where interactions, non-linear motion, and rapid decision-making complicate traditional approaches.

We propose a novel prediction framework based on Moving Horizon Estimation (MHE) combined with a non-

linear kinematic bicycle model. Unlike conventional methods such as the Extended Kalman Filter (EKF), the

proposed MHE-based framework leverages past observations over a sliding time window, enhancing robust-

ness against model uncertainties and noise. The method is validated through simulations using the SHERPA

driving simulator in both static and dynamic maneuvering. The results demonstrate that MHE signiﬁcantly

outperforms the EKF in terms of prediction accuracy, particularly during complex vehicle behaviors. This

work constitutes a foundational step toward enhancing safety and robustness of decision-making in round-

abouts.

1 INTRODUCTION

Autonomous driving has made signiﬁcant progress

in recent years, particularly in relatively simple

and well-structured environments such as highways,

where vehicle speed remains nearly constant dur-

ing the decision-making process (Benloucif, 2018;

Oudainia, 2023). For instance, authors of (Guo

et al., 2018) proposed an automated highway merg-

ing strategy that accounts for interactions with sur-

rounding vehicles. However, real-world road envi-

ronments often involve far more complex structures,

such as intersections and roundabouts, where right-

of-way rules, multi-agent interactions, and frequent

trajectory changes make the decision-making process

considerably more challenging. To date, only a lim-

ited number of studies have speciﬁcally addressed au-

tonomous driving in roundabouts. A notable contri-

bution is that of (Bellingard, 2023), who proposed

a decision-making framework for navigation in such

environments. However, this work does not rely on

explicit trajectory prediction, but rather on sensor data

analysis, which can be insufﬁcient when perceived in-

formation is uncertain or incomplete.

Navigating through a roundabout consists of three

main phases: insertion, circulation, and exit. This

study focuses on the insertion phase, which is con-

sidered the most critical, as it requires an immedi-

ate decision: the autonomous vehicle must determine

whether to merge into the circulating ﬂow or yield

to vehicles already in the roundabout. This decision

heavily depends on the ability to reliably predict the

trajectories of nearby vehicles.

In the literature, trajectory prediction methods are

generally categorized into two main groups: para-

metric and non-parametric approaches. Parametric

approaches rely on simpliﬁed physical motion mod-

els, such as constant velocity or constant accelera-

tion models (Schubert et al., 2008), kinematic bicy-

cle models (Kuwata et al., 2008), or dynamic bicycle

models (Brannstrom et al., 2010). While these models

can be effective in simple contexts, they fail to capture

the complexity of maneuvers typically encountered in

roundabouts. They are based on idealized assump-

tions that do not fully account for vehicle kinematics

or the variability of human driving behavior.

Non-parametric approaches, on the other hand,

employ machine learning and deep learning tech-

niques (Huang et al., 2022; Wang et al., 2023).

Several studies utilize Recurrent Neural Networks

(RNNs), particularly Long Short-Term Memory

(LSTM) architectures (Altch

e and de La Fortelle,

380

Bougherara, S., Arezki, H., Sentouh, C., Floris, J. and Popieul, J.-C.

Adaptive Trajectory Prediction in Roundabouts Using Moving Horizon Estimation.

DOI: 10.5220/0013835800003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 380-386

ISBN: 978-989-758-770-2; ISSN: 2184-2809

2017; Park et al., 2018), to model the temporal dy-

namics of vehicle trajectories. Although powerful,

these methods require large amounts of training data

and considerable computational resources, which in-

crease processing time and hinder real-time decision-

making. Other works have proposed more elaborate

behavioral models. For example, Wiest et al. (Wiest

et al., 2012) used Gaussian regression to model the

probabilistic distribution of past trajectories, while

Firl et al. (Firl et al., 2012) employed a hidden

Markov process combined with a reward function to

determine the optimal strategy through dynamic pro-

gramming. However, these methods often assume rel-

atively deterministic motion patterns and struggle to

represent the irregular behavior of human drivers in

complex environments.

In contrast to the above approaches, several prob-

abilistic methods have been developed to explicitly

account for uncertainty in trajectory prediction. The

Extended Kalman Filter (EKF) (Guo et al., 2018) has

been widely used for state estimation but suffers from

linearization errors, especially in nonlinear scenar-

ios such as roundabouts. Monte Carlo-based meth-

ods, such as particle ﬁlters (Gustafsson, 2010), allow

for the representation of non-Gaussian distributions

and can model complex interactions between vehi-

cles (Lef

evre et al., 2014). However, they are compu-

tationally expensive, sensitive to particle degeneracy,

and poorly suited for real-time applications. Another

approach involves the use of stochastic reachable sets,

which aim to encapsulate all possible trajectories un-

der uncertainty while respecting dynamic and envi-

ronmental constraints (Du Toit and Burdick, 2011).

While this method provides formal safety guarantees,

it tends to be overly conservative and difﬁcult to im-

plement online due to its computational complexity.

It is important to note that most of these approaches

have been applied in relatively simple scenarios, such

as highway driving or linear merging situations. In

contrast, our study focuses on a more complex envi-

ronment: predicting the trajectories of vehicles oper-

ating within a roundabout.

To overcome the limitations of existing methods,

Moving Horizon Estimation (MHE) emerges as a ro-

bust and promising alternative for trajectory predic-

tion. Unlike traditional ﬁlters that only consider the

current state, MHE employs a sliding window of past

observations and solves a constrained optimization

problem at each step. This approach enables more

accurate state estimation and facilitates the handling

of physical constraints. Moreover, MHE naturally ac-

commodates nonlinear models without relying on lin-

earization approximations and provides explicit un-

certainty quantiﬁcation. These features make it par-

ticularly well-suited for trajectory prediction in com-

plex urban environments, such as roundabouts.

In this paper, we propose a novel trajectory pre-

diction framework based on Moving Horizon Estima-

tion (MHE), coupled with a nonlinear kinematic bicy-

cle model, for vehicles navigating roundabouts. The

approach can be integrated into a multi-level coop-

erative architecture between human drivers and auto-

mated vehicles to handle complex situations such as

roundabouts. Our method leverages MHE’s robust-

ness in state estimation and employs model propaga-

tion for short-term trajectory forecasting.

Simulation results demonstrate signiﬁcant im-

provements in prediction accuracy and robustness

compared to Extended Kalman Filter (EKF)-based

approaches, conﬁrming the effectiveness of MHE in

handling the complex dynamics and uncertainties in-

herent to roundabout scenarios.

The remainder of this paper is organized as fol-

lows: Section 2 introduces the kinematic bicycle

model used for trajectory prediction. Section 3

presents the proposed MHE-based prediction frame-

work. Section 4 discusses the experimental results

and provides a comparison with the baseline EKF-

based methods. Finally, Section 5 concludes the paper

and outlines directions for future research.

2 VEHICLE MODEL

To represent the motion of surrounding vehicles in

a roundabout, we use a nonlinear kinematic bicycle

model that captures both longitudinal and lateral ve-

hicle dynamics from (Rajamani et al., 2020). Figure 1

illustrates the structure and geometric parameters of

the kinematic bicycle model. The vehicle model is a

single-track model, where the two axles are aligned

and steering is applied only to the front wheel. We

deﬁne the system state vector as:

x =



X Y ψ v



Where X is the longitudinal vehicle position, Y is the

lateral vehicle position, ψ is the vehicle yaw angle,

and v is the speed of the vehicle. Based on the ge-

ometry of the model in Figure 1, the continuous-time

nonlinear state dynamics are written as:

˙x =







vcos(ψ + β)

vsin(ψ + β)

sin(β)







(1)

with

β = tan

−1



+ l

tan(δ

)



Adaptive Trajectory Prediction in Roundabouts Using Moving Horizon Estimation

381

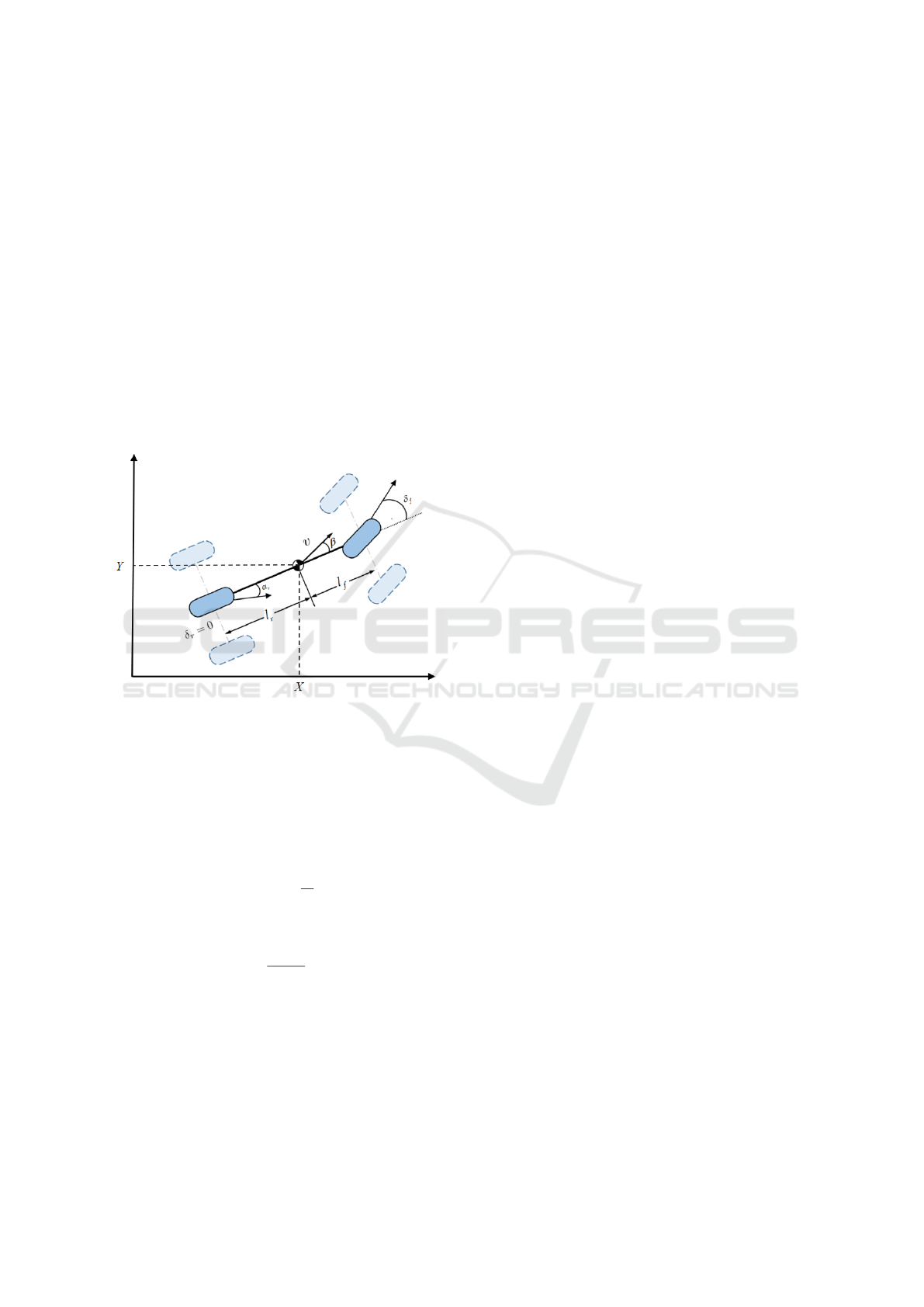
with β is the slip angle at the center of mass, account-

ing for the orientation difference between the velocity

vector and the vehicle’s longitudinal axis. δ

is the

front steering angle. The constants l

and l

represent

the distances from the center of mass to the front and

rear axles, respectively. The output of the system is

given by:

y = Cx, with C =



1 0 0 0

0 1 0 0



Positions X and Y are obtained through vehicle-to-

vehicle (V2V) communication. Finally, we assume

that the rear wheels are not steerable (δ

= 0), as is

the case in most standard passenger vehicles, and that

the acceleration a is either measured or estimated sep-

arately.

Figure 1: Kinematic bicycle model.

The discrete-time nonlinear kinematic bicycle

model is obtained by applying Euler discretization

with a ﬁxed time step ∆t = 0.1 seconds to the

continuous-time dynamics:

k+1

= f (x

)

k+1







+ ∆t · v

cos(ψ

+ β

)

+ ∆t · v

sin(ψ

+ β

)

+ ∆t ·

sin(β

)

+ ∆t · a







(2)

with

= tan

−1



+ l

tan(δ

f ,k

)



3 PROPOSED METHODOLOGY

As emphasized in the introduction, the insertion phase

in roundabouts requires fast and accurate predic-

tion of surrounding vehicle trajectories to enable safe

decision-making. To address the challenge of trajec-

tory prediction in roundabouts, we propose a frame-

work that combines model-based estimation and pre-

diction. A nonlinear kinematic bicycle model is used

to represent vehicle dynamics, offering a good trade-

off between accuracy and computational efﬁciency,

especially for curved trajectories. For state estima-

tion, we adopt Moving Horizon Estimation (MHE),

which outperforms traditional ﬁlters like the EKF by

optimizing over a sliding window and directly han-

dling nonlinearities and constraints, thus improving

robustness to noise, model mismatches, and sudden

changes.

MHE is based on the idea of minimizing a

quadratic estimation cost function deﬁned on a back-

ward sliding window composed of a ﬁnite number

of time stages, which will be denoted by the integer

≥ 1. To this end, we deﬁne the standard quadratic

objective function:

( ˆx

t−N

) = µ

ˆx

t−N

− ¯x

t−N

+ ν

t−1

∑

i=t−N

t−1−i



− h( ˆx

i|t

,0)



(3)

where η ∈ (0,1) and µ,ν > 0 under the con-

straints:

ˆx

i+1|t

= f ( ˆx

i|t

,0), i = t − N

,...,t − 1 (4)

and thus ˆx

t−N

+1|t

,..., ˆx

t|t

are generated by ˆx

t−N

We denote by MHE

what results from the mini-

mization of the cost function (3) as follows:











ˆx

0|t

∈

argmin

ˆx

∈X

( ˆx

)s.t. (4)

holds for t = 1,...,N

ˆx

t−N

∈

argmin

ˆx

t−N

∈X

( ˆx

t−N

)s.t. (4)

holds for t = N

+ 1,N

+ 2,...

together with (4), which provides ˆx

t|t

. For further ease

of presentation, note that the cost function is given by:

( ˆx

) = µ| ˆx

− ¯x

+ ν

t−1

∑

i=0

t−1−i



− h( ˆx

i|t

,0)



(5)

for all t ≤ N

The trajectory of a tracked vehicle is typically pre-

dicted using model-based propagation. This approach

is consistent with the vehicle’s dynamics, as deﬁned

by the discrete-time nonlinear model (2), and enables

accurate state prediction when future control inputs

k+i

(acceleration and steering angle) are known or

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

382

can be reasonably estimated. Moreover, it inherently

respects the physical constraints of the system. An

additional key advantage lies in its computational efﬁ-

ciency: the recursive computation of future states us-

ing the dynamic model can be performed with min-

imal computational cost, making it well-suited for

real-time applications in embedded systems. Given

the discrete-time nonlinear model (2), the predicted

trajectory over a prediction horizon of N

steps is ob-

tained recursively as follows:

ˆx

k+1|k

= f ( ˆx

ˆx

k+2|k

= f ( ˆx

k+1|k

k+1

ˆx

k+N

= f ( ˆx

k+N

−1|k

k+N

−1

(6)

where ˆx

k+i|k

denotes the predicted state at time k + i

based on information available at time k, and N

is the

prediction horizon.

4 EXPERIMENTAL VALIDATION

To validate the applicability of our trajectory pre-

diction approach in a realistic environment, we per-

formed simulations using the SHERPA dynamic driv-

ing simulator of the LAMIH laboratory. SHERPA is a

high-ﬁdelity platform designed to reproduce real-time

vehicle dynamics. The experimental scenario consists

of a single vehicle navigating a multilane roundabout.

The objective is to predict the future trajectory of this

vehicle using only its current and past position mea-

surements, while accounting for the curved motion

typical of roundabout driving. This setup enables a

realistic evaluation of our prediction framework. Fig-

ure 2 shows both the SHERPA simulator and a visual

representation of the roundabout scenario used during

testing.

Figure 2: SHERPA dynamic driving simulator on the

roundabout scenario.

Utilizing the MATLAB Yalmip toolbox, the LMI-

based tuning procedure (Arezki et al., 2023) provides

the following parameters in (3), which are ﬁxed to

µ = 0.01, ν = 1, and η = 0.9. The estimation hori-

zon is set to N

= 10, meaning the MHE optimization

is performed over a backward sliding window of 10

time steps. Additionally, the prediction horizon is set

to N

= 10, enabling the computation of future state

trajectories over 10 steps ahead.

Given the ﬁxed sampling time of ∆t = 0.1 sec-

onds, both horizons correspond to a one-second dura-

tion. This setup allows the MHE framework to simul-

taneously beneﬁt from a sufﬁcient estimation memory

and a meaningful short-term forecast interval. These

parameters were chosen to ensure the robustness and

accuracy of the proposed approach. The initial esti-

mated state is set to



0 0 0 0



⊤

Simulation runs are conducted with both system

and measurement noise, generated according to zero-

mean Gaussian distributions with a covariance of

0.01. For comparison purposes, an Extended Kalman

Filter (EKF) was implemented using the same non-

linear kinematic bicycle model. The EKF was initial-

ized with the same initial estimate as the MHE, and

the process and measurement noise covariances were

selected based on model assumptions and sensor char-

acteristics. The measurement noise covariance matrix

R was constructed using the known standard devia-

tions of the position measurements: 1.5 m for the lon-

gitudinal position and 0.4 m for the lateral position:

R =



(1.5)

0 (0.4)



The process noise covariance matrix Q was set em-

pirically to reﬂect reasonable uncertainty in state evo-

lution, particularly during maneuvers. We assumed

higher uncertainty in velocity and moderate noise in

position and yaw:

Q = diag(0.01, 0.01, 0.001, 0.05)

These values were tuned to ensure stable ﬁlter behav-

ior and allow for a fair comparison with the MHE-

based approach under the same simulation conditions.

4.1 Scenario 1: Without Maneuvering

In this scenario, the vehicle circulates within the

roundabout without executing any maneuvers. It fol-

lows a trajectory with constant acceleration, indicat-

ing the absence of signiﬁcant braking or acceleration

throughout the sequence.

The scenario is illustrated in the following video:

Watch the video on YouTube. Figure 2 shows, on the

left, a thumbnail from the video, and on the right, the

SHERPA simulator equipped with a real vehicle used

for testing.

Trajectory predictions over a one-second horizon,

computed according to the recursive formulation in

Equation (6), are presented in Figures 3 and 6. In

Adaptive Trajectory Prediction in Roundabouts Using Moving Horizon Estimation

383

Figure 3: Comparison of state prediction performance be-

tween MHE and EKF without manoeuvers.

the absence of maneuvers, the MHE consistently pro-

vides predictions that closely match the actual states

obtained from the SHERPA simulator, particularly for

velocity and yaw angle. The EKF exhibits larger devi-

ations, especially during the initial acceleration phase.

These results highlight the superior accuracy and ro-

bustness of MHE, even under steady driving condi-

tions.

4.2 Scenario 2: With Maneuvering

In this scenario, the ego vehicle performs two key ma-

neuvers in response to the presence of a red vehicle

ahead.

Figure 4: Illustration of the vehicle maneuvers in a round-

about scenario. The ego vehicle performs a braking maneu-

ver (in red) to avoid a slower vehicle ahead, followed by an

acceleration maneuver (in green) once the path is clear.

• First, upon detecting the red vehicle, it initiates

a braking maneuver, reducing its speed sharply

Figure 5: Comparison of state prediction performance be-

tween MHE and EKF under manoeuvers

from 30 km/h to 10 km/h in a short time window

in order to maintain a safe distance. This decel-

eration occurs between t = 20 s and t = 22 s, fol-

lowing a constant cruising speed of 30km/h from

t = 0s to t = 20 s.

• Then, once the red vehicle is overtaken or is

no longer obstructing the lane, the ego vehicle

initiates an acceleration maneuver, increasing its

speed from 10km/h to 40 km/h over the interval

t = 22s to t = 30 s.

The speed proﬁle, including the abrupt braking and

smooth re-acceleration phases, was modeled in the

SHERPA simulator using custom event triggers that

modify the vehicle’s control inputs in real time, as

illustrated in Fig. 4. The complete scenario can be

viewed in the following video: Watch the video on

YouTube

Trajectory predictions over a one-second hori-

zon under the maneuvering scenario (Figures 5

and 7), which includes abrupt acceleration and brak-

ing events, show that the MHE maintains accurate

tracking throughout the entire trajectory. The EKF,

however, exhibits notable divergence, particularly in

the lateral and longitudinal positions. These observa-

tions highlight the superior robustness and adaptabil-

ity of MHE, even under dynamic and highly nonlinear

vehicle behaviors.

To compare the performance of the two trajectory

prediction methods, we conducted an analysis based

on the Root Mean Square Error (RMSE) computed

across multiple state variables. The results, summa-

rized in Table 1, demonstrate the superior accuracy of

the MHE approach compared to the EKF, with signif-

icant improvements observed across all metrics.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

384

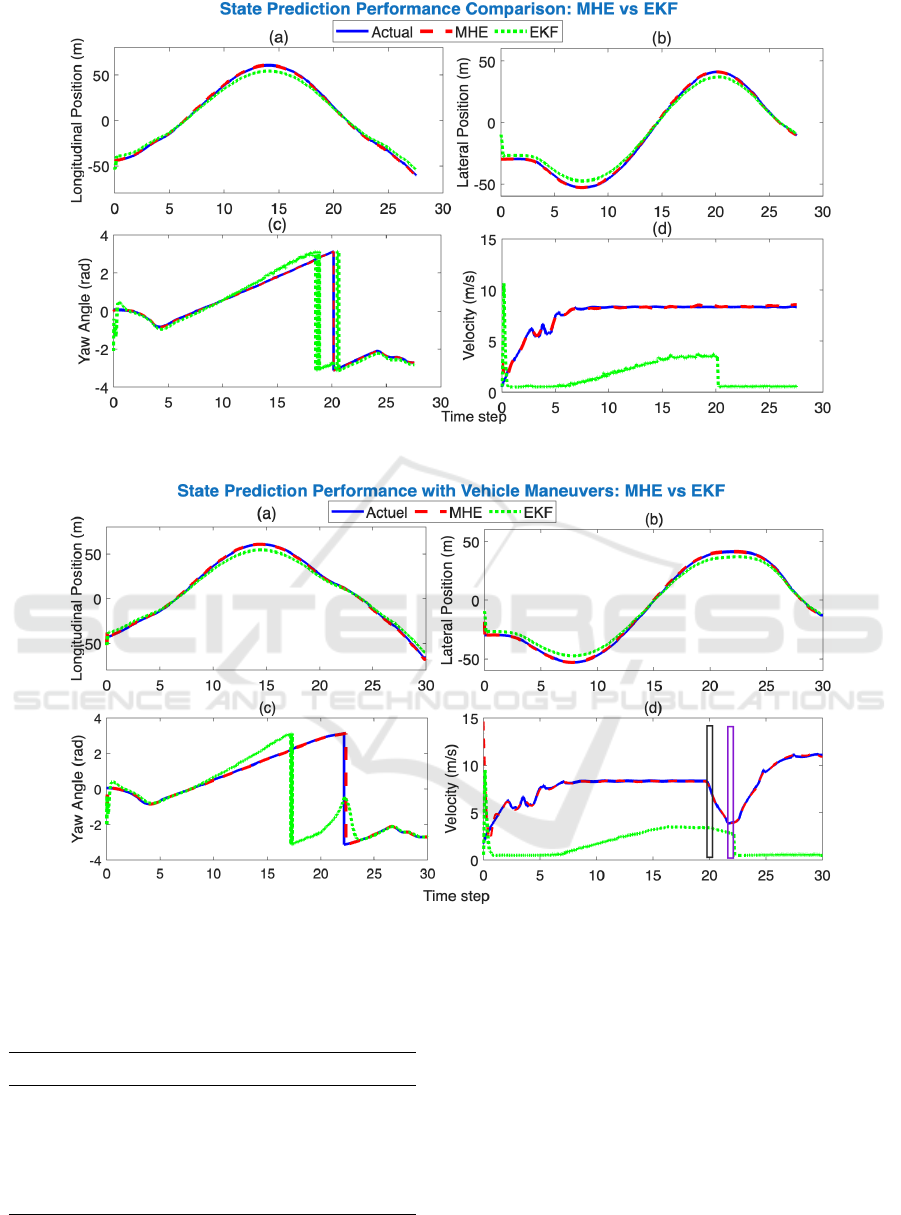
Figure 6: Comparison of state prediction performance between MHE and EKF without manoeuvers.

Figure 7: Comparison of state prediction performance under vehicle maneuvers. The ego vehicle performs two maneuvers:

(1) a braking phase between t = 20 s and t = 22s in response to a slower vehicle ahead (highlighted in black), and (2) an

acceleration phase from t = 22 s to t = 30 s after overtaking (highlighted in violet).

Table 1: RMSE Comparison between MHE and EKF.

Variable MHE EKF Gain (%)

Long. Pos. (m) 0.8790 3.8908 +77.41

Lat. Pos. (m) 0.7133 3.5648 +79.99

Yaw (rad) 0.4845 2.1032 +76.96

Velocity (m/s) 0.5132 6.6501 +92.28

5 CONCLUSION

This work presented a model-based trajectory predic-

tion framework tailored to the complex dynamics of

vehicle motion in roundabouts. By integrating a non-

linear kinematic bicycle model with Moving Horizon

Estimation (MHE), we achieved accurate and robust

state predictions, even under maneuvering conditions.

The comparative analysis with the EKF demonstrated

that MHE provides signiﬁcant improvements in esti-

Adaptive Trajectory Prediction in Roundabouts Using Moving Horizon Estimation

385

mation accuracy and robustness to abrupt behavioral

changes, particularly in lateral and longitudinal posi-

tions, velocity, and yaw angle.

The proposed trajectory prediction framework

lays the groundwork for more advanced decision-

making modules. As a future extension, the pre-

dicted trajectories will be integrated into a risk-aware

decision-making system during the insertion phase

into the roundabout. This integration will subse-

quently be extended to the circulation and exit phases.

Such an approach will enable proactive navigation

strategies and enhance safety in complex, dynamic

environments, where anticipating the behavior of sur-

rounding vehicles is critical.

REFERENCES

Altch

e, F. and de La Fortelle, A. (2017). An lstm network

for highway trajectory prediction. In 2017 IEEE 20th

International Conference on Intelligent Transporta-

tion Systems (ITSC), pages 353–359. IEEE.

Arezki, H., Zemouche, A., Alessandri, A., and Bagner-

ini, P. (2023). Lmi design procedure for incremen-

tal input/output-to-state stability in nonlinear systems.

IEEE Control Systems Letters, 7:3403–3408.

Bellingard, K. (2023). Prise de d

ecision s

ure et robuste

pour les v

ehicules autonomes en milieu urbain haute-

ment dynamique et contraint. Th

ese de doctorat, Uni-

versit

e de Technologie de Compi

egne.

Benloucif, M. A. (2018). Coop

eration homme-machine

multi-niveau entre le conducteur et un syst

eme

d’automatisation de la conduite. Th

ese de doctorat,

Universit

e de Valenciennes et du Hainaut-Cambr

esis.

ffNNT : 2018VALE0012, fftel-01860221f.

Brannstrom, M., Coelingh, E., and Sj

oberg, J. (2010).

Model-based threat assessment for avoiding arbitrary

vehicle collisions. IEEE Transactions on Intelligent

Transportation Systems, 11(3):658–669.

Du Toit, N. E. and Burdick, J. W. (2011). Probabilistic col-

lision checking with chance constraints. IEEE Trans-

actions on Robotics, 27(4):809–815.

Firl, J., St

ubing, H., Huss, S. A., and Dietmayer, K. (2012).

Predictive maneuver evaluation for enhancement of

car-to-x mobility data. In 2012 IEEE Intelligent Ve-

hicles Symposium, pages 558–564. IEEE.

Guo, C., Sentouh, C., Soualmi, B., Hau

e, J.-B., and Popieul,

J.-C. (2018). Adaptive vehicle longitudinal trajectory

prediction for automated highway driving. In IEEE

Intelligent Vehicles Symposium (IV).

Gustafsson, F. (2010). Particle ﬁlter theory and practice

with positioning applications. IEEE Aerospace and

Electronic Systems Magazine, 25(7):53–82.

Huang, Y., Du, J., Yang, Z., Zhou, Z., Zhang, L., and Chen,

H. (2022). A survey on trajectory-prediction methods

for autonomous driving. IEEE Transactions on Intel-

ligent Vehicles, 7(3):258–277.

Kuwata, Y., Teo, J., Karaman, S., Fiore, G., Frazzoli, E.,

and How, J. P. (2008). Motion planning in complex

environments using closed-loop prediction. In AIAA

Guidance, Navigation and Control Conference and

Exhibit.

Lef

evre, S., Vasquez, D., and Laugier, C. (2014). A sur-

vey on motion prediction and risk assessment for in-

telligent vehicles. Robotics and Autonomous Systems,

58(9):1348–1359.

Oudainia, M. R. (2023). Contr

ole partag

e adaptatif et

elaboration de strat

egies de conduite personnalis

ees

pour le v

ehicule automatis

e : une approche par

apprentissage progressif. Th

ese de doctorat, Uni-

versit

e Polytechnique Hauts-de-France. ffNNT :

2023UPHF0038, fftel-04466406f.

Park, S. H., Kim, B., Kang, C. M., Chung, C. C., and

Choi, J. W. (2018). Sequence-to-sequence prediction

of vehicle trajectory via lstm encoder-decoder archi-

tecture. In 2018 IEEE Intelligent Vehicles Symposium

(IV), pages 1672–1678. IEEE.

Rajamani, R., Jeon, W., Movahedi, H., and Zemouche, A.

(2020). Vehicle motion estimation using a switched

gain nonlinear observer. In 2020 American Control

Conference (ACC), pages 3047–3052. IEEE.

Schubert, R., Richter, E., and Wanielik, G. (2008). Com-

parison and evaluation of advanced motion models for

vehicle tracking. In Proceedings of the 11th Interna-

tional Conference on Information Fusion.

Wang, Z., Liu, X., and Wu, Z. (2023). Design of unsignal-

ized roundabouts driving policy of autonomous vehi-

cles using deep reinforcement learning. World Elec-

tric Vehicle Journal, 14(2):52.

Wiest, J., Hoffken, M., Kreßel, U., and Dietmayer, K.

(2012). Probabilistic trajectory prediction with gaus-

sian mixture models. In 2012 IEEE Intelligent Vehi-

cles Symposium, pages 141–146. IEEE.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

386