A Genetic Algorithm for Nash Equilibrium Analysis of Competitive

Course Bidding Mechanisms

Runfeng Yang

Department of Mathematics, Southern University of Science and Technology, Shenzhen, Guangdong, 518055, China

Keywords: Course Bidding, Genetic Algorithm, Discrete Game.

Abstract: This paper analyzes a real course-bidding game that features a discrete and finite strategy set with incomplete

information. Course-bidding systems are widely adopted in academic institutions to allocate limited resources,

yet their strategic dynamics under incomplete information remain understudied. Due to the discrete nature of

the game, a pure strategy derived from Nash Equilibrium is intractable. To address this challenge, this study

employs a Genetic Algorithm (GA) to approximate equilibrium strategies, given the game’s discrete and finite

strategy space. Due to the discrete nature of the game, pure-strategy Nash Equilibria (PSNE) is intractable.

This paper investigates the long-term evolution of strategic tendencies, examining their features and

implications. This study shows that the course-bidding strategy tends to a more concentrated allocation of the

bidding resources. As agents learn to prioritize high-value courses, the resulting strategy leads to higher

variance of the bidding ratios between courses, as well as lowering the width of the courses that are invested.

This analysis reveals structural deficiencies in the model, highlighting the need for mechanisms to mitigate

over-concentration, such as bid caps or quota adjustments.

1 INTRODUCTION

Many schools implement a course selection

mechanism that grants students the liberty to choose

their courses freely (Budish & Cantillon, 2012;

Krishna & Ünver, 2007). For example, at the

Southern University of Science and Technology, each

student is given 100 credits to bid for different

courses, and the courses admit students who bid the

highest credits. This effectively creates an auction

model. Studying this model can help understand the

general impact on students’ course-choosing

strategies, as well as provide insights into the auction

model.

Previous researches on related questions hint at

the unlikelihood of the existence of an equilibrium.

For example, in simultaneous auctions with a

common budget constraint, a symmetric equilibrium

may also fail to exist in terms of first-price auctions

for multiple identical units, which is largely similar to

this study’s case (Ghosh, 2015). However, since the

bids are integral, which disallows fractional

increments, and thus the strategy space is finite, usual

game theory results would generally guarantee the

existence of at least one Nash equilibrium, potentially

a mixed strategy. Let Γ=(N, S, u) be a normal-form

game where strategy sets S are finite due to integer

bidding constraints. By Nash’s existence theorem, at

least one mixed strategy equilibrium must exist.

However, the mixed nature of this strategy makes it

hard to derive a concrete result, especially given the

asymmetric situation that is currently studied.

Krishna and Ünver (2008) conducted a detailed

analysis of a bidding-based course allocation system

used at a business school, focusing primarily on

increasing efficiency through market-clearing

algorithms and preference elicitation. While their

model aligns closely with the one studied here,

particularly in its point-based bidding structure, this

paper diverges by examining the potential

development of the course-bidding strategies in the

long term, which remain underexplored despite their

potentially significant impact on fairness and

outcomes due to the course-bidding strategy shift

over time.

Due to the difficulties mentioned above around

the potential nonexistence of a pure strategy Nash

Equilibrium, a genetic algorithm (GA) is

implemented to evolve student bidding strategies due

to the discrete, non-convex, and highly combinatorial

nature of the course allocation problem. Traditional

optimization fails because (1) payoff discontinuities

584

Yang, R.

A Genetic Algorithm for Nash Equilibrium Analysis of Competitive Course Bidding Mechanisms.

DOI: 10.5220/0013833600004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 584-588

ISBN: 978-989-758-774-0

violate gradient existence conditions, and (2) strategy

space cardinality grows as O(k^n) for k bids and n

students. The underlying mechanism involves

threshold-based admissions and limited bidding

budgets, making the strategy space discontinuous and

poorly suited for traditional optimization techniques.

Additionally, the absence of guaranteed equilibrium

solutions in such auction-based settings further

motivates a simulation-driven approach. The GA

enables us to explore this complex space of behaviors,

uncover emergent patterns, and model how

competitive strategies might evolve over time in

response to systemic constraints.

A Genetic Algorithm (GA) is a heuristic search

technique inspired by the process of natural selection.

Previous works have already explored how to use GA

in a context of game theory. For example, Ismail and

his collaborators studied how a game could be solved

with good performance using GA (Ismail et al., 2007).

Another example could be the Hanabi game, which

also involves incomplete information, studied by

Rodrigo Cannan, who used a GA system to solve the

optimal strategy (Canaan et al., 2018). In general, a

GA algorithm iteratively evolves a population of

candidate solutions toward higher performance by

applying biologically motivated operations such as

selection, crossover, and mutation. Individuals with

higher fitness—defined by a problem-specific

evaluation function—are more likely to pass on their

characteristics to the next generation. Over time, the

population tends to converge toward more effective

solutions, even in complex or poorly structured

search spaces. GAs are particularly useful in domains

where traditional optimization methods fail due to

discontinuities, high dimensionality, or the absence of

gradient information.

GA is long known for its computational merits. It

exhibits key advantages in terms of performance over

the analytical methods (Vié, 2021). First, GA handles

discontinuity extremely well due to the mutation

operators acting as small, random perturbations to

avoid sticking in the local optima. Secondly, since

parallel algorithms are applied, handling situations

where the student and course numbers are huge is

easier. At last, GA mimics the actual student

“experience” passing process in terms of course

choosing, as successful course choosers tend to pass

on their experience to more students in the next year.

In an auction-like context, GA has also presented

a valuable outcome in terms of strategy optimization.

Mochón and the team showed that a GA-assisted

algorithm has the potential to outperform even human

bidders in an auction (Mochón et al., 2005). In the

utility-maximizing context, GA has also been proven

by Choi and his team to have the capability to

optimize or at least improve the overall social utility

(Choi et al., 2018). Even in the notoriously difficult

and complex combinatorial auctions, GA has been

showing potential, as shown by the works of

Karapetyan (Takalloo et al., 2021).

2 CASE DESCRIPTION

This study would examine a hypothetical and

structurally grounded course allocation system

designed to simulate market-based mechanisms for

student enrollment. The model considers a setup

consisting of around 900 students, each with 100 non-

monetary, otherwise not valuable bidding points,

which would serve as their exclusive budget for

getting into courses.

Students are permitted to bid on multiple courses,

distributing their points across them in any proportion

they choose. Each course has a predefined capacity

limit, and the descending order of bids determines

student enrollment at the end of the bidding stage’s

deadline. Once the total number of enrolled students

reaches the capacity of a course, no further students

are admitted.

The allocation system incorporates three non-

standard features. First of all, it is a tiebreaking rule:

in the event of a tie at the cutoff bid, if enrolling all

tied students would exceed the course’s capacity, then

none of the tied students are admitted. This

tiebreaking mechanism introduces strategic

complexity and potential inefficiencies, as it

penalizes coordination and creates uncertainty in

marginal bidding zones. Other than that, another

widely contested feature is the limited information on

the existing bidder’s information, which makes the

expected marginal bidding zone a lot wider than

transparent bidding. A third criticized feature is the

advantage that higher-year students have over lower-

year students due to having fewer common courses

that they need to choose from, which are typically

competitive, giving them more freedom in their

bidding tactics.

This case study aims to evaluate this allocation

model’s behavioral implications, focusing

specifically on the existence of an equilibrium

behavior, strategic bidding dynamics, and the

incidence of tie-related exclusions.

A Genetic Algorithm for Nash Equilibrium Analysis of Competitive Course Bidding Mechanisms

585

3 METHODOLOGY AND

ANALYSIS OF THE PROBLEM

To ensure focus, the model is simplified by

constraining each student to four-course

preferences—two from common and two from

secondary courses—and by evolving only their

bidding strategy rather than their preferences. This

allows us to concentrate on the strategic component

of the allocation problem, avoiding the added

complexity of preference formation or dynamic

utility adjustment, all while still capturing the

competitive behavior under resource constraints.

Also, the size of the student population is reduced,

and the course capacity is leveled to further

concentrate on the strategy itself.

The course allocation system consists of 50 total

courses, subdivided into 10 ‘common’ and 40

‘secondary’ categories. A population of 500 students

each selects two courses from each category to bid on,

resulting in four total course preferences per student.

Each course has a fixed capacity of 20 students. Each

student’s utility vector assigns weight to only four

courses—two from each category. The non-zero

entries are sampled from a uniform distribution and

normalized such that the sum of the utility vector

equals 1. Global popularity for each course is

computed as the proportion of students who have

assigned a non-zero utility to that course. This serves

as a proxy for perceived demand and is used in the

students’ bidding strategy.

For the time being, a naïve softmax-based bidding

model on a linear function would be implemented:

𝑠



𝜃



𝑢



𝜃



𝑝



𝜃



(1)

Each student utilizes a parameterized bidding

function based on personal utility and estimated

course popularity. The score for each preferred course

is computed as above. These scores are passed

through a softmax transformation to get a bid

distribution summing to 100 credits.

Each course allocates seats by descending bid

levels. Starting from a bid of 100, the course admits

all students at each level unless the addition exceeds

its capacity. If admitting a level’s group would cause

overflow, all students at that level and below are

rejected. This is the actual course admission model

used in the university and differs from the usual

lottery tiebreaking system.

Student strategies, defined by the three-

dimensional parameter vector θ, evolve according to

a genetic algorithm. In each generation, strategies are

evaluated based on the benefits gained from admitted

courses. The top-performing individuals, with a 50%

ratio, are selected, and new offspring are generated

via parameter averaging and Gaussian mutation, a

common setup of a GA algorithm.

Fitness is calculated to be the sum of the students’

utility weights for the courses they are successfully

admitted into to measure the students’ strategy’s

efficiency in terms of getting the courses with the

most utility. It is used to evaluate the efficiency of the

overall bidding strategy.

4 RESULT OF ANALYSIS

4.1 Evolution of the Parameters

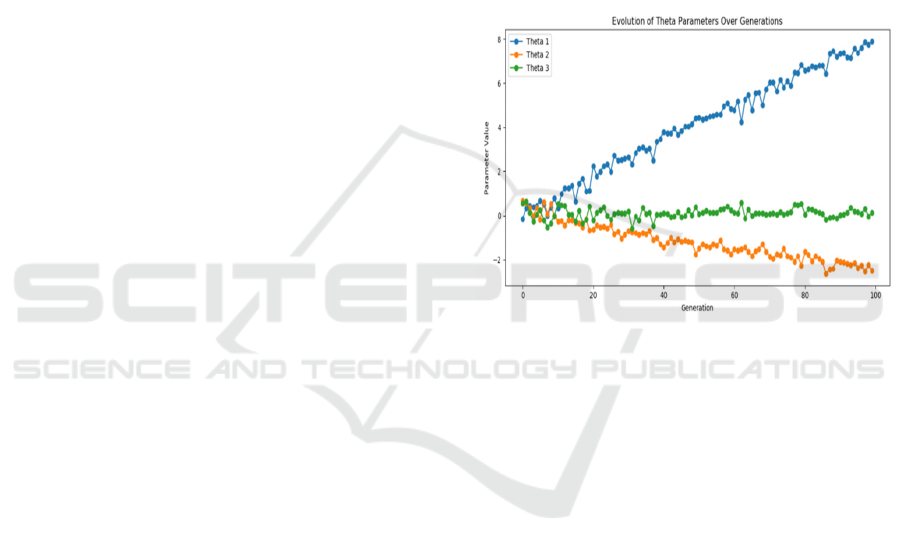
Figure 1: Evolution of the Theta Parameter Over

Generations

Over successive generations, according to Figure

1, the utility weight parameter θ1 exhibited a nearly

linear increase, while the popularity weight θ2 and

bias term θ3 remained relatively constant. This

suggests that the evolutionary process strongly

favored strategies that emphasized personal utility

over collective demand signals. The relative static

behavior of the popularity weight implies that global

popularity provided limited predictive value for

strategic success, possibly due to high competition

and constrained course selection space. These results

indicate that, within the simulated environment,

focusing bids based on individual preferences is a

more effective strategy than attempting to anticipate

or avoid competition.

When seen at a large scale, the weight on

popularity has a slight tendency to drop, yet the

tendency is consistent, which shows that there is a

motive to forsake courses that are over-competed and

focus on other courses.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

586

4.2 Stagnation of the Average Bidder’s

Utility

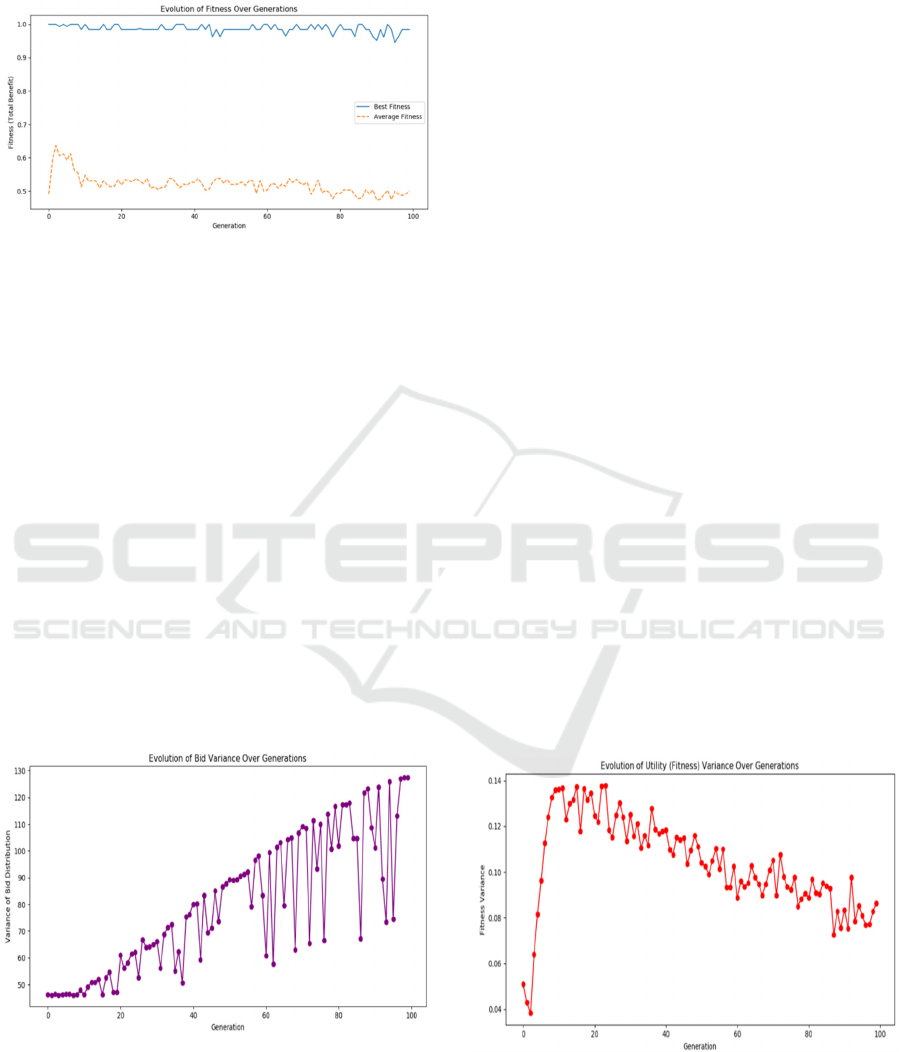
Figure 2: Evolution of Fitness Over Generations

Despite the evolution of high-performing

strategies’ parameters, according to Figure 2, the

average fitness across the population remained

approximately constant at 0.5 throughout the

simulation, after it stabilized after a few generations.

Structural constraints in the system likely account for

this stagnation: with each course admitting only 20

students and each student bidding on just 4 of 50 total

courses, the likelihood of successfully securing any

allocation remains low for the majority of participants.

The allocation mechanism, where those who lost

the course bidding still spend their bidding credits,

and students who are slightly underbid receive no

benefit at all, creates a highly risky environment

where only a few strategies may evolve while the

average strategy is eliminated.

4.3 Enlarged Variations of the Bidding

Credit Distributions

Figure 3: Evolution of Bid Variance Over Generations.

It is observed that, from Figure 3 above, a

consistent increase in the variance of credit

allocations over generations exists, indicating a shift

toward more concentrated bidding strategies.

Vaguely, two linear boundaries are observed, and

they can be interpreted as the influence of the

distribution of the utility over the four chosen courses.

The higher line indicates that the utility is more one-

sided and concentrated on one course, and the lower

line indicates that the utility is more evenly spread

among the four courses. This signifies that the utility

weight is significantly more prominent than other

factors in the GA algorithm. As the simulation

progresses, successful individuals tend to allocate a

larger portion of their credits to one or two preferred

courses rather than distributing them evenly across all

four. This behavior suggests that, given the conditions

in the simulation, the competitive environment favors

aggressive, high-stakes bids (“All-in”) over

diversified, conservative strategies (“Spread-out”).

The rising variance reflects a collective strategic

learning process: students increasingly prioritize

securing admission to a smaller number of high-

utility courses rather than attempting to spread risk

when given a chance to adapt their strategies

repeatedly.

The increase in credit variance reflects an

emergent “all-in” mentality: as competition

intensifies, spreading bids becomes synonymous with

spreading losses. Evolution favors those who

concentrate power, not those who hedge. However,

this would increase the variance of individual

strategies in that if the heavily invested course fails,

the overall expected utility would be extremely low

due to the unlikelihood of being enrolled in the other

courses, due to them being poorly invested.

4.4 The Behavior of the Utility

Variance over the Generations

Figure 4: Evolution of Fitness Variance Over Generations.

The utility variance, according to Figure 4, across

the population followed a two-phase trajectory. In the

initial generations, variance surged as random

A Genetic Algorithm for Nash Equilibrium Analysis of Competitive Course Bidding Mechanisms

587

strategy initialization led to significant disparities in

individual performance. In the early generations, a

subset of students rapidly achieved high fitness due to

the genetic algorithm granting privileges to the fit

strategies, while others consistently failed to secure

course allocations, resulting in a wide spread of

outcomes. As evolution progressed, this variance

gradually declined, reflecting a population-wide

convergence toward more effective bidding

behaviors. The decline suggests that although overall

fitness remained constrained by systemic limitations,

the diversity of outcomes diminished as poor

strategies were eliminated and high-performing

strategies became more common. This suggests that

in the long term, where students actively tutor newer

students on their course-bidding strategy, in the more

rational situation, where students consult older

students who have relatively more successful course-

bidding history, the utility gained by each student

tends to stabilize.

5 CONCLUSION

This paper used Genetic Algorithms to study a

course-choosing system in a real-world situation and

studied its implications. Specifically, this paper aims

to evaluate whether Nash Equilibrium strategies align

with the system’s intended fairness and efficiency

goals. Overall, it is found that this course bidding

system encourages highly concentrated bidding

strategies from the students, yet without significant

contributions to the overall utility gained by the

students on average. Because students converge on

high-demand courses, the resulting scarcity makes the

bidding process inherently more competitive due to

the increased concentration of the credits.

This research again solidified the notion that an

equilibrium strategy may not be the optimal situation

for a system’s intention and that a careful study and

reasoning process should be conducted. However,

since the variance of utility across the students

steadily drops over the generations, this system

exhibits a long-term preference for stable behavior

and fairness in the distribution. It is equally important

to notice that, due to the limited rationality of the

students in real life, this equilibrium is not likely to

be reached, and the overall balance may stick in

earlier generations where the utility variance across

the students is high.

Limitations in this study are noticeable. First of all,

due to the lack of resources, it is not possible to

conduct a census of the students’ actual bidding

strategy, as students tend not even to notice

themselves. Secondly, the usage of a linear soft-max

system in parameter choosing is a compromise

between the complexity of the model and the

generality. Should an alternative model be used, the

results may potentially be different. Finally, it is

worth noticing that actual course bidding strategy

evolution across the generations may be different

from the one that GA represents, which is by mutating

and combining good strategies. In practice, people not

only take advice from other people but also blend in

their internal bias towards the strategy-making

process, complicating the genetics of the strategies.

Future work should incorporate empirical bidding

data and model endogenous strategy mutations

reflecting human biases.

REFERENCES

Budish, E., & Cantillon, E. (2012). The multi-unit

assignment problem: Theory and evidence from course

allocation at Harvard. American Economic Review,

102(5), 2237-2271.

Canaan, R., Shen, H., Rodríguez Torrado, R., Togelius, J.,

Nealen, A., & Menzel, S. (2018). Evolving agents for

the Hanabi 2018 CIG competition. Proceedings of the

2018 IEEE Conference on Computational Intelligence

and Games (CIG), 1–8.

Choi, J.-H., Ahn, H., & Han, I. (2018). Utility-based double

auction mechanism using genetic algorithms. Expert

Systems with Applications, 34(1), 150–158.

Ghosh, G. (2015). Nonexistence of equilibria in

simultaneous auctions with a common budget-

constraint. International Journal of Game Theory,

44(2): 253-274.

Ismail, I. A., El Ramly, N. A., El Kafrawy, M. M., & Nasef,

M. M. (2007). Game theory using genetic algorithms.

Proceedings of the World Congress on Engineering

2007, 2–4 July 2007, London, UK. IAENG.

Krishna, A., & Ünver, M. U. (2007). Improving the

Efficiency of Course Bidding at Business Schools: An

Experimental Study. Marketing Science, forthcoming.

Krishna, A., & Ünver, M. U. (2008). Research note—

improving the efficiency of course bidding at business

schools: Field and laboratory studies. Marketing

Science, 27(2), 262-282.

Mochón, A., Quintana, D., Isasi, P., & Sáez, Y. (2005).

Genetic algorithms versus human bidding strategies for

auctions. In Soft Computing as Transdisciplinary

Science and Technology (pp. 619–628). Springer.

Takalloo, M., Bogyrbayeva, A., Charkhgard, H., & Kwon,

C. (2021). Solving the winner determination problem in

combinatorial auctions for fractional ownership of

autonomous vehicles. International Transactions in

Operational Research, 28(4), 1658-1680.

Vié, A. (2021). A Genetic Algorithm approach to

Asymmetrical Blotto Games with Heterogeneous

Valuations. arXiv preprint arXiv:2103.14372.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

588