Pedestrian Positioning Technology Combining IMU

and Wireless Signals Based on MC-CKF

Seong Yun Cho

and Jae Uk Kwon

Department of Mechanical Engineering, Kyungil University, Gyeongsan, Republic of Korea

Department of IT Engineering, Kyungil University, Gyeongsan, Republic of Korea

Keywords: Maximum Correntropy, Cubature Kalman Filter, IMU, Wireless Positioning.

Abstract: In the paper, the pedestrian position is estimated by integrating the inertial measurement unit (IMU) and the

wireless signal using the Cubature Kalman filter (CKF) based on the maximum correntropy criterion (MCC).

Wireless signals may include short-range wireless communications such as ultra-wideband (UWB) signal and

mobile communication signals such as LTE/5G. UWB can measure distances with an error of less than 30 cm

in a line-of-sight (LoS) environment, but in an environment with LoS, it provides range measurements with

a wide range of non-Gaussian uncertainty errors. In this case, ia an IMU/UWB system is configured with a

conventional minimum mean square error (MMSE)-based filter, significant errors will occur. To address this

issue, this paper designed an MCC-based CKF and applied it to pedestrian positioning technology. Simulation

analysis results demonstrated that the proposed filter is robust to UWB uncertainty and enables reliable

IMUUWB integration.

1 INTRODUCTION

A system integrating an inertial measurement unit

(IMU) and wireless signals is being considered for

indoor pedestrian navigation. An IMU can be

integrated using LTE/5G-based wireless positioning

solutions or ultra-wideband (UWB)-based ranging

measurements. This paper first describes an

integration filter using UWB. UWB enables accurate

range measurements and position estimates in line-of-

sight (LoS) environments, but it is difficult to provide

accurate position information in non-line-of-sight

(NLoS) environments such as indoors because range

measurements include various uncertainty errors

(Banani et al., 2013, Cho, 2019). In order to integrate

IMU and UWB, nonlinear filters such as the extended

Kalman filter (EKF) (Brown and Hwang, 2012) and

the Cubature Kalman filter (CKF) (Arasaratnam and

Haykin, 2009) can be used to take into account the

nonlinear characteristics of inertial navigation and

ranging measurement. However, these minimum

mean square error (MMSE)-based filters do not

adequately respond to UWB uncertainties, potentially

leading to large errors. In this paper, we introduce a

https://orcid.org/0000-0002-4284-2156

https://orcid.org/0000-0001-6222-5043

maximum correntropy criterion (MCC)–based CKF

(MC-CKF) considering this issue.

MCC-based filters are designed based on a kernel

function that maximizes the similarity between the

estimates and the measurement and reflects the error

characteristics of the measurement. The sum of the

kernel function values, including the residuals

calcualted in the measurement update process, is used

as the cost function. And state variables are then

estiamted to maximize this cost function. If

uncertainty errors occur in the UWB measurement,

the MCC-based filter adjusts the P and R matrices to

minimize the impact of measurement uncertainty

errors (Chen et al., 2017, Li et al., 2022).

The purpose of this paper is to apply MCC to CKF

so that it can be used in nonlinear systems. The

designed MC-CKF is applied to a tightly coupled

IMU/UWB system for indoor pedestrian navigation.

The performance of the MC-CKF-based IMU/UWB

integrated navigation system is verified through

simulation. The simulation results confirmed the

following: When UWB measurements contain non-

Gaussian uncertainty errors (Cho, 2019), MC-CKF

significantly adjusts the R matrix corresponding to

Cho, S. Y. and Kwon, J. U.

Pedestrian Positioning Technology Combining IMU and Wireless Signals Based on MC-CKF.

DOI: 10.5220/0013830800003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 375-379

ISBN: 978-989-758-770-2; ISSN: 2184-2809

375

the error measurements to provide stable position

estimates. This is the contribution of this paper to the

field of indoor pedestrian navigation.

2 IMU/UWB INTEGRATION

BASED ON MC-CKF

For integration of an IMU-based inertial navigation

system (INS) with UWB, the state variables are first

set as follows:

x Pos Vel Euler



=∇



(1)

where

and

Vel

are the position and velocity

in the local level coordinate system,

Euler is the

attitude expressed in Euler angles, and

∇ and

are

the accelerometer bias and gyro bias, respectively.

In CKF, these state variables are converted into

cubature points. The number of cubature points is 2N,

and since the system dimension N is 15, there are 30

cubature points.

In CKF, cubature points are time-propagated

using the following INS equations (Farrell and Marth,

1999):

LL L

kkk

Pos Pos Vel dt

−−

=+⋅ (2)

{

}

1,111

,1 ,1 1 1

()

(2 )

LL Lb

kk bkkk

LL LL

ie k eL k k k

Vel Vel C f

Vel g dt

ωω

−−−−

=+ −∇−

+×+⋅

(3)

(

{

)

}

11,11

,1 ,1 ,1

()

kk k ibk k

bL L

Lk iek eLk

QQ Q

Cdt

ωε

ωω

−−−−

−− −

=+ ∗ −

−+⋅

(4)

where

and

are the accelerometer output and

gyro output, respectively,

∇

and

are the estimated

accelerometer bias and gyro bias, respectively, and

is the INS update interval.

is a quaternion,

is the Earth’s angular velocity vector, and

is the

rotational angular velocity vector in the local level

coordinate system caused by the velocity.

When the ranging measurements are obtained via

UWB, the measurement-update is processed in the

CKF. The ranging measurement equation is as

follows (Cho, 2019):

()()

xx yy

jk j k j k jk

rANPosANPosw=−+−+

(5)

where

[]

AN AN

is the position of anchor node

is the j-axis position of the pedestrian in the

local level coordinate system, and

()wj is the noise

contained in channel

j. And {1, 2 , , }jM∈  .

In general,

w in (5) can be modelled as Gaussian

noise in LoS environments. However, in indoor

environments,

w can appear as a non-Gaussian heavy-

tailed impulse error. Considering this, the kernel

function of MC-CKF can be set as follows (Chen et

al., 2017):

( ) exp( / 2 )Ge e

=−

(6)

where

is the kernel bandwidth.

Applying a fixed-point iteration algorithm during

the measurement-update process can improve the

convergence performance of the filter. The P and R

matrices are adjusted as follows:

() ()

()

ki P ki P

PBC B

−−

= (7)

() ()

()

ki R ki R

RBCB

−

= (8)

where

i is the iteration order,

−

and

BR=

−

must be computed before the

measurement-update using the time-propagated

cubature points.

()

and

()

are computed as

follows:

()

(1) 0

0()

Ge N



























 



(9)

()

(1) 0

0()

Ge M



























 



(10)

where

() ( 1)

ˆˆ

()

ki P k ki

eBxx

−− −

−

=− (11)

() ()

()

ki R k ki

eByy

−−

=−



(12)

After the fixed-point iteration algorithm

completes, the state variables and error covariance

matrix are updated as follows:

,() ,() ()

ˆˆ ˆ

()

k k xy k i yy k i k k i

xxP P yy

−− −

=+ −



(13)

() , () , () , ()

k ki xyki yyki xyki

PP P P P

−−

=− (14)

Where

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

376

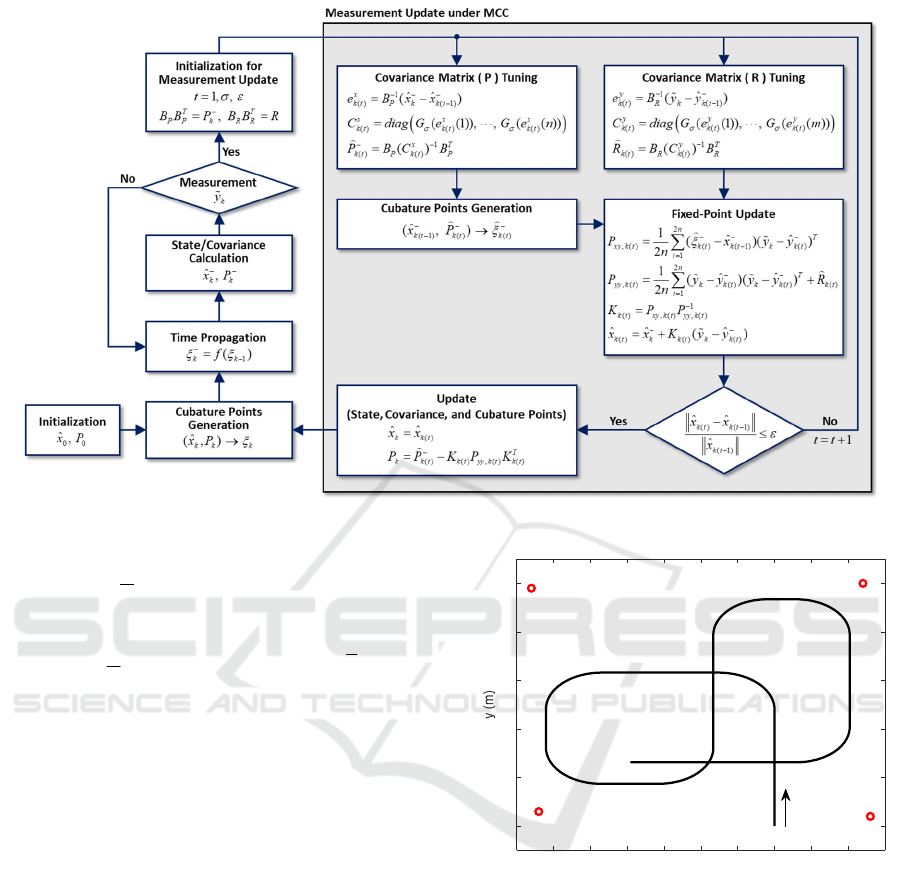
Figure 1: Flowchart of MC-CKF.

,() () ( 1) ()

()()

xyki ki ki k ki

Pxyy

−− −

−

=−−





(15)

,() () () ()

ˆˆ

()()

yyki k ki k ki ki

PyyyyR

−−

=−−+





(16)

where

is the number of the Cubature points.

The proposed filter can be summarized as shown

in Figure 1.

3 SIMULATION ANALYSIS

A simulation was conducted to analyse the

performance of an MC-CKF-based IMU/UWB

integrated pedestrian navigation system in an indoor

space. The pedestrian’s walking trajectory was set as

shown in Figure 2, with four anchor nodes.

The simulation assumes two scenarios: the first is

a LoS environment where only noise exists in the

measurements, and the second is an NLoS

environment where the measurements include biases,

impulse errors, and ramp errors (Cho, 2019).

Figure 2: Simulation trajectory.

Figure 3 shows the results performed in a LoS

environment, and Figure 4 shows the results

performed in an NLoS environment.

In the first simulation, only noise exists in the four

range measurements, so little adjustment of R matrix

is made. Additionally, the positioning results of CKF

and MC-CKF are almost the same, and the heading

estimation performance is slightly improved in MC-

CKF.

0 5 10 15 20 25 30 35 40 45 50

x (m)

AN-1

AN-2

AN-3

AN-4

Pedestrian Positioning Technology Combining IMU and Wireless Signals Based on MC-CKF

377

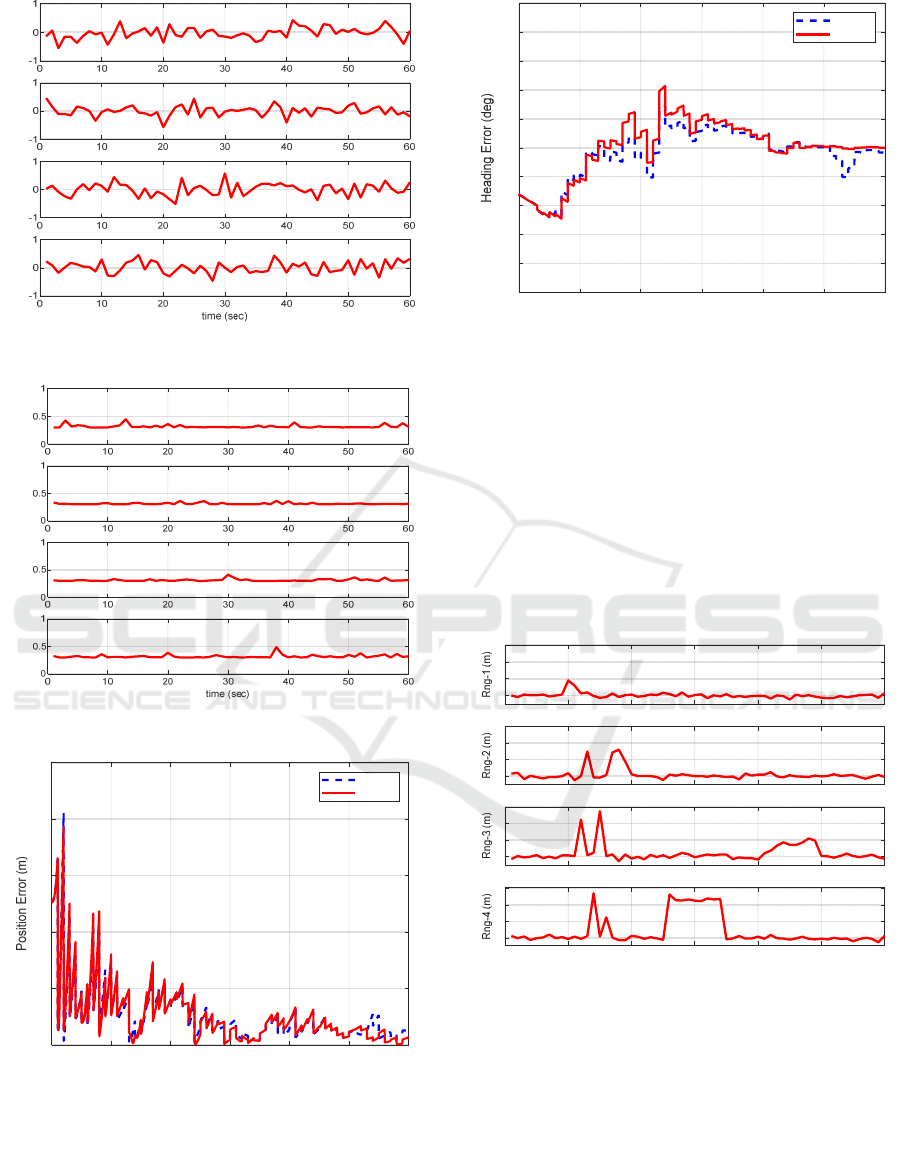
(a) measurement error

(b) square root of adjusted R matrix

(d) heading error

Figure 3: Simulation result in the LoS environment.

In the second simulation, the four range

measurements include not only noise but also impulse,

bias, and ramp errors. Consequently, the adjusted R

matrix of MC-CKF accurately reflects the error

characteristics of each measurement. As a result,

while CKF incurs large position and heading errors

due to the measurement errors, MC-CKF estimates

position and heading information with the same

accuracy as in a LoS environment.

(a) measurement error

Figure 4: Simulation result in the NLoS environment.

Rng-1 (m)Rng-2 (m)Rng-3 (m)Rng-4 (m)

(1, 1) (m)(2, 2) (m)(3, 3) (m)(4, 4) (m)

0 102030405060

time (sec)

0.5

1.5

2.5

CKF

MC-CKF

0 102030405060

time (sec)

-10

-8

-6

-4

-2

CKF

MC-CKF

0 102030405060

time (sec)

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

378

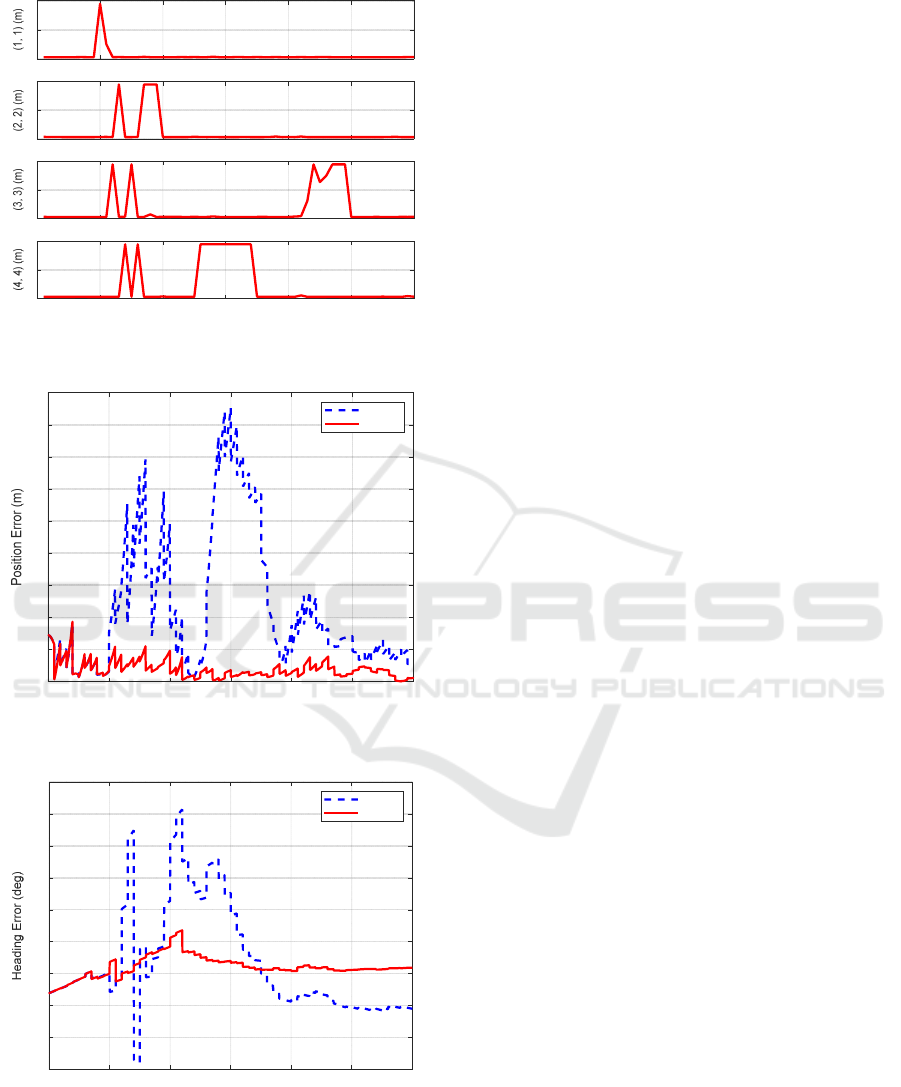
(b) square root of adjusted R matrix

(d) heading error

Figure 4: Simulation result in the NLoS environment

(cont.).

4 CONCLUSIONS

This paper discusses a navigation technology that

integrates an IMU and wireless signals for indoor

pedestrian positioning. UWB uses wireless signals to

measure range information. While range

measurements in LoS environments are only subject

to noise, NLoS environments include bias, impulse,

and ramp errors. In these environments, filters such

as EKF and CKF generate significant positioning

errors. To address this issue, we propose MC-CKF.

This filter recognizes measurement errors and adjusts

the R matrix for each channel. Simulation results

demonstrate that the same positioning accuracy is

maintained in NLoS environments as in LoS

environments.

ACKNOWLEDGEMENTS

This work was supported by Protection Technology

for Socially Vulnerable Individuals Program (www.

kipot.or.kr) funded by Korean National Police

Agency(KNPA, Korea) [Project Name: Development

of an Integrated Control Platform for Location

Tracking of Crime Victim based on Low-Power

Hybrid Positioning and

Proximity Search Technology

/ Project Number: RS-2023-00236101].

REFERENCES

Arasaratnam, I., Haykin, S. (2009). Cubature Kalman

filters, IEEE Trans. Automatic Control, vol. 54, pp.

1254-1269.

Banani, S. S., Najibi, M., Vaughan, R. G. (2013). Range-

based localization and tracking in non-line-of-sight

wireless channels with Gaussian scatterer distribution

model, IET Communications, vol. 7, pp. 2034-2043.

Brown, R. G., Hwang, P. Y. C. (2012). Introduction to

random signals and applied Kalman filtering, John

Wiley & Sons, NJ.

Chen, B., Liu, X., Zhao, H., Principe, J. C. (2017).

Maximum correntropy Kalman filter, Automatica, vol.

76, pp. 70-77.

Cho, S. Y. (2019). Two-step calibration for UWB-based

indoor positioning system and positioning filter

considering channel common bias, Measurement

Science and Technology, vol. 30, pp. 025003.

Farrell, J. A., Barth, M. (1999). The global positioning

system & inertial navigation, McGraw-Hill, New York.

Li, X., Guo, Y., Meng, Q. (2022). Variational vayesian-

based improved maximum mixture correntropy Kalman

filter for non-Gaussian noise, Entropy, vol. 24, pp. 117.

0 102030405060

sqrt(Tuned R matrix)

0 102030405060

time (sec)

0 102030405060

time (sec)

0.5

1.5

2.5

3.5

4.5

CKF

MC-CKF

0 102030405060

time (sec)

-15

-10

-5

CKF

MC-CKF

Pedestrian Positioning Technology Combining IMU and Wireless Signals Based on MC-CKF

379