Linguistic Analogies in Word Embeddings: Where Are They?

Riccardo Contessi, Paolo Fosci

and Giuseppe Psaila

University of Bergamo, DIGIP, Viale Marconi 5, 24044 Dalmine (BG), Italy

Keywords:

Word Embeddings, Linguistic Analogies, Vector Semantics, Semantic Similarity, NLP.

Abstract:

Word Embedding has greatly improved Natural-Language Processing. In word-embedding models, words

are represented as vectors in a multi-dimensional space; these vectors are trained through neural networks, by

means of very large corpora of textual documents. Linguistic analogies are claimed to be encoded within word-

embedding models, in such a way that they can be dealt with through simple vector-offset operations. This

paper aims to give an answer to the following research question: given a word-embedding model, are linguistic

analogies really present? It seems rather unrealistic that complex semantic relationships are encoded within a

word-embedding model, which is trained to encode positional relationships between words. The investigation

methodology is presented, and the results are discussed. This leads to the following question: “Linguistic

analogies in Word Embeddings: where are they?”.

1 INTRODUCTION

Natural-Language Processing (NLP) has achieved

impressive results, which rely on “Neural Networks”:

a large corpus of textual documents is used to train the

inner model of a neural network, following the idea

that if a sequence of words (w

,...,w

) is submit-

ted to the network, it should output the most probable

next w

n+1

word. The internal representation learned

by a neural network trained in this way is a matrix:

rows correspond to single words, while columns de-

note a pool of weights that are used to identify the

most probable w

n+1

word. In such a vision, a word is

represented as a vector in a multi-dimensional space;

the overall pool of vectors (or matrix) is named Word

Embedding.

Modern Word Embedding was introduced by

(Mikolov et al., 2013a), where the above-mentioned

approach was presented. In particular, in the paper,

the authors presented an interesting and remarkable,

although unexpected, feature: the existence of seman-

tic relationships in the form of “linguistic analogies”.

The most famous linguistic analogy can be illustrated

as follows: King stands to Man as Queen stands to

Woman. This analogy gives rise to a very famous vec-

tor operation:

King - Man + Woman ≈ Queen

that could let people think that there is a hidden vector

https://orcid.org/0000-0001-9050-7873

https://orcid.org/0000-0002-9228-560X

(the one that results from King - Man) whose mean-

ing should be “supreme chief”.

As a consequence, many dissemination materials

graphically show such a hypothetic behavior lead-

ing researchers to strongly believe in it. However,

the authors of the present paper wanted to under-

stand Word Embedding, in particular why a word-

embedding model should be able to represent linguis-

tic analogies and semantic relations. Indeed, the exis-

tence of linguistic analogies within word-embedding

models seems quite strange, because an embedding

model is, by nature, a statistical, not semantic, model.

Indeed, many past research works pointed out criti-

cisms about this vision; moreover, it is still a widely

held opinion that linguistic analogies are encoded in

word-embedding models as vector-offset operations.

The goal of this paper is to address the following

research question: given a word-embedding model,

are linguistic analogies really present?

Unfortunately, (Mikolov et al., 2013a) used a dataset

that is no longer publicly available; furthermore, it

empirically showed linguistic analogies by exploit-

ing a vector operation named MostSimilar, which

was not formally deﬁned; although this operation is

present in the Python library Gensim, which is consid-

ered the reference library for managing Word Embed-

dings, it is not clear if it was actually used in (Mikolov

et al., 2013a).

The contribution of the paper is the following:

(i) the concepts of Word Embedding and “linguistic

Contessi, R., Fosci, P. and Psaila, G.

Linguistic Analogies in Word Embeddings: Where Are They?.

DOI: 10.5220/0013830300003985

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Web Information Systems and Technologies (WEBIST 2025), pages 447-458

ISBN: 978-989-758-772-6; ISSN: 2184-3252

447

analogies” are introduced; (ii) the operation Most-

Similar is formally deﬁned, by interpreting the im-

plementation in the Gensim library, and an alternative

(more intuitive) operation named SimilarByVector

(provided by Gensim as well) is considered; (iii) an

investigation methodology is proposed and applied on

a publicly available word-embedding model; (iv) ﬁ-

nally, the results of the experiments are discussed, ob-

taining the question in the title (Linguistic analogies

in Word Embeddings: where are they?).

The novelty of the contribution relies on a substan-

tial criticism to the approaches followed by previous

works: speciﬁcally, visual representations and evalua-

tions have never considered the representational space

actually used by word-embedding models.

The remainder of the paper is organized as fol-

lows. Section 2 brieﬂy resumes the concepts of Word

Embedding and “linguistic analogy”, so as to further

report about related work on the research question of

this paper. Section 3 formally presents the various

vector operations that could be used for managing lin-

guistic analogies. Section 4 introduces the investiga-

tion methodology that was followed to answer the re-

search question, and Section 5 presents the results of

the experiments. Section 6 discusses the results of

the investigation. Finally, Section 7 draws the con-

clusions and highlights possible directions for future

works.

2 BACKGROUND AND RELATED

WORK

The goal of this section is to introduce the background

of the paper and, then, present the related work. Since

all considerations are built around the concepts of

Word Embedding and linguistic analogy, the ﬁrst part

of this section presents these concepts. The second

part discusses the related work.

2.1 Word Embedding

Word Embedding is a technique for Natural-Language

Processing (NLP) that represents a (possibly-large)

vocabulary of words V = {w

,...,w

} in a dis-

tributed way: each term w ∈ V is assigned to a vector

in a d-dimensional space, i.e., given a word w

∈ V

it is represented by a vector v

∈ R

. This con-

tinuous and dense representation should allow for a

more effective capture of relationships among words

in natural language; compared to previously devel-

oped techniques such as bag-of-words (Harris, 1954)

or TF-IDF (Salton et al., 1975), Word Embedding

has largely demonstrated its effectiveness. In recent

years, Word Embedding has led to signiﬁcant ad-

vancements in NLP, due to its ability to geometrically

model similarities and relationships among words.

Formally speaking, given a set of words W =

,...,w

}, an embedding is a function f : W →

that maps each word w

to a vector v

∈ R

(Man-

delbaum and Shalev, 2016).

The vector representation is built in such a way

that vectors that represent words that frequently ap-

pear in similar contexts are located nearby in space.

This reﬂects the idea that the meaning of a word de-

pends on the context in which it is used. Indeed, the

idea is that the semantics of words is implicitly and in-

directly captured: words with similar meaning or that

are strongly correlated are represented by vectors that

point to the same region of space; this is usually true

for words that frequently occur in the same speech

context, such as the relationship between “doctor”

and “hospital”, and, to some extent, syntactic relation-

ships as well, such as the link between verbs and their

inﬂected forms.

Several models propose different strategies to

learn these vectors and they apply different tech-

niques. Word2vec (Mikolov et al., 2013a) leverages

the prediction of local contexts, and relies on a recur-

rent neural network to train the model (indeed, the

embedding is the weight matrix of the inner linear

layer). FastText (Bojanowski et al., 2017) enriches

the representation by exploiting word morphology

through character n-grams, but it still relies on a recur-

rent neural network. GloVe (Pennington et al., 2014)

exploits global co-occurrences within the corpus; dif-

ferently from Word2vec and FastText, the model is

computed as a co-occurrence matrix of words within

the training texts.

Apart from the speciﬁc technical approach, the

idea is as follows: given a sequence of n words

,...,s

), through the word-embedding model it

should be possible to predict the s

n+1

word that is

most likely to follow the given n words.

Although the training process can produce vectors

of different length, models are usually normalized in

such a way that all vectors have length 1; the claimed

reason is to easily compute the cosine similarity be-

tween vectors. As a result, the actual representational

space of a word-embedding model is a d-dimensional

hyper-sphere with radius 1.

2.2 Linguistic Analogies

Linguistic analogies are relationships between pairs

of words, which are based on semantic relationships

between words. A typical example is: a king stands

to a man as a queen stands to a woman. The implicit

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

448

semantic relationship is the concept of “person with

absolute power”. In a more formal way, the above

analogy could be stated as:

(king : man) = (queen : woman)

In the paper (Mikolov et al., 2013a), the authors

launch the idea that the difference between vectors

representing the words in the left and in the right side

of the previous analogy should be two more or less co-

incident vectors, i.e., the semantic relationship “per-

son with absolute power” or “supreme chief” should

be obtained by subtracting the vector “man” from the

vector “king”; similarly, the same vector should be

obtained by subtracting the vector “woman” from the

vector “queen”.

Consequently, given vectors that represent the

words “king”, “man”, and “woman”, the vector

“queen” should be approximately obtained by the

vector operation hereafter reported:

king - man + woman ≈ queen

This property has attracted considerable interest,

as it suggests that the vector space of Word Embed-

dings not only preserves some semantic similarity but

also encodes more complex conceptual relationships.

However, thinking that a representation of words,

which is built to capture co-occurrences of words in

the same speech contexts, is also able to encode se-

mantic relationships within the same representational

space raises several concerns. The purpose of this pa-

per is to investigate this aspect.

2.3 Related Work

The fact that word-embedding models actually en-

code linguistic analogies and semantic relationships

has been long debated. In particular, the fundamental

question is about the way vector operations are per-

formed. The reader can refer to Section 3.1, which

reports a formal deﬁnition of vector operations, as in-

tended by (Mikolov et al., 2013b), in which vectors

representing input words are excluded from the po-

tential result. In this respect, (Linzen, 2016) observed

that if this exclusion is not performed, the correctness

of vector operations drops very close to zero. On the

same line, (Levy and Goldberg, 2014) proposed to

consider the cosine similarity between offset vectors,

but this proposal has not been further followed.

The paper (Rogers et al., 2017) presented a

widespread analysis of critical issues about linguis-

tic analogies in Word Embeddings. However, while

(Rogers et al., 2017) focuses on the statistical per-

spective, the present paper continues on the same way,

by considering the complementary perspective of the

representational space.

In order to test the existence of linguistic analo-

gies in word-embedding models, several authors de-

ﬁned corpora of categorized word pairs. The Google

set was introduced by (Mikolov et al., 2013b) (the

seminal paper about linguistic analogies); the “Bet-

ter Analogy Test Set” (BATS) was introduced by

(Gladkova et al., 2016), with the goal of enriching

the “Google set” with a large number of categories,

choosing a single category for each word (avoid-

ing repetition of words across categories); further-

more, the older corpus of semantic analogies, named

“SemEval-2012” (Jurgens et al., 2012), was used as

a reference of semantic relationships between words

to test analogies (Finley et al., 2017). However, these

data sets are made by humans and can be biased, as

far as the association of a word to a speciﬁc category

is concerned (in case of polysemous words).

Issues related to linguistic analogies emerge for

multi-lingual translations as well, typically managed

through cross-language embedding (Garneau et al.,

2021). Clearly, ways of saying complicate the task,

and simple embedding limited to words could be in-

sufﬁcient.

3 OPERATIONS ON VECTORS

In the literature, a plethora of papers depict the above-

reported example of linguistic analogy with ﬁgures

that are very similar to Figure 1a. However, this repre-

sentation is not accurate and is misleading, for several

reasons.

(i) It does not take into account that the representa-

tional space is a d-dimensional hyper-sphere.

(ii) Points represent words, but words are represented

by vectors in the d-dimensional space, not by points

on a plane or in a 3-dimensional space.

(iii) Furthermore, how vector operations are actually

performed could signiﬁcantly change the result and

affect reproducibility.

Figure 1b provides the correct representation, for

the simpliﬁed case of a 2-dimensional space. First of

all, the vectors that represent words are all rooted in

the origin of axes and reach the sphere (a circle in 2

dimensions) with radius 1; second, notice the effect of

computing a vector offset and later applying it to an-

other vector: the result is outside the representational

space of the 2-dimensional sphere; furthermore, it is

very far away from the expected resulting vector. In-

deed, this is not how vector-offset operations are ac-

tually deﬁned/performed.

In this section, we consider different deﬁnitions,

as they were explored in the literature and beyond,

Linguistic Analogies in Word Embeddings: Where Are They?

449

king

man

woman

queen

(a) Vector operations as usually presented.

king

man

woman

queen

offset

(b) Actual vector operations.

Figure 1: Representations of vector-offset operations.

always considering the actual representation space of

unit hyper-spheres.

3.1 Most Similar

The work (Mikolov et al., 2013a) explored various

vector arithmetic operations to compute linguistic

analogies. To evaluate these relationships, a method

known as MostSimilar, later implemented in the

Gensim library (

Reh

rek and Sojka, 2010), was em-

ployed.

MostSimilar (GenSim Version). Given a set of posi-

tive words P = {w

,...,w

} and a set of negative

words N = {w

m+1

m+2

,...,w

m+n

}, each word w

represented by its embedding vector v

∈ R

• Step 1: Computing the query vector. The

“query vector” v

is computed as a weighted aver-

age of the word vectors from both sets, where each

word is associated with a weight α

∈ {+1,−1}.

Speciﬁcally, α

= +1 if w

∈ P, and α

= −1 if

∈ N. The formula below reﬂects the implemen-

tation of the MostSimilar method in the Gensim

library:

|P| + |N|

∑

∈P∪N

× v

(1)

This formulation ensures that all the vectors,

both positive and negative, contribute to a single

weighted mean rather than computing separate av-

erages.

• Step 2: Normalizing the query vector. The

query vector v

is named this way because it is

later used to query the vector space, so as to ﬁnd

out the closest vector to v

. Since the vector space

is normalized to unit vectors, v

is normalized as

well. Thus, in the following, the normalized ver-

sion v

= norm(v

) is used.

• Step 3: Querying the vector space. Starting

from the normalized query vector v

, the top k

words whose representing vectors v

have the

highest cosine similarity with v

are selected, ex-

cluding the input words in P ∪ N:

MostSimilar(P,N) =

= argmax

w∈V|w /∈P∪N

cos(v

) =

= argmax

w∈V|w /∈P∪N

·v

∥v

∥∥v

∥

(2)

Example. To illustrate, consider a simpliﬁed model

in a 3-dimensional space (d = 3 is clearly insufﬁcient

to obtain an effective model, however it is worth for

the sake of clarity), as illustrated in Figure 2. Specif-

ically, Figure 2a illustrates Step 1, while Figure 2b

illustrates Step 3.

The example of linguistic analogy is:

(trains : train) ≈ (dogs : dog)

consequently, the following vector operation is per-

formed:

trains - train + dog ≈ dogs

where the semantic relationship is “plural of”.

In Figure 2a, the vectors for “train” and “trains”

are the blue and light blue vectors, respectively; for

the sake of clarity, the dashed blue vector depicts “-

train”. Similarly, the vectors for “dog” and “dogs” are

the orange and red vectors, respectively. The resulting

query vector v

is the short fuchsia vector.

Figure 2b focuses on Step 3. For this reason, the nor-

malized query vector v

is depicted (fuchsia vector),

while the vectors for “trains”, “train” and “-train” are

not reported, for the sake of clarity. In addition, the

green vector that represents “puppy” is added. Notice

that in such a conﬁguration, “dog” is still the closest

vector to v

: however, it is not returned because “dog”

is discarded, since it is an input word. Consequently,

usually “dogs” is returned.

MostSimilar (Mikolov Version). In the work

(Mikolov et al., 2013a), a slightly different version

of the vector operation was presented. The difference

concerns Step 1, in which the query vector is com-

puted based on the following equation:

∑

∈P∪N

× v

(3)

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

450

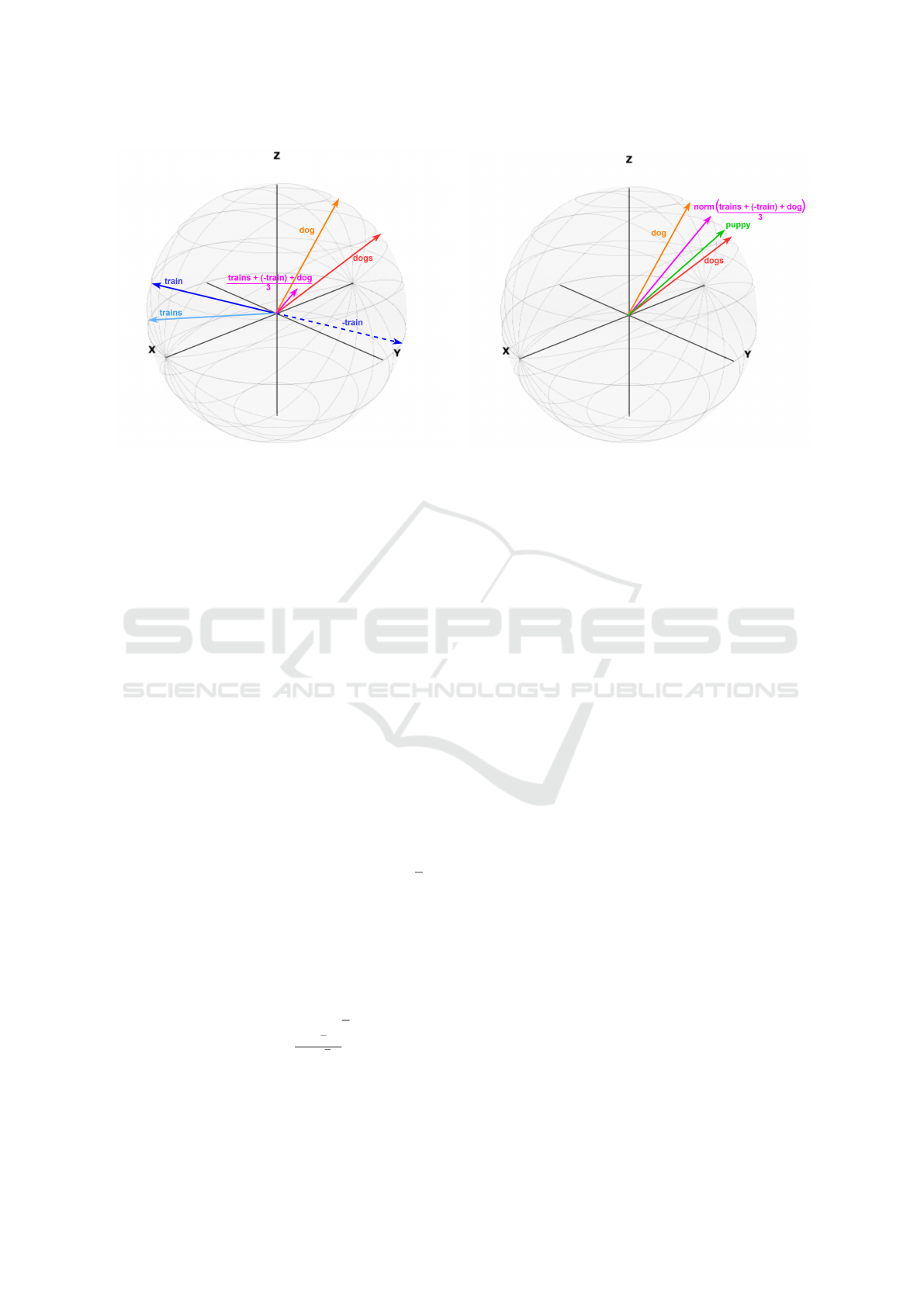
(a) Computing the query vectors. (b) Searching for the most similar vector after normalization.

Figure 2: 3-D visual representation of MostSimilar.

The result is a longer vector compared to the previous

formulation. However, since Step 2 still normalizes

to unit the query vector, Step 3 obtains necessarily

identical results.

3.2 Similar by Vector

A second operation that is provided by Gensim is

named SimilarByVector: the idea is that, once a vec-

tor (that results from a classical vector operation) is

provided, the operation looks for the closest vector in

the model.

• Step 1: Computing the query vector. A simple

sum of vector is performed. However, since the

initial vector is rooted in the origin of the axes, the

resulting vector is also rooted in the origin of the

axes. As an effect, Equation 3 is used to compute

• Step 2: Normalizing the query vector. The

query vector is again normalized to unit, i.e., v

norm(v

) is used.

• Step 3: Querying the vector space. The nor-

malized query vector is used to query the vector

space for the closest vector. This time, all vectors

are considered.

SimilarByVector(P,N) =

= argmax

w∈V

cos(v

) =

= argmax

w∈V

·v

∥v

∥∥v

∥

(4)

Equation 4 is very similar to Equation 2: the only

difference is that all the vectors are considered, while

in Equation 2 input vectors are discarded.

It is worth noting that, due to unit normalization it

could be possible to directly derive SimilarByVector

by simply relaxing the constraint that input vectors

must be excluded from the ﬁnal results.

Example. By exploiting the same example analogy

that was illustrated in the example reported in Sec-

tion 3.1, Figure 3 illustrates the operation Similar-

ByVector.

Figure 3a depicts the computation of the query

vector. Notice that the resulting query vector (fuch-

sia vector) is now longer than the fuchsia vector in

Figure 2a, because each coordinate is now computed

as pure sum of the corresponding input coordinates.

The fuchsia vector in Figure 3b is the correspond-

ing normalized query vector, which is identical to the

normalized query vector depicted in Figure 2b: thus,

the nearby vectors are the same. However, this time

the vector “dog” is obtained because it is the closest

vector and is not discarded (as it is an input vector).

4 METHODOLOGY

This section presents the investigation methodology

that was carried out to address the research question

presented in Section 1.

4.1 Sources

Word Embedding based on the Skip-gram architecture

with Negative Sampling was introduced by (Mikolov

et al., 2013a), which demonstrated the effectiveness

of such models on large text corpora: the model was

Linguistic Analogies in Word Embeddings: Where Are They?

451

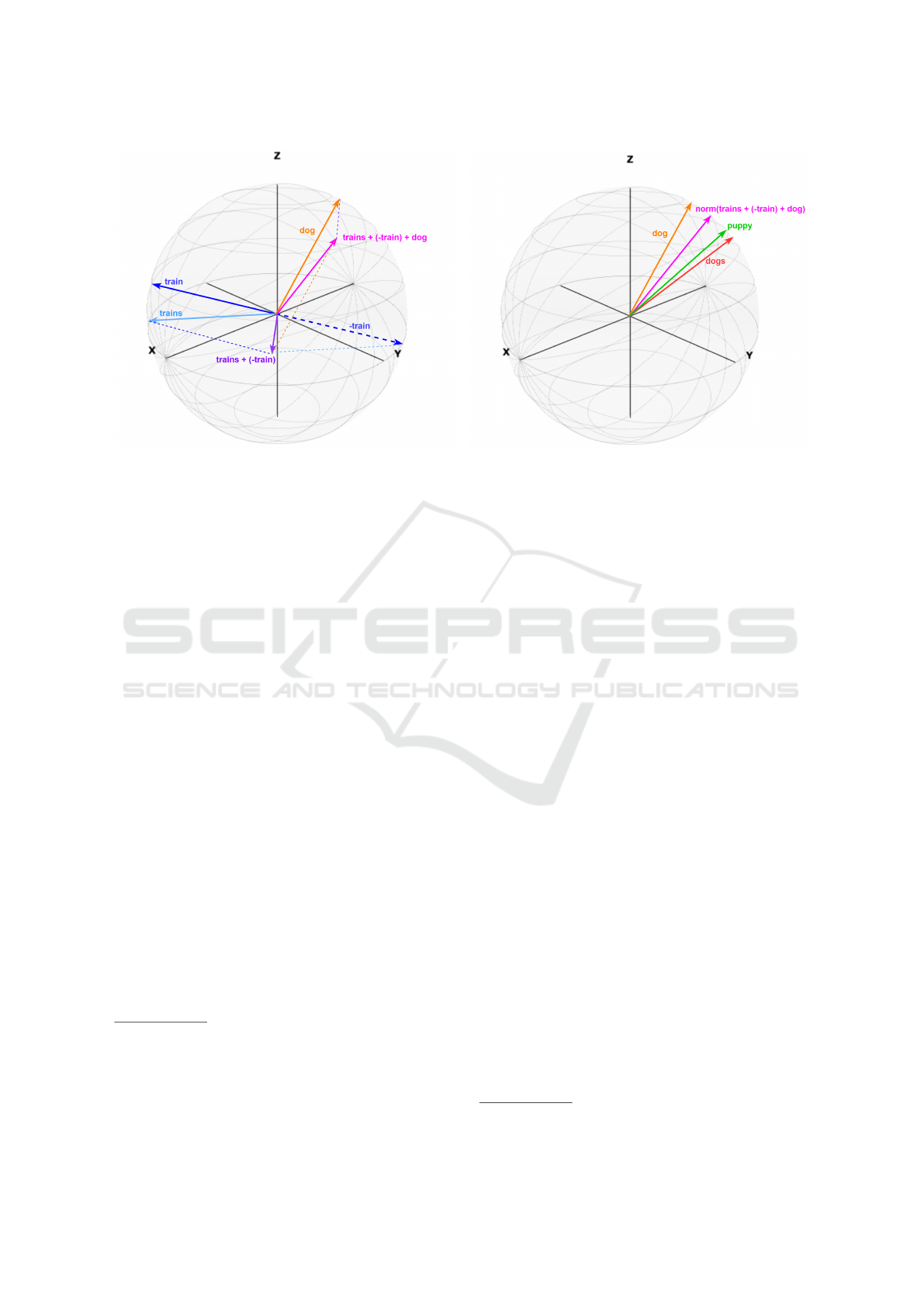
(a) Computing the query vectors. (b) Searching for the most similar vector after normalization.

Figure 3: 3-D visual representation of SimilarByVector.

trained through the Google News dataset

and on the

Wikipedia Text8 corpus

; a 300-dimensional space

was exploited for encoding words within the model.

The word-embedding model so far obtained was

used for the seminal work (Mikolov et al., 2013b), so

as to validate linguistic analogies; however, the word-

embedding model is no longer publicly available at

the link reported in the paper. Consequently, the

present study utilizes a pre-trained model that should

have similar characteristics (as far as training parame-

ters and the Wikipedia training corpus are concerned),

to remain as consistent as possible with (Mikolov

et al., 2013b).

Speciﬁcally, it is the pre-trained Word2vec model,

GoogleNews-vectors-negative300-SLIM.

This model constitutes an optimized and reduced-

vocabulary version of the original GoogleNews-

vectors-negative300 released by Google. The origi-

nal model was trained on approximately 100 billion

words from the English-language Google News cor-

pus, employing the Skip-gram architecture with Neg-

ative Sampling. The SLIM version restricts the vo-

cabulary to the approximately 300,000 most frequent

words and is not normalized to unit length by default

So as to pursue the investigation, the WordNet lex-

ical ontology (Miller, 1995) was downloaded

. In or-

der to query the lexical ontology, the Python library

https://code.google.com/archive/p/word2vec/,

accessed on 15/07/2025.

http://mattmahoney.net/dc/textdata.html,

accessed on 15/07/2025.

https://wordnet.princeton.edu/,

accessed on 15/07/2025.

NLTK was used

Only words conﬁrmed as valid English lemmas

were kept, while very technical or ambiguous terms

were removed.

4.2 Generating Word Pairs

Generation of a signiﬁcant number of word pairs for

a speciﬁc category of linguistic analogy is the neces-

sary starting point. Indeed, the idea is to couple all

the word pairs that share the same type of linguistic

analogy.

Types of Linguistic Analogies. A pool of categories

was considered to automatically build the corpus of

word pairs. This is the only human intervention, i.e.,

choosing the categories of interest; words and word

pairs were automatically built by querying the Word-

Net only, in a totally agnostic way. Hereafter, the con-

sidered categories are presented.

• Capital Cities (e.g., Norway:Oslo). This group

consists of 94 pairs composed of a country name

and its corresponding capital city, illustrating a se-

mantic relationship.

• Currency (e.g., Mexico:peso). Composed of 61

pairs, each formed by a country and its ofﬁcial

currency, representing a semantic relationship.

• Man-Woman (e.g., actor:actress). This set

includes 57 pairs reﬂecting gender-speciﬁc coun-

terparts in professions, roles, or familial relations.

Some pairs are identical due to the existence of

https://www.nltk.org/, accessed on 15/07/2025.

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

452

gender-neutral terms in English (e.g., teacher).

This exempliﬁes a semantic relationship.

• Opposites (e.g., hot:cold). Containing 50 pairs

of antonyms, all adjectives, illustrating syntactic

opposition.

• Comparatives (e.g., tall:taller). This group

consists of 90 pairs of adjectives in their base and

comparative forms, demonstrating syntactic mor-

phological relationships.

• Verb Forms (e.g., work:works). Consisting of

65 pairs illustrating verb forms in the ﬁrst-person

singular and third-person singular present tense,

exemplifying syntactic inﬂection (improperly re-

ferred to as “plural verbs” in (Mikolov et al.,

2013a)).

• Plural Nouns (e.g., chair:chairs). Containing

344 pairs of singular and plural forms of common

nouns. Note that some nouns share identical sin-

gular and plural forms, such as furniture and

species. This represents a syntactic morpholog-

ical relationship.

• Plural Animals (e.g., cat:cats). A subset

of plural nouns focusing exclusively on animal

names, containing 120 pairs. Some animal names

have identical singular and plural forms, such as

sheep and ﬁsh. This is a syntactic morphological

relationship.

• Plurals. The two previous groups “Plural Nouns”

and “Plural Animals” are fused together in a sin-

gle group.

During the experiments, each pair in a group was

compared with all other pairs in the same group. This

explains why three different groups about “plurals”

were considered: “Plural Nouns” were compared to

each other, “Plural Animals” were compared to each

other, and ﬁnally all plurals were compared to each

other (thus, comparing animals with nouns).

Generation Process. Previous corpora of linguistic

analogies (see Section 2) were not considered, in that

since they are mostly created by human beings, they

can be incomplete and can incorporate cognitive bias.

Clearly, semantic relationships that are not encoded

in WordNet were not considered; however, those en-

coded in WordNet are universally recognized and are

not subject to cognitive bias.

The goal was to automate, as much as possible, the

generation of word pairs for speciﬁc categories. Con-

sequently, once categories of interest were deﬁned, a

pool of veriﬁed sets of words from which to start with

the gathering process was established; then, the gen-

eration of word pairs was performed automatically.

The WordNet lexical ontology was the basic

source. However, WordNet does not include factual

relations such as country–currency pairs and coun-

try–capital pairs; for this reason, supplementary re-

sources were needed

. A Python library as pycoun-

try

, actually acquired the factual word pairs.

Morphological and grammatical transformations, in-

cluding pluralization and verb conjugations, were ap-

plied using inﬂection libraries such as inﬂect

, which

handle both regular and irregular forms.

To keep the experimental runtime manageable,

not all possible word pairs were explored. However,

the selected pairs were chosen to be as unbiased and

domain-agnostic as possible.

4.3 Experimental Campaign

The investigation methodology encompassed an ex-

perimental campaign. It was structured as follows.

• For each category C

of word pairs, generated as

described in Section 4.2, each pair p

∈ C

was

coupled with another pair p

∈ C

(both p

and p

belonged to the same category); p

and p

could

coincide.

• Given two pairs p

= (x

) and p

= (x

), the

resulting vector v

was computed.

= v

− v

+ v

Vector operations were performed either by using

the operation MostSimilar or the operation Simi-

larByVector. The word R, represented by v

, was

the retrieved word from the operation.

• If the word R coincided with y

in the pair p

), than the retrieval succeeded, otherwise it

failed.

As anticipated, a ﬁrst round of experiments

was done by performing vector operations through

MostSimilar, while a second round was performed

through SimilarByVector. These two rounds were

necessary to compare the effects of using one opera-

tion in place of the other.

https://en.wikipedia.org/wiki/List of circulating

currencies,

https://en.wikipedia.org/wiki/List of national capitals,

accessed on 15/07/2025.

https://pypi.org/project/pycountry/

https://pypi.org/project/inﬂect/,

accessed on 15/07/2025.

Linguistic Analogies in Word Embeddings: Where Are They?

453

Table 1: Correctness (in percentage) of linguistic analogy

detection using different vector operations (MS stands for

MostSimilar, while SBV stands for SimilarByVector).

Categories

Sample Word Pair

SBV

Capital Cities

Norway

Oslo

78.78%

28.60%

Currency

Mexico

peso

0.75%

0.13%

Man-Woman

actor

actress

39.30%

10.40%

Opposites

hot

cold

12.08%

2.00%

Comparatives

tall

taller

81.35%

11.42%

Verb Forms

work

works

71.44%

13.06%

Plural Nouns

chair

chairs

67.80%

5.21%

Plural Animals

cat

cats

83.14%

9.44%

Plurals

box

boxes

59.38%

4.98%

5 RESULTS

This section presents the results of the experiments

conducted using the methodology described in Sec-

tion 4, comparing the performance of MostSimilar

and SimilarByVector.

5.1 General Overview

Table 1 shows the correctness, expressed as the per-

centage of correctly predicted target words over the

total number of evaluated queries, obtained by using

MostSimilar and SimilarByVector, considering in-

dividually each category deﬁned in Section 4.2. The

table highlights that the two operations behave very

differently, with MostSimilar consistently produc-

ing higher scores than SimilarByVector. This differ-

ence can be attributed to the exclusion of input words

from the pool of potential results that is performed

by MostSimilar. In contrast, SimilarByVector con-

siders all vectors as candidate, without excluding the

input terms, leading to markedly-lower scores.

The performance of MostSimilar aligns with the

benchmarks reported by (Mikolov et al., 2013a). This

way, it is possible to claim that the experimental cam-

paign was performed in a way that is consistent with

the experiments presented in the seminal paper.

5.2 Visual Analysis

A visual analysis was conducted to perform an in-

depth study of results. The heatmaps in Figure 4

presents the results of vector operations considering

word pairs of the category Plural Animals described

in Section 4.2: Figure 4a shows results for MostSim-

ilar; Figure 4b shows results for SimilarByVector.

Each heatmap must be read as follows.

• Vertical axis: Each point in the vertical axis cor-

responds to a word pair in the category; more pre-

cisely, it corresponds to a pair p

= (x

); the

label on the axis is y

− x

• Horizontal axis: A point denotes a pair p

) in the same category, but the label is only

• Point (i, j). A point corresponds to the couple

of word pairs p

= (x

) and p

= (x

). The

point (or cell) denotes the operation

= v

− v

+ v

in such a way that the point is blue if R and y

coincides, otherwise the point is red.

As an example, given cats - cat on the vertical

axis and dog on the horizontal axis, the intersection

point denotes whether

cats - cat + dog

actually returned dogs (blue cell) or a different word

(red cell).

To improve interpretability, the columns are sorted

by retrieval success rate, and the rows are sorted ac-

cordingly. Thus, cells along the diagonal represents

vector operations such as

cats - cat + cat

Figure 4a shows results obtained using MostSimi-

lar. Notice that the heat map is mostly blue, due to the

high rate of correct results; indeed, this is a conﬁrma-

tion of the retrieval rate of 83.14% reported in Table 1

for the analyzed category of “Plural Animals”.

Nonetheless, notice that the cells in the diagonal

are red: indeed, MostSimilar is not able to retrieve

the starting word when a pair is coupled with itself; it

should be

cats

− v

cat

+ v

cat

= v

cats

but MostSimilar does not return cats, because input

words are excluded from the potential results. This is

certainly an anomaly in the design of MostSimilar.

Similar issues arise with words like fish, whose sin-

gular and plural forms are identical. Since these tar-

gets match the input and are ﬁltered out, their retrieval

is impossible with MostSimilar.

Figure 4b shows what happens when Similar-

ByVector is exploited. Recall that the main difference

is that input vectors are not excluded; consequently, it

is possible to expect that the cell on the diagonal are

blue. This can be observed in the heatmap.

However, it performs worse overall, as denoted by

the very large number of red cells. Indeed, this means

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

454

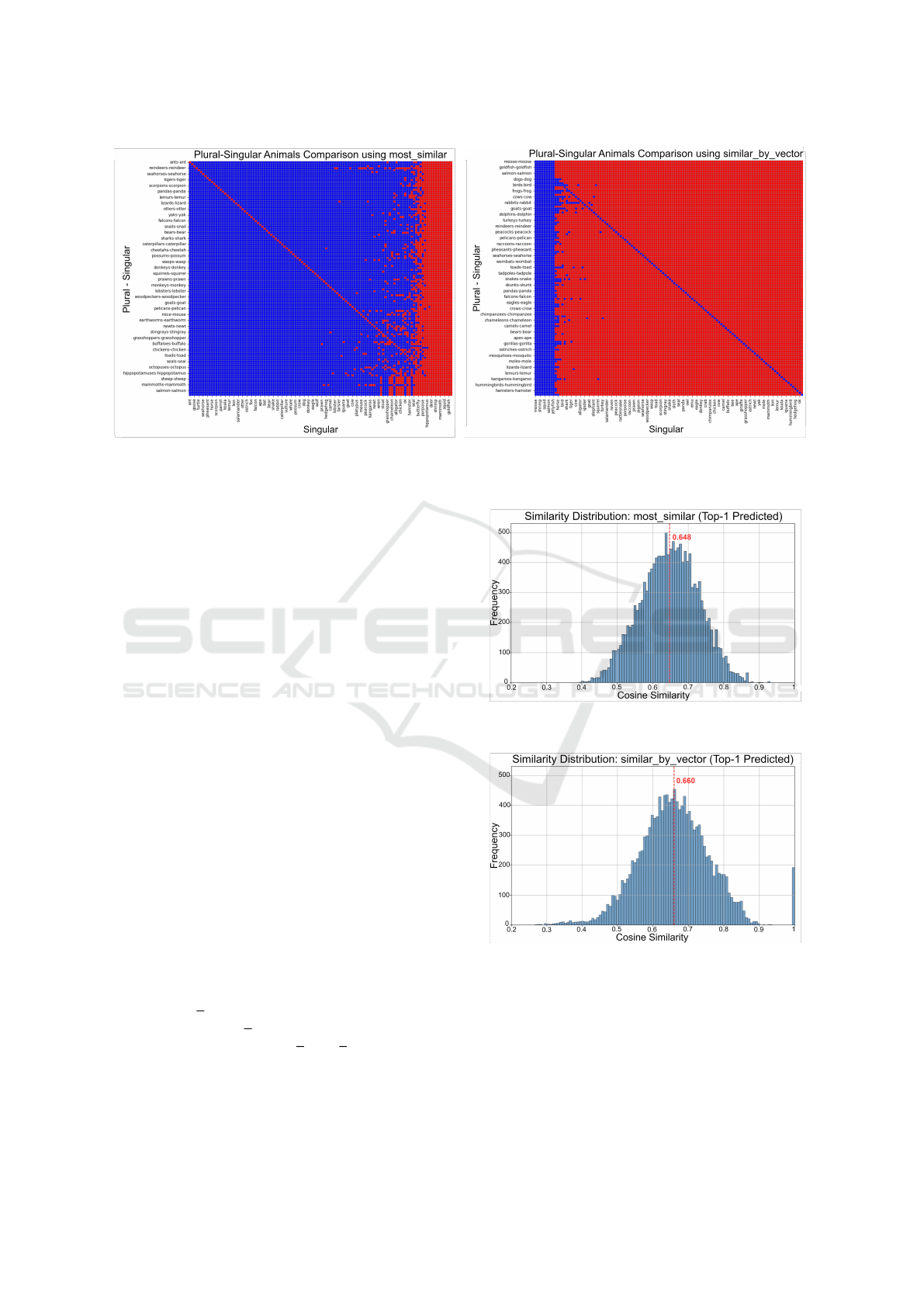
(a) Heat map obtained using the operation MostSimilar. (b) Heat map obtained using the operation SimilarByVector.

Figure 4: Heat maps depicting the correctness obtained for the category “Plural Animals” of linguistic analogies.

that without excluding the input vectors, Similar-

ByVector returns the input vectors as results, mean-

ing that the input vectors are the closest to the query

vector (see Section 3).

Thus, it is possible to interpret the results as fol-

lows: the linguistic category “Plurals Animal” is

rather homogeneous, thus most vectors are in the

same region of space; in particular, vectors represent-

ing singular and plural of the same word are close

enough to each other, allowing MostSimilar to re-

trieve the correct one. However, they are not so close

to the query vector, which in most cases remains close

to the input vector(s), speciﬁcally v

. This is a clear

clue that vector-offset operations do not manage lin-

guistic analogies. The exclusion of input vectors per-

formed by MostSimilar is just an attempt to achieve

the desired result, not considering the intrinsic limi-

tation of the approach, i.e., vector offsets cannot rep-

resent something (linguistic analogies or semantic re-

lationships) that is outside the representational space

(i.e., words).

5.3 Distribution of Cosine Similarity

In order to further conﬁrm the outcomes so far dis-

cussed, a third analysis was made. Speciﬁcally con-

sider both deﬁnitions of MostSimilar and Similar-

ByVector in Section 3. Step 2 obtains the normalized

query vector v

, which is later used in Step 3 to look

for the result vector v

. During all the experiments,

the cosine similarity between v

and v

was measured

and collected.

Figure 5 depicts the collected cosine similarities.

The charts were obtained as hereafter described.

(a) Cosine similarity distribution of the most similar pre-

dicted words using the MostSimilar method.

(b) Cosine similarity distribution of the most similar pre-

dicted words using the SimilarByVector method.

Figure 5: Target correctness matrices comparing singular

and plural animal terms.

• Similarity scores were grouped in intervals of

width 0.1.

• The horizontal axis reports the similarity scores.

Linguistic Analogies in Word Embeddings: Where Are They?

455

• The vertical axis reports the number of pairs

) whose similarity score falls in the inter-

val.

Figure 5a depicts the result for MostSimilar,

while Figure 5b depicts the results for SimilarByVec-

tor.

For the MostSimilar method, it can be observed

that the resulting vectors v

are not overly close to

the query vectors v

, as the average cosine similarity

is 0.646, and in rare cases it is close to 0.9. This corre-

sponds to an angle of about 49.8

◦

between v

and v

meaning that they are somehow far away each other,

they are not particularly close.

Figure 5b depicts the similarity scores for Simi-

larByVector. The reader can see that things do not

change so much: the shape is slightly translated to

the right, results in an average cosine similarity of

0.660. However, this still corresponds to an angle of

approximately 48.5

◦

, meaning that input vectors are

just slightly close to v

so as to be retrieved as results,

but they still remain distant. Furthermore, there are

195 similarity scores that are equal to 1, correspond-

ing to the points seen in the diagonal of Figure 4b plus

additional words whose singular and plural forms are

identical.

Therefore, the very high correctness obtained by

MostSimilar is apparent, in that it excludes the input

vectors that, in most cases, are the closest ones to the

query vector; consequently, it alters the search space

and often retrieves the desired word by chance.

In contrast, SimilarByVector, is mathematically

more adherent to the vector operations; as an effect, it

gets the vector that is actually the closest to the query

vector, which in most cases is not the wished one.

For the sake of space, the analysis is restricted

to the category of “Plural Animals” only. Nonethe-

less, similar results were obtained for the other cat-

egories reported in Table 1. In particular, it is pos-

sible to say that the above considerations are further

stressed when the correctness is lower. This conﬁrms

that the representational space of Word Embedding is

not able to represent linguistic analogies and semantic

relationships in the form of vector-offset operations;

although the research tested only MostSimilar and

SimilarByVector, it can be expected that this is true

for any kind of vector-offset operation.

The fullresults of this experiment are available on

a GitHub repository

GitHub repository:

https://github.com/NLP-Studies-Group/NLP-Studies/

6 DISCUSSION

The results that were obtained by the investigation

methodology ask for a discussion.

Vector operations are not suitable. The results

show that linguistic analogies are not discovered by

the tested vector operations. Both MostSimilar and

SimilarByVector fail to obtain the expected results,

even from a statistical point of view. In fact, assum-

ing that they are somehow encoded within the word-

embedding model, an operation that is actually able

to deal with them should be very effective, with an

correctness that is very close to 1 (considering im-

precision in the training process). MostSimilar and

SimilarByVector certainly are not the wanted opera-

tion.

Lack of Soundness. The idea that linguistic analo-

gies and semantic relationships are encoded in the

word-embedding model is certainly fascinating, how-

ever, all examined previous studies lack formal

soundness. In other words, they move from the hy-

pothesis that linguistic analogies are encoded, thus try

to ﬁnd out a way to let them emerge.

This approach is made evident by the exclusion of

input vectors in MostSimilar: vectors that represent

words that are somehow related to the same speech

context point to the same region of space; conse-

quently, since the difference between two very close

vectors is a small vector (e.g., trains - train), the

addition of a vector that points to a different region

(e.g., dog) obtains a resulting vector that is necessar-

ily very close to the last-added vector (e.g., dog); as

an effect, the last-added vector is very likely to be the

closest one to the normalized query vector.

In other words, it should not be expected that op-

erations that are able to actually deal with semantic

relationships (such as linguistic analogies) can be de-

ﬁned (as vector-offset operations): the reason is that

there is no theoretical foundation that justiﬁes the hy-

pothesis; consequently, it is not reasonable to expect

that they magically emerge.

Indeed, some research work tried to deﬁne a for-

mal framework for word-embedding models and re-

lated vector-offset operations for detecting linguis-

tic analogies, such as (Allen and Hospedales, 2019).

However, the result is a sufﬁcient condition that is

likely not to be met; furthermore, all formulas are still

probabilistic and do not consider the actual deﬁnitions

of vector operations.

Universality of the relationships. Linguistic analo-

gies are “universal semantic relationships”: they ex-

press a concept that applies to all pairs of words for

which it makes sense, independently of the position

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

456

of the vector pairs in the space. Differences of vectors

are not able to capture this universality, because vec-

tor pairs point to different regions of space. Consider,

for example, v

=trains - train and v

=dogs -

dog: v

and v

certainly point to two very different

directions, because the two pairs of input vectors cer-

tainly point to two different regions. However, both

and v

should represent the concept “plural of”, so

they are expected to be very very similar. The conclu-

sion is that it is not possible to expect that the univer-

sal concept of “plural of” could emerge by a vector

operator.

Outside the representational space. Deﬁnitely,

Word Embedding exploits a multi-dimensional space

to represent words in such a way that “positional re-

lationships” are encoded too, so as to be able to gen-

erate the n + 1 most likely word, given a sequence

of n words. Clearly, positional relationships de-

pends on syntactical relationships (that strongly de-

pends on the language); however, these syntactical

relationships are implicitly learned as positional re-

lationships. As an effect, if semantic relationships are

somehow within positional relationships it is because

words whose meanings are strongly related to a given

topic are often in the same speech context, i.e., they

often appear close by. As an effect, it is possible to

assume that words related to similar speech contexts

point to the same region.

Semantic relationships, such as linguistic analogies,

are something different. The analogy “person with

absolute power” does not correspond to any single

word in the vocabulary; thus, there is no vector that

represents it. It is true that words often represent con-

cepts, but it is also true that many concepts are not

represented by simple words.

Consequently, the concept “person with absolute

power” (as a representative of all complex concepts)

cannot be represented within the same representa-

tional space as a single word.

Effectiveness of Word Embedding. Nonetheless,

Word Embedding has been an incredible step towards

effective techniques for NLP. The reason is simple: it

effectively captures “positional relationships”, which

in turn are indirectly related to syntactical and seman-

tic relationships. This is actually the strength of Word

Embedding.

7 CONCLUSIONS

The motivation for this paper was the lasting belief

that word-embedding models actually encode linguis-

tic analogies and structured semantic relationships.

Consequently, the previous works that investi-

gated the existence of linguistic analogies within

word-embedding models were resumed, to reconsider

the problem from a novel perspective: the representa-

tional space and the way vector-offset operations are

deﬁned are the focus of the contribution.

Indeed, after the discussion reported in Section 6,

it appears that vector-offset operations are not the

proper tool to manage structured semantic relation-

ships, because they work in the representational space

of words, i.e., they treat semantic relationships as

they were words; on the contrary, the training phase

considers only positional relationships and implicitly

encodes them within the representational space of a

word-embedding model, by construction.

Deﬁnitely, the results and the considerations that are

presented in this paper conﬁrm what was suggested

by the work (Drozd et al., 2016):, which clearly states

that the essence of Word Embedding is as follows: “all

current distributional semantic approaches rely on the

same basic principle of using similarity between co-

occurrence frequency distributions as a way to infer

the strength of association between words”. Further-

more, the same work claims that “For many practical

purposes, such as information indexing and retrieval

and semantic clustering, these approaches work re-

markably well”. Indeed, since 2013, techniques for

Word Embedding have made possible an incredible

step forward for NLP.

As a future work, the experiments will be ex-

tended to models obtained with different and more

sophisticated techniques, such as BERT. Furthermore,

the authors plan to continue the investigation on the

theme. In particular, a good starting point could be to

move from considerations that were argued by (Etha-

yarajh, 2019), i.e., considering transformations in the

vector space, instead of vector-offset operations.

ACKNOWLEDGEMENTS

This study was funded by the European Union -

NextGenerationEU, in the framework of the GRINS -

Growing Resilient, INclusive and Sustainable project

(GRINS PE00000018 – CUP F83C22001720001).

The views and opinions expressed are solely those of

the authors and do not necessarily reﬂect those of the

European Union, nor can the European Union be held

responsible for them.

Linguistic Analogies in Word Embeddings: Where Are They?

457

REFERENCES

Allen, C. and Hospedales, T. (2019). Analogies explained:

Towards understanding word embeddings. In Interna-

tional Conference on Machine Learning, pages 223–

231. PMLR.

Bojanowski, P., Grave, E., Joulin, A., and Mikolov, T.

(2017). Enriching word vectors with subword infor-

mation. Transactions of the association for computa-

tional linguistics, 5:135–146.

Drozd, A., Gladkova, A., and Matsuoka, S. (2016). Word

embeddings, analogies, and machine learning: Be-

yond king-man+ woman= queen. In Proceedings

of coling 2016, the 26th international conference on

computational linguistics: Technical papers, pages

3519–3530.

Ethayarajh, K. (2019). Rotate king to get queen: Word rela-

tionships as orthogonal transformations in embedding

space. arXiv preprint arXiv:1909.00504.

Finley, G., Farmer, S., and Pakhomov, S. (2017). What

analogies reveal about word vectors and their com-

positionality. In Proceedings of the 6th joint confer-

ence on lexical and computational semantics (* SEM

2017), pages 1–11.

Garneau, N., Hartmann, M., Sandholm, A., Ruder, S.,

Vuli

c, I., and Søgaard, A. (2021). Analogy training

multilingual encoders. In Proceedings of the AAAI

conference on artiﬁcial intelligence, volume 35(14),

pages 12884–12892.

Gladkova, A., Drozd, A., and Matsuoka, S. (2016).

Analogy-based detection of morphological and se-

mantic relations with word embeddings: what works

and what doesn’t. In Proceedings of the NAACL Stu-

dent Research Workshop, pages 8–15.

Harris, Z. S. (1954). Distributional structure. WORD, 10(2-

3):146–162.

Jurgens, D., Mohammad, S., Turney, P., and Holyoak,

K. (2012). Semeval-2012 task 2: Measuring de-

grees of relational similarity. In * SEM 2012: The

First Joint Conference on Lexical and Computational

Semantics–Volume 1: Proceedings of the main confer-

ence and the shared task, and Volume 2: Proceedings

of the Sixth International Workshop on Semantic Eval-

uation (SemEval 2012), pages 356–364.

Levy, O. and Goldberg, Y. (2014). Linguistic regularities in

sparse and explicit word representations. In Proceed-

ings of the eighteenth conference on computational

natural language learning, pages 171–180.

Linzen, T. (2016). Issues in evaluating semantic spaces us-

ing word analogies. arXiv preprint arXiv:1606.07736.

Mandelbaum, A. and Shalev, A. (2016). Word embeddings

and their use in sentence classiﬁcation tasks. arXiv

preprint arXiv:1610.08229.

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).

Efﬁcient estimation of word representations in vector

space. arXiv preprint arXiv:1301.3781.

Mikolov, T., Yih, W.-t., and Zweig, G. (2013b). Linguis-

tic regularities in continuous space word representa-

tions. In Vanderwende, L., Daum

e III, H., and Kirch-

hoff, K., editors, Proceedings of the 2013 Conference

of the North American Chapter of the Association for

Computational Linguistics: Human Language Tech-

nologies, pages 746–751, Atlanta, Georgia. Associa-

tion for Computational Linguistics.

Miller, G. A. (1995). Wordnet: a lexical database for en-

glish. Communications of the ACM, 38(11):39–41.

Pennington, J., Socher, R., and Manning, C. D. (2014).

Glove: Global vectors for word representation. In

Proceedings of the 2014 conference on empirical

methods in natural language processing (EMNLP),

pages 1532–1543.

Reh

rek, R. and Sojka, P. (2010). Software Framework

for Topic Modelling with Large Corpora. In Proceed-

ings of the LREC 2010 Workshop on New Challenges

for NLP Frameworks, pages 45–50, Valletta, Malta.

ELRA. http://is.muni.cz/publication/884893/en.

Rogers, A., Drozd, A., and Li, B. (2017). The (too many)

problems of analogical reasoning with word vectors.

In Proceedings of the 6th joint conference on lexical

and computational semantics (* SEM 2017), pages

135–148.

Salton, G., Wong, A., and Yang, C. S. (1975). A vector

space model for automatic indexing. Communications

of the ACM, 18(11):613–620.

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

458