The Research on the Factors Influencing Housing Prices

Qianyu Shao

Ulink High School of Suzhou Industrial Park, Kunshan, 215300, China

Keywords: Housing Prices, Multiple Linear Regression, Random Forest.

Abstract: This article aims to identify the extent to which certain factors influence housing prices. The author compares

the accuracy and effectiveness of two methods Multiple Linear Regression and Random Forest in analyzing

the significant factors with 1500 samples of the USA in 2014. Based on the multiple linear regression model,

stepwise regression was used to remove the insignificant factor sqft-lot and analyze it to ensure the robustness

of the model. Cross-validation is used to modify the random forest model’s parameters to ultimately produce

the optimal model. The two models present different results. The 7 factors have different impacts on housing

prices in different models. Random Forest is finally shown to be more accurate, the total impact of these seven

factors on housing prices is relatively large. Bathrooms, sqft-lot and city have the biggest effects on home

cost in the more precise random forest method. This study shows that in the future, more timely data can be

selected and control variables can be used to further optimize. This study provides important reference and

guidance for people to predict housing prices.

1 INTRODUCTION

In recent years, real estate price fluctuations have

become one of the core issues in global development.

As time passes, the cost of housing rises annually.

For instance, the average price of a home in China

increased from 1,857 yuan/m2 to 10,375 yuan/m2

between 1999 and 2022, with an average annual

growth rate of 19.94% and a total growth rate of

458.70%. Housing prices have a huge effect on

people’s quality of life, which divides people into

locations with varying advantages. Lower-income

populations are being forced out of core

neighborhoods and into places with less access to

amenities as prices in the city center rise, according

to recent patterns that indicate poverty is becoming

even more sub-urbanized (Hochstenbach and

Musterd, 2018). However, people do not intuitively

understand the factors that affect housing prices, but

housing prices have a great impact on people's lives.

Although a thorough and multifaceted analysis of the

factors influencing home prices has been done in the

literature, more research is still needed. This article

aims to analyze in detail the specific proportion of

different factors affecting housing prices to help

people improve housing quality.

https://orcid.org/0009-0007-5090-7558

Housing prices are influenced by a multitude of

factors, and fluctuations in housing prices are a

significant concern. Zhang also used statistics on

house prices in Wuhan, and their analysis combined

Hypothesis Testing and the Stepwise regression

method. The impact of the Permanent population

urbanization rate, Gross Domestic Product, real estate

development investment, fiscal revenue, and tertiary

industry GDP has been examined. This study took

into account that the population density statistic was

too small and further conducted regression analysis to

improve the accuracy of the linear relationship

(Zhang, 2022). Hamzah et al. found that the primary

factors influencing property prices are supply and

demand by analyzing the total of eight factors that

influence the price of double-story terrace houses in

Bandar Baru Bangi (Hamzah et al., 2012). Zhang

identified the external elements influencing housing

prices with precise data accuracy by utilizing a panel

data model to study the factors affecting housing

prices in seven Chinese megacities (Zhang, 2022).

Aydinoglu and Sisman applied global regression

models including Ordinary Least Squares (OLS),

Spatial Lag Model (SLM), and Spatial Error Model

(SEM) to examine their regional variations

(Aydinoglu and Sisman, 2012). They emphasized that

552

Shao, Q.

The Research on the Factors Inﬂuencing Housing Prices.

DOI: 10.5220/0013829300004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 552-556

ISBN: 978-989-758-774-0

combining local geographic analysis with overall

analysis would make the results more accurate.

Regarding the primary macro factors, Pan indicated

that changes in housing prices in the world's main

nations share certain basic traits, from four aspects of

demand, supply, regulatory policy factors and micro-

consumer factors (Pan, 2021).

However, the current study's analytical

framework exhibits notable limitations in accounting

for geospatial variations, resulting in potentially

biased conclusions. In contrast, Adetunji et al.

systematically demonstrated that while the House

Price Index (HPI) serves as a robust indicator for

regional housing value volatility, it demonstrates

limited applicability in individual property valuation.

Their implementation of Random Forest machine

learning algorithms for price prediction revealed

superior predictive accuracy with reduced error

margins compared to conventional HPI-based

methodologies through rigorous comparative analysis

(Adetunji et al., 2022). Based on geographic data, Liu

et al. used statistics on housing prices in Changsha,

and improved methods of the traditional regression

model to create a geographically weighted model

(GWR) (Liu et al., 2021). The impact of four

parameters(endogenous factors, business location,

transit location and dwelling location). Domestic

scholars have also found that GDP per person and

Demographic shock all affect on housing price (Xu,

2022; Tang, 2016). This paper focuses on these

variables (Bedroom, Bathrooms, Sqft-lot, Floors,

City, Sqft-basement, and Condition) that were

analyzed to establish their impact on housing prices,

and then choose an appropriate model to study the

association between these factors and house prices.

In summary, this article will study the 10 factors

of house prices based on multiple linear regression

model and random forest. This can assist people in

choosing their preferred living area, predicting house

prices, and ensuring their quality of life. This study

will use this model to analyze the impact of these

eight factors and deal with outliers to reduce errors

and ensure the accuracy of the research.

2 METHODS

2.1 Data Source

The datasets were owned by Fırat Özcan and the

usability rate of the datasets is 9.41. The datasets

contain 4138 groups of data and 18 variables from

May to July 2014. The original dataset was in the

.CVS format.

2.2 Variable Selection

The original dataset is a small to medium-sized

dataset and contains many null variables such as

waterfront and view, and the variables of country a

constant (USA). Since the statezip variable has

nothing to do with changes in housing prices, it can

be removed as irrelevant data. At the same time, the

2 variables of year renovated, and street will make the

data form very complicated, so this literature close to

remove these data. Finally, random sampling was

performed to obtain 1500 observations. The data

contains 7 variables (Bedrooms, Bathrooms, Sqft lot,

Floors, City, Sqft-basement and Condition) and one

dependent variable (House price). All 7 variables are

represented in the Table 1:

Table 1: List of Variables.

Variable Meaning

Bedroom The bedroom’s number (0-8)

Bathroom The bathroom’s number (0-6.75)

Sqft-lot The size of lot in square feet (638-1.07m)

Floors The number of floors (1-3.5)

City Location of the house (Seattle: 34%

Renton: 6% Other: 60%)

Sqft-basement The square footage of the basement (0-

4820

)

Condition An indicator that rates the property’s

condition on a scale of 1 to 5 (1-5)

2.3 Method Introduction

In this paper, two classification models are chosen,

which are the multiple linear regression model

(MLR), and random forest model (RF) (Guo et al.,

2022). Comparing the relevance of the two models

and the precision of the findings will be the primary

goals of this section. Finally, it aims to determine the

most suitable model to analyze the relationship

between housing prices and these factors.

The multiple linear regression model is a

parametric model that fits the linear relationship

between multiple independent variables and

continuous dependent variables through the least

squares method. The Random forest integrates

multiple decision trees based on Bootstrap sampling

and feature random selection, outputs prediction

results by voting or averaging, and reduces the risk of

overfitting. The basic formula of the multiple linear

regression model is:

𝑦=𝛽



+𝛽



𝑥



+𝛽



𝑥



+⋯+𝛽



𝑥



+𝜀 (1)

The Research on the Factors Inﬂuencing Housing Prices

553

In the above formula: 𝛽



is a constant term, and 𝜀 is a

residual term.

3 RESULTS AND DISCUSSION

3.1 Multiple Linear Regression

Analysis shows that these 7 variables are all related

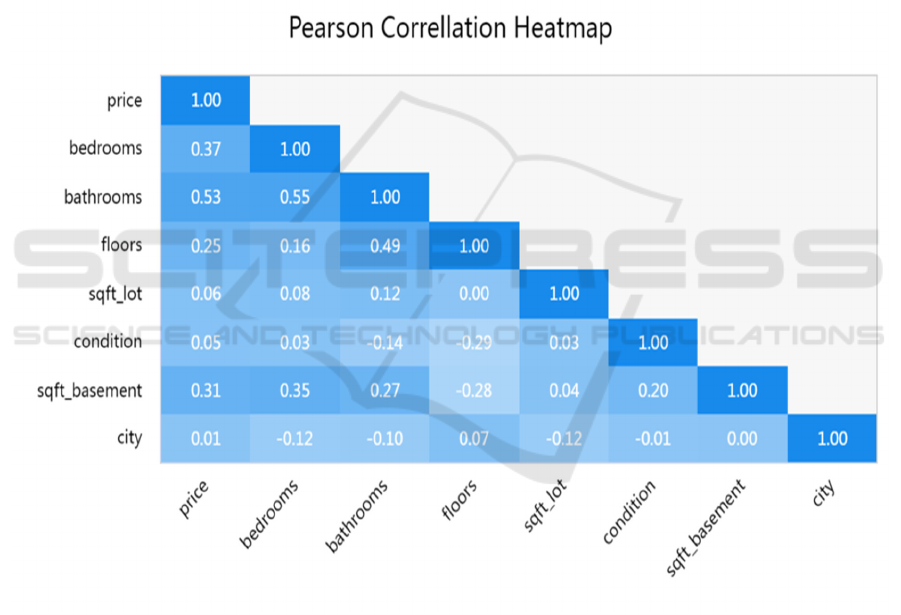
to housing prices. As the graph in Figure 1 shows.

From Figure 1, it shows the relationship between

these factors and housing prices. The data analysis

indicated that the price is significantly influenced by

the following factors: bedrooms, bathrooms, floor,

condition, Sqft-basement, and city. The research data

found that the biggest factor positively influencing

home prices is the quantity of bedrooms and

bathrooms. This indicated that individuals are

becoming more aware of the room types. The data in

the chart clearly shows that the sqft-lot impact on

housing prices is very small compared to other

variables. It is found that people have different

requirements for housing and their needs have

gradually changed from just being able to afford a

house to improving the quality of life.

Figure 1: Relevance Analysis of Dependent and Independent Variables (Picture credit: Original)

Table 2 shows the regression of the multiple linear

regression equation model. The p-values of the T-test

for the variable sqft-lot is greater than 0.05.

Therefore, it indicates that the sqft-lot is not

significant and will not affect housing prices. The

other six variables, on the other hand, all have p-

values below 0.05, suggesting that they significantly

affect house prices.

And about the Variance inflation factor (VIF) values

in this analysis, all of the values are low, ranging from

1.031 to 2.183, well below the accepted threshold of

10. These numbers show that the seven variables are

not collinear, meaning they do not affect one another.

Additionally, the Tolerance values range from 0.458

to 0.97, demonstrating that every predictor variable in

the model offers distinct information that is not

duplicated by other variables. As a result, regression

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

554

models including these variables are expected to have

stable and trustworthy coefficients, enhancing the

accuracy of this research.

Table 2: Linear regression analysis results.

B S.E. Beta t p VIF Tolerance

Constants -304963.467 56873.717 - -5.362 0.000** - -

bedrooms 24607.386 10028.333 0.065 2.454 0.014* 1.562 0.64

bathrooms 176101.81 13668.024 0.401 12.884 0.000** 2.183 0.458

sqft_lot 0.045 0.175 0.005 0.254 0.799 1.031 0.97

floors 84174.332 18126.773 0.132 4.644 0.000** 1.816 0.551

condition 50227.899 11151.592 0.1 4.504 0.000** 1.121 0.892

sqft_basement 146.287 19.044 0.199 7.681 0.000** 1.517 0.659

city 1786.762 689.751 0.056 2.59 0.010** 1.061 0.943

Note: * p<0.05 ** p<0.01

3.2 Multiple Linear Regression with

Backward Elimination

From the above analysis, it can see that sqft-lot has

almost no impact on housing prices. For this variable,

this study uses the backward elimination method in

stepwise regression to remove this variable to make

data analysis more effective. It can be seen that all P

values are within the accepted range. This indicates

that all six variables are explicit.

Table 3: Results of Backward Elimination Regression

Note: * p<0.05 ** p<0.01

According to table 3, all variables have high

significance, although they haven't altered much from

their prior values. These data show the 6 variables

have a significant positive effect on house price.

Therefore, it will derive a model: price =

304678.104 + 24628.129 ∗ bedrooms + ⋯ +

1769.550 ∗ city.

3.3 Random Forest Results

This paper will also use the random forest model to

analyze the impact of these 7 factors on housing

prices, and then compare it with the multiple linear

regression model to find the most suitable model for

the impact of housing prices. The total amount of data

analyzed this time is 1500, and random forest selects

80% of them for analysis. The optimal parameters

obtained were 100 for “ntree” and 2 for “mtry” The

final fitting using the best parameters yields an

optimal random forest model. Eventually, Figure 2

displays the result of the random forest.

Figure 2: Feature Weight of RM Model (Picture credit:

Original)

Variables B S.E. T P

Constant -304678.104 56844.847 -5.360 0.000**

bedrooms 24628.129 10024.860 2.457 0.014*

bathrooms 176448.015 13595.883 12.978 0.000**

floors 83960.099 18101.539 4.638 0.000**

condition 50336.577 11139.920 4.519 0.000**

basement 146.163 19.032 7.680 0.000**

city 1769.550 686.211 2.579 0.010*

The Research on the Factors Inﬂuencing Housing Prices

555

From Figure 2 it can be seen bathrooms, sqft-lot, and

city these 3 influencing factors account for 72.87% of

the total. Therefore, the other four factors have little

impact on housing prices. This reflects that these 3

factors have a great impact on housing prices, while

the other four variables (bedrooms, floors, condition,

sqft-basement) have almost no impact on house

prices.

Table 4 shows the accuracy of the model is

obtained as after prediction on the test set, and the R-

squared for fitting the random forest model is 0.497

when testing, 0.921 when training.

Table 4: Results of Random Forest.

4 CONCLUSION

Overall, this study selected 1500 samples from all of

4120 from the data set, which has 7 variables. By

comparing the performance of the two models,

Multiple Linear Regression and Random Forest, on

the impact of house prices. Based on the multiple

linear regression, it was concluded that sqft-lot was

an insignificant factor. Therefore, a stepwise

regression model was further used to remove

inaccurate variables, and finally, effective and

accurate results were obtained. Another model

random forest analysis and obtained the Feature

Weight Graph to intuitively understand the

proportion of each variable affecting housing prices.

Comparing the R-squared values of the two methods,

the random forest has a larger value. Therefore, the

total impact of the seven factors calculated by the

random forest on housing prices is greater. As a

result, a variety of factors influence how well various

models function. In various investigations, the author

should choose the most correct model to examine

after identifying the key characteristics of the data.

With this research, people can have more

references when choosing their ideal house and have

an approximate idea of how much houses will cost.

However, most of the data in this study are from 2014,

which has certain time limitations and a small sample

size. Using control variables and locating more recent

data might enhance this analysis.

REFERENCES

Adetunji, A. B., Akande, O. N., Ajala, F. A., 2022. House

price prediction using random forest machine learning

technique. Procedia Computer Science, 199, 806-813.

Aydinoglu, A. C., Sisman, S., 2012. A modelling approach

with geographically weighted regression methods for

determining geographic variation and influencing

factors in housing price: A case in Istanbul. Land use

policy, 119, 106183.

Guo, H. P., Qian, Y. H., Zhu, Y., 2022. Statistical inference

method of factors affecting housing prices. Statistics

and Management, 37(05), 58-63.

Hamzah, N., Khoiry, M. A., Tawil, N. M., 2012. Critical

factors affecting double storey terrace houses prices in

Bandar Baru Bangi. Procedia-Social and Behavioral

Sciences, 60, 562-566.

Hochstenbach, C., Musterd, S., 2018. Gentrification and the

suburbanization of poverty: changing urban

geographies through boom and bust periods. Urban

Geog, 39, 26-53.

Liu, Y. P., Tang H. T., Wu, Z. C., 2021. Spatial

heterogeneity analysis of factors affecting housing

prices based on POI data: A case study of Changsha.

Urban Issues, 2, 95-103.

Pan, T., 2021. A review of research on factors affecting

housing prices. Guangxi Quality Supervision Herald, 2,

5-7.

Tang, W. B., 2016. An empirical analysis of the factors

affecting real estate prices in my country. Price Theory

and Practice, 1, 119-121.

Xu, H., 2022. Analysis of factors affecting housing prices

in Jiangsu Province. Market Weekly, 35(04), 46-50.

Zhang, Y., 2022. Analysis of factors affecting housing

prices in my country's megacities. University of

International Business and Economics.

Training Accuracy Test Accurac

R2 0.921 0.497

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

556