Diabetes Risk Assessment: A Logistic Regression Modelling Study

Based on Large-Scale Data

Haotian Sun

, Haoning Tian

and Fan Zhang

3,* c

Wuhan Britain-China School, Wuhan, Hubei, 430030, China

School of Mathematics, Tianjin University of Finance and Economics, Tianjin, 300222, China

Faculty of Science, University of Alberta, Edmonton, Alberta, T6G2G5, Canada

Keywords: Diabetes, Risk Assessment, Logistic Regression, Random Forest.

Abstract: As a major global public health problem, early diagnosis and accurate risk assessment of diabetes are of great

significance for disease prevention and control. Based on machine learning methods, this study systematically

explored the application efficiency and clinical value of logistic regression (LR) and random forest (RF)

algorithms in diabetes prediction. The study used a clinical data set of 768 observations to construct a

prediction model by analyzing key health indicators such as blood glucose level, BMI index, age, number of

pregnancies, and diabetes pedigree function. The results showed that the LR model showed good prediction

performance with an accuracy of 78.26%, among which blood glucose level, BMI index, number of

pregnancies, and diabetes pedigree function were identified as the most statistically significant predictors.

The RF model (500 decision trees) showed a stronger ability to capture nonlinear relationships, with an

accuracy of 74.03% and an AUC value of 0.831. Feature importance analysis showed that blood glucose,

BMI, and age contributed the most to prediction. LR provides clear clinical interpretability, which helps

doctors understand the impact of each risk factor; RF can effectively identify complex interactions between

variables.

1 INTRODUCTION

Diabetes mellitus has long been a major global health

challenge due to its chronic and progressive nature. It

is mainly characterized by chronically elevated blood

glucose levels, caused by insufficient insulin

secretion or insulin dysfunction, and common types

include type 1 diabetes, type 2 diabetes, and

gestational diabetes. According to the World Health

Organization, in 2012, diabetes directly caused 1.5

million deaths and an additional 2.2 million deaths

due to cardiovascular disease caused by

hyperglycemia, and the global prevalence of diabetes

has increased from 180 million cases in 1980 to 422

million cases in 2014 (Roglic, 2016). It is meaningful

to analyze the factors of diabetes, such as gender,

since the challenge caused by diabetes is more serious.

As the Gale study shows that men are more likely

to develop type 2 diabetes at a younger age, while

https://orcid.org/0009-0000-7575-4737

https://orcid.org/0009-0004-8221-8560

https://orcid.org/0009-0007-4588-5999

women's risk rises significantly after menopause, the

impact of gender on diabetes has been widely

publicized. In addition, female patients have a higher

risk of cardiovascular disease than men (Gale &

Gillespie, 2001).

Other researchers’ studies show that biochemical

indicators are strongly associated with diabetic

complications. Lewis et al. (2005) found that high

homocysteine levels were associated with a

prevalence of diabetic nephropathy as high as 93.3%,

with a 7.15-fold increase in risk. Dehghan's study

demonstrated that C-reactive protein (CRP) levels

were independently associated with the risk of

diabetes, and that genetic variants may increase

susceptibility (Dehghan et al., 2007).

Lifestyle factors are also important influences.

Carlsson’s meta-analysis found that moderate alcohol

consumption reduced the risk of type 2 diabetes by

30%, but this effect has been less well studied in

464

Sun, H., Tian, H. and Zhang, F.

Diabetes Risk Assessment: A Logistic Regression Modelling Study Based on Large-Scale Data.

DOI: 10.5220/0013827600004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 464-469

ISBN: 978-989-758-774-0

female populations (Carlsson, Hammar, & Gril,

2005). In addition, studies have shown that high

triglyceride levels are an independent risk factor for

diabetes mellitus, especially significant in young men

(Tirosh et al., 2008).

Dietary composition has a profound effect on

diabetes. Studies in India have shown that high sugar

intake is strongly associated with increasing trends in

obesity and type 2 diabetes, affecting metabolism

mainly through insulin resistance and fat

accumulation (Gulati & Misra, 2014). Despite

medical advances that have reduced some of the risks

of diabetic complications, the prevalence of diabetes

is still rising globally, and the burden of disease is

expected to increase further with an ageing

population and increasing obesity rates (Deshpande,

Harris-Hayes & Schootman, 2008).

According to over studies, in order to provide a

more comprehensive diabetes prevention and control

strategy, this study aims to analyze a dataset to

investigate the various factors influencing diabetes

and the internal relations between these factors with

the logistic regression (LR) model and the random

forest (RF) model.

2 METHODOLOGY

2.1 Data Source and Description

The dataset used in this study is the Pima Indians

Diabetes Database, a widely used dataset for diabetes

prediction and related research. The data was

originally collected by the National Institute of

Diabetes and Digestive and Kidney Diseases

(NIDDK) and contains diagnostic information on

Pima Indian women aged 21 years and older (Kaggle,

n.d.). This dataset consists of 768 observations with 9

variables, including Pregnancies (PREG), Glucose

(GLUC), Blood Pressure (BLDP), Skin Thickness

(SKIN), Insulin (INSU), Body Mass Index (BMI),

Diabetes Pedigree Function (DPF), Age, and

Outcome. Among these variables, the Outcome

stands for whether the patient is diagnosed with

diabetes, and it stays with binary form where 1

indicates a diagnosis of diabetes and 0 indicates no

diagnosis.

The dataset has been preprocessed to remove

missing values and ensure consistency across all

observations. Each variable represents different

health-related indicators that are commonly used in

diabetes research. The dataset is publicly available

and widely used in medical and machine learning

studies to explore diabetes risk factors.

2.2 Selection and Explanation of

Variables

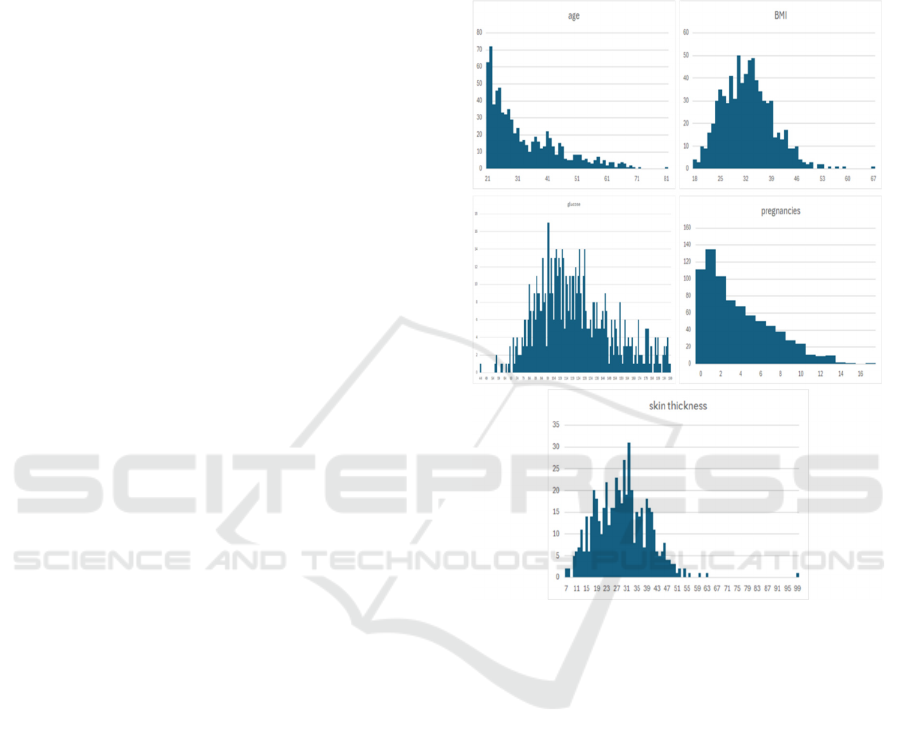
As shown in Figure 1, this study focuses on these key

variables, including age, BMI, BLDP, DPF, GLUC,

INSU, PREG, SKIN:

Figure 1: Distribution of Variables

(Photo/Picture credit:

Original).

2.3 Model Choice

The dataset will be used to fit in a LR model because

it is interpretable, has probabilistic outputs, and is

consistent with the research goal of understanding

diabetes risk factors. Unlike complex machine

learning models, LR provides clear and interpretable

coefficients that allow researchers and healthcare

professionals to understand how each predictor (e.g.,

blood glucose level, BMI, age, and family history)

affects the likelihood of developing diabetes.

Moreover, LR can naturally handle binary

classification problems, such as diabetes prediction,

where the outcome is either diabetes (1) or non-

diabetes (0). LR model is also suitable for fields that

need analysis of the importance of features, such as

medication. The model estimates the probability of

diabetes occurring, making it suitable for risk

assessment and threshold-based medical decision-

Diabetes Risk Assessment: A Logistic Regression Modelling Study Based on Large-Scale Data

465

making. The resulting advantage ratios help quantify

the impact of individual predictors, which is useful

for both clinical guidelines and public health policy.

RF model will also be employed to complement

the findings of the LR model. While LR is well-suited

to understanding the linear relationship between risk

factors and diabetes, RFs help to address non-linear

interactions and complex dependencies between

variables, providing a broader perspective on the

factors that influence diabetes.

3 DATA ANALYSIS OUTCOME

3.1 LR Model

Table 1 is the LR model output

Table 1: Output of LR Model

Estimate

Std.Erro

z value

Pr(>|z|

)

(Intercept

)

-8.405 0.717

11.728

0.000

0.123 0.032 3.840 0.000

gluc

0.03

0.004 9.481 0.000

-0.013 0.005 -2.540 0.011

skin 0.001 0.007 0.090 0.928

insu -0.001 0.001 -1.322 0.186

mi 0.090 0.015 5.945 0.000

dia_p 0.945 0.299 3.160 0.001

e 0.015 0.009 1.593 0.111

The analysis of the dataset through a LR model

demonstrates how various variables produce

statistically relevant effects on diabetes prediction.

The data reveals that both pregnancies and glucose

and BMI measurements, together with diabetes

prediction, perform as the highest significant positive

influential factors in the model. Among them, glucose

shows the strongest statistical significance, followed

by BMI, while pregnancies and diabetes prediction

play supporting roles. The results proved compatible

with existing medical knowledge regarding the risk

factors of diabetes, which include elevated glucose

levels, together with higher BMI and an inherited

history of diabetes. This model indicates that blood

pressure shows slight statistical significance, yet

insulin levels and age, together with skin condition,

exhibit no substantial evidence of contributing to

diabetes prediction.

The model’s overall performance was evaluated

using the Akaike Information Criterion (AIC), which

yielded a value of 741.45, indicating a reasonable

model fit. Meanwhile, the model’s predictive

accuracy has reached 78.26%, which also indicates

the great quality of the model.

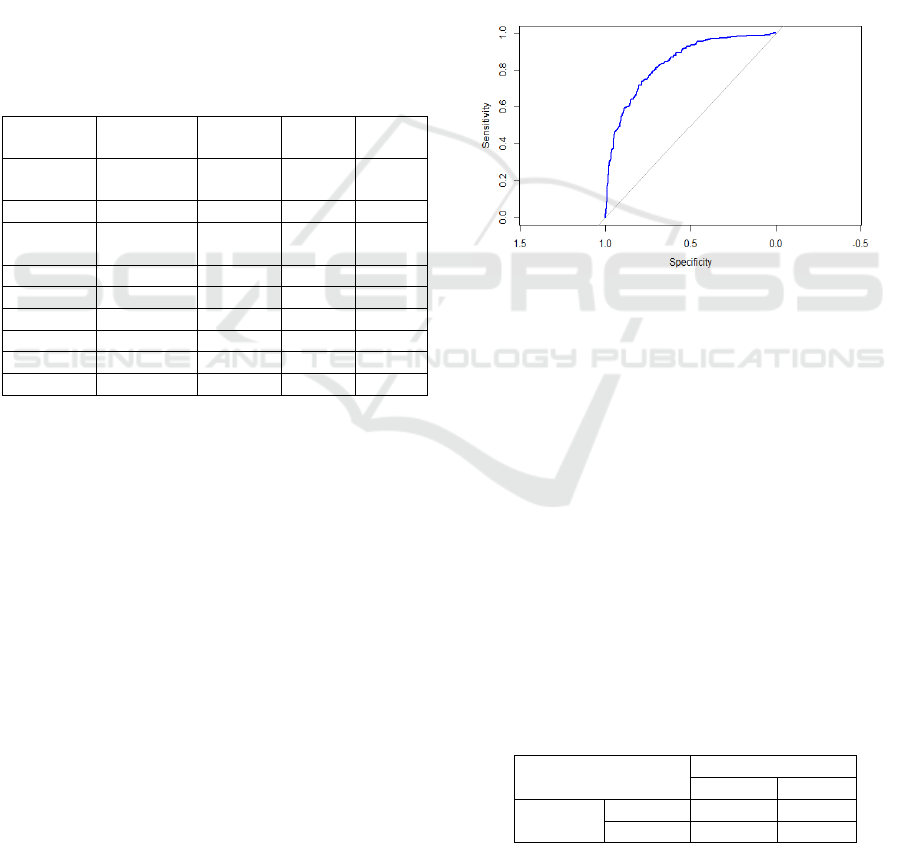
In addition, the Receiver Operating Characteristic

(ROC) curve is also generated with its Area Under

Curve (AUC) value to evaluate such a model, and

generally, a model with strong discriminatory power

will have a curve that rises sharply towards the upper-

left corner, indicating high sensitivity and specificity.

In this case, as seen in Figure 2, the ROC curve is

well above the diagonal reference line, which

represents a model making random guesses indicating

that the LR model performs significantly better than

random classification. Meanwhile, the value of AUC

reaches 0.8394. Both results demonstrate that the LR

model is effective in predicting diabetes status.

Figure 2: ROC Curve of LR Model (Photo/Picture credit:

Original).

3.2 RF Model

The RF model is used on the diabetes dataset for

comparison with the previously analyzed LR model.

This model implementation utilizes 500 different

decision trees that randomly choose 3 variables from

the tree variables for each splitting operation. The

entire data collection underwent partitioning into

testing with 30% and training with 70%. The out-of-

bag error rate reached 25.14%, which represents a

good classification outcome. The accuracy level in

testing reached 74.03%, which proved that the model

performed well yet required improvements.

The confusion matrix of the RF is shown in Table

Table 2: Confusion Matrix of RF

Actual

Negative Positive

Predicte

Negative 126 36

Positive 24 45

RF feature importance as Table 3.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

466

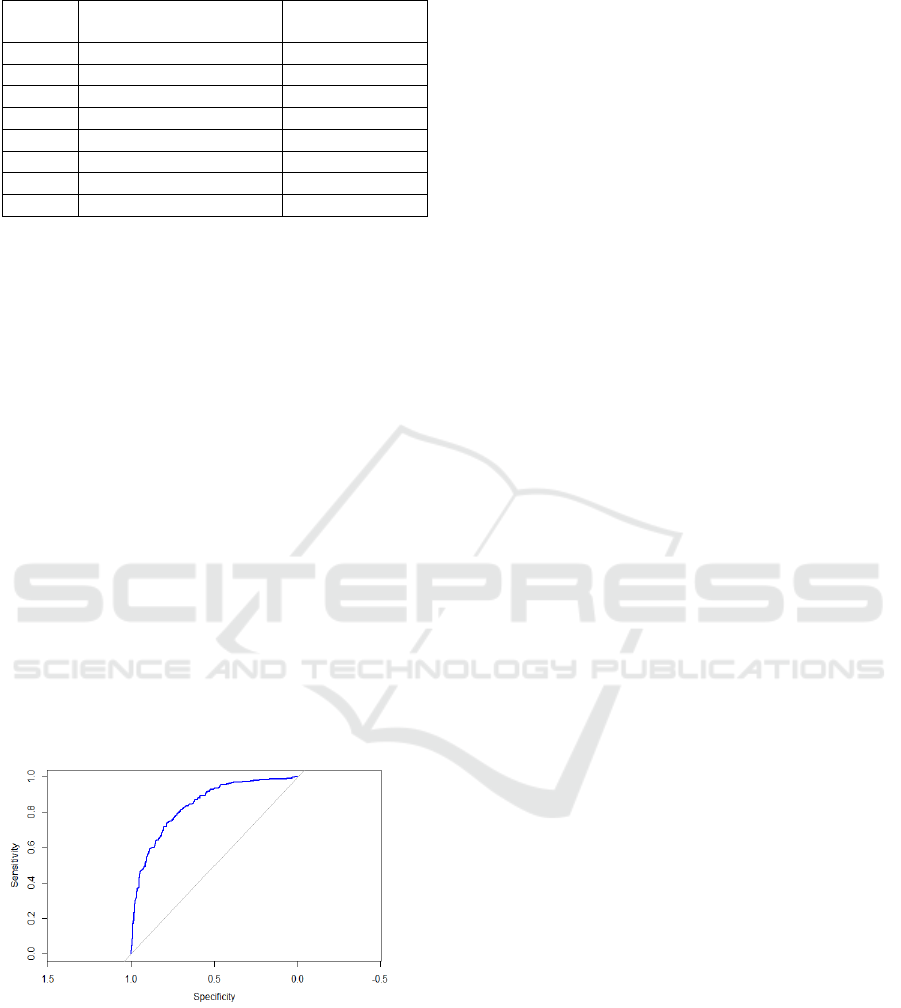
Table 3: RF Feature Importance

Feature

Mean Decrease

Accurac

Mean Decrease

Gini

gluc 42.54 69.6

mi 22.95 43.46

e 12.57 29.03

dia

9.52 29.52

8.21 17.99

ldp 1.77 21.52

skin 3.78 16.1

insu 3.76 15.75

The RF model demonstrates that glucose and BMI,

along with age act as the prime predictors of disease

status because these variables match medical

consensus. The established models underline the

value of glucose measurements and Body Mass Index

tests for predicting diabetes outcomes, although they

exhibit various approaches in managing age detection

and pregnancy status.

Both models include skin and insulin as

predictors, which do not substantially influence the

prediction of diabetes status. The confusion matrix

showed the model successfully identified most non-

diabetic cases, but demonstrated poor accuracy in

detecting diabetes patients by mistakenly identifying

some diabetic patients as non-diabetic.

To further evaluate model performance, the ROC

curve was plotted, and the AUC reached 0.831

(Figure 3). This suggests that the RF model had

strong discriminatory power, indicating considered

indicative of good classification performance. The

curve demonstrates that the model performs

significantly better than random guessing, which

means that the model performs effectively.

Figure 3: ROC Curve of RF (Photo/Picture credit:

Original).

LR is particularly advantageous in binary

classification tasks like diabetes prediction due to its

probabilistic interpretation and inherent

interpretability. By modeling the log-odds of diabetes

occurrence, it provides clinicians with a

straightforward metric—for instance, a 1.5-fold

increase in odds per 10 mg/dL rise in glucose levels

(OR=1.5, p<0.01)—to quantify risk thresholds for

intervention. This aligns with clinical workflows

where actionable thresholds (e.g., HbA1c ≥6.5%)

guide diagnoses. Furthermore, its coefficients

directly inform evidence-based guidelines; for

example, public health campaigns could prioritize

BMI reduction if the model identifies it as a high-

impact variable (OR=1.3). However, its reliance on

linearity assumptions may oversimplify interactions,

such as age-dependent glucose metabolism variations,

necessitating complementary non-linear models.

The RF model complements LR by capturing non-

linear relationships and higher-order interactions

obscured in parametric frameworks. For example, it

might reveal that the combined effect of elevated

BMI and age over 50 amplifies diabetes risk

disproportionately—a pattern LR could miss. Its

ensemble structure, leveraging bootstrap aggregation

and feature randomness, also mitigates overfitting,

enhancing robustness in noisy clinical data. By

ranking variables via mean decrease in Gini impurity,

it identifies context-dependent predictors, such as

pregnancy-triggered insulin resistance in specific

BMI subgroups. While less interpretable than LR, its

ability to model complex dependencies (e.g., time-

varying glucose-insulin dynamics) offers nuanced

insights for personalized prevention strategies,

bridging gaps in traditional statistical approaches.

4 DISCUSSION

The results of this study provide valuable insights into

the predictive factors associated with diabetes and the

comparative performance of LR and RF models in

clinical risk assessment. Both models demonstrated

strong predictive capabilities, with LR achieving an

accuracy of 78.25%, slightly outperforming the RF

model (74.03%). This marginal difference may stem

from their distinct methodological frameworks: LR,

as a parametric model, excels in capturing linear

relationships between variables, while RF, a non-

parametric ensemble method, prioritizes complex

interactions and non-linear patterns. Despite this

divergence, both models consistently identified

glucose level and BMI as the most critical predictors

of diabetes.

This aligns with established clinical knowledge,

as elevated glucose levels directly reflect impaired

insulin function, while higher BMI values correlate

with visceral adiposity and metabolic dysfunction,

both hallmarks of diabetes pathophysiology.

Divergent interpretations emerged for age and

Diabetes Risk Assessment: A Logistic Regression Modelling Study Based on Large-Scale Data

467

pregnancy history. LR assigned these variables

moderate importance (e.g., age odds ratio: 1.15,

p=0.02), suggesting cumulative metabolic wear or

hormonal shifts over time. In contrast, RF

downplayed their significance, possibly because

interactions between age and other variables (e.g.,

age-specific glucose thresholds) were overshadowed

by stronger predictors like BMI. This discrepancy

underscores the importance of model selection: LR’s

interpretability aids hypothesis testing (e.g., age as an

independent risk factor), while RF’s flexibility may

better reflect multifactorial risk profiles in

heterogeneous populations. Both models agreed on

the limited predictive value of skinfold thickness and

insulin levels. Skinfold thickness, a proxy for

subcutaneous fat, may lack specificity compared to

BMI, which encompasses visceral fat, a more direct

contributor to insulin resistance. Similarly, insulin

levels alone might fail to capture dynamic feedback

mechanisms (e.g., pancreatic β-cell compensation)

critical in early diabetes stages. These findings

suggest that simplified biomarkers (glucose, BMI)

hold greater utility in screening protocols compared

to niche measurements. The complementary strengths

of LR and RF advocate for their combined use in

clinical practice. For instance, LR could prioritize

high-risk patients based on glucose/BMI thresholds,

while RF might refine predictions by incorporating

subtle interaction effects (e.g., age-adjusted BMI

thresholds). Such integration could enhance

personalized prevention strategies, enabling early

interventions like lifestyle modifications or targeted

glucose monitoring. Future studies should validate

these models across diverse populations and explore

hybrid algorithms to balance interpretability and

predictive power (Zimmet et al., 2014).

5 CONCLUSION

The findings of this study, while insightful, are

inherently constrained by the demographic

homogeneity of the dataset. All observations were

derived exclusively from female Pima Indians aged

21 and older, a population with a well-documented

genetic predisposition to metabolic disorders. While

this homogeneity reduces confounding variables, it

severely limits the generalizability of the models. For

instance, biological differences across gender and

racial/ethnic variations in diabetes risk factors may

render the current models inapplicable to broader

populations. Future research must prioritize

ethnically diverse cohorts—including Asian, African,

and European ancestries—and balanced gender

representation to validate and refine these predictive

frameworks. Methodologically, advancements could

be achieved through feature engineering, ensemble

techniques, or deep learning architectures.

Additionally, addressing the dataset’s class

imbalance—a common issue in medical datasets

where non-diabetic cases dominate—using

techniques like SMOTE or cost-sensitive learning

could reduce prediction bias. Integrating real-world

clinical variables, such as dietary habits, physical

activity metrics, and polygenic risk scores, would

further bridge the gap between algorithmic

predictions and clinical utility. For example, wearable

device data could dynamically update risk

assessments based on lifestyle changes. Finally,

ethical considerations around data privacy and model

transparency must accompany technical

improvements. By adopting these strategies, future

studies can develop robust, equitable tools for

diabetes prevention, ultimately supporting

personalized healthcare interventions across diverse

global populations.

ACKNOWLEDGEMENTS

All the authors contributed equally and their names

were listed in alphabetical order.

REFERENCES

Carlsson, S., Hammar, N., & Grill, V., 2005. Alcohol

consumption and type 2 diabetes: Meta-analysis of

epidemiological studies indicates a U-shaped

relationship. Diabetologia, 48, 1051–1054.

De Luis, D. A., Fernandez, N., Arranz, M. L., Aller, R.,

Izaola, O., & Romero, E., 2005. Total homocysteine

levels relation with chronic complications of diabetes,

body composition, and other cardiovascular risk factors

in a population of patients with diabetes mellitus type 2.

Journal of Diabetes and its Complications, 19(1), 42–

46.

Dehghan, A., Kardys, I., de Maat, M. P., Uitterlinden, A.

G., Sijbrands, E. J., Bootsma, A. H., ... & Witteman, J.

C., 2007. Genetic variation, C-reactive protein levels,

and incidence of diabetes. Diabetes, 56(3), 872–878.

Deshpande, A. D., Harris-Hayes, M., & Schootman, M.,

2008. Epidemiology of diabetes and diabetes-related

complications. Physical Therapy, 88(11), 1254–1264.

Gale, E. A., & Gillespie, K. M., 2001. Diabetes and gender.

Diabetologia, 44, 3–15.

Gulati, S., & Misra, A., 2014. Sugar intake, obesity, and

diabetes in India. Nutrients, 6(12), 5955–5974.

Kaggle Datasets, n.d. Pima Indians Diabetes Database.

Available at:

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

468

https://www.kaggle.com/datasets/uciml/pima-indians-

diabetes-database

Roglic, G., 2016. WHO Global report on diabetes: A

summary. International Journal of Noncommunicable

Diseases, 1(1), 3–8.

Tirosh, A., Shai, I., Bitzur, R., Kochba, I., Tekes-Manova,

D., Israeli, E., ... & Rudich, A., 2008. Changes in

triglyceride levels over time and risk of type 2 diabetes

in young men. Diabetes Care, 31(10), 2032–2037.

Zimmet, P. Z., Magliano, D. J., Herman, W. H., & Shaw, J.

E., 2014. Diabetes: A 21st century challenge. The

Lancet Diabetes & Endocrinology, 2(1), 56–64.

Diabetes Risk Assessment: A Logistic Regression Modelling Study Based on Large-Scale Data

469