
Enhancing Resilience of Strong Structural Controllability in
Leader-Follower Networks
Vincent Schmidtke
a
and Olaf Stursberg
b
Control and System Theory, EECS Dept., University of Kassel, Germany
Keywords:
Strong Structural Controllability, Leader-Follower Networks, Edge Augmentation, Resilient Control.
Abstract:
This paper explores measures of edge augmentation to enhance resilience of strong structural controllability
for control systems modeled as leader-follower networks. Unlike existing methods which typically increase the
number of leaders, the proposed approach achieves resilience by strategically adding edges, thus maintaining
leader sets with a small cardinality. Using the zero forcing method, conditions are derived to enhance resil ience
either for specific agents or for the entire network. Numeric simulations validate the approach and show its
effectiveness in large and complex networks.
1 INTRODUCTION
Networked Control Systems (NCS) are integral to
modern engineering, enabling distributed coordina-
tion and scalability in complex systems such as smart
grids, traffic systems, swarms and biological net-
works. In these systems, it is frequently desired to
control the network by injecting control actions only
for a small subset of nodes. This leads to the notion
of leader-follower frameworks, where leaders have a
control input, whereas followers do not h ave one (Por-
firi and di Bernardo, 2008; Egerstedt et al., 2012).
While this can simplify the con trol architectur e, the
system may g et more fr a gile with respect to malfunc -
tions or attacks, if the loss of an agent and/or its co n-
nections significantly impairs the system’s functio n-
ality (Pasqualetti et al., 2020).
Controllability and resilience are thus important
properties when investigating in how far such systems
can maintain their function if subject to internal or
externally triggere d changes. Controllability ensure s
the ability to let the system transition from any ini-
tial state to a desired state, while resilience pertains to
the system’s capacity to withstand (or recover from)
disruptions. These properties are c rucial, especially
in safety-critical applications where failures can have
catastrophic co nsequences.
This paper focuses on the notion of strong struc-
tural controllability (SSC) which requires controlla-
bility for varying inte rconnections of states (and thus
structures) of the system to be con trolled. This is par-
a
https://orcid.org/0009-0006-6322-103X
b
https://orcid.org/0000-0002-9600-457X
ticularly advantageous in NCS, since controllability
depends on the network topology and the leader set,
rather than only particular weights assigned to con-
stantly existing interconnections. This makes SSC
suitable for real-world applications, in which infor-
mation on ed ge weights may be uncertain, time-
varying, noisy, or even vanishing (Ch apman and Mes-
bahi, 2013; Monshizad e h et al., 2014).
In order to assess SSC of leader-follower networks
as well as its resilience against changing network
topologies, this paper utilizes the m ethod of zero forc -
ing sets, a graph -theoretic appro ach that is frequently
used in the context of SSC for NCSs (Monshizadeh
et al., 2014; Abbas et al., 2020b; Schmidtke et al.,
2024). In the context of SSC, the following exist-
ing papers have proposed edge augmentation, i.e. the
addition of edges to a graph, as a means to modify
the system structure for enhanced contr ollability. In
(Chen et al., 2019), minimal edge sets are computed
to render non-SSC system s structura lly controllable,
whereas (Abbas et al., 2020a) and (Mousavi et al.,
2021) identify a set of edges that can be added without
violating SSC. These approaches leverage e dge aug-
mentation as a design tool to either restore or preserve
controllability.
A certain body of literature in the given con-
text has examined the relationship between graph-
theoretic robustness measur e s and the minimum num-
ber of required leaders: The m ost often used mea-
sure is the Kir choff index, which formulates the sys-
tem’s resilience against disconnection. (Pasqualetti
et al., 2020) and (Abbas et al., 2020b) investigate the
trade-off between an increasing connectivity and the
minimum number of required leader agents, which is
136
Schmidtke, V. and Stursberg, O.
Enhancing Resilience of Strong Structural Controllability in Leader-Follower Networks.
DOI: 10.5220/0013826200003982
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 136-144
ISBN: 978-989-758-770-2; ISSN: 2184-2809
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

also discussed as a central controllability measure in
(Egerstedt et al., 2012). T he work in (Abbas e t al.,
2024) identifies edge additions leading to a reduction
of th e required number of leader agents, while in-
creasing the robustness measure. A design pr ocedure
which builds a graph which is SSC with the highest
possible Kirc hoff ind ex for specified graph parame-
ters is presen te d in (Patel et al., 2024).
The notion of robustness addressed in the afore-
mentioned work differs from the approach to r e -
silience taken in this pap er. Rather than focusing
on graph connectivity, resilience of controllability is
here specifically considered with re spect to preserv-
ing SSC in case of structur a l d isruptions such as node
or edge failures. Resilient SSC is addressed only in
very few contributions: In (Schmidtke et al., 2024),
conditions have been specified which allow to check
which agents can be removed from the system, while
maintaining SSC with the cur rent leader set. T he pa-
pers (Abbas, 2023) and (Alameda et al., 2024) exploit
methods to specify a set of lea der agents which guar-
antees that a certain number of nodes or edges c an be
removed, while keeping the system SSC. However,
these methods require the introduction of far more
leader ag ents – this, on the one hand, leads to leader
selection p roblems which are known to be NP-hard in
general (Aazami, 2008). On the other hand, this ap-
proach contradicts the goal to have as few leaders as
possible. Thus overall, a significant gap in literature is
the enha ncement of resilience without incre a sing the
number of leader ag ents. This paper addresses this
gap by proposing schemes to augment the graph by
additional edges in order to achieve strong structural
controllability, including the case that agents leave
and/or join the network.
The paper is structured as follows: Section 2 intro-
duces preliminaries on th e system class, the property
of stron g structural controllability, and the zero fo rc-
ing method. Section 3 f ormally states the problem
of en hancing resilien t strong struc tural controllability
through modifying the edges of the graph. Section 4
presents the main results, while Section 5 provides a
numeric example to illustrate the approach. Finally,
Section 6 concludes the p aper, summ arizing th e find-
ings and their implications.
2 PRELIMINARIES
Networks are in this paper represented by a graph
˜
G = (V ,E,W ), in which V = {1,...,N} is the set of
agents, E the set of edge s, and W the set of weights
assigned to each e dge according to w
i j
: E → R \ 0.
For simp lification, it is assumed that (i, j) ∈ E ⇔
( j, i) ∈ E, which simplifies the notation. However,
w
i j
6= w
ji
is allowed, making th e graph direc te d. It
is im portant to note, that the upcoming results can
be straightforwardly extended to cases where the as-
sumption of bi-directional edges is dropped. Edges
(i,i) for represen ting self-loops are permitted. Let all
neighbors of a node i be collected in a set N
i
= { j ∈
V |( j,i) ∈ E, j 6= i}.
The set of agents is divided into a set of leader
agents V
l
= {l
1
,. .. ,l
m
l
} ⊆ V and the set of follower
agents V \ V
l
. The m
l
leaders have a control input
u
i
(t) and the dynamics:
˙x
i
(t) = w
ii
· x
i
(t) +
∑
j∈N
i
w
i j
· x
j
(t) + u
i
(t), (1)
while the dynamics of the followers:
˙x
i
(t) = w
ii
· x
i
(t) +
∑
j∈N
i
w
i j
· x
j
(t) (2)
lacks an input. Note that with this definition the lead-
ers ar e allowed to interact dy namically with follower
and leader agents. The in itial state of any agent is de-
noted by x
i
(0) = x
i,0
.
The glob a l dynamics of all ag ents can be
derived b y introducing the state vector x(t) :=
[x
T
1
(t),x
T
2
(t),... ,x
T
N
(t)]
T
∈ R
N
, the input vector
u(t) := [u
T
1
(t),u
T
2
(t),... ,u
T
m
l
]
T
∈ R
m
l
, the weight ma-
trix W with elements w
i j
, and the leader selection ma-
trix B ∈ [0 , 1]
N×m
l
accordin g to:
B =
(
b
i j
= 1 if i = l
j
0 otherwise.
(3)
The g lobal dynamics of the network ca n then by writ-
ten as:
˙x(t) = W x(t) + Bu(t), (4)
in which the leader agents can be controlled, whereas
the follower agents only respond to the beh avior of
the leader agen ts.
2.1 Strong Structural Controllability
As is well known, a system (4) is controllable if the
following matrix has full rank (Antsaklis and Michel,
1997):
R(W,B) =
B W B .. . W
n−1
B
, (5)
In networked systems, however, edge weights are of-
ten either unavailable or time-varying, rendering the
direct use of (5) impractical. T hen, strong structural
controllability (SSC) becomes relevant, as it assesses
controllability sole ly based on the system’s structu re,
indepen dent of the specific edge weights. To define
Enhancing Resilience of Strong Structural Controllability in Leader-Follower Networks
137
SSC, the following family of matrices associated with
a given graph
˜
G is conside red:
W (
˜
G) = {W ∈ R
N×N
: for i 6= j, w
i j
6= 0 ⇔ ( j, i) ∈ E}.
(6)
This matrix family includes all matric e s for which
the nonzero off-diagonal entries corre spond exactly
to the edges of
˜
G. Note that the d ia gonal elements of
every W ∈ W (
˜
G) can be arbitrary. With this notation,
SSC can be defined as follows:
Def. 1 (Strong Structural Contro llability). A linear
system according to (4) is SSC if and only if the pair
(W,B) is controllable for all W ∈ W (
˜
G), where B rep-
resents the agents through which inputs are applied.
Aiming at SSC according to this definition re-
quires that any possible matrix W of the given dimen-
sion needs to be considered, while the zero e ntries W
are encod ed also by the fact that a corre sponding edge
is not de fined in E. Thus, it is sufficient (without loss
of generality) from here on to refer the considerations
on SSC to a reduced version G = (V ,E) of the graph
˜
G without weights.
2.2 SSC and Zero Forcing
The use of zero forcing as a method to examine SSC
is motivated by its direct co rrelation to network con-
trollability on graphs, as explained in (Monshizadeh
et al., 2014), see also Th e orem 1. Zero forcing is
defined as follows (AIM Minimum Rank - Special
Graphs Work Group, 2008):
Def. 2 (Zero Forcin g). For a graph G = (V ,E), let
V
c
0
⊂ V , |V
c
0
| > 0 be chosen arbitrarily as an initia l
set of colored nodes. Let then V be partitioned into
V
c
0
and a set V
u
0
of initially uncolored nodes accord-
ing to V
c
0
∩ V
u
0
= ∅ and V
c
0
∪ V
u
0
= V . If a colored
node i then only has one uncolored neigh bor j, the n j
is forced to be colored by i (denoted by i ⇀ j), i.e. j
is inserted into V
c
and removed from V
u
. This color-
ing p rocess continues until n o further coloring can be
executed, leading to final colored and uncolored sets
V
c
f
and V
u
f
.
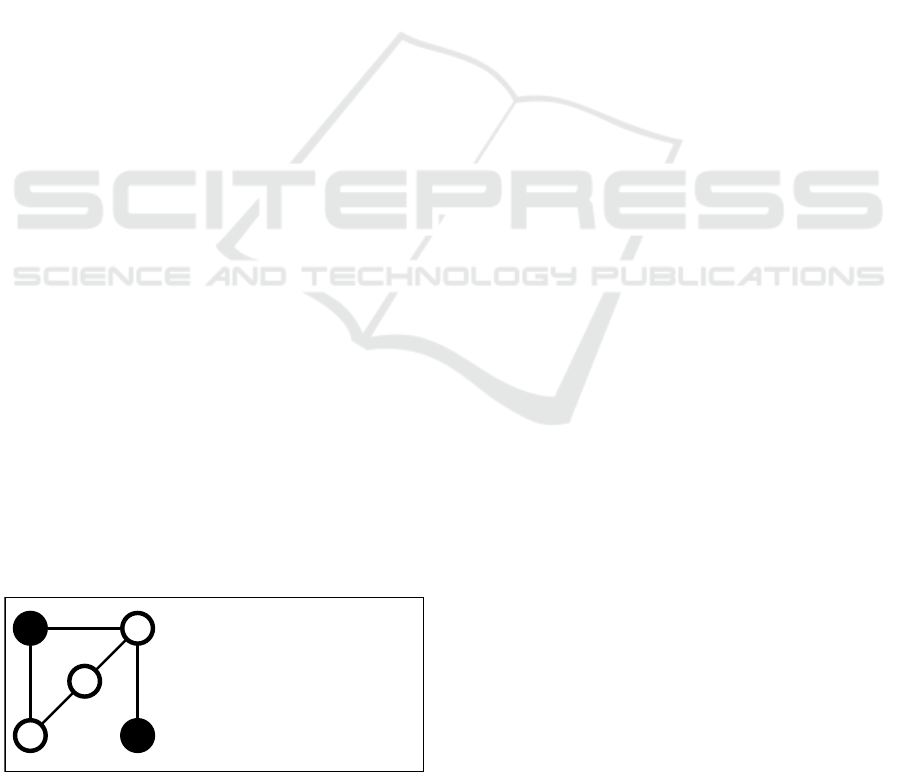
1 2
3
4
5
G
V
c
0
= {1,4}
C
1
(G,V
c
0
) = {4 ⇀ 2,1 ⇀ 3,3 ⇀ 5}
C
2
(G,V
c
0
) = {4 ⇀ 2,2 ⇀ 5,5 ⇀ 3}
D(G,V
c
0
) = V
F
5
(G,V
c
0
) = {2, 3}
Figure 1: Example for zero forcing with V
c
0
as ZFS with
minimal cardinality.
Def. 3 (Derived Set). If zero fo rcing has started from
V
c
0
and terminated with V
c
f
, the latter set is also
called th e derived set and is denoted by D(G,V
c
0
) :=
V
c
f
.
Def. 4 (Zero Forcing Set). If a selected set of initially
colored n odes V
c
0
leads to D(G, V
c
0
) = V (i.e. all
nodes are colored at the end of zero forcing), V
c
0
is
called zero forcing set (ZFS) .
In ad dition the following terms are intr oduced:
Def. 5 (Forcing Chain). A forcing chain (FC)
C (G,V
c
0
) contains the list of forces i ⇀ j obta ined
during zero forcing for the graph G, where this list is
sorted according to th e sequence of forces carried out
during the forc ing procedure when starting from V
c
0
.
Def. 6 (Forcing Agen ts). For an agent j ∈ V , the
set F
j
(G,V
c
0
) contains all forcing agents (FA) i ∈ V ,
which can color j throu gh a force i ⇀ j con tained in
any fo rcing chain C (G,V
c
0
).
An example that illustrates these quantities can
be found in Fig. 1. As shown there, forcing chains
generally lack uniqueness, while the derived set
D(G,V
c
0
) remains unique ( A IM Minimum Rank -
Special Graphs Work Group, 2008). For any set of
FA, the inequality |F
j
(G,V
c
0
)| ≤ |N
j
| is always sat-
isfied beca use only neighbors are capable of color-
ing an agent. When V
c
0
constitutes a ZFS, it en-
sures that |F
j
(G,V
c
0
)| ≥ 1 for all j ∈ V
u
0
, guarantee-
ing that at least one FC for every u ncolored agent ex-
ists. Accordingly, |F
j
(G,V
c
0
, j)| = 0 for all j ∈ V
c
0
since these agen ts are colored initially.
The following theorem from (Monsh iz adeh et al.,
2014) establishes that zero forcing can determ ine if
a leader set V
l
guaran tees strong structu ral controlla-
bility fo r the system defined by the graph G:
Theorem 1 ((M onshizadeh et al., 20 14)). System (4)
with W ∈ W and B defined by the leade r set V
l
is SSC
if and only if V
l
is a ZFS for G.
2.3 Resilient SSC
In network controllability, resilience refers to the sys-
tem’s ability to remain controllab le despite agent mal-
functions or edge failures (Abbas, 2023). In terms of
structural controllability, the concept of a ZFS is ex-
tended to l-le aky forcin g sets, defined as follows:
Def. 7 (l-Leaky Forcing Set). The leader set V
l
is a l−leaky forcing set (l−LFS), if ∀i ∈ V \ V
l
:
F
i
(G,V
l
) ≥ l + 1.
Building on the previous definition, (Abbas, 2023)
demonstra te s that an l-LFS provides resilience ag a inst
l malfunctions, where a malfunction m ay involve a
node departure or edge removal. ( N ote that the case
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
138
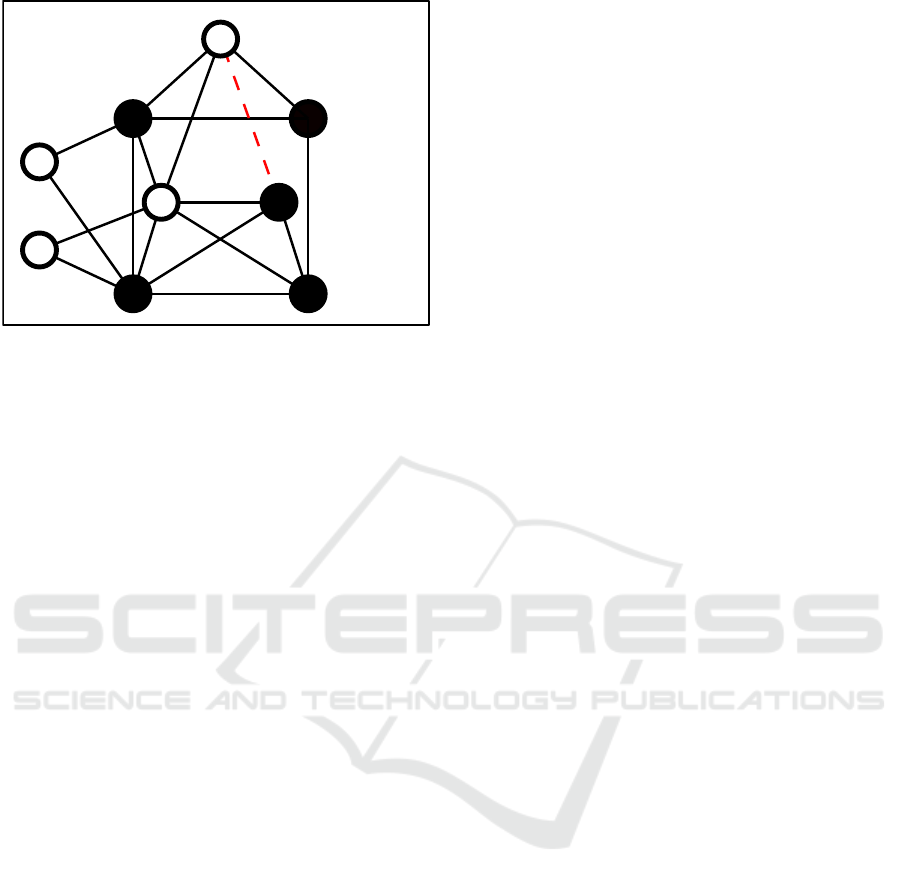
12
3
4
5
6
7
8
9
F
5
(G,V
l
) = {1}
F
5
(G
′
,V
l
) = {1; 4}
Figure 2: In graph G, node 1 has only node 5 as its only one
forcing agent, i.e., the system is no longer SSC if node 1 is
removed from the graph. In G
′
, which is obtained by adding
the edge indicated by the red dashed line to G, node 5 has
an additional forcing agent, and therefore the graph remains
SSC, if node 1 i s removed.
of entering agents is not considered here, but results
on this situation can be found in (Schmidtke et al.,
2024).
3 PROBLEM STATEMENT
While in (Abbas, 2023) the l-LFS guarantees re-
silient SSC by introducing additional leader agents,
the present work aims at improving resilience through
edge augmentation, i.e., by adding new edges to the
graph.
Formally, given a gra ph G = (V ,E ) with a ZFS
V
l
, the addressed problem is to enhance resilience by
adding an edge (i, j) (where i, j ∈ V and (i, j) 6∈ E)
such that:
|F
i
(G,V
l
)| < |F
i
(G
′
,V
l
)|, (7)
for G
′
= (V ,E ∪ (i, j )).
This approach, which can be applied iteratively,
follows the principle of the l-LFS methodology by in-
creasing the n umber of FA for critical nodes. How-
ever, this is ach ieved through the addition of edges
rather th an by expanding the leader set. The method
is par ticularly well-su ited for scena rios in whic h bot-
tlenecks or vulnerable regions of the network ar e
known in advance. In such cases, edge augmenta-
tion can be applied in a targeted manner to strengthen
the resilience of specific nodes, thereby improving
resilience without the need to intr oduce additional
leader agents.
For instance, in scenarios like the one in Fig. 2,
resilience is ensured by leveraging the result from
(Schmidtke et al., 2024): SSC is preserved, when
an agent j leaves G, provided that for all uncolored
neighbors i ∈ N
j
the following holds:
|F
i
(G,V
l
) \ j| > 0. (8)
To date, no publishe d meth od systematically explores
possibilities of modifyin g the set of FA through leader
selection or edge augmentation. Thus, the following
section proposes a framework for strategically mod-
ifying the network topology to enhance resilience of
SSC.
4 IMPROVING RESILIENCE BY
EDGE AUGMENTATION
The primary objective o f this section is to establish
conditions that guarantee (at least loca lly) enhanced
resilience of SSC by augmentin g the set E of the
graph G by an additional edge (i, j). To ac hieve this,
the no tion of a forcing graph is introduced. The latter
enables the analysis o f the forcing agents of G by
examining how the addition of the edge affects the
network’s resilience. Based on this analysis, a main
theorem is formulated stating conditions under which
the augmentation leads to improved resilience. Fur-
thermor e, this section shows that, under the derived
conditions, a ZFS in G retains the SSC properties,
ensuring that resilience is either glo bally or locally
enhanced.
A forcing graph is introduced to determine whic h
nodes are c olored before a specific uncolored n ode,
under the conditio n that a designated co lored node
does not color any o ther node. The formal definition
is as follows:
Def. 8. Give n a graph G = (V ,E), let i ∈ V
u
be an
uncolored node and j ∈ V
c
a colored node. A forc-
ing graph
¯
G
i j
= (
¯
V ,
¯
E) is constructed by in troducin g
two dummy nodes, α and β, thus
¯
V = {V ∪ {α; β}} ,
and a modified set of edges is obtained from
¯
E =
{E ∪ {(α,l) | l ∈ N
i
} ∪ {(α, j),(β, j)}}. In here, α
is connected to all neighbors of i and to j, while β is
only connected to j.
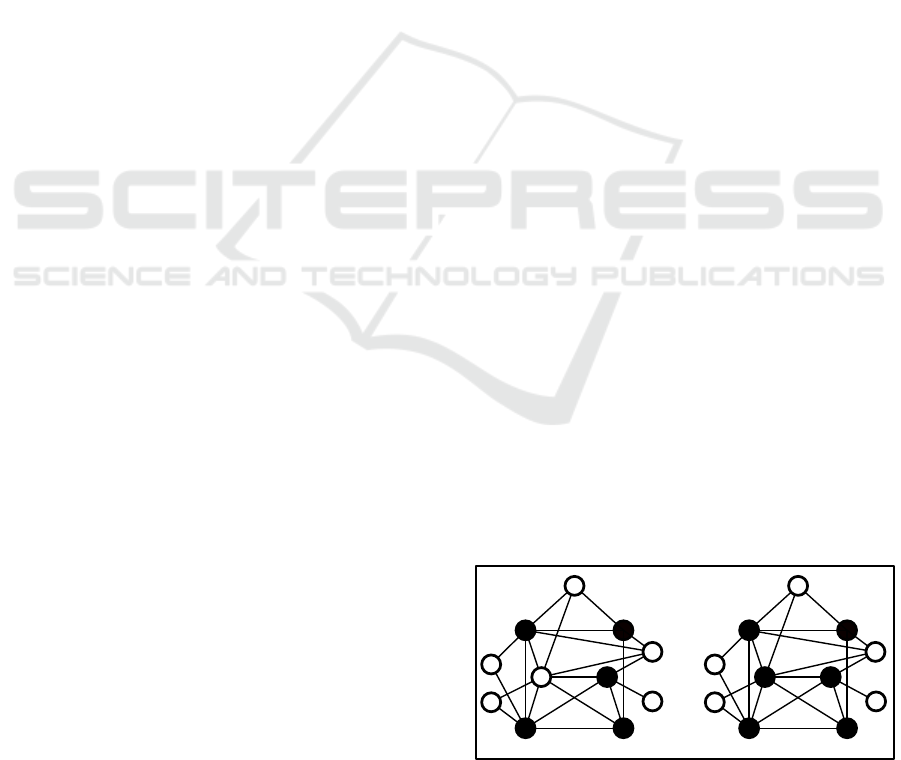
An example of a forcing gra ph is shown on the
left h and side of Fig. 3, where the graph from Fig. 2
is expanded by the nodes i = 5 and j = 4.
Note that the forcing graph is a direct extension of
the extended graph, introduced in (Schmidtke et al.,
2024), w hich is denoted in this paper by
¯
G
i{}
. In
this extende d graph, which can be used to determine
the FA of node i over all FC (see (Schmidtke et al. ,
Enhancing Resilience of Strong Structural Controllability in Leader-Follower Networks
139
2024)), the node α is only connected to the neighbors
of i, and β has no neighbors.
The following result can be obtained for the de-
rived set of the forcing graph:
Lemma 1. Using a ZFS V
l,1
for G, the following con-
dition holds true for the forcing process on the forcing
graph
¯
G
i j
for every p air (i, j) with i ∈ V
u
, j ∈ V
c
:
{α,β,i} 6∈ D(
¯
G
i j
,V
l,1
). (9)
Proof. Based on the definition o f
¯
G
i j
, it follows
that N
i
⊂ N
α
. Consequently, node i can only b e
colored after node α has been colored. Given that
N
α
\ N
i
= { j}, node j is the only node being able to
color α. Furthermore, due to the construction of
¯
G
i j
,
the condition N
β
= { j} always holds. Neither α nor
β are initially colored, and node j c annot color α and
β. Thus (9) follows.
The forcing graph can be used to draw conclusions
about the forcing process for G based on the derived
set:
Lemma 2. Consider V
l,1
as a ZFS for G. For all
v ∈ D(
¯
G
i j
,V
l,1
) with i ∈ V
u
and j ∈ V
c
, an FC
C (G,V
l,1
) = { c
1
,. .. ,c
|V |−|V
l,1
|
} exists with c
i
= u
′
⇀
v
′
such that:
• ∃ c
i
1
,c
i
2
∈ C (G,V
l,1
) with:
c
i
1
= u
′
⇀ v, c
i
2
= ˜v ⇀ i, i
1
< i
2
(10)
• ∄ c
i
3
∈ C (G,V
l,1
) with:
c
i
3
= j ⇀ ˜u and i
3
< i
2
. (11)
Proof. Lemma 1 states that a forcing graph
¯
G
i j
for a ZFS of G prevents the coloring of agent i.
Consequently, v ∈ V
u
∩ D(
¯
G
i j
,V
l,1
) implies the
presence of a FC C (G,V
l,1
) in G with the same
leader set V
l,1
, where all nodes v are co lored prior to
the coloring of node i, according to (10). Moreover in
¯
G
i j
, node j consistently has two uncolored neighbors
that remain uncolored (as established by Lemma 1),
ensuring that all n odes v can be colored before node
i without node j coloring any of its neighbors. This
directly validates cond ition (11).
Corollary 1. If v 6∈ D(
¯
G
i j
,V
l,1
) with V
l,1
as a ZFS
for G, then ∄ C (G, V
l,1
) such that conditions (10) and
(11) are satisfied.
It is shown next how the for cing graph can be used
in order to find an edge (i, j) to specifically add node
j to the set of FA of another node i:
Theorem 2. Consider i ∈ V
u
, j ∈ V
c
, i 6∈ N
j
and
V
l,1
as a ZF S for G. Adding the undirected ed ge (i, j)
to G, resulting in G
′
= (V , E
′
) with E
′
= {E ∪(i, j)}
leads to j ∈ F
i
(G
′
,V
l,1
) if and only if the following
condition holds for all nod es l ∈ N
j
:
l ∈ D(
¯
G
i j
,V
l,1
). (12)
Proof. Based on Lemma 2, condition (12) satisfied
∀l ∈ N
j
implies that a FC C (G,V
l,1
) exists for which
(10) and (11) holds. This implies th at all neig hbors of
j can be colored before i is colored, without requiring
j to force any of its neighbors. Thus, the force j ⇀ i
is possible in G
′
, leading to j ∈ F
i
(G
′
,V
l,1
).
To demo nstrate the necessity of condition (12), con-
sider the case in which the edge (i, j) is added to G,
while
∃ l
′
∈ N
j
: l
′
6∈ D(
¯
G
i j
,V
l,1
) (13)
applies. According to Corollary 1, ∄ C (G, V
l,1
) such
that l
′
is co lored while (10) and (11) are true, i.e.
either j ⇀ l
′
or i
1
> i
2
with c
i
1
: ˜v ⇀ l
′
, c
i
2
= u
′
⇀ i.
In the first case, edge (i, j) prevents j ⇀ l
′
because
i is an additional uncolored neighbor, making it
impossible f or j to color i or l
′
, consequently
j 6∈ F
i
(G,V
l,1
). In the second ca se, j 6∈ F
i
(G,V
l,1
)
follows directly from the fact that i is colore d before
l
′
, implying that up to the point of the coloring of
i, node j has more than one uncolored neighbors,
preventing j ⇀ i. Thus (12) has to apply ∀l ∈ N
j
such that j ∈ F
i
(G
′
,V
l,1
) after adding (i, j) to graph
G, thereby establishing the nece ssity of (12).
Fig. 3 shows an example in which condition (1 2)
holds ∀l ∈ N
4
, such that adding edge (5, 4) to the
graph resu lts in 4 ∈ F
5
(G
′
,V
l
) (as already illustrated
in Fig. 2). Note tha t the computational complexity of
verifying condition (1 2) for a specific pair of nodes
is equivalent to that of computing D(
¯
G
i j
,V
l,1
), for
which the effort is of order O(N + |E|) (see (Brimkov
et al., 2019)).
In order to show that adding the edge (i, j) by The-
orem 2 increases the cardinality of the set of FA of i,
as required in (7), the following result is derived first:
Lemma 3. For l ∈ F
i
(G,V
l,1
), let an edge (i, j) b e
added to G u nder the conditions of Theorem 2, lead-
ing to G
′
. Then l ∈ F
i
(G
′
,V
l,1
) holds.
11 22
33
44
55
66
77
88
9
9
αα
ββ
¯
G
54
D(
¯
G
54
,V
l
)
Figure 3: Left: The forcing graph corresponding to graph G
from Fig 2 with i = 5 and j = 4. Right: The derived set of
the forcing graph wi th V
l
being a ZFS for G.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
140

Proof. Sinc e l is a forcing agent of i in graph G, l
and all its neighbors except of i are colored bef ore i is
colored. This can be expressed by the forcing graph
(cf. (Schmidtke et al., 2024) Theorem 3):
l ∈ D(
¯
G
i{}
,V
l,1
) ∧ N
l
\ i ⊂ D(
¯
G
i{}
,V
l,1
). (1 4)
Theorem 2 ensures that all neigh bors of j can be col-
ored by other nodes than j, before i is color ed. There-
fore, no c oloring in the derived set of the forcing
graph depends on j, implying:
D(
¯
G
i j
,V
l,1
) = D(
¯
G
i{}
,V
l,1
). (15)
From th is equality, it directly follows that:
l ∈ D(
¯
G
i j
,V
l,1
) ∧ N
l
\ i ⊂ D(
¯
G
i j
,V
l,1
). (16)
This implies that adding the edge (i, j) does not
change the coloring of all FA l ∈ F
i
(G,V
l,1
) in G
′
,
since the coloring of each of these no des does not de-
pend on the co loring of j, as shown by (15). T hus,
each FA can still be colored before i is colored. This
eventually means th at:
l ∈ F
i
(G,V
l,1
) =⇒ l ∈ F
i
(G
′
,V
l,1
), (17)
holds if G
′
results from adding (i, j) to G under th e
condition of Theorem 2 holds.
Lemma 3 shows that all FA in G remain FA in
G
′
, if the edge is added under the conditions of Theo-
rem 2. T hus, as a conseque nce of Lemma 3 together
with Theorem 2, the following result can be stated
which directly validates (7):
Corollary 2. If the graph G is augmented by adding
the edge (i, j) and if Theorem 2 holds, then
|F
i
(G,V
l,1
)| < |F
i
(G
′
,V
l,1
)|, (18)
holds true.
While augmenting G with an edge (i, j) under the
conditions of Th eorem 2 gu arantees an increase in the
number of FA for no de i, Corollary 2 does not pro-
vide insights into the set of FA of other nodes. To
address this shortcom ing, the following proposition
demonstra te s that a ZFS of G remains valid for the
augmen te d gra ph G
′
under the same conditions:
Proposition 1. If V
l,1
is a ZFS of G a nd if an edge
(i, j) is added to G accrding to Theorem 2, V
l,1
re-
mains a ZFS for the resulting graph.
Proof. The graph G
′
follows from G, by connecting
an uncolored node i with a co lored node j, while l ∈
D(G
i j
,V
l,1
) holds ∀l ∈ N
j
with V
l,1
being a ZFS for
G. This condition directly implies:
l ∈ D(G
{} j
,V
l,1
) ∀ l ∈ N
j
, (19)
where G
{} j
is the forcing graph with α a nd β only
connected to node j. Th is means tha t all neighbo rs
of j can be colored by other nodes in G
{} j
, ensuring
that the addition of the edge (i, j) does not disrupt the
zero f orcing process initiated by V
l,1
. Therefore, V
l,1
remains a ZFS of G
′
.
Since V
l,1
remains a ZFS in G
′
, the fo llowing con-
dition holds true ∀i
′
∈ V
u
\ i:
F
i
′
(G
′
,V
l,1
) ≥ 1. (20)
Comparing the set F
i
′
(G
′
,V
l,1
) of each ag ent i
′
∈ V
u
\
i to F
i
(G
′
,V
l,1
), the following two cases can occur:
|F
i
′
(G
′
,V
l,1
)| ≥ |F
i
′
(G,V
l,1
)| ∀i
′
∈ V
u
\ i or (21)
∃i
′
∈ V
u
\ i : |F
i
′
(G
′
,V
l,1
)| < |F
i
′
(G,V
l,1
)|. (22)
In case (21), the number of FA of all uncolored node s
stays the sam e or has increased. This is the desired
case, as the resilience of the whole networked system
has increased. In the secon d case (22), the number
of FA has decreased for at least one unco lored node
in the graph. This implies that, while the resilience
has increased for at least node i, it has decreased fo r
at least one oth e r node. Thus, in this case, only a
local increase in resilience is achieved. This can be
advantageous, for instance, when a f orcing agent is
added to a node with a small FA set, even if anoth er
node with a large FA set loses one of its FAs in the
process.
Fig. 2 illustrates the case (21). I nterestingly, in
this case, the aug mentation by the edge (5,4) makes
the leader set V
l
= {1; 2; 3; 4; 8;9} a 1−LFS of graph
G
′
, meaning that the system stays SSC despite any
removal of an edge or a node.
Investigating how to ensure the desired case (21)
will be a focus of f uture work. The following section
investigates how frequently the conditions introduced
hold in random graphs, allowing for the addition of
edges while enhancing resilient strong structural co n-
trollability.
5 NUMERICAL EXAMPLE
This section investigates the effectivene ss of the pro-
posed approach through numerical experiments for
random gra phs. The study proceeds in two parts:
firstly, the proposed approach is evaluated w ith re-
spect to graph size, network density, and leader set
size, and secondly, the approach is compared to an
existing method from literature.
Enhancing Resilience of Strong Structural Controllability in Leader-Follower Networks
141
5.1 Analysis Across Network
Parameters
The following three questions are addressed through
numerical experiments:
• How frequently ca n an edge be found that en-
hances resilience , either locally or globally, de-
pending on the size and density of the network?
• Which share of edges contributes to resilience of
the whole network?
• How does the size o f the leader set affect the oc-
currenc e of edges which enh ance resilience?
To investigate these questions, Erd¨os–R´enyi graphs
G(N, p) are used, in which N represents the set of
nodes and p denotes the probability of an edge ex-
isting between two nodes (Erd¨os an d R´enyi, 1959).
A higher value of p results in a den ser network, as it
increases the expected number of edges in the graph .
The ana lysis focuses on the addition of edges to crit-
ical nodes, defined as node s w ith a forcing agent set
of cardinality one, i.e., K : {i ∈ K | F
i
(G,V
l
) = 1}.
These node s represent structural bottlenecks in the
sense that SSC depends on a single neighbor to ensure
controllability. The removal of this neighbor r esults in
a loss of SSC. To mitigate this v ulnerability, the pos-
sibility of adding FA by adding edges is examined,
which would enhance resilience without introducin g
further leader agents.
The set
ˆ
E consists of edge s satisfying Theorem 2,
with i ∈ K and j ∈ V
l
. The sub set of edges that
enhance resilience for the whole network is denoted
by E
⋆
, mea ning that the condition (21) holds wh e n
any edge in E
⋆
is added to G. Furthermore, the ratio
|E
⋆
|/|
ˆ
E| reflects the share of added edges for which
condition (21) h olds, relative to all edges that can be
added according to Theorem 2. For all of the upcom-
ing tests, 10 instances of graphs are randomly gen-
erated and the average is shown below (conside ring
only connected graphs G(N, p)). In all tests V
l,min
denotes the leader set with min imal cardinality deter-
mined by exhaustive search.
First, the dependency of the sizes of K ,
ˆ
E, and
E
⋆
on the size |V
l
| o f the leader set is examined for a
fixed number of agents N = 20 and an edge probabil-
ity of p = 0.2. To increase the size of each leader set,
an additional leader is randomly chosen from among
the unc olored nodes. The results are presented in Ta-
ble 1.
For the leader set V
l,min
, only very few edges in
ˆ
E c a n be identified, and none of them belongs to E
⋆
.
This occurs because, in the smallest possible leader
set configuration, there is typic ally not enough redun-
dancy to color the neighbors of a leader if the leade r
Table 1: Evaluation of the effect of the size of the leader set
size on the number edges which can be added (according
to Theorem 2) to critical nodes K in random graphs with
N = 20 and p = 0.2.
|K | |
ˆ
E| |E
⋆
| |E
⋆
| · |
ˆ
E|
−1
|V
l
| = |V
l,min
| 7.6 0.5 0 0
|V
l
| = |V
l,min
| + 1 5.8 5.8 2.6 0.45
|V
l
| = |V
l,min
| + 2 3.6 6.6 3.1 0.47
|V
l
| = |V
l,min
| + 3 2.1 5.2 3 0.58
itself is prevented f rom coloring, as required by The-
orem 2. As a result, edges in
ˆ
E are rarely identified
in this setting. Increasing the cardinality of the leader
set leads to a reduction in |K |, while the size of
ˆ
E in-
creases. Notably, the portion of edges in
ˆ
E that also
belongs to E
⋆
appears to grow with the size of the
leader set. Addin g just one agent to V
l,min
already re-
sults in a significant increase in both |
ˆ
E| and |E
⋆
|. For
this reason, this configuration is used in the f ollowing
simulations.
Next, the influence o f the network density on th e
applicability of Theorem 2 is investigated. To this
end, the edge probability p is var ie d, where smaller
values result in sparser networks and larger values
correspo nd to denser top ologies. The results for a
fixed number of N = 20 nodes are summarized in Ta-
ble 2.
Table 2: Investi gation of the effect of the network density
on the number of edges which can be added according to
Theorem 2, considering criti cal nodes K in random graphs
with N = 20 and |V
l
| = |V
l,min
| + 1.
p |V
l
| |K | |
ˆ
E| |E
⋆
| |E
⋆
| · |
ˆ
E|
−1
0.15 6.4 8.6 14.8 7 .5 0.51
0.2 7.1 5.8 5.8 2.6 0.45
0.25 8.6 5.8 5.5 4.1 0.75
0.3 9.5 5.1 4.3 3.3 0.77
0.35 10. 5 3.4 4.4 1.8 0.41
With increasing network density, a larger leader
set is required to ensure SSC, while the number of
critical nodes K decreases – an effect already ob-
served in Table 1. I n con trast, sparser networks allow
for a greater number of edges in
ˆ
E, as redundancy
in forcing is easier to establish. The share of edges
in E
⋆
also belonging to
ˆ
E ranges between 41% and
77%, with the maximum observed at p = 0.3 and the
minimum at p = 0 .35. Investigating the cause o f this
variation is subject of future work.
Lastly, the influence o f the number of n odes N o n
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
142

the applicability of Theorem 2 is examined. To this
end, N is va ried while keeping the edg e probability
p and |V
l
| constant. The results are summarized in
Table 3.
Table 3: Effect of the graph size on the number of edges
which can be added according to Theorem 2 for cri ti-
cal nodes K in random graphs w ith p = 0.2 and |V
l
| =
|V
l,min
| + 1.
N |V
l
| |K | |
ˆ
E| |E
⋆
| |E
⋆
| · |
ˆ
E|
−1
10 4.3 3 3.7 2.7 0.73
15 5.5 5.8 8.4 4.6 0.55
20 5.8 5.8 5.8 2.6 0.45
25 10 .4 6.2 5.8 2.7 0.47
30 13 .3 6.5 7.4 4.2 0.57
As the g raph size increases, more leader agents
are required to ensure SSC, and the number of critical
nodes K also grows. However, the size of
ˆ
E a ppears
to be largely inde pendent of N. The same holds for
the ratio |E
⋆
|/|
ˆ
E|, with the highest value observed
for N = 10, followed by N = 30, an d the lowest for
N = 20 .
In summary, increasing the cardinality of the
leader set slightly beyond V
l,min
has the most signifi-
cant impact. The n umber o f edges in
ˆ
E increases with
sparser and larger graphs. In contrast, the portion of
edges in E
⋆
relative to
ˆ
E (i.e., those improving re-
silience at the network level) appears largely indepen -
dent of the graph size and density, ranging be twe en
41% and 77%.
5.2 Comparison of Edge Augmentation
and an LFS Approach
The proposed method is now compared to the use
of a 1-LFS (cf. Section 2.3), i.e., a set of leaders
that guarantees SSC is maintained in the case a sin-
gle agent leaves the network. The evaluation is per-
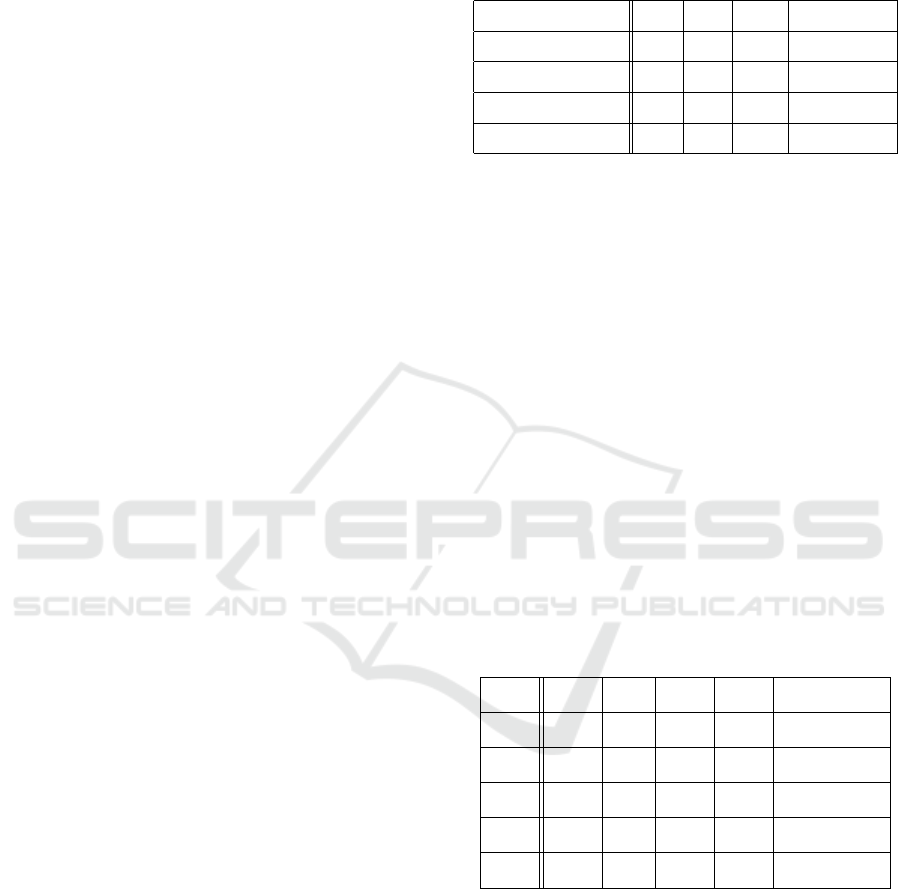
formed on the Erd¨os–R´enyi graph G with N = 30
and p = 0.12 shown in Fig. 4. A critical node is as-
sumed to be k nown: with the ze ro-for c ing set V
l
=
{1,2,3,4,6,10,20,23, 29, 30} (of size |V
l,min
| + 1),
node 11 is critical since F
11
(G,V
l
) = {12}. Thus, if
node 12 leaves the graph, node 11 cannot be colored
and th e network loses the SSC property.
To evaluate condition (1 2), the derived set on the
forcing graph
¯
G
i j
is computed for i = 12 an d j ∈ V
l
.
For j = 1 , Theo rem 2 holds, implying th at adding the
edge (1,11) to the graph expands the set of forcing
agents of node 11 to F
11
(G
′
,V
l
) = {1,12}. Conse-
quently, even if node 1 2 leaves, th e system remains
SSC since the coloring of no other agent depends
solely on node 12. The evaluation of Theorem 2 re-
quires 60 ms in MATLAB R2021b on a machine with
32 GB RAM and an Intel Core i7-14700 processor.
In contrast, the 1-LFS V
l,1-LFS
=
{1,2,4,5,7,10,11,13, 14, 20,23,30}, obtained
by using the heuristic from (Abbas, 2023), is com-
puted in 4.12 s and introduces two additional leaders
in comparison to V
l
. Since the procedure is heuristic,
minimality of the set size is not guaranteed. Usin g the
integer-programming-based method f rom ( A la meda
et al. , 2024) to compute a 1-LFS of minimal cardi-
nality does not produce a solution within one hour
of computation, which illustrates the hardness of the
problem.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Figure 4: Erd¨os–R´enyi graph G(30,0.12) used for evaluat-
ing resilience. Node 11 is a critical node when considering
the zero-forcing set V
l
= {1,2,3, 4,6,10,20,23,29,30} (in-
dicated by the black nodes). Adding the dashed edge (1,11)
expands t he set of forcing agents of node 11 by including
node 1 to enhance the resilience of the network. T he red
nodes indicate a 1−LFS for the network.
6 CONCLUSIONS
Conditions were spe cified for identifying edges that
can be added to a network in order to enhance resilient
strong structural controllability, eith er locally or f or
the entire network. The proposed method is based on
the notion of forcing graphs, which extend the origi-
nal graph by connecting dummy agents in a specific
manner. Utilizing the concept of zero-forcing, a con -
dition was estab lished that must hold fo r the neigh-
bors of a lead er agent in the forcing graph. This con-
dition ensures that adding an edge from the leader
agent to a fo llower agent in c reases the follower’s re-
silience.
Simulation studies demonstrate that such edges
can frequently be identified when the size of the
leader set exceeds the minimally required size to
Enhancing Resilience of Strong Structural Controllability in Leader-Follower Networks
143

achieve strong structur al controllability. Furthermore,
the sparser and larger the graph is, the more edges can
be found that enhance network resilience. Notably,
the portion of added edges that improve resilience
globally, rather than just locally, remains independent
of the graph’s sparsity and size.
Future research should explore how the proposed
method can be extended to directly ide ntify edges
which enhance resilient SSC for the entire network.
REFERENCES
Aazami, A. (2008). Hardness results and approximation
algorithms f or some problems on graphs. PhD thesis,
University of Waterloo.
Abbas, W. (2023). Resilient strong st r uctural controllability
in networks using leaky forcing in graphs. In IEEE
American Control Conf., pages 1339–1344.
Abbas, W., Shabbir, M., Jaleel, H., and Koutsoukos, X.
(2020a). Improving network robustness through edge
augmentation while preserving strong structural con-
trollability. In American Control Conf., pages 2544–
2549.
Abbas, W., Shabbir, M., Yazicioglu, A. Y., and Akber, A.
(2020b). Tradeoff between controllability and robust-
ness in diffusively coupled networks. IEEE Transac-
tions on Control of Network Systems, 7(4):1891–1902.
Abbas, W., Shabbir, M., Yazıcıo˘glu, Y., and Koutsoukos,
X. (2024). On zero forcing sets and network
controllability—computation and edge augmentation.
IEEE Transactions on Control of Network Systems,
11(1):402–413.
AIM Minimum Rank - Special Graphs Work Group (2008).
Zero forcing sets and the minimum rank of graphs.
Linear Algebra and its A pplications, 428(7):1628–
1648.
Alameda, J. S., Dillman, S., and Kenter, F. (2024). Leaky
forcing: A new variation of zero forcing. Australasian
Journal of Combinatorics, 88(3):306–326.
Antsaklis, P. J. and Michel, A. N. (1997). Linear systems.
McGraw-Hill.
Brimkov, B., Fast, C. C., and Hicks, I. V. (2019). Computa-
tional approaches for zero forcing and related prob-
lems. European Journal of Operational Research,
273(3):889–903.
Chapman, A. and Mesbahi, M. ( 2013). On strong structural
controllability of networked systems: A constrained
matching approach. In IEEE American Control Conf.,
pages 6126–6131.
Chen, X., Pequito, S., Pappas, G. J., and Preciado, V. M.
(2019). Minimal edge addition for network controlla-
bility. I EEE Transactions on Control of Network Sys-
tems, 6(1):312–323.
Egerstedt, M., Martini, S., C ao, M., Camlibel, K., and Bic-
chi, A. (2012). Interacting with networks: How does
structure relate to controllability in single-leader, con-
sensus networks? IEEE Control Systems Magazine,
32(4):66–73.
Erd¨os, P. and R´enyi, A. (1959). On random graphs i. Pub-
licationes Mathematicae Debrecen, 6:290.
Monshizadeh, N., Zhang, S., and Camlibel, M. K. (2014).
Zero forcing sets and controllability of dynamical sys-
tems defined on graphs. IEEE Transactions on Auto-
matic Control, 59(9):2562–2567.
Mousavi, S. S., Haeri, M., and Mesbahi, M. (2021).
Strong structural controllability of networks under
time-invariant and time-varying topological pertur-
bations. IEE E Transactions on Automatic Control,
66(3):1375–1382.
Pasqualetti, F., Zhao, S., Favaretto, c., and Zampieri, S.
(2020). Fragility limits performance in complex net-
works. Sci Rep, 10(1):1–9.
Patel, P. I., Suresh, J., and Abbas, W. (2024). Distributed de-
sign of strong structurally controllable and maximally
robust networks. IEEE Transactions on Network Sci-
ence and Engineering, 11(5):4428–4442.
Porfiri, M. and di Bernardo, M. (2008). Criteria for global
pinning-controllability of complex networks. Auto-
matica, 44(12):3100–3106.
Schmidtke, V., Al-Maqdad, R. K., and Stursberg, O. (2024).
Maintaining strong structural controllability for multi-
agent systems with varying number of agents. In IEEE
Conf. on Decision and Control, pages 3178–3184.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
144
