Research on Stock Price Prediction Based on the ARIMA Model

Ziyi Yang

School of Mathematics and Statistics, Huangshan University, Huangshan, Anhui, 245021, China

Keywords: Stock Price, ARIMA Model, Forecasting.

Abstract: In the financial field, stock prices have always been of great concern. Accurately and effectively predicting

stock prices is beneficial for investors to make reasonable decisions and avoid risks. The autoregressive

integrated moving average (ARIMA) model can effectively capture the fluctuation trend of historical stock

prices. This paper constructs an ARIMA model to predict the closing price of Zomato on that day. The results

show that compared with the real value, the root mean square error (RMSE) value predicted by the ARIMA

model is relatively small, only 4.6172, reflecting that the ARIMA model has high accuracy in short-term

forecasting (STF). In the long-term forecast, other non-linear factors should be considered, and other models

should be combined to make improvements and optimizations to improve the accuracy of the forecast. This

research will benefit both providing an effective reference for investors in short-term stock price forecasting

and further improvement and perfection of stock price forecasting in the future.

1 INTRODUCTION

As the most common and wide-ranging investment

method, stocks have long attracted the attention of

investors. The high return of stocks is accompanied

by higher risks, and accurate prediction of stock

prices facilitates obtaining considerable returns, so

this issue has been a hot topic in investment analysis

(Li, 2014). However, in the complex stock market,

stock prices are affected by many factors, which

makes it an arduous task to accurately predict stock

prices (Xu & Liang, 2019). ARIMA is a widely used

and effective model for time series forecasting,

particularly in stock price prediction.

At present, researchers have made progress in the

field of stock price forecasting using the ARIMA

model, which has a certain reference value. Wu &

Wen (2016) established an ARIMA (3,1,1) model to

dynamically and statically predict the closing price

(CP) of Huatai Securities. The relative error between

the predicted value fitted by the model and the real

value is only 0.0135, which verifies that the ARIMA

model has high accuracy in stock price forecasting.

Yang & Zhang (2021) concluded that the ARIMA

model can provide some decision-making suggestions

for policymakers in stocks’ STF through the example

analysis of Dazhong Public Utilities Stock. The

https://orcid.org/0009-0009-2785-515X

values obtained by Zhang et al. (2025) reflected that

the ARIMA model has high accuracy. The overall

fitting moderation, Ljung-Box Q test, and

normalization of Bayes’ information criterion (BIC)

results based on Bayes' decision rule all reflected the

better data fitting effect of the ARIMA model and the

higher short-term prediction accuracy.

The ARIMA model shows great potential in stock

price forecasting. This paper takes Zomato's CPs over

the past three years as the dataset, the ARIMA model

is introduced for prediction, and its advantages and

limitations are analyzed. Finally, this paper will

explore the improvement direction of the ARIMA to

provide a reference for follow-up research.

2 DATA SELECTION AND

RESEARCH METHODS

2.1 Dataset

The data used in this study comes from Kaggle

(Kaggle, 2024). The stock prices of Zomato from July

23, 2021, to February 7, 2024, a total of 632 data

points, were selected to build a model for short-term

stock price prediction.

374

Yang, Z.

Research on Stock Price Prediction Based on the ARIMA Model.

DOI: 10.5220/0013826100004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 374-378

ISBN: 978-989-758-774-0

This paper selects the date and the stock’s CP on

that day as indicators for analysis. First, stock price

data is recorded in chronological order, changing over

time and affecting each other. Dates are the basis of

time series data analysis, which can help identify the

trend of stock prices over time and whether stock

prices have seasonal changes. Secondly, the CP is the

last transaction price before the end of each trading

day, which is an important indicator of concern. The

CP can be used to identify the long-term trend of stock

prices and is an important factor in predicting stock

prices.

2.2 Method Introduction

In this paper, the ARIMA (p, d, q) model is selected

to process the time series data of stock prices.

Autoregressive (AR) is used to deal with the linear

relationship between current data and past data. The

difference (D) processes the non-stationary time

series, which is brought to a stationary state by

differential processing of up to order 2. The moving

average (MA) is used to represent the linear

relationship between the current value and the past

error term. The partial autocorrelogram determines

the appropriate p, q order. The appropriate difference

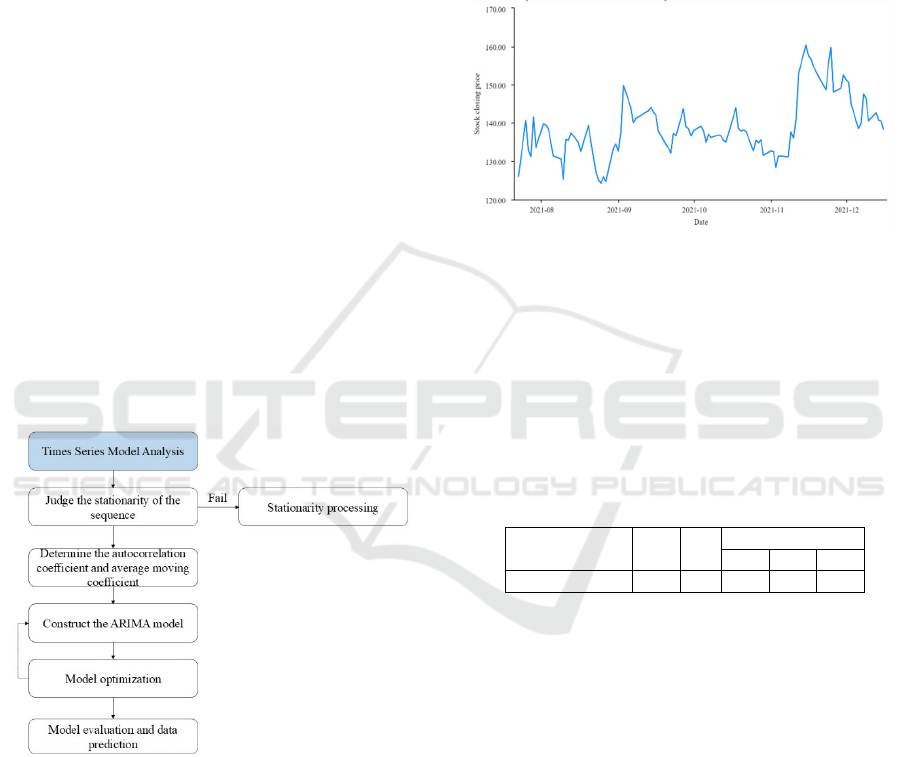
order is obtained by the ADF test. As shown in Figure

1, the overall flow is presented.

Figure 1: The structure of the ARIMA (Picture credit:

Original).

3 RESULTS AND DISCUSSION

3.1 Data Stationarity Test

The time series used to build the ARIMA model must

be a stationary series. As shown in Figure 2, the

horizontal axis coordinate is the date, the vertical axis

coordinate is the corresponding CP of the stock on

that day, and the unit is yuan.

Figure 2: Timing diagram of stock CP (Picture credit:

Original)

As can be seen from Figure 2, this group of data is

a stationary series, which fluctuates continuously

around the mean value in general, and have no

obvious continuous upward or downward trend. In

order to verify that the original data is stable,

performing the ADF unit root test on this group of

data is necessary to obtain more accurate judgment

results.

Table 1: Stock CP-ADF inspection

Differential ordert

Critical value

1% 5% 10%

0 -3.4020.011-3.498 -2.891 -2.583

As shown in Table 1, for the CP of stocks, the p-

value of 0.011<0.05 in the ADF test of this time series

is significant, and the t-statistic is -3.402, which is less

than the critical value of 5% and 10%. Therefore, the

certainty of rejecting the null hypothesis is 95%,

namely the original series does not have a unit root,

so the original series is a stationary series.

3.2 Model Order Determination and

Evaluation

According to the stationarity, the difference order

I(d)=0, determining the autocorrelation coefficient

and moving average coefficient of the AR and MA

parts, namely the p and q orders, is necessary to build

ARIMA model now.

Research on Stock Price Prediction Based on the ARIMA Model

375

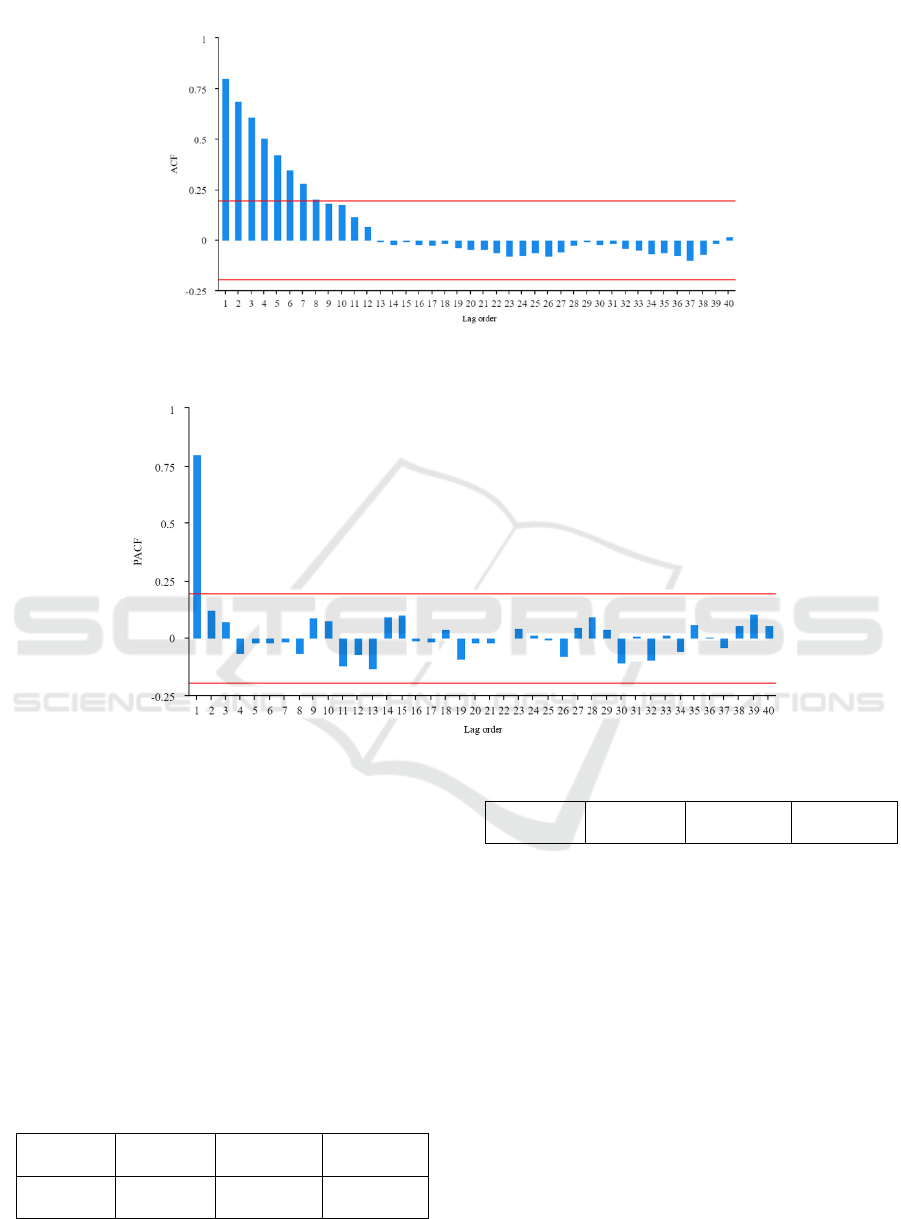
Figure 3: Original sequence autocorrelatin graph (Picture credit: Original)

Figure 4: Original sequence partial autocorrelation graph (Picture credit: Original)

Figures 3 and 4 show the autocorrelation and

partial autocorrelation of the original time series. The

autocorrelation function suggests a first-order tail,

and the partial autocorrelation function truncates at

the first order, indicating an ARIMA (1,0,1) model.

However, Akaike information criterion (AIC) and

BIC are used to determine the optimal p and q values.

Based on these, four models are tested:

ARIMA(1,0,0), ARIMA(1,0,1), ARIMA(2,0,0), and

ARIMA(2,0,1). The AIC and BIC values

corresponding to the above models are calculated

with SPSSAU, and the results are shown in Table 2.

Table 2: ARIMA fitting model AIC and BIC values

ARIMA(1

,0,0

)

ARIMA(1

,0,1

)

ARIMA(2,

0,0

)

ARIMA(2,

0,1

)

AIC592.0

593.254 593.442 595.098

BIC599.8

603.675 603.862 608.124

Table 2 clearly shows the comparison of AIC and

BIC values of the four ARIMA models. According to

the information criterion, the model with the smallest

AIC and BIC values is the better model, which can

better fit the time series. As can be seen from Table 2,

the AIC and BIC values corresponding to the

ARIMA(1,0,0) model are the smallest, so the

ARIMA(1,0,0) model, namely the AR(1) model, is

finally selected to predict and analyze the CP of the

stock. The formula for this model is

y(t)=27.645+0.800*y(t-1).

3.3 Residual Test

3.3.1 White Noise Test

After parameter estimation, the model's residuals are

tested for white noise. If the residuals show no

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

376

autocorrelation, the model is considered well fitted.

Otherwise, the model will be optimized. The test

results are shown in Table 3. A p-value greater than

0.1 for Q1-Q20 indicates that the residuals pass the

test.

Table 3: Statistics Table

item Statistics P value

0.235 0.628

0.279 0.870

1.170 0.760

1.171 0.883

1.171 0.948

1.177 0.978

1.231 0.990

2.812 0.946

2.955 0.966

5.180 0.879

5.181 0.922

5.343 0.946

7.642 0.866

8.352 0.870

8.559 0.899

8.583 0.930

8.712 0.949

9.151 0.956

9.336 0.967

9.358 0.978

Table 3 shows the statistical information of model

Q, including statistical value and p-value. It can be

seen from Table 3 that all p-values are greater than

0.1, namely the residuals are white noise, namely

residuals have no autocorrelation, indicating that the

established ARIMA model is reasonable and

effective.

3.3.2 LM Test

As shown in Table 4, the LM test results of the model

residual sequence can be observed.

Table 4: Residual term LM test

F statistics 0.849

value 0.584

T *R

Statistics 8.732

value 0.558

It can be seen from Table 4 that in the residual

term LM test, the corresponding P values of F statistic

and T * R ^ 2 statistic are both greater than 0.05,

which further verifies that residual sequence have no

sequence correlation so it can be determined that the

ARIMA model established has good fitting effect and

high accuracy.

3.4 Model Prediction

Since the established ARIMA (1,0,0) model has

passed the residual test, it can make a short-term

forecast of Zomato stock price and predict the stock

CP in the next 12 trading days.

Table 5: AR (1) model prediction results

Date Predicted value Actual value

2024-02-08 138.409 144.10

2024-02-09 138.416 149.54

2024-02-12 138.422 153.80

2024-02-13 138.427 154.75

2024-02-14 138.430 152.25

2024-02-15 138.433 154.85

2024-02-16 138.436 156.70

2024-02-19 138.438 157.50

2024-02-20 138.439 161.05

2024-02-21 138.404 158.65

2024-02-22 138.441 162.10

2024-02-23 138.442 164.05

As shown in Table 5, the comparison between the

model-predicted value and the real value of the stock

CP in the next 12 periods can be observed.

Table 6: Model error assessment

RMSE MSE MAE MAPE

4.6172 21.3189 3.4144 0.0245

Table 6 shows that the RMSE of the AR(1) model

is 4.6172, the MSE is 21.3189, the MAE is 3.4144,

and the MAPE is 0.0245. These indicators fully

reflect the high degree of fitting between the stock

CPs predicted by the AR (1) model and their actual

value, and the prediction results are more accurate.

Although the traditional time series prediction

model (ARIMA model) performs well in prediction,

it still has some limitations. For example, stock price

fluctuations are usually nonlinear and have complex

noise, but the ARIMA model is used to study linear

data, and it cannot find the relevant information about

nonlinear data. Therefore, accurate prediction results

cannot be obtained by only using the ARIMA model

(Zhang, 2019). ARIMA models may also have large

errors when dealing with long-term forecasts.

To obtain more accurate prediction results, a large

number of researchers have proposed improved

methods that combine the ARIMA model with other

models to reduce errors. For example, the long short-

term recurrent neural network (LSTM) is superior to

the traditional ARIMA model in predicting stock

prices, because it can capture time patterns.

Therefore, LSTM can be introduced to perform

memory storage of past information (Jiang,2025).

Gao (2021) combined the ARIMA model with the

Research on Stock Price Prediction Based on the ARIMA Model

377

deep learning model, and the results showed that the

Seq2Seq model based on the LSTM model has the

smallest mean square error in the prediction, which is

an excellent prediction tool for stock prices, and the

increase in the complexity of the neural network will

produce better prediction results. In addition, the

ARIMA model has limitations in dealing with

cyclical changes, while Prophet is more flexible and

good at processing time series data with seasonal,

trend, and holiday effects. Therefore, Anusha et al.

(2021) introduced Facebook Prophet based on the

ARIMA model, which successfully solved the

problem of dealing with the elements related to

seasonality in the data.

4 CONCLUSION

Stock price prediction has always been a highly

concerned and challenging problem, which can be

effectively predicted by using time series models.

This paper constructs an ARIMA model to fit and

predict Zomato stock price, and finds that the model

is effective in capturing time series and volatility. At

the same time, this paper found that the error between

the predicted values of the stock prices of the previous

periods and the real values is small and within the

allowable error range by comparing the predicted

stock prices of the 12 periods. As time goes on, the

error between the predicted value and the real value

of the stock price gradually increases, which fully

demonstrates that the ARIMA model shows high

accuracy in short-term prediction. However, due to

the complexity and nonlinear characteristics of the

stock market, the ARIMA model has some limitations

when dealing with long-term forecasting. Future

research can try to combine the ARIMA model with

machine learning models, such as decision tree,

LSTM, etc., to improve the model's prediction

performance. This paper provides strong theoretical

support for stock price forecasting and has practical

application value. Furthermore, the improvement

methods and suggestions for future research on stock

price forecasting are also presented in this paper.

REFERENCES

Aradhak, K., 2024. Zomato stock price prediction. Kaggle.

https://www.kaggle.com/datasets/aradhakkandhari/zo

mato-stock-price-prediction/dataSSS

Gao, Z., 2021. Stock price prediction with ARIMA and deep

learning models. In 2021 IEEE 6th International

Conference on Big Data Analytics (ICBDA), pp. 61–68.

IEEE.

Garlapati, A., Krishna, D. R., Garlapati, K., Rahul, U., &

Narayanan, G., 2021. Stock price prediction using

Facebook Prophet and ARIMA models. In 2021 6th

International Conference for Convergence in

Technology (I2CT), pp. 1–7. IEEE.

Jiang, S., 2025. Stock price prediction based on LSTM

model. Jiangsu Business Theory, (01), 83–86.

Li, Y., 2014. Stock price prediction based on the ARIMA

model and neural network model – taking the Bailian

Group as an example. Modern Marketing (Xueyuan

Edition), (04), 96–97.

Weng, Z., 2023. Stock price analysis and forecast based on

ARIMA model – taking Construction Bank as an

example. Modern Information Technology, 7(14), 137–

141.

Wu, Y., & Wen, X., 2016. Short-term stock price forecasting

based on the ARIMA model. Statistics and Decision,

(23), 83–86.

Xu, S., & Liang, X., 2019. Research on stock price

prediction based on the ARIMA-GARCH model.

Journal of Henan University of Education (Natural

Science Edition), 28(04), 20–24.

Yang, Y., & Zhang, M., 2021. Empirical analysis of stock

prices based on ARIMA model. Science and Technology

Information, 19(29), 121–123+127.

Zhang, Q., 2019. Analysis of the price forecast of GEM

stocks based on the ARIMA-SVM combination model.

Guangxi Quality Supervision Report, (12), 131–132.

Zhang, Y., Xiao, H., Zhang, Y., & Zhao, J., 2025. Stock

price forecast based on ARIMA model. Statistics and

Application, 14(4), 10–18.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

378