Research on the Influencing Factors of GPA Based on Multiple

Linear Regression

Xintong Du

School of Statistics, School of Southwestern University of Finance and Economics, Chengdu, Sichuan, China

Keywords: GPA, Influencing Factors, Multiple Linear Regression, Correlation Analysis, Descriptive Statistics.

Abstract: Academic performance is a critical determinant of future opportunities, yet the key drivers of GPA

variations remain underexplored. This study investigates the factors influencing Grade Point Average

(GPA) among university students using statistical methods, including multiple linear regression and

correlation analysis. This research aims to identify the most influential factors affecting GPA to provide

actionable insights for improving student outcomes. Data for this study were obtained from publicly

available datasets on Kaggle, which include variables such as study habits, socioeconomic background,

and academic performance. The results indicate that study hours have the most significant positive

impact on GPA, while sleep hours exhibit a significant negative correlation. Social hours, physical

activity hours and stress levels also show moderate positive effects, whereas extracurricular hours do

not significantly affect GPA. The study's limitations include the exclusion of qualitative factors. Future

research should incorporate other factors multicollinearity among predictors. Additionally, simplifying

the model and using cross-validation could enhance stability and predictive performance.

1 INTRODUCTION

Grade Point Average (GPA) is an important indicator

of academic performance and is widely used in higher

education. It not only reflects students' academic

achievements but also plays a key role in scholarship

assessments, graduate school applications, and job

competition. Therefore, researching the factors

influencing GPA is of great significance for the

formulation of educational policies, the improvement

of teaching quality, and the personal development of

students.

In recent years, with the accumulation of

educational data and the advancement of analytical

techniques, more and more studies have begun to

focus on the factors influencing GPA. The advantages

of multiple linear regression and correlation analysis

lie in their ability to quantify the impact of multiple

variables on GPA, identify key factors, and reveal the

relationships between variables. Compared to single

methods, these techniques are more suitable for

handling complex relationships involving multiple

factors. Several relevant studies have explored this

https://orcid.org/0009-0008-4660-6143

Corresponding author

topic. For instance, Yuan et al. (2024) uesd mutiple

linear regression to conclued that personality traits

like conscientiousnes s (r = 0.19 (p < 0.001)) are

strongly linked to higher GPA, while extraversion (r

= 0.05 (p < 0.05)) and openness (r = 0.06 (p <

0.05))are linked to lower GPA.Additionally,

Pascarella and Terenzini (2005) studied how study

time affects GPA. They showed that academic

engagement is important for GPA. Sirin (2005) found

that family income affects GPA through educational

resources, showing the role of socioeconomic

background in academic success. Steindórsdóttir et al.

(2024) showed that GPA has a long-term effect on

career success, linking GPA to career growth. Keles

et al. (2025) looked at how anxiety, loneliness, and

gender affect GPA, finding that these factors impact

academic performance. Li et al. (2022) showed that

learning attitudes, professional interest, and

motivation affect GPA, meaning internal factors are

as important as external ones. These studies provide

important empirical evidence for understanding the

mechanisms influencing GPA. This paper will use

multiple linear regression as the main method,

Du, X.

Research on the Inﬂuencing Factors of GPA Based on Multiple Linear Regression.

DOI: 10.5220/0013826000004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 369-373

ISBN: 978-989-758-774-0

369

combined with correlation analysis and descriptive

statistics, to explore the factors influencing GPA. This

research offers senior students a channel, through

which they can adapt their time allocation to improve

their GPA.

2 METHODOLOGY

2.1 Data Source and Description

The data used in this study is sourced from the Kaggle

open data platform, involving a dataset titled Daily

Lifestyle and Academic Performance of Students"

contains data from 2,000 students collected via a

Google Form survey (researched by Sumit Kumar,

ranging from 2023.8.1 to 2024.10.24) (Kaggle, 2024).

It includes information on study hours, extracurricular

activities, sleep, socializing, physical activity, stress

levels, and CGPA. The data covers an academic year

from August 2023 to May 2024 and reflects student

lifestyles primarily from India.

2.2 Indicator Selection and Description

In this study, the selection of indicators is divided into

quantitative and qualitative variables. The

quantitative independent variables include: study

hours per day, extracurricular hours per day, sleep

hours per day, social hours per day, and physical

activity hours per day. All these quantitative variables

undergo normalization to scale the data within a

specific range, ensuring comparability. Moreover, the

qualitative independent variable is Stress Level

(students' stress level), which is processed through

label encoding. The categories are encoded as: Low =

1, Moderate = 2, and High = 3. Meanwhile, the

dependent variable is GPA, which represents students'

academic performance and is used directly without

any processing. There is an index called

“Student_ID” among them, which is not related to this

research, so this paper deletes it.

2.3 Methodology Introduction

This research utilizes multiple linear regression

(MLR) as the primary statistical method to analyze

the factors affecting students' academic performance

(GPA). Multiple linear regression is a widely used

analytical technique that models the relationship

between a single dependent variable and multiple

independent variables. The general mathematical

representation of the regression model is formulated

as follows:

𝑦=𝛽



+𝛽



𝑥



+𝛽



𝑥



+⋯+𝛽



𝑥



+∈ (1)

where y represents the dependent variable, which

in this study corresponds to students' GPA,

𝑥



, 𝑥



...... 𝑥



denote the independent variables,

including study hours, extracurricular activities, sleep

duration, social interactions, physical activity, and

stress level.𝛽



is the intercept term, representing the

expected value of GPA when all independent

variables are zero.𝛽

,

𝛽



,...... ,𝛽



are the regression

coefficients, which quantify the impact of each

independent variable on GPA. These coefficients

indicate the magnitude and direction of influence that

each predictor variable has on academic performance.

ϵ is the error term, which accounts for variations in

GPA that cannot be explained by the included

independent variables. It is assumed to follow a

normal distribution.

To estimate the regression coefficients, this study

employs the least squares estimation method, which

minimizes the sum of squared differences between the

observed values and the predicted values of GPA. The

goodness-of-fit of the model is evaluated using the R-

squared (R2) statistic, which measures the proportion

of variance in GPA that is explained by the

independent variables included in the model. A higher

R2 value suggests a stronger explanatory power of the

model.

Before constructing the regression model, this

study conducts a correlation analysis to assess the

strength and direction of the relationships between

GPA and each independent variable. Pearson’s

correlation coefficient (r) is computed for this

purpose. The coefficient r ranges from -1 to 1 and is

interpreted as follows: Firstly, when r>0, it means a

positive correlation – as the independent variable

increases, GPA tends to increase. Similarly, when

r<0, it illustrates a negative correlation. when r≈0,

there is no significant correlation and there is no

meaningful linear relationship between the variables.

Moreover, descriptive statistics serve as the

foundation for GPA analysis by summarizing the

dataset, identifying patterns, and ensuring data quality

before performing deeper statistical modeling. By

using these methods, researchers can better interpret

how lifestyle factors influence academic performance

and set the stage for more complex analytical

techniques like correlation analysis and multiple

linear regression.

To enhance the accuracy and interpretability of

the regression model, data preprocessing is

implemented before the analysis. This step includes

handling missing data, identifying and addressing

outliers, and applying normalization techniques to

continuous variables where necessary.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

370

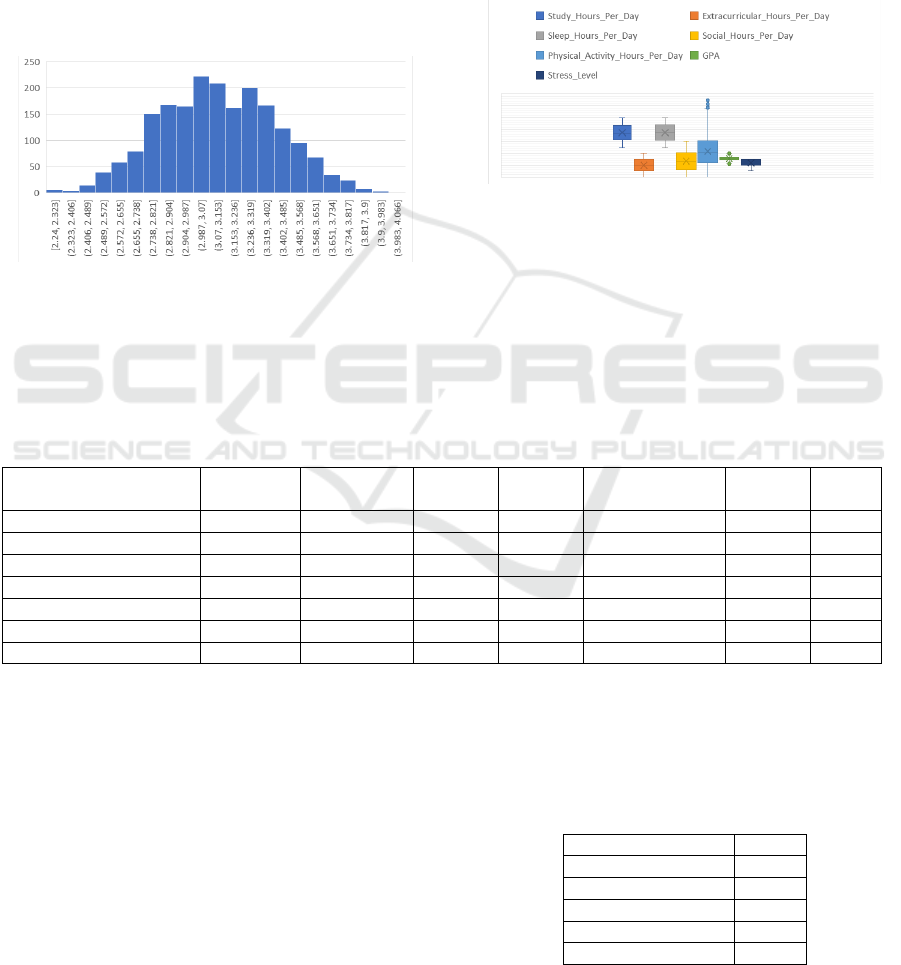
3 RESULTS AND DISCUSSION

3.1 Descriptive Statistics

The dataset used in this study includes records of

2,000 students' lifestyle habits and GPA. Figures 1

and 2 present the descriptive statistics for the key

variables.

In Figure 1, the horizontal coordinates are the

score of GPA, while the vertical coordinates represent

the number of students who got them. Figure 2

presents the central trend, dispersion, and outlier

among these factors.

Figure 1: Column diagram of GPA (photo is original)

Combined with the data and chart, here are the

conclusions:

Firstly, the average GPA is around 3.1, follows a

normal distribution, and is relatively concentrated with

a slight right skew. The median stress level is 3,

indicating that most students experience high stress.

Secondly, the standard deviation of sleep time is

0.03184, and the median is 7.4, showing a relatively

balanced distribution and the standard deviation of

study time is 0.0327, and the median is 7.5, indicating

a relatively balanced distribution. Figure 1 shows that

the distribution of GPA conforms to a normal

distribution. Figure 2 reveals some outliers in physical

exercise time, which need further investigation to

determine their impact on regression analysis.

Figure 2: Box Plot of variable influencing factors of GPA

(photo is original)

3.2 Correlation Analysis

By using Excel's data analysis tools, the calculated

correlation matrix is as Table 1:

Table 1: The box plot of GPA and influencing factors

Study

Hou

Extracurricu

lar Hours

Sleep

Hours

Social

Hours

Physical

Activit

Hours

GPA

Stress

Level

Study_Hours 1

Extracurricular Hours -0.0026 1

Sleep Hours 0.0267 0.0088 1

Social Hours -0.1378 -0.1391 -0.1936 1

Physical Activity Hours -0.4881 -0.3700 -0.4703 -0.4171 1

GPA 0.7344 -0.0322 -0.0043 -0.0857 -0.3412 1

Stress Level 0.7388 -0.0061 -0.2989 -0.0547 -0.2052 0.5504 1

Combined with the data in Table 2, here are the

conclusions: Study hours have a strong positive

correlation with GPA (r = 0.73). This means that

students who study more tend to get higher grades.

Physical activity hours have a negative correlation

with GPA (r = -0.34). This means that more time spent

on physical activity may lower academic

performance. Social hours have a weak negative

correlation with GPA (r = -0.08). This shows that

social time has little effect on academic performance.

Extracurricular involvement has a very low

correlation with GPA (r = -0.03). Sleep duration has

almost no correlation with GPA (r = -0.004). Stress

levels have a moderate to strong positive correlation

with GPA (r = 0.55). This means that students with

more stress tend to perform better academically.

Table 2: Regression Statistics Result of Multiple Linear

Regression

Regression Statistics

Multiple R 0.7355

R Square 0.5409

usted R S

uare 0.5395

Standard Erro

0.2025

Observed Value 2000

Research on the Inﬂuencing Factors of GPA Based on Multiple Linear Regression

371

Table 3: Result of Multiple Linear Regression

Coefficients Standard Erro

t Stat P-value Lower 95% U

er 95%

Interce

t 1.8273 0.0929 19.6671 0.0758*10-77 1.6450 2.009

X Variable 1 0.1618 0.0065 25.0853 0.0063*10-118 0.1745 -

X Variable 2 0 0 65535 - 0 0

X Variable 3 0.0030 0.0053 0.5635 - -0.0074 0.0134

X Variable 4 0.0088 0.0045 1.9534 0.0509 -3.5E-05 0.0177

X Variable 5 0.0075 0.0040 1.8925 0.0586 -0.0003 0.0153

X Variable 6 0.0002 0.0105 0.0197 0.9843 -0.0204 0.0208

Because there is the insignificant connection

between GPA and X Variable 2(Extracurricular

hours) in Table 3, the paper deletes this factor and

makes another form without it:

Table 4: Regression Statistics Result of Multiple Linear Regression (without X Variable 2)

Multiple R 0.8048

R Square 0.6477

usted R S

uare 0.6468

Standard Erro

0.4324

Observed Value 2000

Table 5: Result of Multiple Linear Regression (without X Variable 2)

Coefficients Standard Erro

t Stat P-value Lower 95% Upper 95%

Intercept 0.6894 0.2161 3.1903 0.0014 0.2656 1.1132

X Variable 1 0.3828 0.0133 28.8761 0.0018-150 0.3568 0.4088

X Variable 3 -0.1581 0.0107 -14.7491 0.0832-45 -0.1791 -0.1371

X Variable 4 -0.0042 0.0096 -0.4399 0.6601 -0.0231 0.0147

X Variable 5 0.0021 0.0085 0.2475 0.8045 -0.0145 0.0187

X Variable 6 0.0009 0.0478 0.0197 0.9843 -0.0928 0.0947

Above all, the paper can conclude that: The p-

value of study hours (X Variable1) is extremely small

and well below 0.05, which means it has a highly

significant positive effect on GPA (Tables 4, 5). In

contrast, the p-value of sleep hours (X Variable3) is

small enough, hurting GPA. Furthermore, social

hours (X Variable 4), physical hours (X Variable 5),

and stress level (X Variable 6) do not have significant

effects on the dependent variable, as indicated by their

high p-values. These variables are not contributing

meaningfully to the model and could potentially be

excluded in further analysis. The R2 is o.6477, which

means there is a nice variance in GPA.

3.3 Discussion

This study only considers quantifiable lifestyle

factors (e.g., study time, sleep, social activities).

However, qualitative factors such as learning

strategies, motivation, and family support may also

significantly influence GPA, but were not included.

There are a lot of surveys highlighted the significant

impact of qualitative factors on GPA. For instance,

Marley and Wilcox (2022) found that family and peer

academic social supports are predictive of academic

motivation and first-semester GPA among first-year

college students. Similarly, Pérez-Navío et al. (2023)

demonstrated that learning strategies, intrinsic

motivation, and study habits are strongly associated

with academic performance in university students.

These findings suggest that factors beyond

quantifiable lifestyle elements, such as study time and

sleep, play crucial roles in influencing GPA.

Moreover, Brambila-Tapia et al. (2022) found that

positive relationships with others, emotion

perception, and weekly physical activity hours are

associated with higher GPA in female students.

Similarly, Wu et al. (2022) demonstrated that intrinsic

motivation, need for cognition, grit, and growth

mindset are predictive of academic achievement in

high school students.

Although the R² value of 0.64 indicates that the

model explains a decent amount of variance in GPA,

future experiments may also benefit from further

simplifying the model or exploring different

combinations of predictors to avoid unnecessary

complexity. Additionally, techniques like cross-

validation could be considered to assess the stability

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

372

and generalizability of the model, ensuring

improvements in predictive performance.

However, the study also finds multicollinearity

between several variables, meaning some of the

predictors are too similar. This means the author

needs to carefully choose which variables to include

in the future to make the model more reliable.

4 CONCLUSION

This paper uses multiple linear regression as a

majority, combined with descriptive and correlation

analysis, showing a detailed correlation between GPA

and lifestyle. It shows that study habits affect GPA a

lot, with study hours being the most important factor.

More study time leads to better grades. The study

shows that sleep duration hurts GPA. In contrast,

factors like social hours, physical activity, and

extracurricular involvement have little effect on GPA.

However, the limit of the dataset and the

multicollinearity between several variables need to be

improved in future studies.

Future research should look at non-linear

relationships between variables and include other

factors, such as learning methods, motivation, and

mental health, which might help explain academic

performance better.

REFERENCES

Brambila-Tapia, C., Gálvez, M., & Martínez-Sánchez, M.,

2022. The relationship between emotion perception,

social relationships, and GPA in female students: The

role of physical activity. In Psychology, Health &

Medicine, 27(7), 1551-1563.

Keles, B., Demir, A., & Uzun, M., 2025. Anxiety,

loneliness, and gender as determinants of GPA in

university students. In Journal of Student Affairs

Research, 41(2), 123-135.

Li, Y., Zhao, L., & Wang, Q., 2022. Factors influencing

GPA in university students: The roles of learning

attitude, motivation, and professional interest. In

Journal of Educational Psychology, 58(6), 1129-1144.

Marley, L., & Wilcox, D., 2022. Family and peer academic

social supports as predictors of academic motivation

and first-semester GPA among first-year college

students. In Journal of College Student Development,

63(5), 567-579.

Pascarella, E. T., & Terenzini, P. T., 2005. How College

Affects Students: A Third Decade of Research. In

Jossey-Bass.

Pérez-Navío, E., García-Sánchez, J. N., & Figueroa, F.,

2023. The impact of learning strategies, intrinsic

motivation, and study habits on academic performance

in university students. In Sustainability, 15(4), 3497.

Sirin, S. R., 2005. Socioeconomic status and academic

achievement: A meta-analytic review of research. In

Review of Educational Research, 75(3), 417-453.

Steindórsdóttir, J., Ásgeirsson, T., & Jónsson, H., 2024. The

long-term effects of GPA on career success: Evidence

from a longitudinal study. In Journal of Higher

Education Research, 63(5), 903-918.

Wu, Z., Li, S., & Xie, Y., 2022. The influence of intrinsic

motivation, need for cognition, and grit on academic

achievement in high school students. In arXiv.

Yuan, S., Zhang, Y., & Liu, X., 2024. The influence of

personality traits on academic performance: A cross-

lagged study. In Educational Psychology, 44(4), 366-

381.

Sumit Kumar., 2025. The dataset of 2000 students’ lifestyle.

In Kaggle.

https://www.kaggle.com/datasets/steve1215rogg/stude

nt-lifestyle-dataset

Research on the Inﬂuencing Factors of GPA Based on Multiple Linear Regression

373