Comparison of Prediction Models for Heart Failure Related Data

Haoyang Zhang

Data Science, Capital University of Economics and Business, Beijing, 102627, China

Keywords: Logistic Regression, Random Forest, K-Nearest Neighbour, Heart Failure.

Abstract: Using the Heart Failure Clinic Records Dataset from Kaggle, this study assesses how well three machine

learning models-Logistic Regression, Random Forest, and K-Nearest Neighbours-predict mortality events

associated to heart failure. The dataset includes 299 patients with 12 clinical features such as ejection fraction,

serum creatinine, platelet counts, and smoking history. To guarantee reliable model training, data pretreatment

addressed outliers, missing values, and scalability concerns. For feature selection, Principal Component

Analysis (PCA) was employed to reduce dimensionality while preserving crucial data. The model's

performance was assessed using metrics of accuracy, precision, recall, and F1 score; cross-validation was

employed to ensure generalizability. According to the results, the Random Forest model outperforms K-

Nearest Neighbours (0.786) and Logistic Regression (0.812) by achieving the best accuracy of 0.907. The

Random Forest also shows superior precision (0.92) and recall (0.89), effectively balancing false positives

and negatives. The promise of machine learning in predictive healthcare is demonstrated by this work,

especially in identifying high-risk individuals for early intervention. The results highlight how well ensemble

techniques like Random Forest handle complicated clinical data and offer guidance for incorporating machine

learning into future studies and clinical practices.

1 INTRODUCTION

Many different types of people can be afflicted with

heart failure. With a frequency of 1 to 3 percent in the

average adult, it is a global pandemic that affects 64

million people globally and is more likely to occur in

developed nations (Savarese et al., 2023; Norhammar

et al., 2023). And it is a very challenging disease to

manage and treat effectively. Within 30 days

following release, over 25% of patients with heart

failure are readmitted (Khan, 2021; Javeed et al.,

2022). Therefore, the best way to reduce mortality

from heart failure is prevention. Numerous systematic

studies show that patients with heart failure are

readjusted not only due to deteriorating symptoms but

also because of psychological variables such

depression, multimorbidity, older age, and non-

adherence to treatment (Retrum et al., 2013). To

avoid risk factors comprehensively, predictive

modeling research is necessary.

A medical disease known as heart failure occurs

when the heart cannot adequately pump blood to

fulfill the body's metabolic demands. There are four

kinds of this complicated clinical syndrome: systolic

https://orcid.org/0009-0002-8883-1353

dysfunction, diastolic dysfunction, right heart failure,

and left heart failure. When the left heart fails, the

arterial system does not get enough blood, which

causes pulmonary hypertension and breathing

difficulties. Nausea and vomiting are symptoms of

right heart failure, which is caused by the heart's right

ventricle's inability to adequately pump blood to the

lungs for oxygenation. Systolic and diastolic

dysfunction have the characteristics of losing part of

the functional muscle of the ventricle, unable to

effectively contract and ejection, and increasing

diastolic filling pressure, which will work together to

produce dyspnea, palpitation and fatigue (Rockwell,

1999).

Heart failure ranks sixth globally and is one of the

top causes of mortality, according to the World

Health Organization's (WHO) Global Health

Estimates report. About 1.5 million people die each

year from heart failure, accounting for 2.5 percent of

all deaths worldwide (Forouzanfar et al., 2017). Heart

failure has been researched for many years and is

linked to low survival, frequent hospitalizations, and

a poor quality of life (Ho et al., 1993). Therefore,

accurate prediction of heart failure is very important

to prevent heart failure. In this context, many scholars

324

Zhang, H.

Comparison of Prediction Models for Heart Failure Related Data.

DOI: 10.5220/0013825200004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 324-330

ISBN: 978-989-758-774-0

have used machine learning methods for more

accurate prediction.

Scholars such as Javeed Ashir et al. have utilized

machine learning to predict heart failure (Javeed et

al., 2022). They analyzed the study using different

mechanical models. These include, but are not

restricted to, Random Forest (RF), logistic regression,

support vector machines (SVM), convolutional

neural networks (CNN), and recurrent neural

networks (RNN). To decrease data dimensionality

and increase model accuracy, they also use a variety

of approaches (principal component analysis (PCA),

independent component analysis (ICA), etc.) to

extract and choose important features. This paper

summarizes several public datasets, such as

University of California, Irvine (UCI) Heart Disease

dataset, Cleveland dataset, StatLog dataset, etc.

Accuracy, Sensitivity, Specificity and other

indicators were used to evaluate the model

performance.

However, the role of machine learning in self-

management for heart failure patients has not been

adequately explored. Sheojung and many other

scholars compared ML and statistical regression

models for predicting prognosis of heart failure

patients. They believe that ML methods have more

advantages than statistical regression models.

Because ML method gets higher c-indices. However,

from the perspective of epidemiological evaluation of

clinical prediction models, the quality of currently

available ML-based prediction models remains

suboptimal (Shin et al., 2019).

This research compares the accuracy differences

of K-Nearest Neighbors, Random Forest, and

Logistic Regression models in predicting heart

failure. This study aims to provide insights and

references for heart failure research and treatment.

2 METHODOLOGY

2.1 Data Source

The data used in this study were obtained from

Kaggle. The data set used in this study is called the

Heart Failure Prediction Data Set and is owned by

Larxel. This dataset has been widely used in the field

of healthcare research, especially related to heart

failure prediction and analysis.

This dataset received a usability rating of 10.0,

indicating its high quality and reliability for research

purposes. It was downloaded 158994 times, reflecting

its popularity and usefulness among researchers and

practitioners. This dataset contains records from 299

participants and includes 12 clinical characteristics

such as age, sex, ejection fraction, serum creatinine,

and other relevant health measures. These

characteristics are commonly used in medical studies

to predict outcomes such as mortality or readmission

rates in patients with heart failure.

This dataset is particularly valuable for machine

learning and statistical modeling studies because it

provides a comprehensive set of clinical variables that

can be used to train and evaluate predictive models.

In addition, the structure and variables of the dataset

are very consistent with the objectives of this study.

2.2 Variables and Data Preprocessing

In the original dataset, there were 12 variables, and

the names and explanations of each variable are

shown in Table 1.

For data preprocessing, the normal range of serum

sodium is defined in medicine as 135-145 mEq/L.

Python code was used to remove outliers that fall

outside this range. This operation removes 15 rows of

serum sodium data with no more than 20% missing

values. At the same time, no variable in this paper has

more than 20% missing value, so there is no need to

reduce the variable.

The original dataset contains 12 clinical features,

which may introduce complexity and redundancy into

the prediction model. High dimensional data can lead

to overfitting, especially when some features exhibit

multicollinearity or weak correlation with the target

variable, DEATH_EVENT. Principal Component

Analysis (PCA) is used in this research to overcome

this problem by reducing the dimension while

keeping important information.

2.3 Machine Learning Models

Three models-the K-Nearest Neighbor model, the

Random Forest model, and the Logistic Regression

model-were employed for analysis in this work.

The logistic function is used by the logistic

regression model to simulate the likelihood of a

particular class or occurrence (Li, 2021). The formula

is given by:

𝑃



𝑌=1

𝑋































⋯









(1)

Where β



is the intercept, and β



,β



,…,β



are the

coefficients for the input features 𝑋



,𝑋



,…,𝑋



During training, a large number of decision trees

are constructed using an ensemble learning approach

called Random Forest, which independently

generates the mean prediction of each tree.

Comparison of Prediction Models for Heart Failure Related Data

325

Table 1: Attribute Information

Variables Explanation

Appendix

age Age of the patient

anaemia Whether the patient has anaemia

1 for yes, 0 for no

creatinine_phosphokinase Blood level of the CPK enzyme

diabetes Whether the patient has diabetes

1 for yes, 0 for no

ejection_fraction The proportion of blood that exits the heart

high_blood_pressure Whether the patient has hypertension

1 for yes, 0 for no

platelets Blood platelet count

serum_creatinine Level of serum creatinine in the blood

serum_sodium Level of serum sodium in the blood

Sex Gender of the patient

1 for male, 0 for female

Smoking Whether the patient smokes

1 for yes, 0 for no

time Duration of follow-up in days

DEATH_EVENT Whether the patient died

1 for yes, 0 for no

Each tree is trained on a random subset of the data.

Each tree is trained on a random sample of the data,

and at each split, a random subset of characteristics is

considered.

K-Nearest Neighbor is a non-parametric

regression and classification method. In both cases,

the k training examples that are closest to one another

in the feature space comprise the input. A class

membership is the result of categorization and is

decided by a majority vote of its neighbors. The

average of its neighbors' values is the result of

regression. The formula for the prediction is:

𝑦=





∑

𝑦







(2)

Where 𝑦



are the values of the K-Nearest Neighbors.

3 RESULTS AND DISCUSSION

3.1 Data Distribution

Figure 1 represents the histogram of the frequency

distribution of the 7 principal components. “Age” is

close to a normal distribution centered on the mean

age (60-70). There was a slight rightward deviation of

“platelets”, indicating an elevated platelet count in a

subset of patients. “Time” is clustered around the

median and the surface observation period is

balanced. Notably, “creatinine_phosphokinase”

showed a strong right skew, reflecting elevated

muscle or myocardial damage in a few cases.

“Serum_ creatinine” showed an extreme right

distribution, suggesting serious problems with renal

function in high-risk patients. “Ejection_fraction”

was left skewed due to reduced systolic function. The

close aggregation of “serum_sodium” confirmed the

rationality of the clinical values.

3.2 Logistic Regression Model

Table 2 represents the Variance Inflation Factor (VIF)

values. VIF is used to measure the strength of linear

correlation between independent variables, with

higher values indicating more severe collinearity. The

VIF value of "sex" is 2.75, which is the highest among

all features, but it is still in the safe range. The VIF

values of features in the table are all low, indicating

that each feature has good independence and is

suitable for direct use in logistic regression models.

Table 2: Components’ VIF Value

Feature VIF

e 1.079

anaemia 1.514

creatinine

hos

hokinase 1.075

diabetes 1.408

ection

fraction 1.045

high_blood_pressure 1.393

latelets 1.055

serum_creatinine 1.024

serum

sodiu

1.023

sex 2.749

Smoking

time

2.067

1.076

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

326

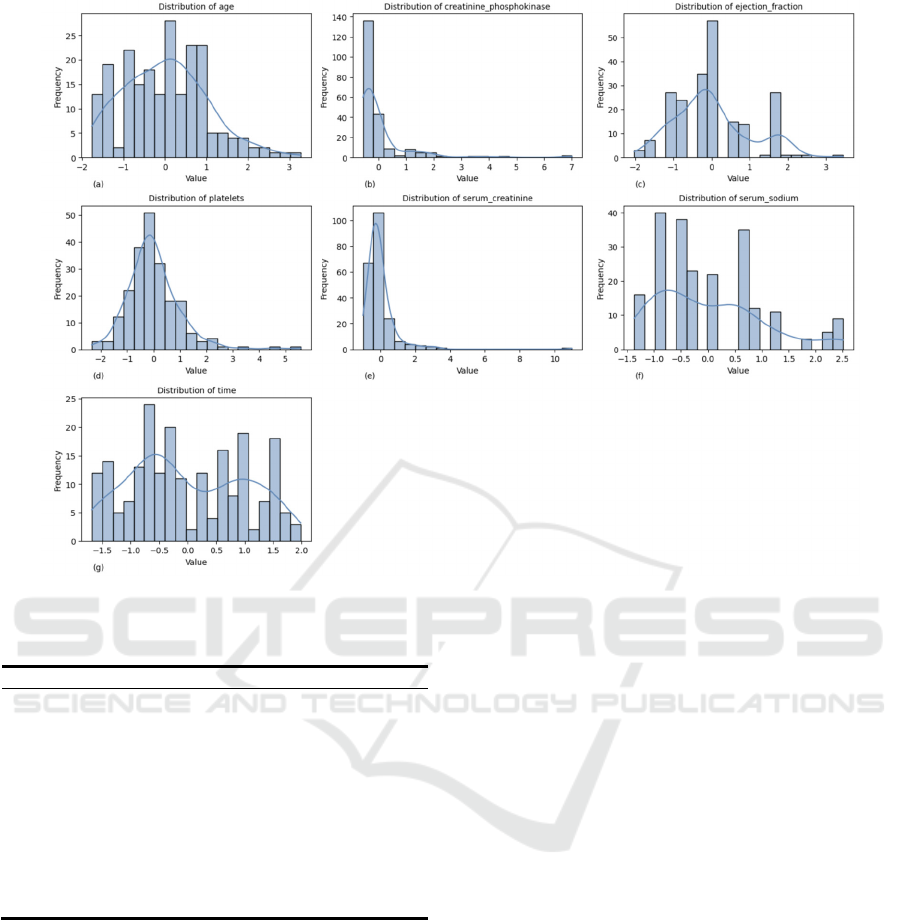
Figure 1: Histograms of the variable (Picture credit: Original)

Table 3: Logistic Regression Coefficient

Feature Coefficient

Interce

t -0.806

c1 -0.276

c2 0.723

c3 1.046

c4 -0.959

c5 -0.365

pc6

pc7

0.372

0.504

0.941

pc9

c10

-0.477

-0.428

Table 3 represents the coefficients of each principal

component in the logistic regression model the impact

and strength of patient death. When all principal

components (pc1-pc10) are zero, the benchmark log

probability of the event is -0.806. This represents the

initial probability of an event occurring in the overall

data. Through observation, it can be found that pc3

(1.046) and pc8 (0.941) are strong positive driving

factors. pc4 (-0.960) is a strong negative driving

factor. The absolute values of the coefficients of pc1,

pc5, pc9, and pc10 are small (<0.5) and have a weak

impact on the results. Therefore, it can be concluded

that high serum creatinine and aging are the main

drivers of mortality risk, and the model results are

consistent with medical knowledge.

The confusion matrix generated by the established

model's predictions on the test set is shown in Figure

2. The computed accuracy is 0.791, meaning that the

model has an accuracy of around 79.07% for all

predictions. With a precision rate of 0.429, 42.86

percent of the instances that the model projected

would result in deaths are accurate. With a recall rate

of 0.857, the model was able to correctly identify

85.71% of the real fatalities. The accuracy rate and

recall rate performance are combined to get the F1

score of 0.571.

The confusion matrix shows that while the model

accurately forecasted 28 cases in which no death

event happened (TN), it mispredicted eight events as

deaths (FP). For the cases where a death event

occurred, the model correctly predicted six (TP), but

one was incorrectly predicted as no death (FN). It can

be concluded that the model performs well in

identifying actual death events but needs to be

improved in reducing false positives. In conclusion,

the model performed reasonably well in predicting

heart failure deaths, but there is still room for

improvement.

Comparison of Prediction Models for Heart Failure Related Data

327

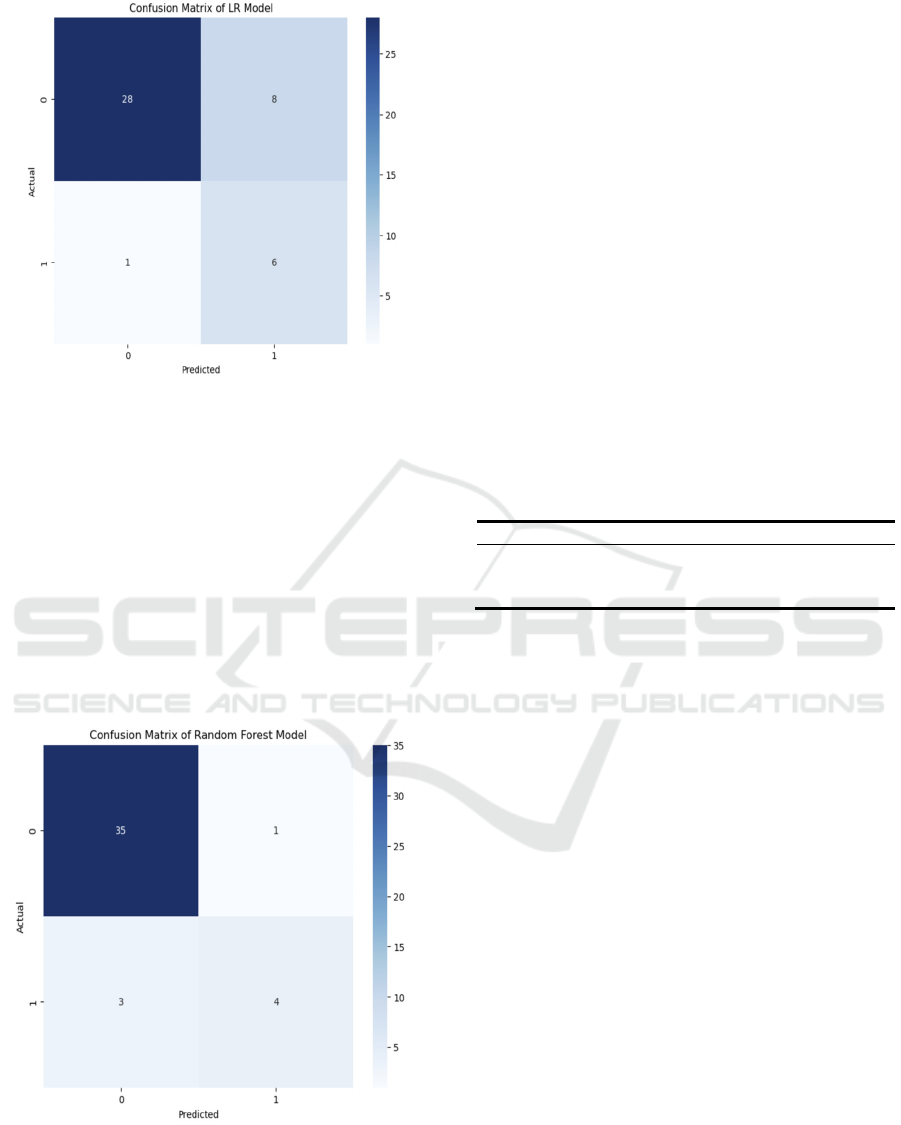
Figure 2: Confusion Matrix of LR Model (Picture credit:

Original)

3.3 Random Forest Model

Figure 3 represents the random forest model. Through

the model, the accuracy is 0.9070, indicating that the

model has a correct rate of about 90.70% in all

predictions. The precision rate of 0.800 means that

the model is correct in 80% of the cases predicted as

deaths. The recall rate is 0.571, indicating that the

model successfully identified 57.14% of the actual

deaths. The F1 score is 0.667, which combines

performance of precision and recall.

Figure 3: Confusion Matrix of RM (Picture credit: Original)

The confusion matrix demonstrates how well the

random forest model predicts the incidence of heart

failure deaths. The model correctly predicted 35 cases

with no death event (TN) and only one case was

incorrectly predicted as death (FP). For the cases

where a death event occurred, the model correctly

predicted four (TP), but three were incorrectly

predicted as no death (FN).

Overall, the model performs well in identifying

cases where no death event occurred, but there is

room for improvement in identifying actual deaths.

3.4 K-Nearest Neighbor Model

Table 4 shows the cross-validation table. In the

experiment, three k values of 5, 7 and 9 were selected.

The cross-validation results show that when k=5, the

average accuracy of the model is 0.766, which is the

highest value among the three test k values (5, 7, 9).

This shows that in multiple data divisions, the

performance of the model when k=5 is the most stable

and reliable.

Table 4: Resampling Results Across Tuning Parameters

Accurac

5 0.7663

7 0.7605

9 0.7549

The confusion matrix for the K-Nearest Neighbor

Model is shown in Figure 4. The confusion matrix

shows the model's accurate classification

performance on the test set. With an accuracy of

0.814, the model's efficacy under a particular data

partition is demonstrated. The matrix's values for

TP=2, TN=33, FP=3, and FN=5 show that the model

does a good job of recognizing the negative class

(non-events), but it makes some mistakes when

identifying the positive class (events). The precision

rate is 0.400, the recall rate is 0.286, and the F1 score

is 0.33. Despite the high accuracy, there is still room

for improvement in the performance of the model in

identifying positive classes.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

328

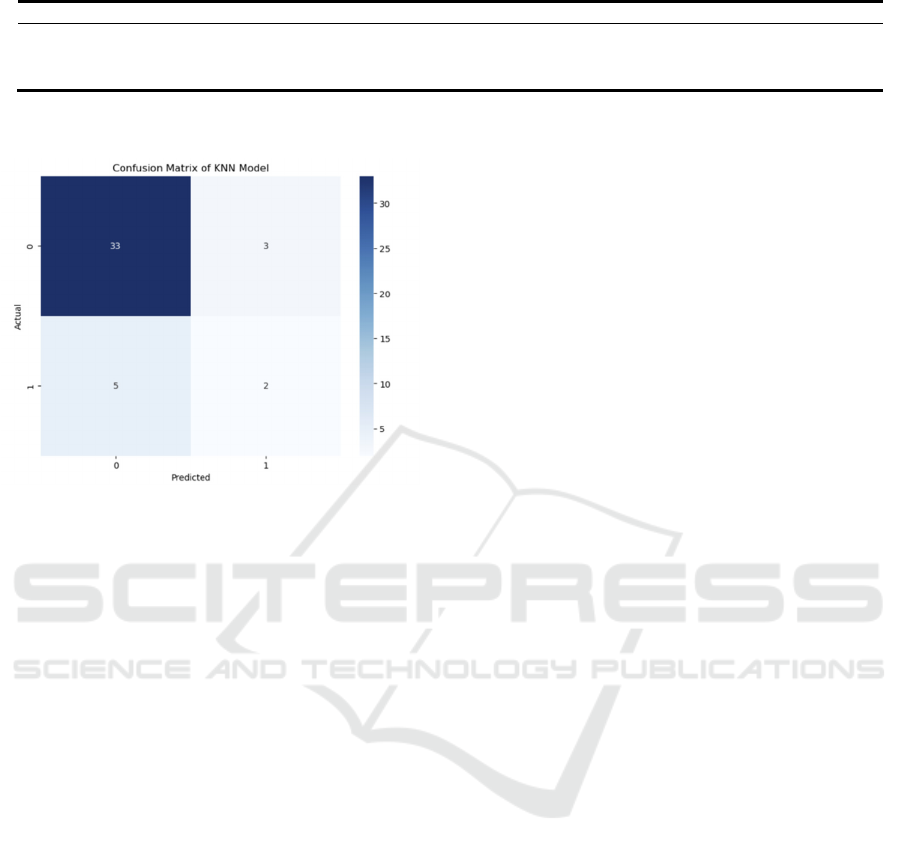
Table 5: Prediction Accuracy

Accurac

Precision Recall F1 Score

Logistic Regression 0.791 0.429

0.857 0.571

Random Forest 0.907 0.800 0.571 0.667

K-Nearest Neighbor 0.814 0.400 0.286

0.333

Figure 4: Confusion Matrix of KNN (Picture credit:

Original)

In evaluating the KNN model, this paper combines

both methods of confusion matrix and cross

validation. By combining both techniques, this paper

can both guarantee the accuracy of model selection

and learn more about how the model functions with

real data. While the accuracy of the confusion matrix

illustrates the model's impact on a particular test set,

the accuracy of cross-validation indicates the model's

capacity for generalization. These two techniques

enable people to evaluate the model's performance in

detail and present strong justifications for its

application.

3.5 Comparison

As can be seen from Table 5, this paper has found that

Random Forest is best model in predict heart failure

field.

Advantages: RF model has the advantage of high

accuracy and robustness. It is more effective in

dealing with high-dimensional data.

Disadvantages: RF model has a large amount of

calculation and slow operation speed. Moreover, the

model is relatively unintuitive and not easy to

understand.

4 CONCLUSION

In order to predict mortality events associated to heart

failure, this study examined the effectiveness of three

machine learning models: K-Nearest Neighbor,

Random Forest, and Logistic Regression. According

to the results, the Random Forest model had the best

prediction performance on the test set, with the

greatest accuracy of 0.907. This implies that the

Random Forest model is especially appropriate for

this dataset, most likely as a result of its proficiency

in managing intricate nonlinear connections and

feature interactions.

While the Random Forest model excels in

accuracy and robustness, it also presents challenges

such as high computational load and slower operation

speed. Additionally, the model's lack of intuitiveness

may pose interpretability issues in clinical settings.

Extending experimental samples should be the

main goal of future studies in order to improve the

findings' generalizability. Enhanced feature selection

techniques could further refine the models by

reducing dimensionality and minimizing redundancy.

Moreover, combining more mixed models or hybrid

approaches could potentially improve prediction

accuracy and address the limitations of individual

models.

There is great potential for improving diagnostic

effectiveness and facilitating individualized treatment

planning through the use of machine learning into

clinical procedures. Healthcare professionals may

prioritize high-risk patients for early intervention by

precisely predicting the consequences of heart failure,

which might improve patient outcomes and save

healthcare expenditures. Further research into model

interpretability and computational efficiency is also

warranted to ensure that these models are practical

and accessible for real-world clinical applications.

REFERENCES

Forouzanfar, M. H., Afshin, A., Alexander, L. T., Anderson,

H. R., Bhutta, Z. A., Biryukov, S., et al. 2017. Global,

regional, and national burden of cardiovascular diseases

for 10 causes, 1990–2015: A systematic analysis for the

Comparison of Prediction Models for Heart Failure Related Data

329

Global Burden of Disease Study 2015. The Lancet,

389(10075), 1599-1609.

Ho, K. K., Anderson, K. M., Kannel, W. B., Grossman, W.,

Levy, D. 1993. Survival after the onset of congestive

heart failure in Framingham Heart Study subjects.

Circulation, 88(1), 107-115.

Javeed, A., Khan, S. U., Ali, L., Ali, S., Imrana, Y., Rahman,

A., Asghar, M. Z. 2022. Machine learning-based

automated diagnostic systems developed for heart

failure prediction using different types of data

modalities: A systematic review and future directions.

Computational and Mathematical Methods in Medicine,

9288452.

Khan, M. S., Sreenivasan, J., Lateef, N., Abougergi, M. S.,

Greene, S. J., Ahmad, T., et al. 2021. Trends in 30- and

90-day readmission rates for heart failure. Circulation:

Heart Failure, 14(6), 450-458.

Li, J. 2021. Analysis of the dynamic positioning system of

a 152000 heavy duty shuttle oil tanker. Ship and Ocean

Engineering, 37(05), 56-59.

Norhammar, A., Bodegard, J., Vanderheyden, M., Tangri,

N., Karasik, A., Maggioni, A. P., et al. 2023. Prevalence,

outcomes and costs of a contemporary, multinational

population with heart failure. Heart, 109(6), 548-556.

Retrum, J. H., Boggs, J., Hersh, A., Wright, L., Main, D. S.,

Magid, D. J., et al. 2013. Patient-identified factors

related to heart failure readmissions. Circulation:

Cardiovascular Quality and Outcomes, 6(2), 171-177.

Rockwell, J. M. 1999. Heart failure. The American Journal

of Nursing, 99(10), 24BB–24HH.

Savarese, G., Becher, P. M., Lund, L. H., Seferovic, P.,

Rosano, G. M. C., Coats, A. J. S. 2023. Global burden

of heart failure: A comprehensive and updated review of

epidemiology. Cardiovascular Research, 118(10),

3272-3287.

Shin, S., Freitas, C., Abdel-Qadir, H. M., Mahendiran, M.,

Tomlinson, G. A., Epelman, S., Lawler, P. R., Billia, F.,

Gramolini, A., Austin, P. C., Ross, H. J., Lee, D. S. 2019.

Comparison of machine learning methods with

statistical regression models for prediction of

readmission and mortality in heart failure patients: A

systematic review. Circulation, 140, 12533.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

330