
Research Report on Resonant Tunneling Effect in Double-Barrier
Structures
Chengrui Tang
a
Institute for Advanced Study, Shenzhen University, Shenzhen, 518060, China
Keywords: Resonant Tunneling Effect, Double-Barrier, TMM.
Abstract: This study systematically investigates the resonant tunneling effect and transmission characteristics of double-
barrier structures through theoretical analysis and numerical simulations. Based on the Schrödinger equation
under the effective mass approximation, analytical expressions for the transmission coefficient and resonance
conditions are derived, revealing that resonance energy levels are dominated by quantum well coupling effects.
The transmission spectrum is proven to exhibit a Lorentzian-shaped distribution near resonance energies.
Further numerical calculations using the transfer matrix method (TMM) validate the conservation of
probability (T + R ≈ 1) and demonstrate a single dominant resonance peak (T > 0.9). The results indicate that
barrier height (V₀), barrier width (w), and well width (d) significantly influence the position and width of
resonance peaks, providing a theoretical foundation for optimizing resonant tunneling devices. By combining
analytical derivations with numerical verification, this work deepens the understanding of electron transport
mechanisms in multi-barrier quantum structures, offering potential applications in high-speed electronic
devices and quantum engineering.
1 INTRODUCTION
Quantum tunneling is a hallmark phenomenon of
quantum mechanics. It distinguishes quantum
mechanics from classical physics by enabling
microscopic particles to traverse potential barriers
that exceed their energy. This effect is not only a
fundamental prediction of quantum theory (such as
Gamow’s theory of alpha decay) but also the core
physical principle behind modern nanoelectronic
devices. From the atomic-scale resolution of
scanning tunneling microscopes to the terahertz
(THz) rectification in triple-barrier resonant
tunneling diodes with on-chip antennas, quantum
tunneling has continuously redefined the frontiers of
device physics (Arzi et al., 2019).
The phenomenon of quantum tunneling, where
particles traverse classically forbidden energy
barriers via wavefunction penetration, serves as the
foundational mechanism driving the functionality of
engineered multi-barrier heterostructures. Recent
advancements in multi-barrier heterostructures reveal
a rich interplay between quantum confinement and
a
https://orcid.org/0009-0008-7332-9081
transport dynamics. For instance, asymmetric
barrier–well–barrier structures employing
ferroelectric HfO₂ layers demonstrate a 200%
enhancement in tunneling electroresistance (TER)
under electric field modulation, providing a non-
volatile memory mechanism that outperforms
traditional memristive devices (Chang and Xie,
2023). Concurrently, resonant tunneling in
ZnO/In₂O₃ heterojunctions has enabled room-
temperature NO₂ gas detection with sub-ppm
sensitivity, where quantum well coupling
dynamically regulates charge carrier mobility
through selective barrier penetration—a paradigm
shift in solid-state sensing (Liang et al., 2021). In
terms of resonant tunneling diodes, a terahertz
coherent receiver using a single resonant tunnelling
diode and optimum device parameters to attain the
highest peak-to-valley current ratio (PVCR) in
resonant tunneling diodes was proposed (Nishida et
al., 2019; Ipsita, Mahapatra, Panchadhyayee, 2021).
The exploration of tunneling mechanisms now
extends beyond conventional semiconductors. In
metallic multi-quantum-well systems, resonant
Tang, C.
Research Report on Resonant Tunneling Effect in Double-Barrier Structures.
DOI: 10.5220/0013824400004708
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 291-294
ISBN: 978-989-758-774-0
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
291

inelastic tunneling spectroscopy has uncovered an
energy-selective hot carrier injection pathway,
enabling precise control over plasmonic energy
conversion efficiencies by exploiting subband
coupling in stacked metal-insulator interfaces (Zhang
et al., 2023). Meanwhile, pseudospin-1 Dirac–Weyl
fermion systems exhibit spin-momentum-locked
resonant tunneling channels, where quantized
conductance plateaus emerge from the interplay
between chiral pseudospin textures and double-
barrier potentials—a phenomenon that challenges
classical scattering theory and opens avenues for
topological quantum devices (Zhu, 2024).
The resonant tunneling effect is a significant
phenomenon in quantum mechanics, particularly in
semiconductor heterostructure devices such as
resonant tunneling diodes. As the simplest multi-
barrier system, the study of resonant tunneling in
double-barrier structures lays the foundation for
understanding more complex multi-barrier systems
(Xu et al., 1991). This study combines numerical
simulations and theoretical analysis to investigate the
transmission coefficient, resonance conditions, and
spectral features of double-barrier structures,
elucidating their physical principles and device
potential.
2 THEORETICAL MODEL
2.1 Derivation
Consider a double-barrier structure composed of two
barriers with height 𝑉
and thickness 𝐿
, and a well
with width 𝐿
. The electron energy 𝐸 satisfies 0<
𝐸<𝑉
, with electrons incident from the left and
tunneling through the barriers to the right. The
wavefunction in each region obeys the effective mass
Schrödinger equation:
−
ℏ
∗
+ 𝑉(𝑥)𝜓=𝐸𝜓, (1)
where 𝑚
∗
is the effective mass, ℏ is the reduced
Planck’s constant, 𝜓 is the electron wave function.
The potential distribution is:
𝑉(𝑥) =
0 (incident region),
𝑉
(barrier regions),
0 (well region),
𝑉
(right barrier region).
(2)
The continuity of the wavefunction and its first
derivative at the boundaries is solved using the
transfer matrix method. The transmission coefficient
𝑇 is derived as (Tsu, 1973; Kane, 1969):
𝑇=
1+
(
𝐴𝐻
)
, (3)
where:
𝐴=
sinh (𝑘
𝐿
), (4)
𝐻=2cosh (𝑘
𝐿
)cos (𝑘
𝐿
)−
sinh (𝑘
𝐿
)sin (𝑘
𝐿
), (5)
with 𝑘
=
√
2𝑚
∗
𝐸/ℏ and 𝑘
=
2𝑚
∗
(𝑉
−𝐸)/
ℏ.
When 𝐻=0, the transmission coefficient 𝑇=1,
indicating complete resonant tunneling. The
resonance energy 𝐸
approximates the quantized
energy level of the well, demonstrating that
resonance levels are determined by the bound states
of the well. At this condition, the electron
wavefunction forms a standing wave in the well,
maximizing tunneling probability.
Near the resonance energy 𝐸
, the transmission
coefficient follows a Lorentzian distribution:
𝑇≈1+
,
(6)
where the full width at half maximum (FWHM)
Δ𝐸=𝐴(𝐸
)
|
reflects the sharpness of
the resonance. A smaller Δ𝐸 corresponds to a longer
resonance lifetime.
2.2 Physical Implications
In terms of quantum well coupling, the finite barrier
height couples the quantized energy levels of the well
to the external environment, causing resonance
energies to deviate slightly from the eigenvalues of
an isolated well. For applications, the high selectivity
of Lorentzian-shaped transmission spectra is
valuable for high-speed electronic devices (e.g.,
terahertz oscillators) and quantum computing.
3 NUMERICAL METHODS
A double-barrier structure is defined by two barriers
(𝑉
=0.3 eV, 𝑤=2 nm) and a well (𝑑=5 nm).
Electrons with energy 0<𝐸<𝑉
tunnel through the
barriers, governed by the effective mass Schrödinger
equation.
The transfer matrix method (TMM) is employed
to compute transmission ( 𝑇 ) and reflection ( 𝑅 )
coefficients:
First calculate wavevector and determine 𝑘
(real
for propagating waves, imaginary for evanescent
waves) based on 𝐸 and 𝑉
.
𝑘
=
2𝑚
∗
(𝐸− 𝑉
)/ℏ (𝐸>𝑉
)
𝑖
2𝑚
∗
(𝑉
−𝐸)/ℏ (𝐸<𝑉
)
(7)
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
292

where 𝑗=1,2,3,4,5 corresponds to the five
regions (left incident region, left barrier, well, right
barrier, right exit region). Evanescent waves
(Im(𝑘) 0) dominate in barrier regions when 𝐸<
𝑉
. Then, construct interface matrices enforcing
wavefunction continuity at boundaries. For each
interface between regions 𝑗 and 𝑗+1, the interface
matrix is derived from boundary conditions:
𝑀
→
=
11
𝑘
−𝑘
11
𝑘
−𝑘
(8)
And propagation Matrices account for model
phase accumulation in barriers and wells.
Propagation matrices incorporate phase evolution
across each region:
𝑀
propagate,
=
𝑒
0
0𝑒
(9)
Finally, multiply matrices sequentially to derive
𝑇=|𝑡|
and 𝑅=|𝑟|
and validate 𝑇+𝑅=1 to
complete the conservation check.
4 RESULTS AND DISCUSSIONS
Figure 1 shows 𝑇 and 𝑅 versus energy, meaning
when the electron energy approaches the quantized
energy level of the potential well, 𝑇≈1 and 𝑅≈0,
indicating perfect resonant tunneling and the
appearance of resonant peaks. The transmission peak
near 𝐸
matches theoretical predictions, with FWHM
Δ𝐸 dependent on barrier parameters.
Figure 1: Quantum Tunneling in Double Barrier Structure:
𝑉
=0.3 eV,𝑤=2 nm,𝑑=5 nm(Picture credit:
Original).
Figure 2 shows with the increase of the barrier
height V₀, the formant moves towards the high
energy direction and the peak width Narrows. This is
because the higher barrier enhances the quantization
effect of the quantum well, making the electrons
more tightly bound in the potential well, resulting in
higher resonance energy and narrower formant.
Figure 2: 𝑉
=0.4 eV,𝑤=2 nm,𝑑=5 nm(Picture
credit: Original)
Figure 3 shows an increase in the barrier width
enhances the quantum confinement effect, bringing
the resonance energy closer to the eigenvalue of the
isolated potential well. This is because the wider
barrier limits the movement of electrons in the lateral
direction, resulting in a more pronounced split of the
quantized energy levels, thus bringing the resonance
energy closer to the eigenvalue of the isolated
potential well.
Figure 3: 𝑉
=0.3 eV,𝑤=3 nm,𝑑=5 nm(Picture
credit: Original)
Figure 4 shows that the increase of the potential
well width will reduce the quantized energy level
spacing, which may lead to the appearance of the
multi-peak structure. This is because a wider
potential well provides more room for electrons to
move, making the distribution of quantized energy
levels more dense, resulting in multiple formants in
the transmission spectrum.
Figure 4: 𝑉
=0.3 eV,𝑤=2 nm,𝑑=8 nm(Picture
credit: Original)
Figure 5 confirms 𝑇+𝑅=1 in above cases,
ensuring numerical consistency and wavefunction
integrity. The verification of probability conservation
is an important part of numerical simulation, which
not only ensures the physical rationality of the
calculated results, but also provides a reliable
numerical reference for the subsequent experimental
research and device design, and enhances the
reliability of the research results.
Research Report on Resonant Tunneling Effect in Double-Barrier Structures
293
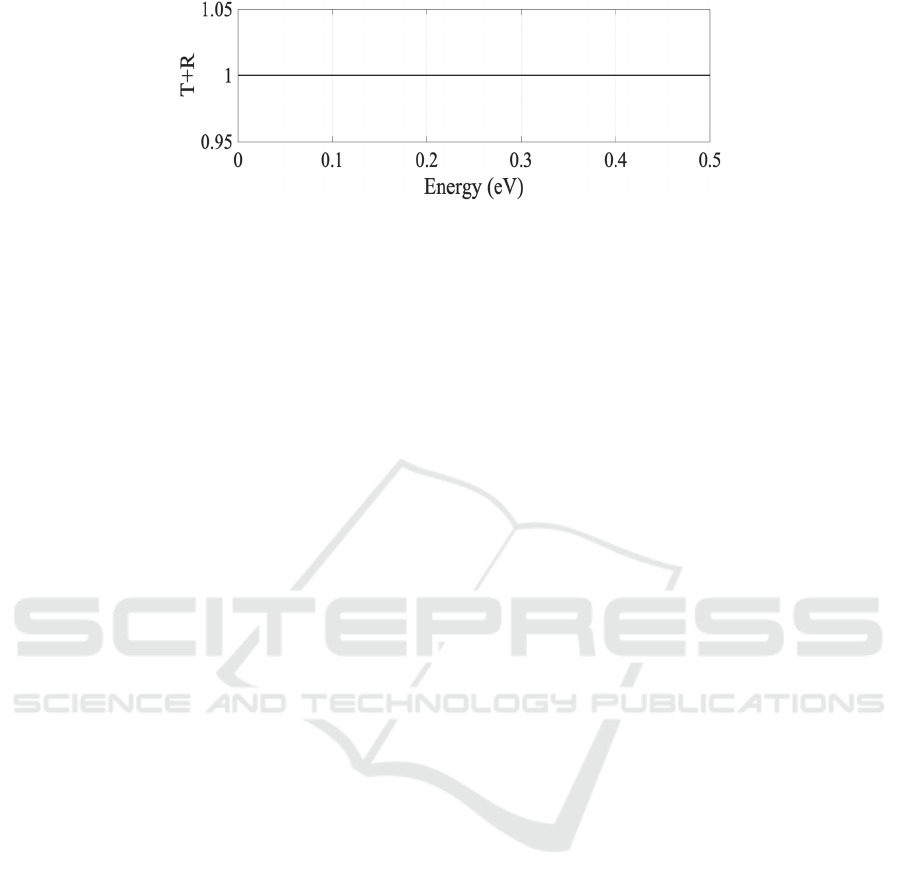
Figure 5: Probability Conservation (Picture credit: Original)
5 CONCLUSION
In conclusion, the research analyzes the transmission
coefficient, resonance conditions, and spectral
features of double-barrier structures, elucidating their
physical principles. The resonance condition for
double-barrier structures is determined by 𝐻=0,
with resonance energies approximating the quantized
levels of the well. The transmission spectrum near
resonance energies exhibits a Lorentzian profile, with
FWHM strongly dependent on barrier parameters.
Numerical simulations validate resonant tunneling in
double-barrier structures, with Lorentzian
transmission spectra aligning with theory. The TMM
accurately computes 𝑇 and 𝑅 while preserving
probability conservation. Resonance characteristics
are tunable via barrier/well parameters, enabling
tailored device design and the performance of the
device can be optimized. This provides a broad
prospect for the development of new high-speed
electronic devices and quantum engineering
applications. However, one limitation about the
research is that the current model assumes elastic
tunneling and ideal rectangular barriers, neglecting
inelastic scattering effects (e.g., electron-phonon
coupling) and interface roughness, which may lead to
deviations in high-bias or high-temperature regimes.
Incorporating non-equilibrium Green ’ s function
(NEGF) or time-dependent density functional theory
(TDDFT) to account for inelastic scattering and
defect-mediated tunneling, enhancing predictive
accuracy under non-ideal conditions is necessary for
future improvement work.
REFERENCES
Arzi, K., Clochiatti, S., Suzuki, S., Rennings, A., Erni, D.,
Weimann, N., Asada, M., Prost, W., 2019. Triple-
barrier resonant-tunnelling diode THz detectors with
on-chip antenna. In 2019 12th German Microwave
Conference (GeMiC), Stuttgart, Germany, pp. 17–19.
Chang, P., Xie, Y., 2023. Ferroelectric tunnel junction
based on asymmetric barrier–well–barrier structure:
the role of resonant tunneling. IEEE Transactions on
Electron Devices, 70(5), 2282–2290.
Ipsita, S., Mahapatra, P.K., Panchadhyayee, P., 2021.
Optimum device parameters to attain the highest peak
to valley current ratio (PVCR) in resonant tunneling
diodes (RTD). Physica B: Condensed Matter, 611,
412788.
Kane, O.E., 1969. Tunneling Phenomena in Solids. Plenum
Press.
Liang, X., Zhang, J., Du, L., Zhang, M., 2021. Effect of
resonant tunneling modulation on ZnO/In₂O₃
heterojunction nanocomposite in efficient detection of
NO₂ gas at room temperature. Sensors and Actuators
B: Chemical, 329, 129230.
Nishida, Y., Nishigami, N., Diebold, S., Kim, J., Fujita, M.,
Nagatsuma, T., 2019. Terahertz coherent receiver using
a single resonant tunnelling diode. Scientific Reports,
9, 18125.
Tsu, R., Esaki, L., 1973. Tunneling in a finite superlattice.
Applied Physics Letters, 22(11), 562–564.
Xu, H., Wang, Y., Zhang, F., Chen, G., 1991. Resonant
tunneling condition in ABCBA–type rectangular
double–barrier structures. Physica Status Solidi B:
Basic Solid State Physics, 163.
Zhang, Y., Lepage, D., Feng, Y., Zhao, S., Chen, H., Qian,
H., 2023. Resonant inelastic tunneling using multiple
metallic quantum wells. Nanophotonics, 12(16), 3313–
3321.
Zhu, R., 2024. Transport properties of the resonant
tunneling structures based on the pseudospin-1 Dirac–
Weyl fermions. Physica B: Condensed Matter, 687,
416091.
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
294
