A Comparative Study on Central Projection and Parallel Projection

Lily Yiting Huang

Hubei Wuchang Experimental High School, Wuhan, 430061, China

Keywords: Parallel Projection, Central Projection, Perspective Transformation, Descriptive Geometry, Computer

Graphics.

Abstract: A comprehensive comparative study focusing on central projection and parallel projection is conducted in

this paper. The two projection methods are systematically analysed from multiple perspectives including their

physical definitions, fundamental principles, mathematical theorems, geometric properties, algorithmic

implementations, and practical applications. The differences and connections between the two projections are

elucidated in detail. Their advantages and disadvantages across various disciplines are also explored, and the

study of an application example is given. It is demonstrated that central projection, which simulates human

visual perception, provides more realistic scene perception and is suitable for visual arts production field, but

non-linear transformations and more complex computation are involved, leading to an inaccurate geometric

measurement. In contrast, parallel projection preserves geometric proportions through linear transformations

with simpler computations, but lacks spatial depth perception, rendering it ideal for precision-dependent fields

such as measurement and manufacturing. Finally, the application of integration on central projection and

parallel projection methods and their development in the future are explored. This study provides valuable

references and insights for related research fields.

1 INTRODUCTION

Projection is the process of mapping a three-

dimensional object in space onto a two-dimensional

plane. The shadow formed by light rays illuminating

an object and casting onto a screen behind it is

referred to as a projection. Central projection and

parallel projection are two fundamental methods of

projection theory, widely applied in fields such as

geometry, computer graphics, engineering drafting,

photography, painting, and artistic creation (Müller,

et al., 2021; Liu et al., 2024; Garcia et al., 2019). Due

to their distinct definitions and principles, these two

projection methods exhibit different characteristics

and are suited to different scenarios. However, they

both play important roles in practical applications.

This paper conducts a comparative study of these two

projection methods by analysising their physical

definitions and principles, geometric and

mathematical properties, computational approaches,

and application feilds. Furthermore, their future

development prospects are explored.

https://orcid.org/0009-0000-6110-3853

2 DEFINITIONS, PRINCIPLES,

AND CHARACTERISTICS

The essence of projection is transmitting the contours

of an object onto a designated plane through a set of

light rays (projection lines). Therefore, three essential

elements are required to form a projection. The fisrt

factor is projection center that can be regarded as the

light source. For instance, in the case of a shadow cast

by sunlight, the sun serves as the projection center.

The second is projection object that is being

projected. It may consist of geometric elements such

as points, lines, or surfaces, or a three-dimensional

solid. The third is projection plane, a receiving

surface where the image is formed after the light rays

pass through the object. It can be a ground surface, a

wall, a drawing sheet, etc.

The spatial position of the projection center and

the direction of the projection lines influence the

shape and size of the projected image on the plane.

Based on the mutual relationships between projection

lines, projections are classified into central projection

Huang, L. Y.

A Comparative Study on Central Projection and Parallel Projection.

DOI: 10.5220/0013822100004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 205-212

ISBN: 978-989-758-774-0

205

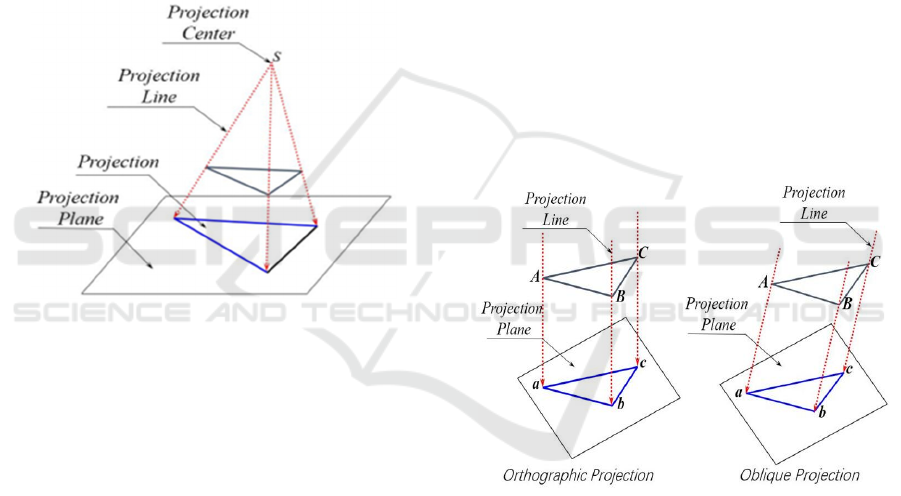
(perspective projection) and parallel projection

(Foley et al., 2018; Coxeter et al., 2003).

2.1 Central Projection

Central projection refers to a projection method in

which light rays emanate from a single point (the

projection center) and diverge radially, passing

through an object and intersecting a receiving surface

to form a perspective relationship. Geometrically, this

process involves extending the lines connecting each

point on the object to a fixed projection center until

they intersect a plane that does not contain the

projection center. The set of intersection points

constitutes the central projection of the object onto

that plane, as illustrated in figure 1.

Figure 1: Central Projection (Picture credit: Original).

In central projection, since all projection lines

converge at a single point (the projection center), the

varying distances between different parts of the object

and the projection center result in non-uniform

scaling, causing changes in the size and shape of the

projected image, whose actual dimensions and angles

may undergo nonlinear distortion (Carlson, 2003).

Parallel lines in the original object may intersect at

vanishing points on the projection plane, leading to

significant deviations between the projected image

and the original object. These Characteristics, to some

extent, compromise the metric accuracy of central

projection, limiting its widespread application in

classical solid geometry. However, the resulting

transformations enhance visual intuitiveness and

spatial realism, aligning with human visual

perception, e.g., near-far size attenuation.

Consequently, central projection is extensively

employed in artistic domains, such as painting and

photography, where it preserves a naturalistic

resemblance to the original object while emphasizing

depth and perspective (Peacock, 2001).

2.2 Parallel Projection

When the light source at the projection center is

relocated to infinity, all projection rays become

mutually parallel and intersect the projection plane at

a fixed angle, which is termed parallel projection. As

illustrated in figure 2, parallel projection can further

be categorized into two subtypes:

 Orthographic Projection

The projection lines are perpendicular to the

projection plane. For example, the standard

engineering multi-view drawings (including front,

top, and side views). This method preserves the true

dimensions and shapes of objects, making it

indispensable for technical drafting.

 Oblique Projection

The projection lines intersect the projection plane

at an oblique angle (90°). For example, cabinet

oblique projection which retains partial depth

perception exhibits less metric accuracy compared to

orthographic projection.

Figure 2: Parallel Projection (Picture credit: Original).

In parallel projection, the shape and size of objects

maintain proportional consistency on the projection

plane without scaling effects caused by varying

distances. Due to its superior metric properties,

relatively simple projection rules, and ease of

understanding and drafting, parallel projection is

broadly applied in fields requiring precise proportions

and resistance to perspective distortion. These

applications include engineering drawings,

mechanical manufacturing, cartography and

surveying, architectural design, and computer

graphics (Liu, 2022; Zhang et al, 2008; Luo et al.,

2009).

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

206

3 MATHEMATICAL THEOREMS

AND RELATED PROPERTIES

3.1 Fundamental Theorems and

Properties of Central Projection

 Collinearity Preservation

If three points in space lie on a straight line, their

central projections will remain collinear (or all

converge to points at infinity).

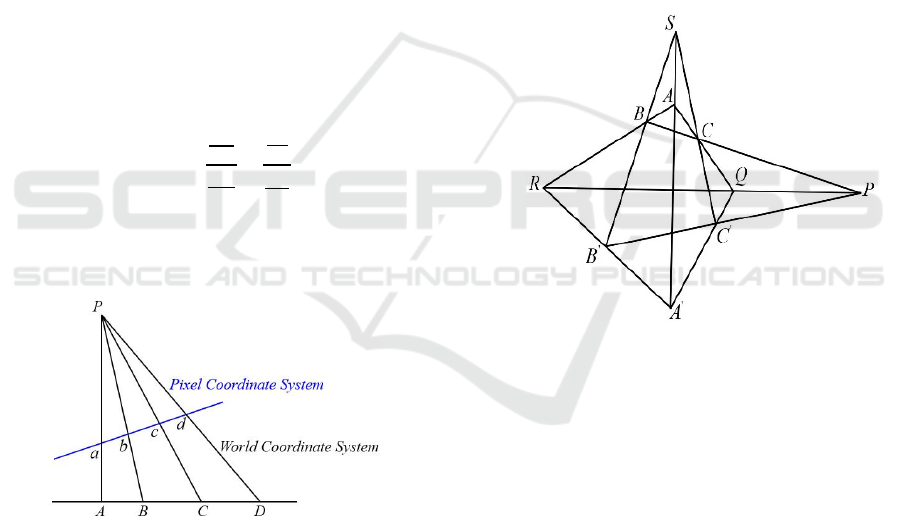
 Cross-Ratio Invariance

In central projection, the cross ratio of any four

collinear points remains invariant. This theorem holds

a central position in projective geometry and ensures

accurate proportional transformations in perspective

projection.

As illustrated in figure 3, four collinear points

𝐴,𝐵,𝐶,𝐷 are projected onto another line as 𝑎,𝑏,𝑐,𝑑

via central projection. While the lengths of projected

segments change and the ratios of individual

segments are not preserved, the cross ratio remains

invariant, that is:

(

𝐴

𝐵

，

𝐶𝐷

)

𝐶𝐴

𝐶𝐵

𝐷𝐴

𝐷𝐵

𝑐𝑎

𝑐𝑏

𝑑𝑎

𝑑𝑏

(1)

Here, all segments are treated as directed lengths with

signed magnitudes. Definitions of world coordinates

and pixel coordinates are provided in Section 4.

Figure 3: Cross-Ratio in Central Projection (Picture credit:

Original).

The cross-ratio invariance has significant

applications in computer vision, photogrammetry,

and robot navigation. Specific use cases include sun

positioning systems (based on shadow

measurements) (Zhang et al., 2015), structured-light

3D reconstruction (light-plane calibration) (Chen et

al., 2018), Camera self-calibration (using vanishing

points) (Cipolla et al., 1999).

 Nonlinearity

Central projection is not a linear transformation

(except when the projection center is at infinity, in

this case, it degenerates into parallel projection).

Notably, As introduced in Desargues’ theorem, in

homogeneous coordinates, central projection can be

represented as a fractional linear transformation.

 Non-Preservation of Distances and Angles

Central projection distorts metric properties (e.g.,

lengths, angles) of geometric shapes.

 Points at Infinity

In projective geometry, central projection maps

lines parallel to the projection plane to vanishing

points at infinity, thereby extending Euclidean space

into projective space.

 Desargues’ Theorem

If the lines connecting corresponding vertices of

two triangles meet at a single point (perspector), then

the intersections of their corresponding edges lie on a

straight line (perspectrix), and vice versa.

Figure 4: Desargues Theorem (Picture credit: Original).

As illustrated in figure 4, the author considers two

triangles △𝐴𝐵𝐶 and △ 𝐴′𝐵′𝐶′ . If the connecting

lines of corresponding vertices 𝐴𝐴′,𝐵𝐵′,𝐶𝐶′

intersect at a common point 𝑆 (the perspector), the

triangles exhibit point perspective. Conversely, if the

intersections of corresponding edges denoted 𝑅𝑄𝑃 lie

on a straight line (the perspectrix), they exhibit line

perspective. A pair of triangles are perspective if

either condition is satisfied (Coxeter, 2003; Hartley,

2018).

The conditions and conclusions in Desargues'

theorem are mutually inverse and implicative, which

demonstrates the fundamental principle of point-line

duality in projective geometry. This self-dual

characteristic establishes the foundational status of

Desargues' theorem in projective geometry and

extends its practical utility (Ma, 2011).

Desargues' theorem describes the specific

geometric relations satisfied by two triangles under

A Comparative Study on Central Projection and Parallel Projection

207

the condition that central projection preserves

collinearity and cross-ratio while potentially altering

metric properties such as distances and angles. It

reveals profound properties that remain invariant

when observing geometric figures under different

projection centers. These properties are independent

of specific length or angle measurements, relying

solely on the relative positional relationships of the

figures (Xing et al., 2004).

From an algebraic perspective, Desargues'

theorem reflects the preservation of linear

dependence. In homogeneous coordinates, collinear

points correspond to linearly dependent vectors,

while concurrent lines correspond to linearly

dependent linear equations. The validity of

Desargues' theorem stems from that central

projections corresponds to linear transformations in

vector space, which preserve this dependency

structure (Yu et al., 2011; Sturmfels et al., 2020).

 Mathematical Formulation and Transformation

Matrices

In computer graphics, central projection is widely

used to simulate human visual perception or camera

observation of 3D scenes. Its mathematical

formulation can be implemented via matrices

transformation that generally expressed in

homogeneous coordinates to enable perspective

division.

Assume that:

The projection center (camera optical center) is

located at the origin O(0,0,0).

The projection plane is defined as the 𝑧=𝑓 plane

(where 𝑓>0).

A spatial point 𝑃(𝑋,𝑌,𝑍) is projected onto the

imaging plane as 𝑝(𝑥,𝑦).

Based on the similar triangle principle (see figure

5, right), the following relationships are obtained:

















(2)

The solving for the projected coordinates is:

𝑥=

∙



, 𝑦=

∙



(3)

Here, 𝑍 denotes the depth of point 𝑃, which governs

the scaling effect of the projection and serves as the

divisor in perspective normalization.

When 𝑍=0, the projected point lies behind the

projection center, making it geometrically invalid.

When 𝑍=∞, the projected point approaches a

vanishing point. In Euclidean space, infinite distances

cannot be represented with finite coordinates.

To uniformly describe all points while linearizing

nonlinear central projections, homogeneous

coordinates are introduced (Hartley et al., 2004):

The 3D point 𝑃(𝑋,𝑌,𝑍) is represented as

𝑃(𝑋,𝑌,𝑍,1) in homogeneous coordinates.

The 2D point 𝑃(𝑥,𝑦) is represented as 𝑃(𝑥,𝑦,1)

in homogeneous coordinates.

Using matrix algebra, central projection can be

expressed as a linear transformation in homogeneous

coordinates. The projected point in homogeneous

coordinates is:



𝑥′

𝑦′

𝑤′

=

𝑓



𝑋

𝑌

𝑍

=

𝑓

𝑋

𝑓

𝑌



)

To normalize 𝑥′ , 𝑦′ and 𝑤′ , 2D coordinates are

obtained:

𝑥=





∙



, 𝑦=





∙



)

3.2 Fundamental Theorems and

Properties of Central Projection

In contrast to central projection, parallel projection

does not exhibit vanishing points but preserves more

geometric invariants, with its core parallelism and

proportionality preservation. These properties make

parallel projection indispensable in engineering

drafting, mechanical design, and scientific

visualization.

 Parallelism Preservation

Two parallel lines in space are remain parallel in

the projection plane unless they are parallel to the

projection direction. Lines parallel to the projection

direction degenerate to points.

The parallel preservation theorem is one of the

most critical and widely applied properties of parallel

projection. It guarantees the invariance of parallel

relationships in projective transformations, providing

the theoretical foundation for operations such as

dimension annotation and view correspondence in

engineering drawings. For instance, parallel edges of

mechanical parts remain parallel in orthographic

projections (Shah, 2020).

 Proportionality Preservation

Parallel projection preserves the proportional

lengths of line segments.

The proportionality preservation theorem, rooted

in the linearity of affine transformations, guarantees

the accurate transfer of geometric relationships. This

principle is extensively applied in engineering design,

architectural drafting, and computer graphics.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

208

Orthographic projection preserves angles on the

projection plane, whereas oblique projection

maintains angles only along specific directions (e.g.,

axial directions), with potential distortion in other

orientations.

 Linearity Theorem

Parallel projection is a linear transformation

expressible as an affine transformation matrix. Its

transformation matrix combines a linear matrix and a

translation matrix, classified as an affine

transformation. This affine structure underpins the

validity of the parallelism preservation theorem.

 Mathematical Formulation and

Transformation Matrices

Orthographic projection is the simplest form of

parallel projection, where the mathematical

expression of its transformation matrix for front-view

projection directly discards the 𝑍 coordinate.

Let the object point be 𝑃(𝑋,𝑌,𝑍), projected onto

the plane 𝑧=0 with projection point 𝑝(𝑥,𝑦). The

orthographic projection transformation is given by:



100

010

000



𝑋

𝑌

𝑍

=

𝑥

𝑦

 (6)

Oblique projection may introduce shear distortion

while maintaining parallelism, and can be achieved

by superimposing orthographic projection with shear

transformation (Foley et al., 2018; Shirley et al.,

2016). Let the shear parameters be -a and -b, then the

oblique projection is expressed as:



10−𝑎

01−𝑏

000



𝑋

𝑌

𝑍

=

𝑥

𝑦

 ，



𝑎=𝑐𝑜𝑡𝜃

𝑥

𝑏=𝑐𝑜𝑡𝜃

𝑦

(7)

where 𝜃



( 𝜃



) denote the angle between the

projection direction and the 𝑥 ( 𝑦) axes.

For cabinet Projection, 𝜃=45

，𝑎=𝑏=1.

For cavalier Projection, 𝜃=63.4

，𝑎=𝑏≈

0.5.

Thus, the parameter 𝑐𝑜𝑡𝜃 governs the degree of

distortion in oblique projections.

3.3 Comparative Analysis of Central

and Parallel Projections

Based on the comprehensive analysis of the

definitions, principles, mathematical theorems, and

properties of both central and parallel projections, it

can be found that these two projection methods

exhibit both fundamental differences and intrinsic

connections. The detailed comparative analysis is

enumerated as follows.

From a definitional perspective: Central

projection features a finite distance between the

projection center and the projection plane, with non-

parallel projection lines converging at a single point,

and possesses vanishing points. Parallel projection is

characterized by an infinite projection distance

between the center and plane, resulting in mutually

parallel projection lines with no vanishing points.

From a mathematical perspective: Central

projection is a nonlinear transformation in Euclidean

coordinate systems but can be linearized through the

introduction of homogeneous coordinates, allowing

for matrix-based expression. Parallel projection is

inherently a linear transformation, and its

computation is relatively simple. Whereas central

projections require perspective division and

normalization, which make its computation becoming

complex.

From a geometric perspective: For collinearity

preservation, both central (perspective) and parallel

projections maintain collinearity. For parallelism

preservation, parallel lines of central projection may

converge at vanishing points, but parallel lines of

parallel projection remain strictly parallel. For length

proportionality, central projection exhibits

perspective foreshortening with nonlinear scaling in

distance, while cross-ratios remain preserved. In

contrast, orthographic parallel projection maintains

true length for segments parallel to the projection

plane, and oblique parallel projection allows

adjustable scaling along axial directions. For angular

preservation, central projection causes angular

distortion. Whereas orthographic parallel projection

preserves all angles, and oblique parallel projection

only maintains axial angles, with potential distortion

in other orientations.

Desargues’ theorem and projection applications:

Desargues’ theorem extends the Euclidean plane to

the projective plane by introducing the concepts of

points at infinity and the line at infinity, embodying

the inclusivity and inherent unification of projective

geometry.

Owing to these distinct properties, the two

projection methods exhibit different application

performances. Central projection is typically

employed in scenarios requiring visual effects or

artistic expression, whereas parallel projection is

primarily utilized in precision-dependent applications

such as engineering drawings. Currently, the

integration technique of both projection methods

which combines geometric accuracy and visual

realism has been developed and applied in multiple

domains including computer graphics, architectural

visualization, medical imaging, augmented reality, as

A Comparative Study on Central Projection and Parallel Projection

209

well as cartography and geographic information

systems. Multidimensional representation is achieved

by this hybrid approach of applying parallel

projection to some objects while using perspective

projection for others within the same scene.

4 CASE STUDIES OF CENTRAL

PROJECTION APPLICATION

Due to space limitations, application case of central

projection is exclusively analyzed and discussed in

this section.

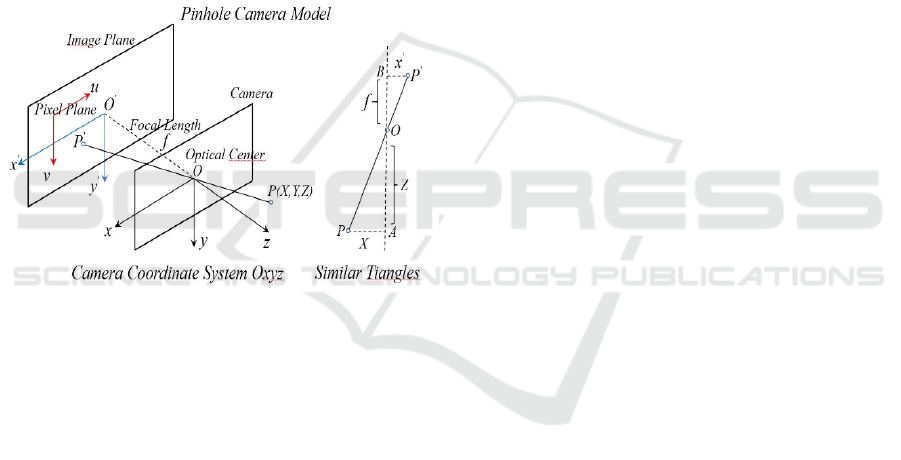
A canonical application of central projection is the

pinhole camera model, whose physical prototype

forms inverted images on the projection plane

through light rays passing via a small aperture, as

illustrated in figure 5.

Figure 5: Pinhole Camera Model (Szeliski, 2022).

The process of digital camera image capture is

fundamentally an optical imaging procedure, with the

pinhole imaging model being the most widely

adopted for camera imaging. This model involves

four coordinate systems: the world coordinate system,

camera coordinate system, image coordinate system,

and pixel coordinate system, along with their mutual

transformations (Hartley et al., 2004; Szeliski, 2022).

The world coordinate system (𝑋,𝑌,𝑍 ), also

referred to as the global coordinate system, defines

the camera's position in 3D space, while the camera

coordinate system originates at the optical center O

with axes x, y, and z. The image coordinate system is

established on the imaging plane 𝑂′𝑥′𝑦′ with

coordinates (𝑥′,𝑦′,𝑧), and the pixel coordinate

system, essentially a matrix-based system, has its

origin at the top-left corner of the image with axes 𝑢

and 𝑣 parallel to 𝑥′ and 𝑦′, where (𝑢,𝑣 )represents

the pixel's row and column indices in the matrix.

Here, 𝑃(𝑋,𝑌,𝑍 ) denotes a point in the world

coordinate system, and 𝑃′ represents its

corresponding projected image point.

The transformation of spatial points from the

world coordinate system to the camera coordinate

system belongs to a rigid-body transformation,

involving solely translation T and rotation R. The

rotation matrix R between the two coordinate systems

can be derived from the axial rotation angles of the

three coordinate axes, while the translation T is

determined by the positions of their coordinate

origins.

The transformation from pixel coordinates (𝑢,𝑣 )

to image coordinates(𝑥′,𝑦′) incorporates both

scaling and translation due to their distinct origins and

scale conventions. The translation parameters and

scaling factors can be calculated based on the

positional relationship between the origins of the two

coordinate systems and the physical dimensions of

pixels in the image coordinate system.

After completing the above two transformations,

an additional step is required to achieve the full

transformation from world coordinates to pixel

coordinates: the transformation from camera

coordinates (𝑥,y ) to image coordinates (𝑥′,𝑦′). This

conversion corresponds precisely to the central

projection transformation, as illustrated in figure 5

(right panel).

Based on the principle of similar triangles, the

transformation relationship can be derived, that is

formula (3) and (5) along with transformation (4) in

Section 3.1.

In the process of the complete transformation,

𝑅 and 𝑇constitute the extrinsic parameters of the

camera, defining its pose in the world coordinate

system. The intrinsic parameters, encapsulated in the

calibration matrix 𝐾 , are derived from the focal

length 𝑓 and the transformation coefficients between

image and pixel coordinates. Both intrinsic and

extrinsic parameters can be estimated through

established calibration procedures (Zhang, 2000).

Algorithm is implemented and executed

according to the above steps:

The extrinsic parameters of the rotation matrix 𝑅

and translation vector 𝑇

for the world-to-camera

coordinate transformation are computed first.

Subsequently, the intrinsic parameter calibration of

the projection matrix 𝐾 encapsulating focal length

𝑓 and image-to-pixel coordinate conversions is

estimated. Finally, perspective normalization is

performed through perspective division to obtain

normalized coordinates.

The practical implementation can be achieved

through programming in various computer languages.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

210

In this paper, MATLAB programming is adopted, but

the source code is not provided here due to space

constraints.

5 CONCLUSION

In summary, as two fundamental projection methods

in projection theory, parallel projection and central

projection differ in their definitions, underlying

principles, mathematical formulations, exhibited

properties, and application domains.

Mathematically, central projection is based on

perspective geometry, where all projection lines

converge at the viewpoint, forming a conical

projection structure. The most distinctive feature that

distinguishes it from parallel projection is the

convergence of parallel lines at vanishing points on

the projection plane. This results in an inverse

relationship between object size and the distance from

the object point to the projection center (viewpoint),

producing the characteristic 'foreshortening' visual

effect. By contrast, parallelism in space is preserved

in parallel projection, whether orthographic or

oblique, with all projection lines remaining parallel,

where projected dimensions are independent from the

distance (the depth compression ratio of cabinet

oblique projection is 0.5). It is this fundamental

dichotomy dictates that dictates their divergent

applications.

Visually, central projection aligns with human

visual perception by generating spatial depth cues,

making it suitable for applications requiring realism,

such as creating cinematic visual effects and

discerning accurate architectural spatial relationships

in through strategically placed vanishing points. In

contrast, although parallel projection lacks depth

perception, its ability to preserve geometric invariants

makes it indispensable for technical drawings.

Orthographic multi-view projections provide

dimensional accuracy for mechanical component

designs, while axonometric projections in

architectural drafting offer three-dimensional

visualization without perspective distortion.

With the development of science and technology,

projection technology has also been evolving and

innovating. The integration technology combining

these two projection methods is being applied in a

growing number of fields. It is believed that both

projection approaches will further develop toward

greater intelligence, automation, and cross-domain

integration, enabling broader applications in the

future.

REFERENCES

Carlson, W. E., 2003. A Critical History of Computer

Graphics and Animation (Online textbook). Ohio State

University, 87-92.

Chen, L., Zhang, W. W., Li, H., Xu, J., 2018. Plane-Based

Calibration for Structured Light Systems Using Cross-

Ratio Constraint. Optics and Lasers in Engineering,

110, 1-8.

Cipolla, R., Drummond, T., Robertson, D. P., Blake, A.,

1999. Camera Calibration from Vanishing Points in

Images of Architectural Scenes. IEEE CVPR, 2, 382-

387.

Coxeter, H. S. M., 2003. Projective Geometry. Springer,

Berlin, 2

Edition, 23-61.

Foley, J. D., Van Dam, A., Feiner, S. K., Hughes, J. F.,

2018. Computer Graphics: Principles and Practice.

China Machine Press. Beijing, 3

Edition, 272-275.

Garcia, E. S., He, M. M., Mueller, k.,2019. Artistic Style

Transfer with Controlled Perspective Distortion.

Journal of Computer Graphics Techniques,18(3), 72-

89.

Hartley, R., Zisserman, A., 2004. Multiple View Geometry

in Computer Vision. Cambridge University Press,

Cambridge, 2

Edition, 155-160+225-228.

Liu, H. W., 2022. Application of Projection Technology in

Computer-Aided Design and Programming for Stone

Product Processing. Stone, 3, 26-31+39.

Liu, Y., d., Lü, Y. W., Du, B. J., Gong, X. R., Huang, X.,

2024. Projection Center and Triple Difference

Detection Method of T-Type Photoelectric Theodolite.

Acta Optica Sinica, 44(2),1-10.

Luo, W., Deng, X. W., 2009, The teaching discussion on

the building direction in civil engineering major. Shanxi

Architecture, 35 (11), 194-196.

Ma, Y., F., 2011. Popularization on Application of

Desargues Theorem and its Inverse. Journal of Gansu

Lianhe University (Natural Sciences), 25(2), 95-97.

Müller, S., Zhang, Y., 2011. Comparative Analysis of

Orthographic vs Perspective Projection in CAD-Based

Industrial Design. Computer-Aided Design, 130, 45-58.

Peacock, K., Druckrey, T., 2001. Projective

Transformations in Digital Art. Leonardo, 34(3), 203-

208.

Shah, J. J., 2020. Parametric and Feature-Based

CAD/CAM: Concepts, Techniques, and Applications.

ASME Press, New York, 2

Edition, 189-201.

Shirley, P., Marschner, S., Ashikhmin ， M., 2016.

Fundamentals of Computer Graphics. AK Peters/CRC

Press, Boca Raton, 4

Edition, 135-153.

Sturmfels, B., Pajdla, T., Kileel, J., 2020. Algebraic

Geometry of Computer Vision. Foundations of

Computational Mathematics, 20(5), 1123-1150.

Szeliski, R., 2022. Computer Vision: Algorithms and

Applications. Springer, Berlin, 2

Edition, 52-55.

Xing, Y. F., Hu, Z. Y., Zhang, J., 2004. Projective

Invariants for Vision-Based Measurement. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 26(11), 1454-1460.

A Comparative Study on Central Projection and Parallel Projection

211

Yu, J. B., Ponce, J., Hebert, M., 2011. Algebraic

Foundations of Projective Geometry in Computer

Vision. Journal of Mathematical Imaging and Vision,

39(2), 120-135.

Zhang, S. X., Ye, H., 2008. Projection and Painting Art.

Journal of Engineering Graphics, 2008(5), 107-110.

Zhang, Y., Chen, X. D., Wang, L., 2015. Shadow-Based

Geometric Calibration of Sun Sensors Using Cross-

Ratio Invariance. IEEE Transactions on

Instrumentation and Measurement, 64(6), 1520-1531.

Zhang, Z. Y., 2000. A Flexible New Technique for Camera

Calibration. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 22(11), 1330-1334.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

212