
Analysis of the Principle and the State-of-Art Results for Searching
Gravitational Waves
Kenuo Qiao
a
School of Physical Science and Engineering, Tongji University, Shanghai, China
Keywords: General Relativity, Gravitational Waves, Laser Interferometry, Binary Neutron Star Merger.
Abstract: As a direct mathematical derivation of Einstein's general theory of relativity, the detection of gravitational
waves is direct evidence of the correctness of Einstein's theory of gravity and provides a new perspective for
studying the universe. This study focuses on the basic mathematical derivation, detection principles, and latest
research achievements of gravitational waves, especially the application of laser interferometry. Through laser
interferometry, detectors (e.g., LIGO and Virgo) have successfully detected multiple gravitational wave
events, such as the binary neutron star merger event GW170817, verifying the predictions of general relativity
and predicting various properties of neutron stars. Gravitational wave detection provides a key tool for
studying galaxy evolution, black hole growth mechanisms, and the origin of the universe. At the end of this
study, prospects are given for the new generation of detectors and space exploration programs, which will
further enhance the sensitivity of gravitational wave detection and reveal more mysteries of the universe.
1 INTRODUCTION
Albert Einstein’s general relativity, established in
1915, provided a new research perspective for
physics and astronomy, by which there are many
astronomical observation phenomena can be
explained. For example, the Mercury precession rate
was observed as 133'20'' per century and eventually
proved by general relativity, where an ineligible error
was aroused by Newton’s gravitational theory
(Yahalom, 2023). Although there are many indirect
proofs standing for the correctness of General
Relativity, theoretical physicists tend to find the
direct proof (Cervantes-Cota, et al., 2016). That is the
initial motivation for detecting gravitational waves
(GW), as it is direct mathematical deduction from
Einstein’s theory of gravity.
Since GW manifests the perturbation of
spacetime, they change the length of objects though
the change is extremely unobvious due to the
weakness of relativistic effect. In 1960, Joseph Weber
described his ideas of detecting the micro change of
the length of a cylinder made of aluminium caused by
GW (Cervantes-Cota, et al., 2016; Yu, et al., 2019).
However, the experiment ended up with no results. It
was not for the crude experimental environment (on
a
https://orcid.org/0009-0000-2533-171X
the contrary, the environment he set up eliminated a
lot of noise, thunderstorms, cosmic rays showers,
power supply fluctuations, etc. (Cervantes-Cota, et
al., 2016; Yu, et al., 2019)), but for the failure of basic
principles. Because there was still a kind of noise
caused by thermal agitation (Cervantes-Cota, et al.,
2016; Yu, et al., 2019) that cannot be removed and
the gravitational signal he wanted was not much
greater than this noise.
Then, in 1974, Joseph Hooten Taylor and Alan
Russell Hulse found that the rotating radius of binary
pulsars was decreasing (Yu, et al., 2019). This
discovery can be explained as the radiation of GW
leading to such decreasing. It was a new proof of the
existence of GW. The progress also gave physicists
hope to continue detecting the gravitational signals.
Finally, exactly 100 years after the theory of general
relativity and the prediction of GW were born, on 14
September 2015, these wave signals were pronounced
to be detected by researchers in LIGO (the
abbreviation from Laser Interferometer GW
Observatory) and have been confirmed to be indeed
GW (Yu, et al., 2019).
Besides LIGO, more and more other detectors
were developed such as Virgo, located in Europe, also
based on the principle of laser interferometer (Barish,
172
Qiao, K.
Analysis of the Principle and the State-of-Art Results for Searching Gravitational Waves.
DOI: 10.5220/0013821600004708
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 172-179
ISBN: 978-989-758-774-0
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

& Weiss, 1999). With the coordinative operation
between LIGO and Virgo, the localization area of
GW sources has been reduced from a large range
when using LIGO alone to a relatively small sky
region, which is crucial for subsequent follow-up
observations in the electromagnetic band using other
astronomical equipment such as optical telescopes,
radio telescopes, etc. For example, GW170817, found
in 2017, is a united detecting campaign across many
fields, which will be introduced in Sec 4.
In recent years, with the development of space
technology, people plan to build GW detectors on a
larger scale in space, known as Space GW Detection
Program (Ni, 2024). These are cutting-edge concepts
for GW detection. For example, LISA, a space GW
detection program jointly launched by the European
Space Agency (ESA) and the National Aeronautics
and Space Administration of the United States
(NASA), consisted with an equilateral triangular
array composed of three identical spacecraft, located
approximately 2.5 million kilometres apart from each
other. This greatly increases the spatial scale changes
caused by GW, making it easier to detect changes in
laser interference fringes. Besides, China's Taiji
program (Ni, 2024) also aims to build a GW detection
platform in space, using satellite formations to
capture GW signals by measuring changes in distance
between satellites through laser interferometry. The
detection of GW is of great significance for studying
the evolution of galaxies, the growth mechanism of
black holes, and revealing the origin and early
evolution process of the universe.
This research aims to summarize the historical
background of theoretical predictions and detection
of GW, introduce the basic theoretical formulas of
GW and the basic principles and details of some
detection methods, as well as their shortcomings. On
this basis, this study will discuss some research
limitations of GW and some prospects for future
research, intending to provide a comprehensive
summary and introduction to the study of GW, to
encourage inspiration for future research.
2 DESCRIPTIONS OF GW
GW are classified into three types: stochastic,
periodic and impulsive (Cervantes-Cota, et al., 2016).
Most stochastic waves origin from the very early era
of the universe or even in the Big Bang, which acts
randomly and are difficult to detect. Because of their
irregular fluctuation, it is hard to separate them from
the background noises of our instruments and then
identify them. For periodic waves, they refer to the
kind of waves that own relatively stable and constant
frequency. These waves may generate from binary
neutron star (BNS) systems where the two stars rotate
with each other (accurately, around the centre of
mass). The third type of wave, impulsive, can be
analogous to a burst of a signal. These waves
correspond to and origin from some instant events,
like binary black hole (BBH) merger, the explosion
of supernovas or the creation of new black holes. GW
are basically the radiation of the energy converted
from lost mass of celestial bodies (Cervantes-Cota, et
al., 2016).
The following part narrates a short derivation and
deduction of the wave functions beginning with
Einstein’s field equations. Einstein’s theory of
general relativity is approximated to Newton’s theory
of gravity when the gravitational field is weak and
static, and the particles move much more slowly than
the speed of light (Chakrabarty, 1999). One now
considers it as a perturbation on the flat Minkowski
metric:
𝑔
=𝜂
+ℎ
, ℎ
≪1
(
1
)
Indices of any tensor can be raised or lowered using
𝜂
or 𝜂
respectively because of the weakness of
the perturbation. Therefore,
𝑔
=𝜂
−ℎ
(
2
)
The perturbation transforms under Lorentz
transformation as a second-rank tensor:
ℎ
=Λ
Λ
ℎ
(
3
)
By continuously calculating the affine connection and
the Riemann curvature tensor, one obtains Ricci
scalar as
𝑅=𝜕
𝜕
ℎ
−□ℎ
(
4
)
The Einstein tensor, 𝐺
, in weak field is
𝐺
=𝑅
−
1
2
𝜂
𝑅=
1
2
(𝜕
𝜕
ℎ
+𝜕
𝜕
ℎ
−
𝜂
𝜕
𝜕
ℎ
+𝜂
□ℎ − □ℎ
)
(
5
)
The linearized Einstein field equations are then
𝐺
=8𝜋𝐺𝑇
(
6
)
or its equivalent form:
□
ℎ
−𝜕
𝜕
ℎ
−𝜕
𝜕
ℎ
+𝜕
𝜕
ℎ=
−16𝜋𝐺𝑆
(
7
)
where
𝑆
≡𝑇
−
1
2
𝜂
𝑇
(
8
)
The equations have infinitely many solutions because
one can always transform the form of one solution to
another form by changing the coordinate system.
However, one can utilize a specific gauge
transformation and work under a selected coordinate
system. One such coordinate system is the harmonic
coordinate system. The gauge condition is
Analysis of the Principle and the State-of-Art Results for Searching Gravitational Waves
173

𝑔
Γ
=0
(
9
)
In the weak field limit, this condition reduces to
𝜕
ℎ
=
1
2
𝜕
ℎ
(
10
)
Utilizing it to simplify the linearized Einstein field
equations, one obtains
□
ℎ
=−16𝜋𝐺𝑆
(
11
)
In vacuum,
□
ℎ
=0
(
12
)
It is analogous with the wave function of
electromagnetism, and it obviously has the plane-
wave solutions
ℎ
=𝜖
exp
(
𝑖𝑘
𝑥
)
+𝜖
∗
exp (−𝑖𝑘
𝑥
)
(
13
)
where 𝑘
=𝜔,𝑘
⃗
and 𝜖
is the polarization tensor.
Plugging in the solution Eq. (13) into the Eq. (12), one
obtains
𝑘
𝑘
=0
(
14
)
which means 𝑘
=0 and GW propagates at the speed
of light. Using the harmonic gauge condition, one
finds 𝜖
is orthogonal to 𝑘
:
𝑘
𝜖
=
1
2
𝑘
𝜖
(
15
)
Therefore, GW is transverse. There are ten
independent components in a symmetric rank-2
tensor, so that its degrees of freedom are also ten. One
can utilize four equations from Eq. (15) to reduce the
degrees of freedom of 𝜖
to six. However, under
such gauge conditions there are still many coordinate
selections. By finalizing the coordinate system used,
another four equations can be obtained, which again
reduces the number of independent components of
𝜖
to 2. Considering a minor coordinate
transformation:
𝑥
=𝑥
+𝜉
(
16
)
and the metric tensor transforms as:
𝑔
=
𝜕𝑥
𝜕𝑥
𝜕𝑥
𝜕𝑥
𝑔
(
17
)
reserving it to the first order:
ℎ
=ℎ
−𝜕
𝜉
−𝜕
𝜉
(
18
)
and the form of 𝜉
one used is
𝜉
=𝑖𝑒
exp
(
𝑖𝑘
𝑥
)
−𝑖𝑒
∗
exp
(
−𝑖𝑘
𝑥
)(
19
)
Plugging in it into the Eq. (18), one obtains
𝜖
=𝜖
+𝑘
𝑒
+𝑘
𝑒
(
20
)
Now, one has determined the specific coordinate
system with 𝑒
. It is obvious that there are four more
additional conditions, and the final degrees of
freedom are 2, which are also the only two physical
degrees of freedom. One considers the wave
propagates along z-axis, so there are four non-zero
components in 𝜖
:
𝜖
=−𝜖
,𝜖
=𝜖
(
21
)
The trace of 𝜖
is obviously zero. Considering the
wave is transverse, one names the gauge conditions
as transverse traceless (TT) (Flanagan & Hughes,
2005). The matrix form is
𝜖
=
00 00
0𝜖
𝜖
0
0𝜖
−𝜖
0
00 00
(
22
)
Now, one is going to find the solutions of the Eq. (11).
Using the Green’s function, one obtains
ℎ
(
𝑥⃗,𝑡
)
=4𝐺𝑑
𝑥⃗′
𝑆
(
𝑥⃗
,𝑡−
|
𝑥⃗−𝑥⃗
|)
|
𝑥⃗−𝑥⃗
|
(
23
)
where one uses the natural unit system, and this
indicates that the perturbation of the spacetime
radiates from the material distribution from the
distance of
|
𝑥⃗−𝑥⃗
|
. And the greater the mass, the
more intense the radiation (Cervantes-Cota, et al.,
2016).
3 PRINCIPLE AND FACILITIES
The Eq. (23) give some inspiration for the detection
of GW. To measure the change of scales of objects,
one defines the gravitational-wave amplitude ℎ as
(Pitkin, et al., 2011):
ℎ=
2Δ𝐿
𝐿
(
24
)
which is basically the proportion between the change
of length and the initial length and one can consider
it as perturbation ℎ
discussed in Sec 2. As a matter
of fact, different astrophysical events radiate waves in
different frequencies and with different amplitudes.
Most of the amplitudes are very small, only 10
or
even smaller, depending on specific sources (Pitkin,
et al., 2011). Therefore, removing various noises is
the main technical key point and difficulty for the
detection.
Laser interferometry provides the possibility of
very high sensitivity over a wide frequency range. It
drew inspiration from the design of the Michelson
interferometer, which consists of two mirrors and a
half mirror (seen from Fig. 1 (Pitkin, et al., 2011)).
When the laser travels along the optical path, it is
divided into two beams and eventually reassembles to
interfere and produce interference fringes. When GW
interact with the instrument, the distance between the
mirrors is changed, that is, the optical path is changed,
so the interference fringes will move. One can use
computers to detect GW by converting optical signals
into electrical signals. That is the basic principle of
laser interferometry.
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
174
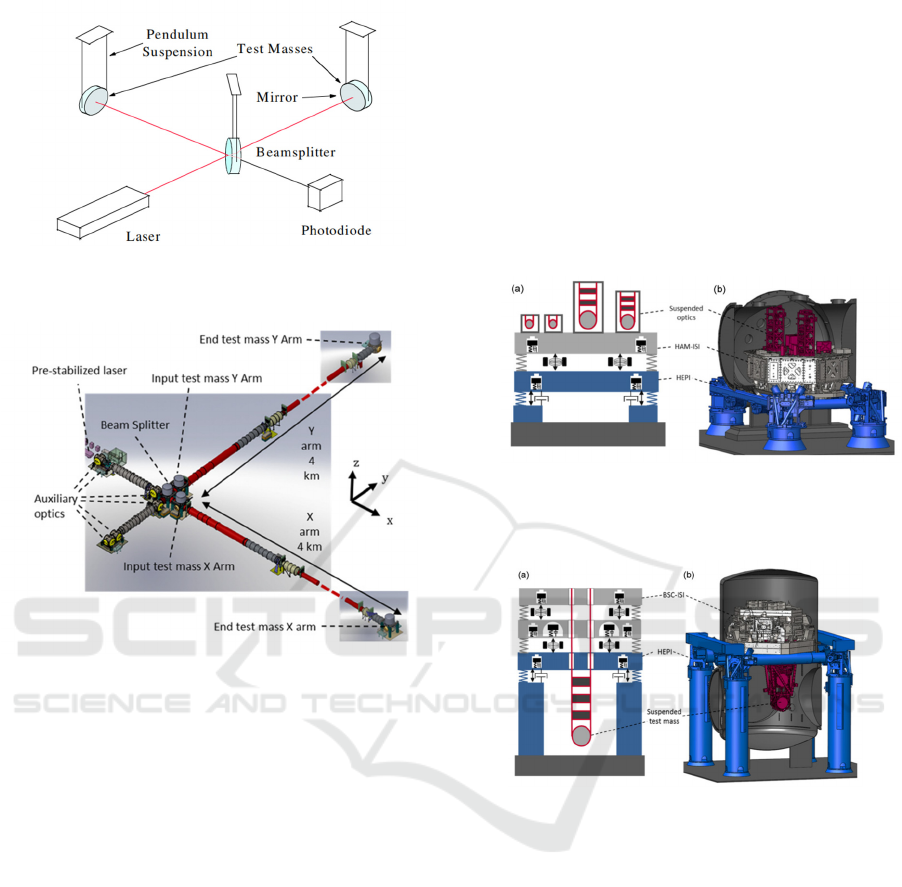
Figure 1: Structure of gravitational-wave detector based on
laser interferometry (Pitkin, et al., 2011).
Figure 2: Representation of the LIGO vacuum system
(Matichard, et al., 2015).
As the first detector to detect GW signals, LIGO
project includes two identical detection devices,
located in Hanford (WA) and Livingston (LA). Fig. 2
shows the vacuum enclosure and instrument
equipment (Matichard, et al., 2015). Each detector
uses 11 vacuum tanks (Matichard, et al., 2015). Five
of them are large balanced scorecard chambers (with
a diameter of approximately 4.5 meters and 2.5
meters), which contain the core optical system of the
interferometer (Matichard, et al., 2015). Six of them
are smaller HAM chambers (approximately 2.5
meters high and 2.5 meters wide) that house auxiliary
optical equipment for interferometers (Matichard, et
al., 2015).
The auxiliary optical system in LIGO is also a
major highlight, as the initial laser beam emitted by
the laser source may have an uneven intensity
distribution or a shape that does not meet the
requirements of the interferometer (Matichard, et al.,
2015). The beam shaping element in the auxiliary
optical system is used to shape the laser beam into a
specific shape, such as a Gaussian beam shape.
Gaussian beams have the characteristic of high
central intensity and gradually decreasing edge
intensity, which is beneficial for propagation in
interferometers and reduces aberrations and other
issues. By using specially designed optical
components such as lens groups or non-spherical
mirrors, the intensity distribution of the laser beam
can be precisely controlled to ensure that the laser
beam has a suitable intensity distribution in various
parts of the interferometer, thereby improving the
accuracy of interferometric measurements. Some
sophisticated structures are shown in Fig. 3 and Fig.
4 (Matichard, et al., 2015).
Figure 3: (a) Schematic and (b) CAD model of the isolation
systems supporting the auxiliary optics in the HAM
chambers (Matichard, et al., 2015).
Figure 4: (a) Schematic and (b) CAD model of the isolation
systems supporting the core optics in the BSC chambers
(Matichard, et al., 2015).
Pulsars are high-speed rotating neutron stars that
emit very regular pulse signals. When GWs propagate
in the universe, they stretch and compress spacetime,
thereby affecting the time interval for pulsar signals
to reach Earth. By observing the changes in the arrival
time of signals from multiple pulsars and constructing
a pulsar timing array, the presence of GW can be
detected. If GW pass through the spacetime between
Earth and a pulsar, it will cause small regular changes
in the arrival time of the pulsar signal on Earth, which
can be observed by high-precision radio telescopes
(Johnson, et al., 2024). The advantage of pulsar
timing array is its high detection sensitivity to low-
frequency GW (Johnson, et al., 2024). Unlike laser
interferometric GW detectors such as LIGO and
Virgo, which mainly target high-frequency GW,
Analysis of the Principle and the State-of-Art Results for Searching Gravitational Waves
175
pulsar timing arrays can detect GW in the nanohertz
frequency range, which corresponds to some
important massive astrophysical processes in the
universe, e.g., the merger of supermassive black holes,
the formation and evolution of galaxies.
There are many observatories primarily used for
observing pulsars to detect GW in the world. For
example, the Parkes Radio Telescope Observatory in
Australia, the Effelsberg Radio Observatory in
Europe, and the Green Bank Observatory in the
United States (Johnson, et al., 2024). They have all
obtained a large amount of pulsar data, which can be
filtered to obtain information about GW. There
actually has been some data obtained through the
observation by such method, but the analysis of them
is still at the fundamental level and it still cannot be
sure that if such method is a stable technology and can
be generalized to detect GW.
4 OBSERVATION RESULTS AND
ANALYSIS
Subsequently, one focuses on the discussion about
GW from binary stellar objects like BNS and BBH.
One first gives some dynamic and post-Newtonian
explanation about the principle of binary system
emitting GW and then analyse some data about BNS
obtained in recent year.
A binary object system that is constrained by
gravity rotates around the centre of mass. In classical
Newtonian theory, it is a conservative system and
keeps a conservation of energy, that the orbits remain
quasi-spherical and will not shrink. However, in post-
Newtonian theory, factor 𝑣
/𝑐
should be considered
(where 𝑣 is the velocity of object and 𝑐 is the speed
of light). So, the separation between two bodies
decreases and the rotating frequency rises, due to the
emission of GW causes the decline of orbital angular
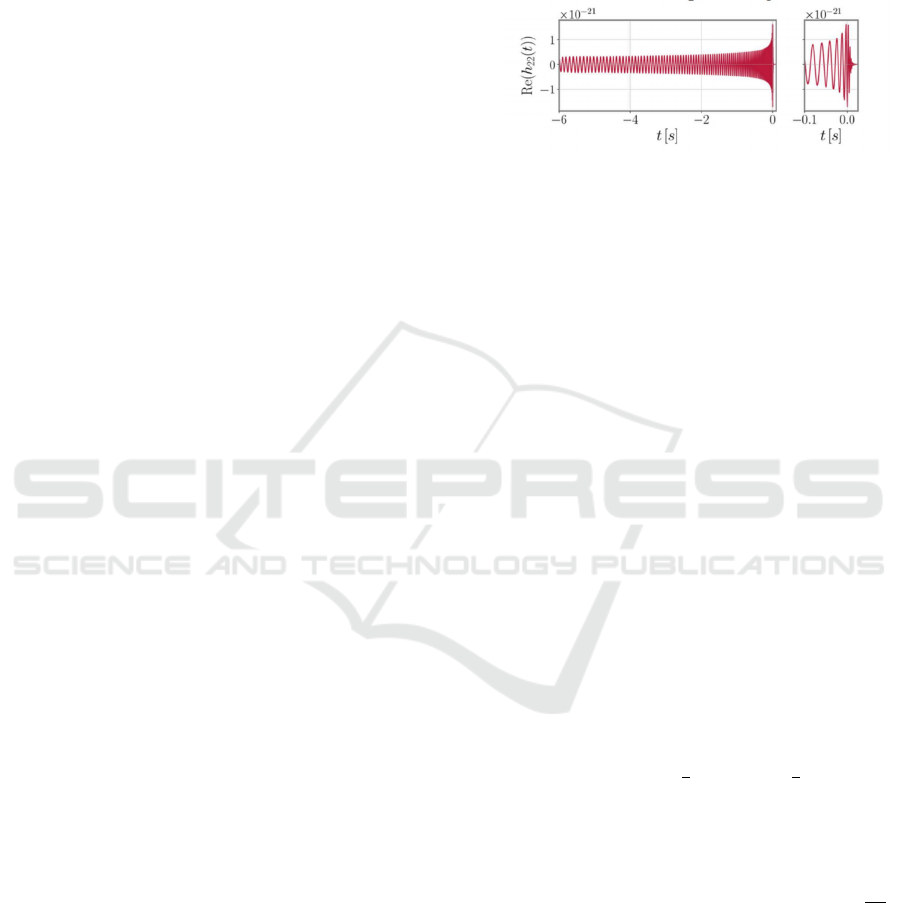
momentum. The phenomenon of GW rising
frequency is called chirping and the waveform is
shown as in Fig. 5 (Schmidt, 2021). The orbit is
regarded as a plane and the orientation of orbital
angular momentum is stable, despite the orbital
precession result from any angular perturbation. The
negligibility of precession leads to the approximately
fixed direction of GW propagation, and the wave can
be measured with the component ℎ
. The whole
process of binary system evolution falls roughly into
three periods: inspiral, merger and ringdown. Figure
5 (right) shows the waveform of late inspiral-period
and the merger-period. Through interferometric
principle on which detectors based, time-frequency
and time-amplitude data representations can be
collected to analyze the properties of GW and further
the properties of source by using theoretical results of
post-Newtonian theory or, using general relativity for
ineligible case when objects are about to merge and
the velocities are close to speed of light.
Figure 5: The GW form of a non-spinning 30+ 30𝑀
binary black hole at a distance of 400Mpc (Schmidt, 2021).
For recent data about BNS, asSSS17a/AT 2017gfo
was the united campaign organized to precisely
observe and analyze captured GW after people in
Advanced LIGO realized the GW signal was being
received in August 2017. It was the first time for
humanity to conduct the united detection across
domains of astrophysics, GW and electromagnetism.
The signal detected was the strongest GW signal up
to that time, with a combined signal-to-noise ratio
(SNR) of 32.4 (Abbott, et al., 2017; Abbott, et al.,
2019), lasting about 100s (Abbott, et al., 2017), as
shown in Fig. 6 (Abbott, et al., 2017). The
observation was a joint campaign involving the data
derived by two instruments from LIGO (Hanford and
Livingston) and the detector from Virgo. From
Einstein’s general relativity one obtains that as binary
system rotating, the rotating frequency, i.e., the
frequency of GW emitted from the system, will rise
corresponding to the shrink of orbit, which was
consistent with discussed earlier. The increasing
frequency closely related to a form of combination
with stellar masses, which is called the chirp mass (𝑀)
(Abbott, et al., 2019), and one has
𝑀=
(
𝑚
𝑚
)
(
𝑚
+𝑚
)
(
25
)
By analysing the frequencies data from figure 5
collected by the three interferometers, researchers
found that the chirp mass of the wave source well
matched that of the binary neutron star (BNS) system.
Moreover, combining with the mass rate 𝑞=
,
where 𝑚
𝑚
, it was verified that this GW was
most probably from the process of a BNS merger
(despite the possibility of other stellar binary systems
(Abbott, et al., 2017) since not much strict and
cramped interval of mass, electromagnetic and
astrophysical observation afterwards both proved the
source was BNS).
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
176
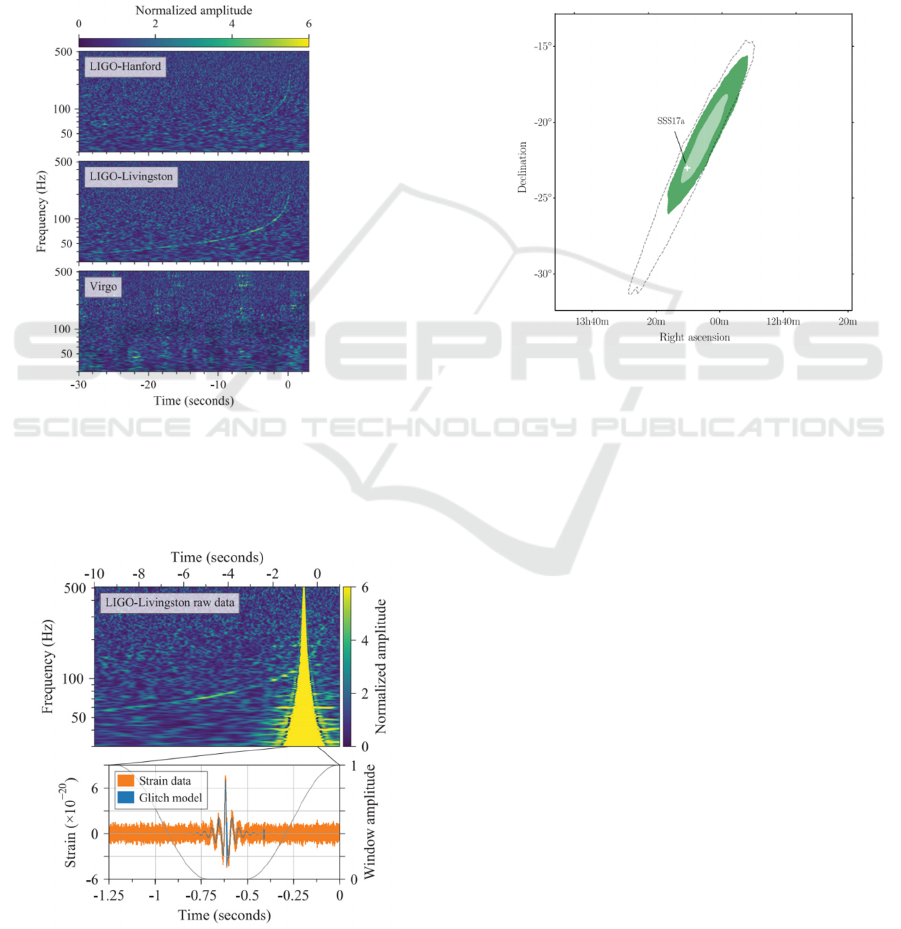
During the detection, there was one noise, or
glitch, caused by instrumental error of LIGO-
Livingston, should be subtracted from the data. The
window function (Abbott, et al., 2017) was used to
make the effect of the glitch to be the minimum, as
the sine-like-shaped brown curve illustrated in Fig. 7
(Abbott, et al., 2017), which was based on sine
function mode and mitigated the value from
unexpected coordinate band. After that, a rapid
binary-coalescence reanalysis (Abbott, et al., 2017)
was used to localize the source of BNS with correct
data.
Figure 6: Time-frequency representations of data
containing the gravitational-wave event GW170817,
observed by the LIGO-Hanford (top), LIGO-Livingston
(middle), and Virgo (bottom) detectors (Abbott, et al.,
2017).
Figure 7: Mitigation of the glitch in LIGO-Livingston data
(Abbott, et al., 2017).
Additionally, a 𝛾-ray burst occurred following the
merger and was identified by electromagnetic
detectors. So, both electromagnetic method and GW
method named rapid binary-coalescence reanalysis
(Abbott, et al., 2017) were utilized to convincingly
localize the source of radiation. Simultaneously,
astrophysical observation was also organized,
attaining consistent result, and finally determined the
location of the BNS source that it was near the galaxy
NGC 4993 (Abbott, et al., 2017; Abbott, et al., 2019).
The detailed location was presented in Fig. 8 (Abbott,
et al., 2019).
Figure 8: The improved localization of GW170817, with
the location of the associated counterpart SSS17a/AT
2017gfo (Abbott, et al., 2019).
5 LIMITATIONS AND
PROSPECTS
The current gravitational wave detection technology
still has many limitations. The current GW detectors
(e.g., LIGO, Virgo, KAGRA) still have limited
sensitivity in detecting GW, especially in detecting
extreme frequency signals. For low-frequency signals
(<10 Hz), ground detectors are difficult to effectively
detect because noise on Earth (Pitkin, et al., 2011;
Matichard, et al., 2015) (e.g., earthquakes, human
activities) can interfere with the signal. For high-
frequency signals (>10 kHz), current detectors have
low resolution for high-frequency signals and may
miss some important physical phenomena.
Meanwhile, GW signals are very weak and easily
masked by environmental noise such as earthquakes,
waves, temperature changes, etc. Although the impact
of noise can be partially reduced through multi
detector networks and data analysis techniques,
eliminating it remains a challenge. In addition, some
Analysis of the Principle and the State-of-Art Results for Searching Gravitational Waves
177
noise, such as quantum noise, cannot be theoretically
eliminated because it exists in the form of quantum
radiation pressure noise based on photon technology
(Abbott, et al., 2017). Among other advances, A+ (the
planned advanced LIGO upgrade) will improve
LIGO’s broadband sensitivity by using the technique
of quantum light squeezing to reduce laser phase
noise at high frequencies and radiation pressure noise
at low frequencies (Coleman Miller, & Yunes, 2022).
In addition, the analysis of gravitational wave
signals relies on theoretical models, such as
numerical relativistic simulations (Schmidt, 2021) of
BBH merger. However, these models may not be
entirely accurate, as described in Sec. 4.1, especially
under extreme conditions such as extremely high
densities, strong gravitational fields, etc. The post
Newtonian model is no longer applicable and requires
the use of numerical relativity theory to perform
numerical calculations and analysis using computers,
which can result in numerical errors.
Based on considerations of current limitations,
there have been developments and prospects in recent
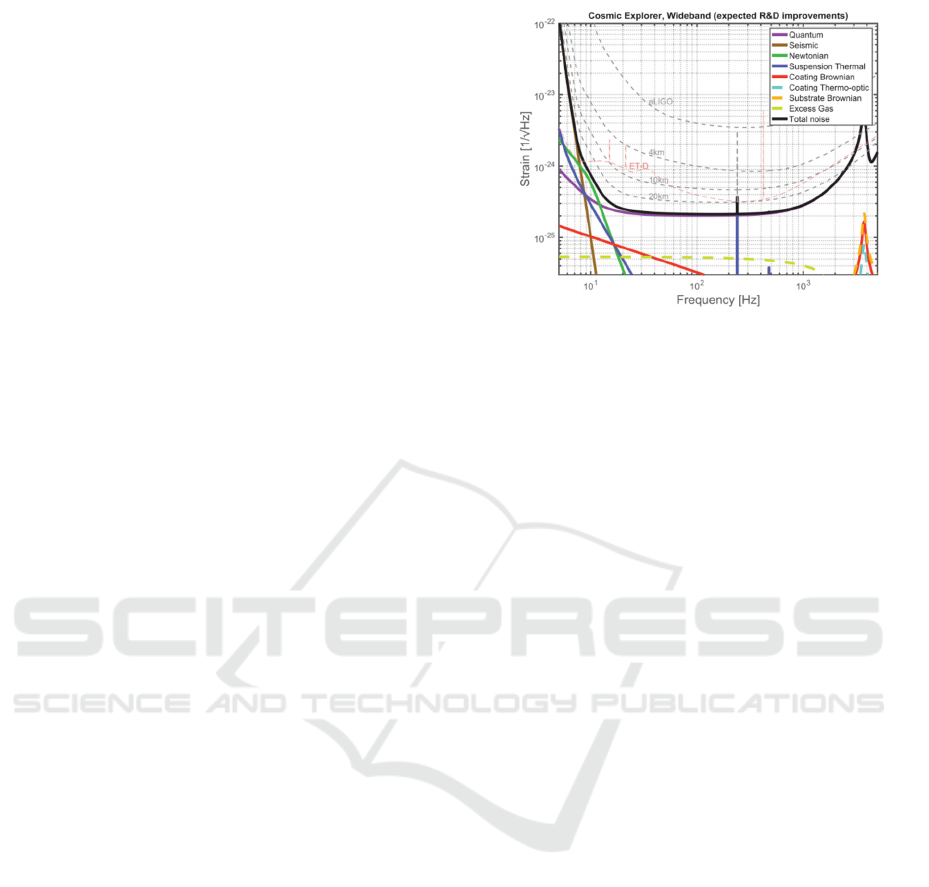
years. For example, the outlook for the construction
of a new generation of detectors is that future ground-
based gravitational wave detectors such as Einstein
Telescope and Cosmic Explorer (Abbott, et al., 2017;
Bailes, et al., 2021) (Sensitivity of expected improved
Cosmic Explorer is shown in Fig. 9 compared with
that of Advanced LIGO and several types of noise)
will have higher sensitivity, be able to detect more
distant and weaker gravitational wave signals, and
cover a wider frequency range (Abbott, et al., 2017).
At the same time, in order to obtain a larger
observation frequency band, space probes are being
planned for construction. Space based gravitational
wave detectors (such as LISA, DECIGO, BBO
(Bailes, et al., 2021)) will be able to detect low-
frequency gravitational waves (in the band of mHz to
Hz) and study celestial physical processes such as
supermassive black hole mergers and galaxy
evolution.
Gravitational waves are also a crucial tool for
studying the evolution of the early universe. The Big
Bang model shows how the universe inflated from an
initial state of extremely high density to the universe
we currently inhabit (Ringwald, & Tamarit, 2022). It
successfully traces the history of the universe back to
a fraction of a second after birth, but direct
information about the history of the universe before
the Big Bang nuclear fusion can be obtained through
observations of gravitational waves (Ringwald, &
Tamarit, 2022). Future space probes may be able to
directly detect these signals, providing us with new
clues about the origin and evolution of the universe.
Figure 9. Target sensitivity for a next generation
gravitational-wave detector (Abbott, et al., 2017).
6 CONCLUSIONS
To sum up, this study summarizes the historical
background, basic theoretical formulas, and detection
methods of gravitational wave detection, analyses the
limitations of current technology, and discusses
future research prospects. By detecting gravitational
waves, scientists can study the evolution of galaxies,
the growth mechanism of black holes, and the origin
and early evolution of the universe. Future space
probes and next-generation ground probes will
further enhance the sensitivity of gravitational wave
detection, enabling us to detect signals that are farther
and weaker, thus revealing more mysteries about the
universe. This study provides a comprehensive
summary and introduction for the in-depth
exploration of the field of gravitational waves,
inspiring inspiration for future research.
REFERENCES
Abbott, B. P., Abbott, R., Abbott, T., et al., 2017.
GW170817: observation of gravitational waves from a
binary neutron star inspiral. Physical Review Letters,
119(16), 161101.
Abbott, B. P., Abbott, R., Abbott, T. D., et al., 2017.
Exploring the sensitivity of next generation
gravitational wave detectors. Classical and Quantum
Gravity, 34(4), 044001.
Abbott, B., Abbott, R., Abbott, T. D., et al., 2019.
Properties of the binary neutron star merger GW170817.
Physical Review X, 9(1), 011001.
Bailes, M., Berger, B. K., Brady, P. R., et al., 2021.
Gravitational-wave physics and astronomy in the 2020s
and 2030s. Nature Reviews Physics, 3, 145-159.
IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy
178

Barish, B. C., Weiss, R., 1999. LIGO and the detection of
gravitational waves. Physics Today, 52(10), 44-50.
Cervantes-Cota, J. L., Galindo-Uribarri, S., Smoot, G. F.,
2016. A brief history of gravitational waves. Reviews in
Physics, 1(3), 16002.
Chakrabarty, I., 1999. Gravitational Waves: An
Introduction, arXiv.physics/9908041
Coleman Miller, M., Yunes, N., 2022. The new frontier of
gravitational waves. Reviews of Modern Physics, 94(4),
045002.
Flanagan, E., Hughes, S. A., 2005. The basics of
gravitational wave theory. New Journal of Physics, 7,
204.
Johnson, A. D., Meyers, P. M., Baker, P. T., et al., 2024.
NANOGrav 15-year gravitational-wave background
methods. Physical Review D, 109(10), 103012.
Matichard, F., Lantz, B., Mittleman, R., et al., 2015.
Seismic isolation of Advanced LIGO: Review of
strategy, instrumentation and performance. Classical
and Quantum Gravity, 32(18), 185003.
Ni, W. T., 2024. Space gravitational wave detection:
Progress and outlook. Chinese Science Bulletin, 54,
270402.
Pitkin, M., Reid, S., Rowan, S., Hough, J., 2011.
Gravitational wave detection by interferometry (ground
and space). Living Reviews in Relativity, 14(5).
Ringwald, A., Tamarit, C., 2022. Revealing the cosmic
history with gravitational waves. Physical Review D,
106(6), 063027.
Schmidt, P., 2021. Gravitational waves from binary black
hole mergers: Modeling and observations. Living
Reviews in Relativity, 24(1), 1.
Yahalom, A., 2023. The weak field approximation of
general relativity and the problem of precession of the
perihelion for Mercury. Symmetry, 15(1), 39.
Yu, H., Lin, Z. C., Liu, Y. X., 2019. Gravitational waves
and extra dimensions: A short review. Communications
in Theoretical Physics, 71(8), 991.
Analysis of the Principle and the State-of-Art Results for Searching Gravitational Waves
179
