From Algebraic Synthesis and GRAFCET to Logical Controller

Design in ST Code (IEC 61131-3)

Mathieu Roisin

, Dimitri Renard

, David Annebicque

, Bernard Riera

and Pierre-Alain Yvars

CReSTIC, University of Reims Champagne-Ardenne, Reims, France

QUARTZ, ISAE-Supméca, Saint-Ouen, France

Keywords: PLC, Control Design, GRAFCET, Algebraic Synthesis.

Abstract: This paper addresses the problem of logic controller synthesis and the automatic generation of code compliant

with the IEC 61131-3 standard, specifically Structured Text (ST) code. From a methodological perspective,

two complementary approaches can be used to tackle this problem. The extensional approach explicitly

represents the solution using models such as GRAFCET or Petri nets. In contrast, the intensional approach

defines the solution space through a set of rules or constraints, without enumerating all possible solutions.

Among intensional techniques, algebraic synthesis stands out as a formal method to derive controllers from

specifications. We argue that combining extensional and intensional approaches leads to more efficient and

robust controller design. To this end, we propose a hybrid workflow that integrates an extensional model

(GRAFCET) with an intensional method (algebraic synthesis), enabling the automatic generation of IEC

61131-3 ST code. To support this workflow, we have developed two software tools: GReSTIC, for code

generation and simulation, and BooG, for the algebraic synthesis and fusion of the two approaches. The

proposed methodology is validated through a case study, demonstrating the automatic generation of reliable

and standard-compliant ST code.

1 INTRODUCTION

The advent of Industry 4.0 (Koren, 2010) is

transforming industrial system design and operation.

As production systems grow more complex, robust,

integrated, and automated methods are essential to

account for technical, logical, and physical

constraints early on. Automation relies on developing

reliable and safe logic controllers tailored to system

needs.

In this context, our work focuses on synthesizing

logic controllers and automatically generating PLC

code (Jones, 1998) compliant with IEC 61131-3

(John & Tiegelkamp, 2001) We explore intensional

approaches, which define control problems through

rules and constraints rather than explicitly

representing solutions (e.g., GRAFCET (IEC 60848,

https://orcid.org/0009-0009-7182-1205

https://orcid.org/0009-0009-2265-9176

https://orcid.org/0000-0002-0706-0714

https://orcid.org/0000-0003-1294-874X

https://orcid.org/0000-0002-7131-6796

2012) (Schumacher, 2013), or Petri nets (Teng &

Black, 1990), allowing solvers to compute solutions

without exhaustive enumeration. We argue that

integrating both extensional and intensional methods

enables more efficient and robust controller design.

This article is structured as follows. We first

present extensional and intensional approaches to

logic control synthesis, then focus on an intensional

method based on algebraic synthesis. Next, we

introduce a workflow combining GRAFCET

(extensional) and algebraic synthesis (AS)

(intensional) (Ranger, 2021), supported by two tools:

GReSTIC, for generating ST code from GRAFCET,

and BooG, for merging GRAFCET and AS results.

Finally, the workflow is applied to a case study,

generating ST code for a virtual PLC controlling a

simulated manufacturing system.

494

Roisin, M., Renard, D., Annebicque, D., Riera, B. and Yvars, P.-A.

From Algebraic Synthesis and GRAFCET to Logical Controller Design in ST Code (IEC 61131-3).

DOI: 10.5220/0013817800003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 494-501

ISBN: 978-989-758-770-2; ISSN: 2184-2809

2 MODELLING METHODS AND

TOOLS FOR LOGIC

CONTROLLER SYNTHESIS

According to the literature, there are two general

ways of solving a problem: by extension or by

intension (Peregrin, 2007). The distinction lies in how

the set of possible solutions is represented and

processed.

The extensional approach explicitly describes

candidate solutions. In logic controller design,

GRAFCET diagrams graphically specify action

sequences and transitions, representing a concrete

solution.

In contrast, the intensional approach specifies

rules or constraints that valid solutions must satisfy

without enumerating them. In controller synthesis,

algebraic modeling expresses desired behavior as

logical constraints, and a solver generates correct-by-

construction implementations.

Logic controller design can use extensional,

intensional, or both approaches. Extensional methods

are directly interpretable and align with industry,

while intensional methods offer flexibility and

automation for complex systems. Combining them

leverages both strengths for more efficient and

reliable control logic synthesis.

This dual perspective lays the foundation for the

methodology proposed in this paper, which leverages

both extensional and intensional models to support

automated and robust controller generation.

2.1 Extensional Approach

Extensional logic controller design involves formally

specifying a candidate solution, including system

states and transitions, and systematically verifying its

behavior against functional and safety requirements.

GRAFCET (Schumacher, 2013), Petri nets (Teng &

Black, 1990) and state machines (Rabin & Scott,

1959) are all based on this approach, which is widely

used to control discrete-event systems. Today, this

method is the most widely used in the industrial world

2.2 Intensional Approach

The intensional approach to logic controller design

consists in formulating system requirements as a set

of constraints on variables representing the unknowns

of the problem. One or more admissible solutions can

then be generated using an automatic solver, which

ensures that each solution satisfies all the defined

constraints.

In the field of automation engineering, methods

such as Supervisory Control Theory (SCT) (Ramadge

& Wonham, 1987) or Algebraic Synthesis (AS)

(Hietter, 2009) follow this intensional paradigm.

However, these methods are still rarely used in

industry, where they are often overshadowed by more

operational, but often empirical, extensional

approaches.

A key advantage of intensional methods is that

they guarantee correct solutions: if the specification

is valid, any derived solution satisfies it.

2.3 Advantages and Disadvantages

Both extensional and intensional approaches have

advantages and limitations. Extensional methods use

intuitive graphical models and generate logic

efficiently implementable on a PLC, but require

manually specifying a single solution, which is error-

prone, needs to be verified (e.g., GRAFCET

verification, Roussel & Lesage, 1996), and hard to

generalize. Intensional methods are declarative and

provide formally correct solutions, but defining

constraints is complex, PLC implementation can be

less efficient, and sequential or procedural behaviors

are harder to represent.

Given their complementary strengths, we propose

combining extensional and intensional approaches.

GRAFCET handles simple action sequences well,

while intensional methods better address complex

requirements like safety constraints or task

synchronization.

3 ALGEBRAIC SYNTHESIS OF

LOGICAL CONTROLLER

In this section, we discuss the algebraic synthesis

(AS) method, which plays a key role in the broader

workflow that will be presented later in this paper.

Algebraic synthesis uses an intensional approach,

defining constraints over known variables (e.g.,

sensors) and unknown variables (e.g., actuators) to

identify all valid solutions (by solving the problem).

Developed for controller synthesis, it expresses

output variables as logical functions of inputs and

internal states (Hietter, 2009) (Roussel & Lesage,

2012) (Roussel & Lesage, 2014).

3.1 Fundamental Principles

The algebraic synthesis (AS) method is based on

From Algebraic Synthesis and GRAFCET to Logical Controller Design in ST Code (IEC 61131-3)

495

Boolean algebra. It operates over a set of Boolean

variables divided into two categories:

- Known Variables: Read-only inputs, such as

sensors or previous controller states.

- Unknown Variables: Write-only outputs, such as

actuators or internal controller states.

A set of Boolean constraints is defined over these

variables using connectors (equality (=), implication

(=>)) and logical operators (OR (+), AND (.) and

NOT (-). The goal of algebraic synthesis is to

compute all Boolean expressions for each unknown

variable as a function of the known variables, in such

a way that all constraints are satisfied.

The method consists of different steps presented

in the (Hietter, 2009) thesis. In the end each unknown

variable is ultimately expressed as a function of

known variables and a set of Boolean parameters.

Different parameter values yield different solutions.

The complete set of parameter assignments represents

all possible solutions that satisfy the original

constraints.

To select a unique, implementable PLC solution,

Boolean parameters must be defined either by an

expert or via formal methods such as Boolean

lexicographic optimization (Marques-Silva, 2011).

Boolean lexicographic optimization (Leroux,

2010) (Leroux & Roussel, 2012) lets users define

Boolean objectives, and the solver assigns parameter

values to optimize them in order, ensuring a correct

and design-optimized solution.

3.2 Problem Modelling

For any problem, we consider the following elements:

• Unknown Boolean Variables: PLC outputs

(actuators) and internal controller states.

• Alias Boolean Variables: named

expressions to simplify constraints.

• Known Boolean Variables: PLC inputs

(sensors) and previous controller states.

• Constraints involving these variables.

The constraints can be of the following types:

• Equality Constraint: Equality between two

Boolean expressions.

• Alias Constraint: Assigns a Boolean

expression to an alias variable, which is

replaced by the expression during solving.

• Implication Constraint: A logical

implication between two Boolean

expressions.

These constraints (excluding alias constraints) can be

classified into two categories:

• Assumptions: Involve only known

variables and are assumed to hold, ensuring

a solution exists.

• Constraints to be Solved: Involve

unknown variables and must be satisfied to

compute their values.

Unless explicitly restricted by assumptions,

known variables are considered free (0 or 1). In some

cases, this can lead to combinations of known

variable values for which no valid solution exists. To

avoid this, additional assumptions may be required

to restrict the value of the known variables and avoid

"no solution" cases.

The model can also determine a unique solution

by defining an optimization order over Boolean

expressions. Parameters introduced during synthesis

are then assigned values that respect this order,

yielding the most desirable solution.

3.3 Solving with a Solver

After modeling the problem, the BESS solver

(Boolean Equation System Solver) can be used to

compute a solution. The problem model must be

expressed in the BESS format, which is specifically

designed for algebraic synthesis based on Boolean

logic.

Figure 1 illustrates an example of a model written

in BESS format. Operators AND, OR and NOT are

respectively represented by “.”, “+” and “/”. Logical

connectors equality and implication are represented

by “=” and “<=”.

The solver applies algebraic synthesis principles,

including variable substitution. It checks for

solutions, then computes unknowns as functions of

known variables and Boolean parameters. If an

Figure 1: Example of a BESS model.

#Name:[Unknown|Known|Alias](*Optional comment *);

Y : Unknown (**) ;

</SYMBOLS>

# Name = BooleanFormula (* Optional comment *) ;

</ALIASES>

# Name : BooleanFormula [=<|=] BooleanFormula (*

Optional comment *) ;

R1 : (**) Y <= 1;

</REQUIREMENTS>

# Name : [Minimal|Maximal] (* Comment *)

M1 : Maximal (**) Y;

</OPTIMUM CRITERIA>

</PROBLEM>

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

496

optimization strategy is defined, it assigns parameter

values accordingly to select a solution. The solver

thus returns one or more correct-by-construction

solutions that satisfy the constraints and any

optimization objectives.

4 WORKFLOW TO MODEL A

PROBLEM USING ALGEBRAIC

SYNTHESIS AND GENERATE

ST CODE

4.1 Modelling Steps

To solve a logic controller synthesis problem, it is

first necessary to define a formal model representing

the problem. The proposed method is based on a

hybrid approach combining:

• an extensional representation using a

GRAFCET model,

• and an intensional representation using

algebraic synthesis techniques.

These two representations are then integrated to

automatically generate Structured Text (ST) code.

4.2 Workflow for Generating ST Code

that Can Be Executed by a PLC

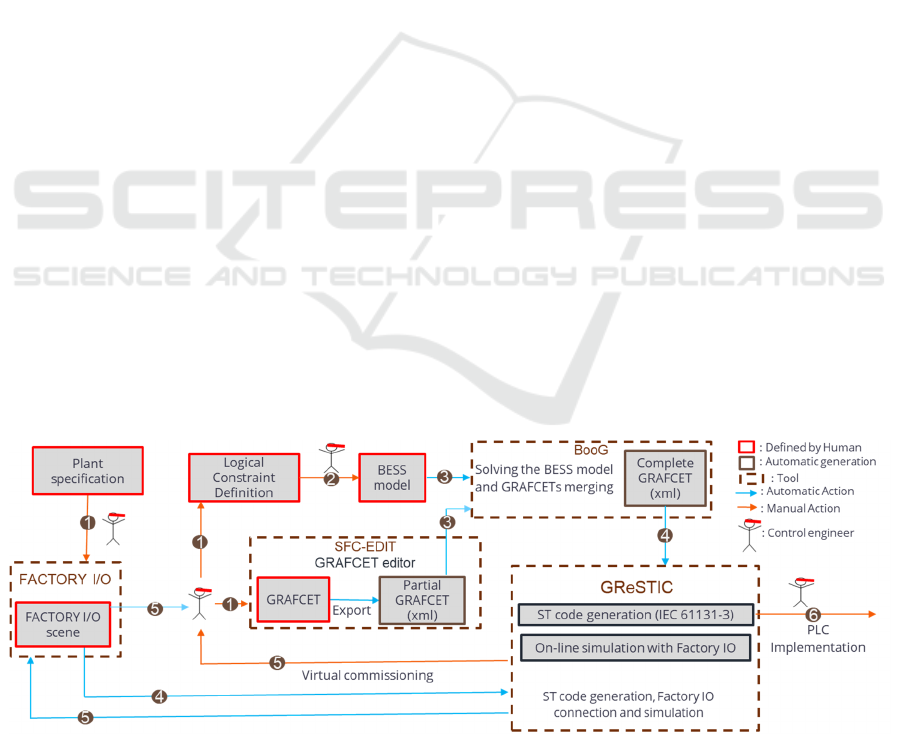
The proposed workflow (see Figure 2) allows logic

control problems to be addressed by combining

intensional and extensional methods. It is

structured into six main steps:

1. Specification of the Logic Controller

The first step defines the controller’s behavior using

extensional and/or intensional approaches. The

extensional part is modeled in SFC-EDIT, which

edits and exports GRAFCETs in XML, while the

intensional part specifies logical constraints from

functional requirements and solves them

algebraically (Hietter, 2009). The controller then

operates on a physical or virtual system, whose

operational part (OP) is modeled, in our case, using

Factory I/O (Riera & Vigario, 2017).

2. Modeling in BESS Format.

The logical constraints are translated into a model

written in BESS (Boolean Equation System Solver)

format (Ranger, 2022).

3. Algebraic Synthesis and GRAFCETs Merging.

The BooG tool, developed in-house, uses the BESS

solver for algebraic synthesis. The solution is

converted into a GRAFCET (XML format) and

merged with fragments from the extensional

approach, producing a complete and consistent

GRAFCET model.

4. ST Code Generation.

The GReSTIC software, also developed in our

laboratory, generates ST (Structured Text) code for

the logic controller from the Factory I/O (Riera &

Vigario, 2017) scene and the complete GRAFCET

model in XML format.

5. Virtual Commissioning

GReSTIC includes a soft PLC for simulating the

controller and interacting in real time with Factory

I/O, enabling virtual commissioning to test and

validate the control logic before deployment.

6. Deployment on a Physical PLC

Once validated, the ST code can be deployed on a real

PLC, ensuring consistency between simulation and

operation.

Figure 2: Workflow for ST code generation from algebraic synthesis (AS) and GRAFCET.

From Algebraic Synthesis and GRAFCET to Logical Controller Design in ST Code (IEC 61131-3)

497

5 SOFTWARE TOOLS

5.1 GReSTIC Software

GReSTIC (GRAFCET to ST, Integration, and

Commissioning) is a code generator and simulator for

Structured Text (ST), based on GRAFCET

specifications, developed in the laboratory. GReSTIC

is a Windows application developed in C# using the

.NET Framework 4.8.

As input, it uses a GRAFCET specification

described in an open XML format. The tool used to

graphically represent GRAFCETs is called SFCEdit.

This editor was chosen because of its ability to export

to an open XML format and its compliance with the

standard (International Electrotechnical Commission,

2013b).

GReSTIC has a strong integration with the

Factory-I/O simulator, abstracting the configuration

of communication driver settings. The GRAFCETs

contained in the XML file are analyzed, and the

communication driver information from the Factory-

I/O scene is incorporated. PLC code in Structured

Text (ST) is then generated. This code can be either

simulated directly within the integrated simulator or

exported to various software targets.

5.2 BooG Software

BooG (Renard, 2024) is an application that enables

the transcription of the resulting unknown equations

from BESS into a format compatible with GReSTIC.

It is a Python-based application provided as an

executable with a graphical user interface to improve

user experience. It is configured by entering two

fields: one corresponding to the BESS file and the

other to the export from SFCEdit in XML format. The

insertion index allows placing the filter generated by

BESS at a specific location within the set of

GRAFCETs contained in the SFCEdit XML

specification file.

As input, the specification file to be solved by

BESS must be provided. Additionally, an optional file

exported from SFCEdit can be included. After BESS

solves the system of equations, the equations are

retrieved and transformed into GRAFCET format.

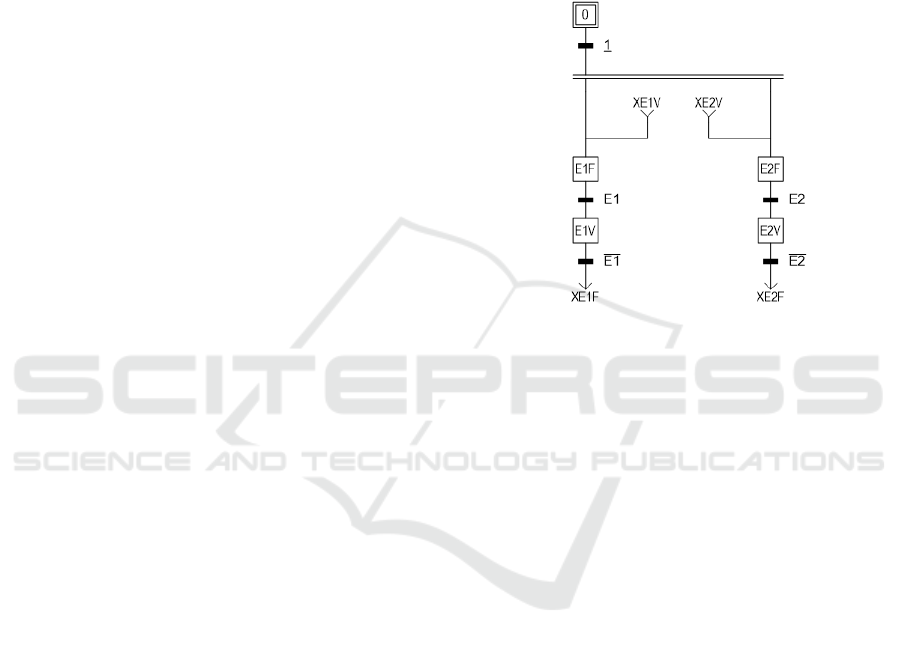
Figure 3 illustrates the GRAFCET model used to

integrate the equations produced by BESS (example

with two equations). For each equation returned in the

solution by BESS, two GRAFCET steps are created,

one representing the equation being true and the other

representing it being false. Two transitions allow

looping between the true and false states. These

transitions respectively correspond to the equation

and its negation. In this way, the equation is

represented in GRAFCET form. This step-based

representation makes it possible to position the

equations precisely within the program. In contrast,

representing equations as actions would imply that

they are calculated at the end of the cycle. The symbol

E1V corresponds to the symbol of the unknown

associated with the equation. Thus, as soon as the step

is evaluated, its value is already updated for the rest

of the ongoing cycle's calculations.

Figure 3: GRAFCET model generated by BooG.

The resulting GRAFCET is returned to the user.

If an SFCEdit file has been provided, the generated

GRAFCET is inserted into the set of GRAFCETs in

the SFCEdit file at the specified position.

6 CASE STUDY

We illustrate our approach to algebraic synthesis

using a system involving the crossing of two

conveyors (see Figure 4 from the Discrete Event

System (SED) 2023 school (Riera & Renard, 2024)).

Each flow is regulated by a traffic light (red or green),

and pallets must wait for a green light before crossing

the shared zone, which is made accessible by a

turntable. This example is a simple proof of concept

in order to demonstrate the proposed workflow.

Two sensors indicate the position of the turntable:

• TTLimit12: Turntable is in position 12

• TTLimit34: Turntable is in position 34

Pallets are autonomous—meaning they stop when

the light is red and proceed when it is green. This

behavior is implemented via a dedicated control

(described in GRAFCET, see Figure 5), which

manages the back-and-forth movement of the two

pallets. The intent to cross is represented by four

GRAFCET steps: XR12, XR21, XR34, and XR43.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

498

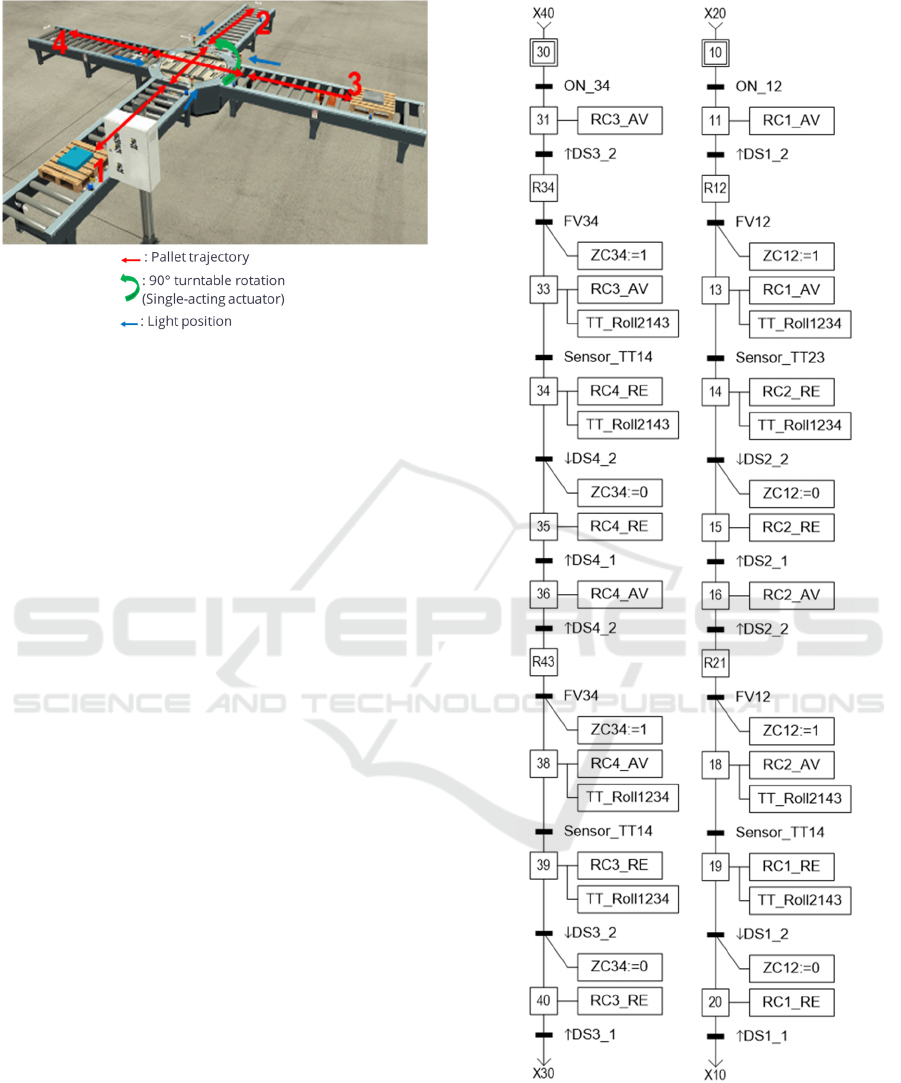
Figure 4: Case study system.

Two global variables (ZC12, ZC34) indicate the

presence of a pallet in the shared area. A user-

activated button determines the default position of the

turntable (ValDefaut).

Nine actuators must be controlled, including the

green/red traffic lights and the turntable actuator:

• Traffic lights: FV12, FR12, FV21, FR21,

FV34, FR34, FV43 and FR43

• TTTurn: Single-acting turntable rotation

(Active = position 12, Inactive = position

34)

The control objective is to synchronize the lights

and turntable to avoid collisions, while ensuring the

automatic return of the turntable to its default position

(ValDefaut = 0 corresponds to turntable position 34).

6.1 Bess Model Creation

In the Algebraic Synthesis (AS) formalism, the

problem is reduced to constraints from requirements

and assumptions, with a solution criterion usually

maximizing unknown variables.

For the case study, we defined fifteen requirement

constraints, three assumption constraints, and four

maximization constraints to ensure a unique solution

(see Figure 6). Currently, no method exists to

systematically derive the constraint set directly from

the requirements.

Figure 5: Pallets control GRAFCET.

From Algebraic Synthesis and GRAFCET to Logical Controller Design in ST Code (IEC 61131-3)

499

Figure 6: Extraction of the BESS constraint model for the

case study problem.

6.2 BooG Software Solving

We obtained this set of Boolean expressions (Figure

) using the BooG software to solve the BESS model

of the case study for each unknown variable

(intermediate and actuator variables) in terms of

known variables (sensors and GRAFCET states).

Then, by merging the BESS model solution with

the pallet control GRAFCET, we obtain a complete

GRAFCET, This complete GRAFCET is not

intended for human reading.

Figure 7: Algebraic Synthesis solution.

6.3 ST Code Generated from GReSTIC

Using GReSTIC, we generate ST code from the

complete GRAFCET and the Factory I/O scene. Its

PLC simulator interacts with Factory I/O, allowing us

to validate the constraints used in the model. The

solution for this case study is valid. A video

demonstrates the full workflow from the BESS model

to simulation: https://youtu.be/Q6IbG3DUudY

6.4 Case Study Conclusion

The workflow combines intensional (SA) and

extensional (GRAFCET) approaches for controller

synthesis. The BESS model from the intensional part

is automatically solved and merged with the

GRAFCET to generate ST code that can be used in an

API. We can simulate that ST code on the Factory I/O

scene to evaluate the validity of the model.

7 CONCLUSION AND OUTLOOK

This paper presented a workflow combining algebraic

synthesis with extensional modeling (GRAFCET) for

logic controller synthesis. Controller specifications

are defined via a BESS model and a GRAFCET

diagram. BooG software automatically solves the

BESS model and integrates it with the GRAFCET,

while GReSTIC software uses the combined

GRAFCET and a Factory I/O scene to generate ST

(*----------------Constraints------------------*)

(*Red light opposite of green light*)

FV12 = /(FR12); FV34 = /(FR34);

(*Can have green light in direction X if pallet in commo

zone (ZC) with direction X or if authorizing the pallet with

direction X to go in the common zone AND if the

Turntable is in the X position*)

FV12 <= (TTLimit12 . (AUT12 + ZC12));

FV34 <= (TTLimit34 . (AUT34 + ZC34));

(FV12 . FV34) = 0; (*Cannot have both green light*)

(*If a pallet is in the ZC with X direction then the X gree

light must be on*)

(ZC12 . /(FV12)) = 0; (ZC34 . /(FV34)) = 0;

(*The turntable turn (actuator) according to the directio

of the pallet in ZC or the authorized direction*)

(ZC12 + AUT12) <= TTTurn;

(ZC34 + AUT34) <= /(TTTurn);

(*Can have an authorization of a pallet in direction X if

pallet wants to cross the turntable in direction X AND i

there is not a pallet in ZC in the other direction AND if we

don’t authorize the pallet in the other direction to cross*)

AUT12 <= (((XR12 + XR21) . /(ZC34)) . /(AUT34));

AUT34 <= (((XR34 + XR43) . /(ZC12)) . /(AUT12));

(*The light value in a direction are the same*)

FV21 = FV12; FR21 = FR12;

FV43 = FV34; FR43 = FR34;

(*-----------------Assumptions---------------*)

(TTLimit34 . TTLimit12) = 0;(*Cannot have the turntable

in both position at the same time*)

(ZC12 . TTLimit34) + (ZC12 . /(TTLimit12)) + (ZC34 .

/(TTLimit34)) + (ZC34 . TTLimit12)) = 0; (*Necessary

hypothesis for coherence.*)

(*---------Maximization-----------*)

M0 : Maximal (*Maximize authorization of a pallet in the

34 direction*)

AUT34;

M1 : Maximal (*Maximize authorization of a pallet in the

12 direction*)

AUT12;

M2 : Maximal (*Maximize the green lights on*)

FV12 + FV34;

M3 : Maximal (*Maximize default position*)

TTTurn . ValDefaut +/TTTurn . /ValDefaut;

FV12 = ZC12+TT_Limit12.XR12./XR34./XR43

+TT_Limit12./XR34./XR43.XR21

FV34 = ZC34+TT_Limit34.XR34+TT_Limit34.XR43

FR12 = ZC34+TT_Limit34+/TT_Limit12+

/ZC12.XR34+/ZC12.XR43+/ZC12./XR12./XR21

FR34 = ZC12+/TT_Limit34+TT_Limit12

+/ZC34./XR34./XR43

FV21 = ZC12+TT_Limit12.XR12./XR34./XR43

+TT_Limit12./XR34./XR43.XR21

FV43 = ZC34+TT_Limit34.XR34+TT_Limit34.XR43

FR21 = ZC34+TT_Limit34+/TT_Limit12+/ZC12.XR34 +

/ZC12.XR43+/ZC12./XR12./XR21

FR43 = ZC12+/TT_Limit34+TT_Limit12

+/ZC34./XR34./XR43

TT_Turn = ZC12+/ZC34.XR12./XR34./XR43

+/ZC34./XR34./XR43.XR21

+/ZC34./XR34./XR43.ValDefaut

AUT12 = ZC12.XR12+ZC12.XR21

+/ZC34.XR12./XR34./XR43+/ZC34./XR34./XR43.XR21

AUT34 = /ZC12.XR34+/ZC12.XR43

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

500

code, which can then be implemented on a PLC and

simulated.

The current approach lacks a structured

representation, relying on variables and Boolean

constraints that are hard to interpret for new users..

Understanding the complete system based solely on

these constraints and variables can be challenging.

Since the BESS model uses problem-specific

constraints, adding new requirements often requires

major changes, limiting extensibility and

generalizability.

We argue that overcoming these limitations

requires a structured approach for constructing a

generic set of elements and structured constraints

with a generic language adapted to any logic

controller synthesis problem. This approach involves

a clear definition and application of various types of

constraints to the distinct components of the

controller synthesis problem.

ACKNOWLEDGEMENTS

This research was funded by the French National

Research Agency (ANR) under the Digital Twins for

Cyber-Physical Systems project (ANR-23- CE10-

0010-01). The authors would like to thank the ANR.

REFERENCES

Hietter, Y. (2009). Synthèse algébrique de lois de

commande pour les systèmes à évènements discrets

logiques. Phd. École normale supérieure de Cachan -

ENS Cachan.

IEC 60848, (2012). GRAFCET specification language for

sequential function charts. (3rd ed.).

John, K.-H., & Tiegelkamp, M. (2001). IEC 61131-3:

Programming Industrial Automation Systems.

Springer.

Jones, C. T. (1998). Programmable Logic Controllers: The

Complete Guide to the Technology. Brilliant-Training.

Koren, Y. (2010). The Global Manufacturing Revolution:

Product-Process-Business Integration and

Reconfigurable Systems. John Wiley & Sons.

Leroux, H. (2011) Algebraic Synthesis of Logical

Controllers with Optimization Criteria. ENS Cachan,

Cachan, France.

Leroux, H., & Roussel, J. -M. (2012) Algebraic synthesis

of logicalcontrollers with optimization criteria.

Proceedings of the 6th International Workshop on

Verification and Evaluation of Computer and

Communication Systems (VECOS ’12), pp. 103–114.

Marques-Silva, J., et al (2011). Boolean lexicographic

optimization: algorithms & applications. Annals of

Mathematics and Artificial Intelligence, pp. 317-343.

Peregrin, J. (2007). Extensional vs. Intensional Logic. In

Philosophy of Logic (pp. 913-942). Elsevier.

Rabin, O. M., & Scott, D. (1959). Finite Automata and

Their Decision Problems. IBM Journal of Research and

Development, pp. 114-125.

Ramadge, P. J., & Wonham, W. M. (1987). Supervisory

Control of a Class Of Discret Event Processes. SIAM

Journal on Control and Optimization, pp. 206-230.

Ranger, T., et al (2021). Manufacturing Tasks

Synchronization by Algebraic Synthesis. 4th IFAC

Conference on Embedded Systems, Computational

Intelligence and Telematics in Control CESCIT 2021,

pp. 226-231.

Ranger, T. (2022). Approche par synthèse algébrique et

filtre logique pour la commande des systèmes

manufacturiers cyber-physiques. Phd. Université de

Reims Champagne-Ardenne, Reims.

Renard, D., et al (2024). From Reinforcement Learning to

Reality: Generating Structured Text Logic Controller.

2024 10th International Conference on Control,

Decision and Information Technologies (CoDIT), pp.

1269-1274.

Riera, B., & Renard, D. (2024). École SED et plateforme de

formation en ligne : une dynamique pour la diffusion

des systèmes à événements discrets https://fad.univ-

lorraine.fr/pluginfile.php/158867/mod_label/intro/UT

L_CTRL_SA_Application.pdf

Riera, B., & Vigario, B. (2017). HOME I/O and FACTORY

I/O: a virtual house and a virtual plant for control

education. 20th IFAC World Congress, pp. 9144-9149.

Roussel, J.-M., & Lesage, J. (1996). Validation and

verification of grafcets using state machine.

Proceedings of IMACS-IEEE ”CESA'96”, pp. 758-764.

Roussel, J.-M., & Lesage, J.-J. (2012). Algebraic synthesis

of logical controllers despite inconsistencies in

specifications. IFAC Proceedings Volumes, pp. 307-

314.

Roussel, J.-M., & Lesage, J.-J. (2014). Design of Logic

Controllers Thanks to Symbolic Computation of

Simultaneously Asserted Boolean Equations.

Mathematical Problems in Engineering, pp. 1-15.

Schumacher, F., et al (2013). Tool support for an automatic

transformation of GRAFCET specifications into IEC

61131-3 control code. 2013 IEEE 18th Conference on

Emerging Technologies & Factory Automation

(ETFA).

Teng, S.-H., & Black, J. T. (1990). Cellular manufacturing

systems modeling: The Petri net approach. Journal of

Manufacturing Systems, pp. 45-54.

From Algebraic Synthesis and GRAFCET to Logical Controller Design in ST Code (IEC 61131-3)

501