Prediction of Urban Population Growth in Zhengzhou City Based on

Time Series Analysis

Yushi Gan

Faculty of Science and Technology, Beijing Normal-Hong Kong Baptist University, Zhuhai, Guangdong, China

Keywords: Urban Development, Population Growth, ARIMA Model, Time Series Analysis.

Abstract: Population dynamics represent one of the most critical issues in human society. Population growth

significantly influences economic and social development, impacting employment, innovation, and urban

competitiveness. Consequently, analyzing population trends and forecasting future changes can provide

valuable insights into developmental needs and offer a scientific foundation for economic planning, social

progress, and urban design. This study conducts an in-depth analysis of Zhengzhou City's population data

from 1982 to 2022 using the Autoregressive Integrated Moving Average (ARIMA) model based on annual

statistics released by the Zhengzhou Municipal Bureau of Statistics. It further predicts the population growth

trajectory for the next decade. The Ljung-Box test results indicate that the residuals of the ARIMA (1,2,1)

model exhibit no significant autocorrelation and approximate white noise, demonstrating the model's robust

predictive capability. Projections suggest that Zhengzhou's population will maintain steady growth in the

coming years, with the permanent resident population surpassing 15 million by 2032. However, the long-term

population growth in Zhengzhou faces numerous challenges and uncertainties due to factors such as limited

resource capacity, economic fluctuations, industrial restructuring, regional competition, and policy

adjustments.

https://orcid.org/0009-0007-8998-3515

1 INTRODUCTION

Population has consistently been a fundamental,

global, long-term, and strategic factor in national

development. Factors such as population size,

structure, distribution, and quality are critical national

conditions influencing the economic and social

development of a country (Xi, 2020). Accurately

forecasting population growth trends is essential for

formulating scientific population policies, optimizing

resource allocation, and enhancing competitiveness.

Zhengzhou, designated as the core city of the Central

Plains Economic Zone by the State Council, plays a

pivotal role in driving regional development and

exerting significant radiation effects on surrounding

cities. In recent years, the central and western regions

have experienced a notable phenomenon of

population return, injecting new vitality into

Zhengzhou's development and profoundly impacting

its population growth (Zou, 2024). As of the end of

2023, Zhengzhou's permanent population reached

13.008 million (Zhengzhou Bureau of Statistics,

2024). Therefore, predicting population growth in

Zhengzhou holds great significance for studying the

development of Zhengzhou and even the broader

central and western regions.

In the context of accelerating global urbanization,

urban population growth serves as a key indicator

reflecting the vitality and potential of urban

development, attracting considerable attention from

both academic and urban planning fields.

Geographically weighted regression models and

spatial correlation were used by Jia & Guo (2025) to

examine the spatial heterogeneity of influencing

factors in Henan Province's county-level cities in

2010 and 2020. Their study revealed that the floating

population exhibited significant areal bias and

accelerated concentration toward central cities.

Zhang and colleagues (2024) employed logistic

mathematical models to determine the permanent

population growth rate in Henan Province's several

counties (districts). They looked at the features of the

permanent population growth rate's regional

distribution in Henan Province using hotspot and

Gan, Y.

Prediction of Urban Population Growth in Zhengzhou City Based on Time Series Analysis.

DOI: 10.5220/0013813800004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 47-52

ISBN: 978-989-758-774-0

spatial semivariance function analysis. According to

the findings, the north and center of Henan Province

had greater regional permanent population growth

rates than the south and surrounding areas. There is a

significant correlation between the degree of

economic growth and the siphon impact that urban

built-up regions, especially newly developed zones,

have on the local people. Feng (2024) proposed

constructing an evaluation index system for

Zhengzhou's competitiveness as a national central

city, emphasizing technological innovation,

industrial transformation, opening up to external

influences, and management services. A relevant

official from the Henan Provincial Bureau of

Statistics noted that Zhengzhou's population size

changes exhibited two primary characteristics: strong

absorption capacity and high agglomeration levels

(Zhengzhou Daily, 2021).

Previous studies by scholars have predominantly

focused on existing data to explore the

spatiotemporal characteristics of Zhengzhou's

population. However, few predictive planning

suggestions have been proposed to enhance

Zhengzhou's economic development and urban

influence. This study aims to employ time series

analysis methods to conduct in-depth research on

Zhengzhou City's population growth over the years,

make more precise predictions regarding future

population growth trends, provide a scientific basis

for urban development, and support Zhengzhou's

sustainable and healthy development.

2 RESEARCH METHODS

2.1 Data Source and Explanation

The data utilized in this study were sourced from the

official website of the Zhengzhou Municipal Bureau

of Statistics, specifically the dataset titled "Annual

Population" (Zhengzhou Municipal Bureau of

Statistics, 2023). This dataset has been adjusted

according to the results of China's seventh national

population census, ensuring its high reliability,

accuracy, broad survey scope, extensive sample size,

and authoritative nature, all of which align with

international standards.

This research collected population data for

Zhengzhou City spanning from 1982 to 2022,

resulting in a total of 41 observed data points. The

annual population growth rate was subsequently

calculated, yielding an additional 41 derived data

points. By employing time (year) as the horizontal

axis and total population (in units of 10,000 people)

and population growth rate (%) as the left and right

vertical axes, respectively, the aforementioned data

were visualized as time series graphs depicting the

historical population numbers and growth rates of

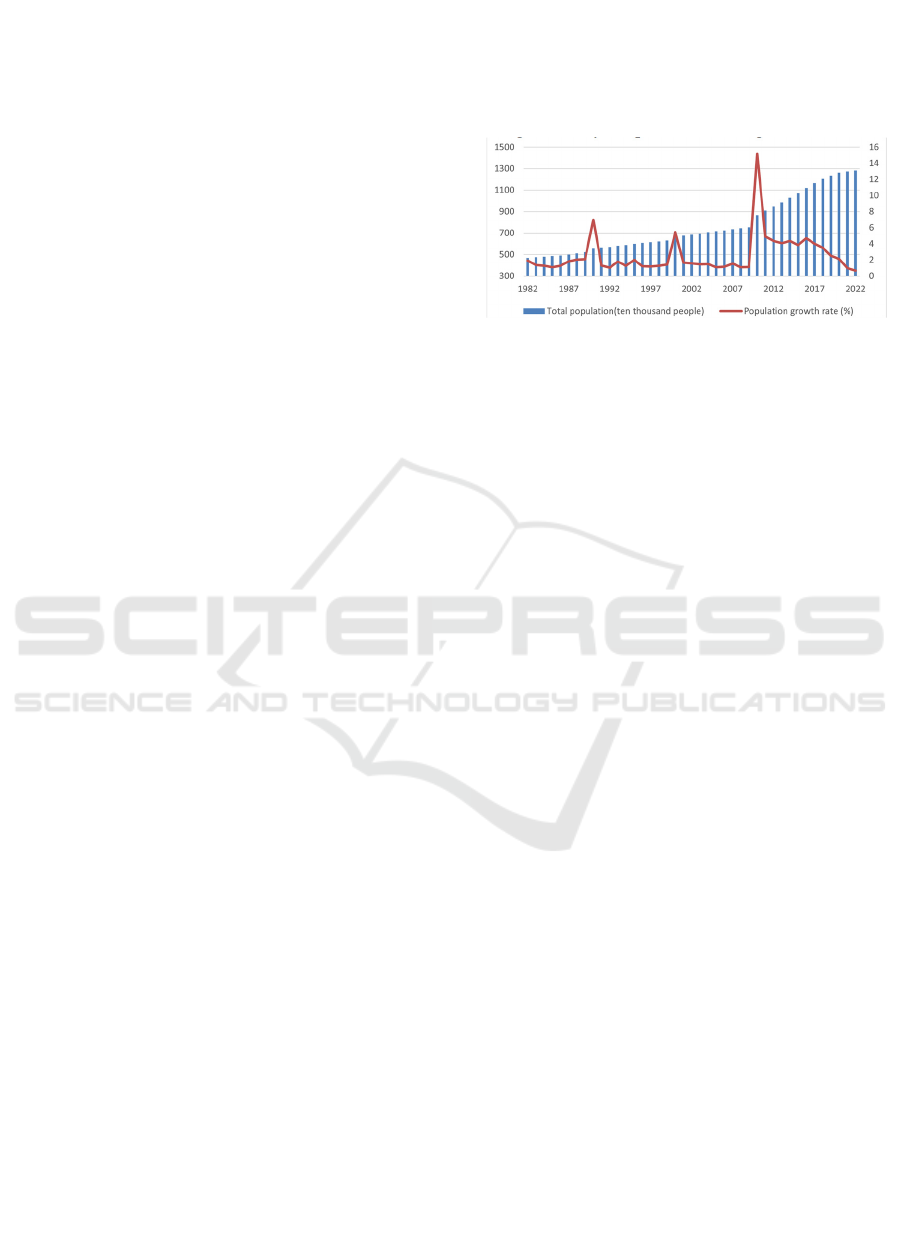
Zhengzhou City, as presented in Figure 1.

Figure 1: Historical Population and Population Growth

Rate of Zhengzhou (Photo/Picture credit: Original).

As illustrated in Figure 1, the population of

Zhengzhou City has exhibited a steady increase over

time, demonstrating a gradually stabilizing trend.

Notably, the population growth rate fluctuates

significantly across different years, with certain

periods experiencing notably higher growth rates

compared to others. Furthermore, the growth rate has

shown a downward trend in recent years.

2.2 Introduction to Research Methods

The Autoregressive Integrated Moving Average

model (ARIMA) is a classical time series forecasting

model renowned for its ability to manage time series

data that is not stationary. It offers flexible parameter

adjustments, a robust statistical theoretical

foundation, high computational efficiency, and

excellent interpretability. The ARIMA model is

particularly suited for stationary or nearly stationary

time series data and comprises three key components:

autoregression (AR), differencing (I), and moving

average (MA). Autoregression captures the linear

relationship between current observations and past

observations, differencing involves transforming the

original time series into a stationary one through

differentiation, and the linear connection between

present and historical observation error is shown in

the moving average. The standard notation for the

ARIMA model is ARIMA(p, d, q), where p stands for

the autoregressive order (the quantity of lag items in

AR), d denotes the differencing order (the number of

differencing operations), and q signifies the moving

average order (the number of lagged items in MA).

The modeling process of the ARIMA model includes

selecting appropriate values for p, d, and q, fitting the

model, and conducting residual analysis.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

3 STATISTICAL ANALYSIS

3.1 Stability Test

The ARIMA model requires that the time series be

stationary, meaning that its statistical characteristics,

such as mean, variance, and autocorrelation, remain

constant over time. This requirement ensures the

reliability of parameter estimation and the accuracy

of model predictions while avoiding spurious

regression and enhancing prediction precision. The

ADF test determines whether a sequence is stationary

by checking for the presence of unit roots within the

sequence.

In this study, the null hypothesis of the ADF test

posits that the time series contains a unit root and is,

therefore, non-stationary. The Dickey-Fuller statistic

obtained from the test results was -1.4026, having a

matching p-value of 0.8085. The null hypothesis

cannot be rejected since the p-value is greater than the

often-used significance level of 0.05, suggesting that

the population sequence being studied may not be

non-stationary, indicating that the population

sequence under investigation may be non-stationary.

Consequently, directly applying ARIMA modeling

would result in inaccurate predictions. To ensure the

reliability of the results, it is necessary to perform

differential processing on the original population

series, thereby removing the linear growth trend over

time, eliminating periodic fluctuations, and

transforming the series into a stationary one.

3.2 Differential Processing

The principle of differencing involves utilizing the

difference between consecutive time points (t and t-1)

in the time series to render a non-stationary sequence

stationary. In this study, first-order and second-order

differencing were applied to the original population

series of Zhengzhou, followed by stationarity testing

of the results. After first-order differencing, the

p-value stayed at 0.5381, which is much higher than

the generally accepted significance level of 0.05,

indicating that the sequence is still non-stationary and

necessitates second-order differencing. Following

second-order differencing, the p-value decreased to

0.0304, which is below 0.05, confirming that the

original sequence has been successfully transformed

into a stationary sequence through second-order

differencing. The corresponding stationarity test

results for the differencing orders are summarized in

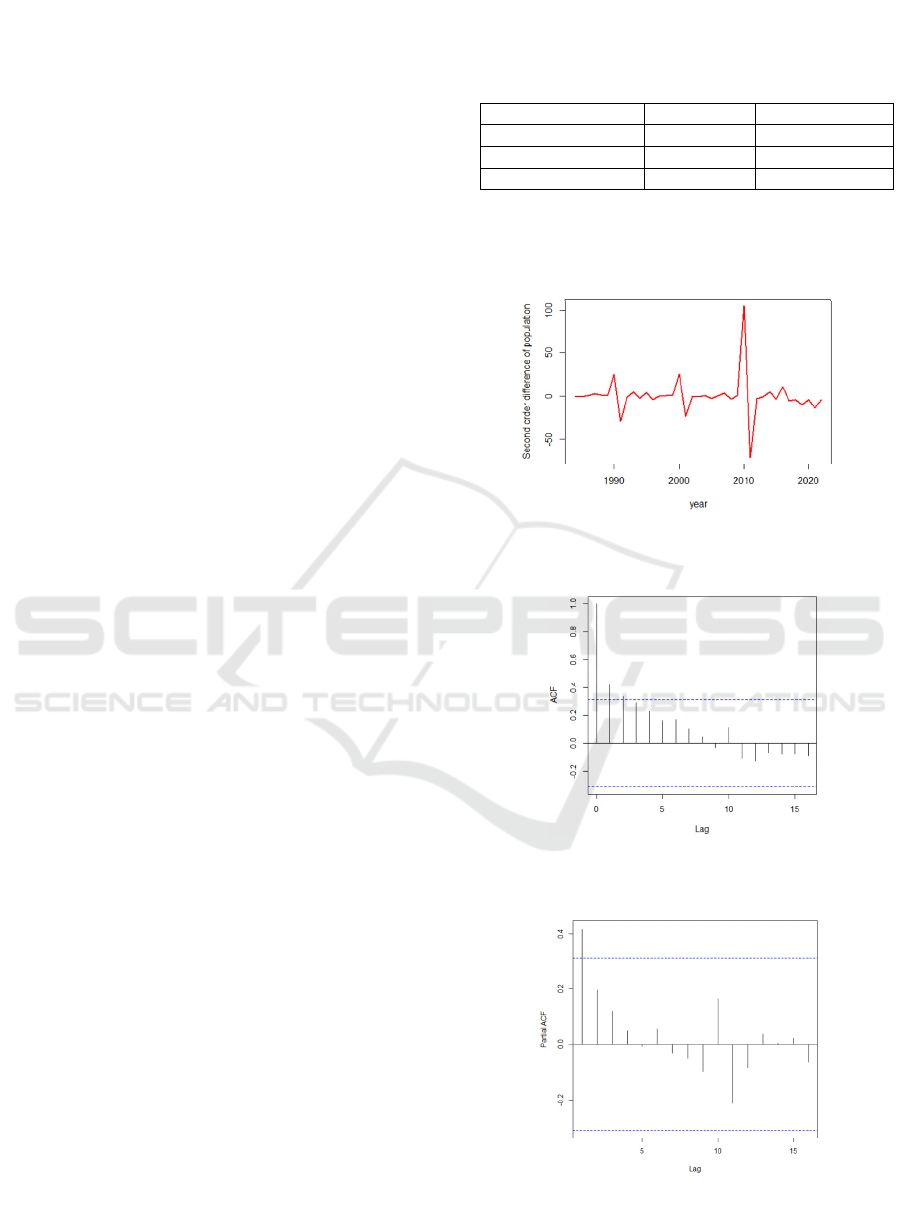
Table 1. The time series chart of Zhengzhou's

population after second-order differencing is

depicted in Figure 2.

Table 1: Results of Stability Test.

Difference orde

t-value

-value

0 -1.4026 0.8085

1 -2.0901 0.5381

2 -3.8016 0.0304

3.3 Model Establishment and

Parameter Estimation

Figure 2: Time Series Diagram After Second-Order

Differencing (Photo/Picture credit: Original).

Figure 3: Autocorrelation Function Diagram (Photo/Picture

credit: Original).

Figure 4: Partial Autocorrelation Function Diagram

(Photo/Picture credit: Original).

Prediction of Urban Population Growth in Zhengzhou City Based on Time Series Analysis

In this study, three primary parameters were

established based on the ARIMA model: the order of

autoregressive (AR) terms is denoted by parameter p,

the number of differences (I) by parameter d, and the

order of moving average (MA) terms by parameter q.

The degree of differencing d has been processed for

the original sequence in the previous text, resulting in

a value of 2. Subsequently, autocorrelation function

(ACF) and partial autocorrelation function (PACF)

are used to fit p and q. The ACF is typically

determined by observing the rate at which the

autocorrelation coefficient decreases as the lag period

increases, while the PACF is determined by assessing

the correlation between the sequence and the current

value after removing the influence of previous lag

periods.

The autocorrelation and partial autocorrelation

graphs are presented in Figures 3 and 4.

From Figure 3, it is evident that after two

differencing processes, the first lag period

significantly exceeds the significance threshold (blue

dashed line), followed by a gradual decrease in

subsequent lag periods. This suggests that the MA

component of the model may exhibit significant

autocorrelation with shorter lag periods. Generally

speaking, autocorrelation graphs quickly approach

zero after a lag period, usually indicating a low

q-value. In Figure 3, ACF demonstrates significant

autocorrelation at a lag period of 1, which

subsequently diminishes. Therefore, this study

determines the q value to be 1.

From Figure 4, the first lag period (Lag 1) exceeds

the significance threshold (blue dashed line) by a

significant margin. However, starting from the

second lag period, the PACF values quickly approach

zero, with no significant partial autocorrelation

observed. Given that only Lag 1 is significant and

subsequent lags contribute minimally to the model,

this study assumes a p-value of 1.

3.4 Model Fitting and Verification

Through the analysis of autocorrelation and partial

autocorrelation graphs, this study determined the

appropriate parameters for the ARIMA model. The

parameters of the model were determined to be based

on the characteristics of the secondary differential

processing and ACF and PACF graphs as p=1, d=2,

and q=1. Therefore, the final model is ARIMA (1, 2,

1).

This study fitted the ARIMA(1, 2, 1) model to the

data after second-order differencing. The estimated

results indicate that the AR(1) coefficient is 0.1248,

which is less than its standard error of 0.3078, and the

MA(1) coefficient is -0.7470, which exceeds its

standard error of 0.2613. This implies that the

autoregressive component of the model has a weaker

impact, whereas the moving average component

exhibits a more substantial influence.

To achieve more accurate and reliable model

fitting, residual testing is essential. In this study, the

Ljung-Box test was employed. According to the

Ljung-Box test, the X-squared value is 11.451, the

degrees of freedom is 20, and the p-value is 0.9337,

which exceeds 0.05. This indicates that the residuals

approximate white noise and there is no significant

autocorrelation in the residual sequence. Thus, it can

be concluded that the model does not omit critical

information. Furthermore, the autocorrelation plot of

the residuals shows that the first-lag autocorrelation

coefficient of the residuals is -0.0281, which is very

close to zero. This confirms that the residuals of the

model approximate white noise.

3.5 Predicting the Population for the

next Decade

Based on the established ARIMA(1, 2, 1) model, the

population of Zhengzhou City over the next ten years

was predicted, with the results presented in Table 2

9 )

According

the

point

prediction

population

values

Table 2: Population Growth Forecast of Zhengzhou City from 2023 to 2032 (Unit: ten thousand people)

Yea

Point forecast

ulation 80% confidence interval 95% confidence interval

2023 1304.748 1280.482 - 1329.015 1267.636 - 1341.861

2024 1328.363 1287.050 - 1369.676 1265.180 - 1391.546

2025 1352.186 1294.179 - 1410.193 1263.472 - 1440.900

2026 1376.035 1300.892 - 1451.178 1261.113 - 1490.956

2027 1399.887 1306.892 - 1492.881 1257.664 - 1542.109

2028 1423.739 1312.082 - 1535.396 1252.974 - 1594.504

2029 1447.591 1316.431 - 1578.751 1247.000 - 1648.183

2030 1471.444 1319.941 - 1622.947 1239.740 - 1703.147

2031 1495.296 1322.622 - 1667.970 1231.213 - 1759.379

2032 1519.148 1324.492 - 1713.805 1221.447 - 1816.850

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

values of the model, the population of Zhengzhou

City will steadily increase over the next decade.

The predicted values for each year in Table 2

include corresponding confidence intervals. The 95%

confidence interval provides a conservative estimate

for population forecasting, while the 80% confidence

interval offers a relatively compact and reasonable

prediction range to complement the uncertainty of the

forecast results.

According to the latest statistical bulletin issued

by the Zhengzhou Municipal Bureau of Statistics, the

actual permanent resident population in Zhengzhou

in 2023 was 13.008 million, while the

model-predicted value was 13.04748 million. The

absolute error between the two values is 0.03948

million, and the relative error is approximately 0.30%.

The actual value falls within the 95% confidence

interval of the predicted population, indicating that

the model's quantification of uncertainty is

reasonable. Due to the limited availability of

single-year data for 2023, the calculation and

interpretation of statistical indicators, such as mean

square error and coefficient of determination, are

constrained. In the future, multi-year data should be

integrated to further validate the reliability of the

model.

This study established an ARIMA (1,2,1) model

with a good fitting effect based on historical

population data from Zhengzhou. However,

population growth is influenced by various factors,

including urban construction, industrial development,

and public budget expenditures (Fang, 2021). This

study only considered historical population data for

Zhengzhou and did not incorporate external variables.

If there is a structural mutation in the data, it may not

be possible to capture the new trend after the

mutation point. Therefore, methods such as the

Bai-Perron test could be introduced to detect jumps

and mutations in time series by observing and

capturing them, enabling segmented modeling or the

introduction of dummy variables for improvement

(Zhu, 2024). The fitting and prediction performance

of the ARIMA model depends on parameter selection

through manual intervention, and its ability to process

nonlinear data is limited. Long-term prediction errors

may accumulate. In practical applications, the

ARIMA model is often combined with machine

learning models for compensation, such as stepwise

regression prediction, which can optimize the model

through data-driven methods and exhibits strong

flexibility and adaptability (Huang, 2025).

4 CONCLUSION

In recent years, Zhengzhou has experienced

significant population growth, primarily driven by

national policy support, geographical advantages,

industrial transformation and upgrading, and

economic development. This study employed time

series analysis methods and conducted rigorous

fitting analysis based on population data from the

Zhengzhou Bureau of Statistics spanning 1982 to

2022. An ARIMA (1,2,1) model with a good fitting

effect was constructed, predicting that Zhengzhou's

population will continue to maintain stable growth

over the next few years, with the resident population

expected to exceed 15 million by 2032. Based on the

results of this study, it can be inferred that

Zhengzhou's population growth trend will remain

relatively stable over the next decade, with promising

potential for continued growth. However, while the

model provides relatively reliable predictions, actual

population growth in Zhengzhou may still be

influenced by various factors. In the long term, with

the expansion of population size, limitations in

resource carrying capacity, as well as the impact of

economic fluctuations, industrial transformation,

regional competition, policy changes, and other

factors, the future long-term population growth in

Zhengzhou is fraught with challenges and

uncertainties. In future research, we can continue to

monitor the accuracy of the model and make

adjustments and revisions based on new data to

conduct in-depth analyses of Zhengzhou's future

population growth trends.

REFERENCES

Fei, J. 2024. Analysis of the fluctuation characteristics and

regional impact of RMB exchange rates on three

currencies: based on MSAR model and Bai-Perron test.

Chinese Business Theory, 15, 31-36.

Fang, W. L. 2021. Analysis of factors influencing the

growth of permanent resident population in Hangzhou

City. Statistical Science and Practice, 10, 29-32.

Feng, Y. J. 2024. Construction of the competitiveness

evaluation model and indicator system for Zhengzhou

national central city. China's Strategic Emerging

Industries, 30, 146-148.

Huang, Q. 2025. Analysis of crop yield prediction in

Qinghai Province based on stepwise regression and

ARIMA model. Southern Agricultural Machinery, 04,

173-176.

Jia, W. M. & Guo, X. M. 2025. Spatial heterogeneity

analysis and driving forces exploring of floating

population in China's central and western regions: a

Prediction of Urban Population Growth in Zhengzhou City Based on Time Series Analysis

case of Henan Province, China. Applied Geography,

176, 103516-103516.

Xi, J. 2020, November 2. Speech at the 7th national census

registration. People's Daily.

Zhang, K. G., Meng, H. L., Ba, M. T. & Wen, D. H. 2024.

The spatial distribution characteristics of resident

population growth rate in Henan Province, China.

Journal of Geoscience and Environment Protection,

11, 191-206.

Zhengzhou Daily. 2023. The relevant person in charge of

the Provincial Bureau of Statistics interpreted the

economic performance of the province from January to

April, and the gathering capacity of the Zhengzhou

metropolitan area has significantly improved.

Zhengzhou Municipal People's Government.

https://www.zhengzhou.gov.cn/news1/5013122.jhtml

Zhengzhou Municipal Bureau of Statistics. 2023. Annual

population. Zhengzhou Municipal Bureau of Statistics.

Zhengzhou Municipal Bureau of Statistics & Zhengzhou

Investigation Team of National Bureau of Statistics.

2024. Statistical bulletin on national economic and

social development of Zhengzhou City in 2023.

Zhengzhou Municipal Bureau of Statistics.

https://tjj.zhengzhou.gov.cn/tjgb/8324080.jhtml

Zou, H. 2024. Analysis of the phenomenon of population

return and economic development opportunities in the

central and western regions. China Economic and

Trade Journal, 18, 73-75.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy