Analysis of Influencing Factors of Medical Health Insurance Based

on the Multiple Linear Regression Method

Zihan Xu

Beijing Normal-Hong Kong Baptist University Faculty of Science and Technology Statistics,

Guang Dong, Zhu Hai, 519000, China

Keywords: Multiple Linear Regression, Medical and Health Insurance, Consumer Demand.

Abstract: With the rapid development of the insurance industry and people's increasing attention to health, the insurance

market has ushered in a good development space. However, the habits and needs of consumers directly affect

the medical and health insurance industry. Exploring the control of influencing factors of health insurance

can better allocate health care services to improve the efficiency of the health care system. Therefore, this

paper selects variables and data related to personal medical consumption from the Kaggle website, takes the

personal medical expenses charged by health insurance as the explanatory variable, and takes the age, gender,

BMI index, number of children raised by the insured, whether the insured has smoking habits, and region as

the explanatory variable to establish a multiple linear regression model and test it. The empirical results show

that the age of the insured, the BMI index, the number of children raised, and whether the insured smokes

have a significant impact on the personal medical expenses issued by the health insurance.

1 INTRODUCTION

Commercial insurance markets around the world are

developing at a high speed, and the total premium

income is growing continuously. Since 2020, its total

revenue has increased from US $3.96 trillion to US

$4.17 trillion, up 3.7% year on year (Guo, 2024). With

the rapid development of Internet finance-related

technologies, the income level of residents is

constantly improving, with higher requirements for

the quality of life, and people are paying more and

more attention to health issues. At present, the number

of people with various chronic diseases and sub-

health conditions has surged, and the number of

malignant tumors has increased. In addition to the

outbreak of the COVID-19 epidemic, the public's

demand for health insurance has become more urgent

(Chen et al., 2023). The total number of health

insurance products that consumers are willing to

purchase in a specific period and have the ability to

purchase is insurance demand (Feng, Xu, Zou, 2023).

Therefore, the customer demand of the health

insurance market is composed of the purchase

intention and actual purchasing ability of the

https://orcid.org/0009-0004-8897-7226

applicant. By improving the coverage of medical

insurance, medical and health services can be

efficiently used to control the medical and health costs

of patients, and medical insurance can also effectively

share the disease risk of residents (Qi, 2023).

Fulton et al. (2018) studied the health expenditure

in California, and the results showed that factors such

as population aging, per capita real income, and

medical industry inflation were closely related to the

increase in health expenditure. At the same time,

technological innovations such as risk-sharing

systems, value-based payments, and practice

adjustments could potentially constrain the growth of

health spending. The research on whether economic

incentives should be implemented in Australia's

health insurance shows that the target group of health

insurance is mainly high-income people (Kettlewell

& Zhang, 2024). There is a clear trend of financial

inequality in the insurance industry, and the reason

behind it is that the poor have far fewer opportunities

to purchase insurance for various risks than the rich

or the middle class (Tsvetkova et al., 2022).

Therefore, the level of income has become one of the

key research objects of the factors affecting medical

insurance. A study on the driver allocation of

Xu, Z.

Analysis of Inﬂuencing Factors of Medical Health Insurance Based on the Multiple Linear Regression Method.

DOI: 10.5220/0013813500004708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Innovations in Applied Mathematics, Physics, and Astronomy (IAMPA 2025), pages 31-36

ISBN: 978-989-758-774-0

commercial health insurance in China highlights the

current research on the impact of aging on insurance

purchase intention and believes that participation of

middle-aged and elderly people in health insurance

plans has a positive impact on their physical condition

(Huang et al., 2022). Bhawani analyzed its impact on

the health service industry from the aspects of

enterprise competition and the supply of production

factors and proposed to increase the financial support

for the industry and the guidance function of the

government to avoid vicious competition (Bhawani,

2010). Zhao & Li (2024) believe that consumers'

participation in commercial medical insurance is

mainly influenced by subjective factors such as

gender, job category, and economic status and

objective factors such as the management and

operation of insurance companies.

According to Davilla & Jones (2025), forward-

looking policies aimed at improving the efficiency of

healthcare systems through better control and

distribution of healthcare services require information

from the general population. Existing research has not

distinguished the impact of various factors on

insurance demand among different insured

individuals. This study established four linear

regression models and screened for the optimal

model, examining key factors and characteristics that

influence the insurance purchasing decisions of

insured individuals or their family members.

2 PRINCIPLES OF MULTIPLE

LINEAR REGRESSION AND

MODEL SELECTION

CRITERIA

The main principle of multiple linear regression is to

build a regression equation containing multiple

independent variables and a dependent variable and

interpret and infer the value of the dependent variable

according to the value of multiple independent

variables. Therefore, using the optimal set of multiple

independent variables to predict the dependent

variables is more accurate than using a single

independent variable to predict. The core of the

multiple linear regression model is to build a function

that can minimize the square value of the difference

between the predicted value and the true value. The

multiple linear regression model is usually used to

describe the random linear relationship between the

dependent variable 𝑌 and the independent variable

𝑋. The use of multiple linear regression also requires

the following three conditions: first, there must be a

random linear relationship between 𝑌 and 𝑋 .

Second, each observation value 𝑌 is independent of

each other. Third, the residual should be subject to the

normal distribution with the mean value of 0 and the

variance of 𝛿



, that is, for any group of observations

of the independent variable, the dependent variable 𝑌

has the same variance and is subject to the normal

distribution (Lu et al., 2025).

The purchase factor prediction model of medical

health insurance studied in this paper is aimed at a

regression problem, and the adjustment coefficient of

determination R²_adj, coefficient of prediction value

of determination R² _pred, root mean square error

Root Mean Square Error (RMSE), sum of prediction

error of Prediction Residual Error Sum of Squares

(PRESS), and Cp statistics are used to evaluate the

prediction model. The above evaluation indicators of

the original model and the new model were calculated

and compared one by one, and the optimal model was

finally selected (Qin, 2024).

Adjusted R-squared is an adjustment based on R-

squared, which is used to measure the degree of

interpretation of independent variables to dependent

variables. R-squared predict value is an indicator used

to measure the degree of fitting and prediction ability

of linear regression models to new data not used for

model training. In practical applications, their values

are usually between 0 and 1, and the closer to 1, the

better the model fits the data; The closer to 0, the

worse the fitting effect of the model. RMSE quantifies

the average error range of model prediction. The

smaller the value, the higher the prediction accuracy

of the model. PRESS value can evaluate the

generalization ability of the model and reflect the

prediction error of the model to new data. The smaller

the value, the stronger the prediction ability of the

model, and the lower the risk of overfitting. The Cp

value is used to measure the comprehensive impact of

model deviation and variance. The closer the number

of independent variables p is, the better the model will

be.

3 EMPIRICAL ANALYSIS

3.1 Data Collection and Processing

In view of the fact that this paper is going to study the

factors affecting medical and health insurance, this

paper collects and collates the statistical data set of

relevant factors affecting personal medical expenses

charged by health insurance from the Kaggle website

for empirical analysis. This data set is the first-hand

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

real data collected by Klymentiev (2018) from the

area where he lives on the Kaggle website, and more

than 60000 people have browsed and downloaded this

data before this. Therefore, this data set is reliable and

has research value. This data set contains 1338

samples and 7 variables, namely age, sex (male,

female), BMI, children, smoker, region, and charges.

After understanding the basic structure and

information of the data, the data set was cleaned, the

outliers and duplicate values were eliminated, and the

missing values were filled with average values. Then,

the data was converted into a format suitable for

analysis and standardized, and the data that could be

used for subsequent statistical analysis were obtained.

3.2 Basic Data Analysis

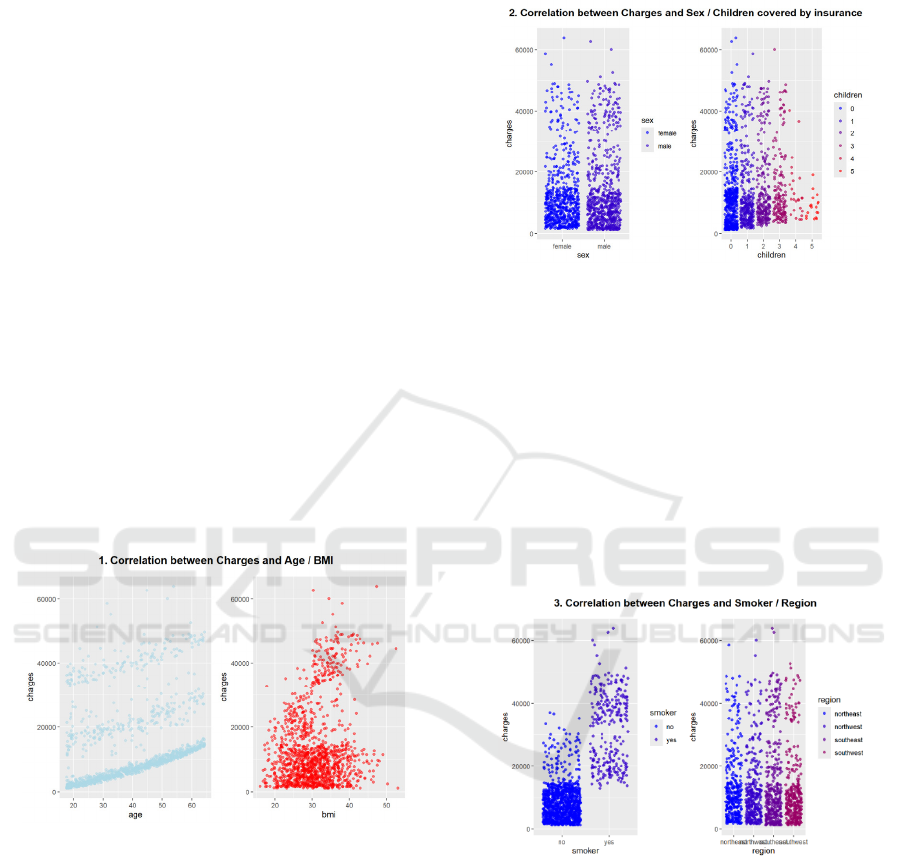
In this paper, scatter plots are drawn for six variables

in the data that affect the cost of health insurance. As

shown in Figure 1, the cost of health insurance

increases with the age of the insured and the increase

of the insured's body mass index. Moreover, in all age

groups and BMI ranges, the vast majority of people

who buy medical and health insurance spend less than

20,000, and the number of people who buy medical

and health insurance whose BMI is greater than 20

and less than 40 is large and concentrated.

Figure 1: Scatter plot of the relationship between Medicare

billing and the age and BMI of the policyholder

(Photo/Picture credit: Original).

The scatter plot in Figure 2 shows that the

distribution of costs for purchasing health insurance

is roughly similar for men and women. For both men

and women, most investments fall between 0 and

20,000, with the number of people decreasing as

investment increases. Therefore, the gender of the

insured does not seem to have a significant impact on

individual medical expenses. In contrast, the number

of children an insured person has is the opposite; as

shown in Figure 2, there is a positive correlation

between health insurance costs and the number of

children an insured person has, meaning the more

children they have, the higher their health insurance

expenses.

Figure 2: Scatter plot of the relationship between health

insurance billing and the gender of the insured and the

number of children raised (Photo/Picture credit: Original).

Similarly, Figure 3 shows that whether or not an

insured person smokes has a significant impact on

personal health care costs - smokers pay significantly

more for health insurance than non-smokers. Similar

to the gender variable, the distribution of health

insurance investment in the northeast, northwest,

southeast, and southwest are identical, including the

growth trend, so the region where the insured lives

does not have a significant impact on health insurance

costs.

Figure 3: Scatter plot of the relationship between health

insurance billing and whether the insured person smokes

and where they live (Photo/Picture credit: Original).

3.3 Model Construction

According to the selected data, this paper takes the

personal medical expenses charged by the health

insurance as the explanatory variables, and takes the

age, gender, BMI - body mass index of the applicant,

that is, the ratio of height to weight, the number of

children covered by the health insurance, that is, the

number of children supported by the applicant,

whether the applicant smokes, and the residential area

Analysis of Inﬂuencing Factors of Medical Health Insurance Based on the Multiple Linear Regression Method

of the applicant as the explanatory variables.

Therefore, 𝑌𝑖 represents the personal medical

expenses issued by the health insurance,

𝑋1 represents the age of the applicant 𝑋2 represents

the gender of the applicant, 𝑋3 represents the BMI

of the applicant, 𝑋4 represents the number of

children covered by health insurance, 𝑋5 represents

whether the applicant smokes, and 𝑋6 represents the

residential area of the applicant. Therefore, set the

original model:

𝑌𝑖 = 𝛽0 + 𝛽1 𝑋1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 + 𝛽4 𝑋4 +

𝛽5 𝑋5 + 𝛽6 𝑋6 + εi (1)

Where the random error term 𝜀𝑖 is a random

variable that follows a normal distribution.

Table 1: Regression coefficient of the original model

Estimate Std.Erro

T value Signif. codes

(Intercept) -12269.71 1251.90 -9.80 ***

X1 263.84 14.99 17.60 ***

X2male -53.05 414.01 -0.12

X3 353.03 35.69 9.89 ***

X4 343.54 169.46 2.02 *

X5yes 23350.20 527.93 44.22 ***

X6northwest -574.30 590.85 -0.97

X6southeast -817.24 595.69 -1.37

X6southwest -1441.10 593.34 -2.42 *

Then, this paper conducts linear regression

analysis on the original model (Model_0) and obtains

the regression coefficient as shown in Table 1.

Estimate represents the estimated regression

coefficient of each variable. In the table, except for

the intercept, only the variables representing gender

and region are negative, which means that the average

change of the insured's gender and region is opposite

to the average change of the dependent variable -

personal medical expenses. According to Figure 2 and

Figure 3 in the basic data analysis and the linear

regression analysis of the original model as shown in

Table 1, individual variables are not important, such

as the gender and the region of the insured. Therefore,

on the basis of the original model, the variable 𝑋6

representing the insured area is deleted, and model I

is established:

𝑌𝑖 = 𝛽0 + 𝛽1 𝑋1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 + 𝛽4 𝑋4 +

𝛽5 𝑋5 (2)

Delete the variable 𝑋2 representing the gender of

the insured and establish model II:

𝑌𝑖 = 𝛽0 + 𝛽1 𝑋1 + 𝛽3 𝑋3 + 𝛽4 𝑋4 + 𝛽5 𝑋5 +

𝛽6 𝑋6 (3)

At the same time, delete the variable 𝑋2

representing the gender of the applicant and the

variable 𝑋6 representing the region of the applicant,

and establish model Ⅲ:

𝑌𝑖 = 𝛽0 + 𝛽1 𝑋1 + 𝛽3 𝑋3 + 𝛽4 𝑋4 + 𝛽5 𝑋5(4)

3.4 Screening and Determination of

Regression Models

Table 2: Comparison of four model indicators

Prediction result R²-adj R²_pre

RMSE PRESS Cp

Model_0 0.7341 0.7808 5848.0110 34845147347

—

Model

Ⅰ 0.7301 0.7820 5831.7990 34768109782 2.9577

Model

Ⅱ 0.7326 0.7807 5848.5640 34845548436 6.9868

Model

Ⅲ 0.7342 0.7821 5831.3000 34767737117 3.9467

It can be seen from Table 2 that the RMSE value

of model Ⅲ is smaller, indicating that the average

difference between the predicted value of the model

and the actual observed value is smaller, which means

that the prediction effect of the model is better, the

degree of data fitting is higher, and the rule in the data

can be more accurately captured and predicted.

Table 3: Three regression coefficients of the model

Estimate Std.Error

value

Signif.

codes

(Interce

)

-12749.12 1189.57 -10.71 ***

X1 264.40 15.00 17.62 ***

X3 343.94 34.57 9.95 ***

X4 333.84 169.47 1.97 *

es 23374.05 523.77 44.62 ***

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy

By observing Table 3, it can be concluded that the

estimations of regression coefficients in model Ⅲ

are all greater than 0 except for the intercept, and it

can also be intuitively observed through the

significance code that the four variables in model Ⅲ

have significant impacts on 𝑌𝑖 . In summary, this

paper chooses model Ⅲ:

𝑦



= 12749.17 + 264.40𝑋



+ 343.94𝑋



333.84𝑋



+ 23374.05𝑋



(5)

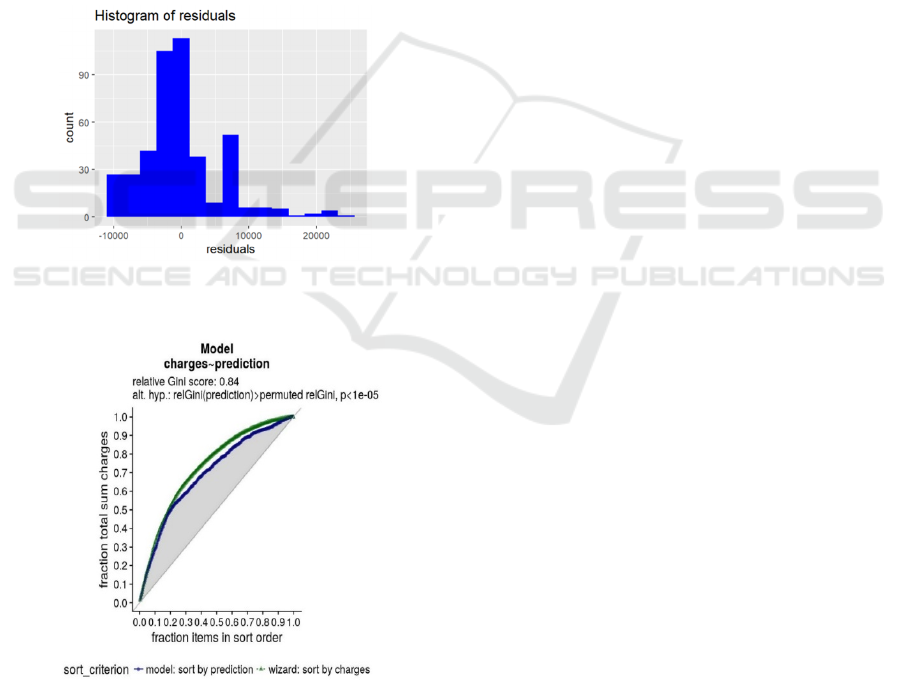
3.5 Residual Analysis

Figure 4 The distribution of the residual histogram is

roughly high in the middle and low on both sides. The

number of residuals near 0 is the largest, and the

number on both sides gradually decreases, which is

similar to the characteristics of normal distribution.

Figure 4: Histogram of residual error (Photo/Picture credit:

Original).

Figure 5: Model performance graph of the proportion of

total costs versus the proportion of items in order of ranking

(Photo/Picture credit: Original).

Figure 5 shows that the performance of the model

in Gini score = 0.84, an indicator to measure the

differentiation ability of the model, which indicates

that the model selected in this paper has a strong

ability to distinguish different categories or values. In

addition, the relative Gini score of the predictor is

significantly higher than that after replacement, and

the P-value is less than 0.00001, indicating a very

high level of significance. The two curves showing

the relationship between the proportion of the total

cost and the proportion of the items in order are close

and far away from the diagonal line. In addition, the

model error is close to zero, indicating that the model

has a good performance in predicting the cost, which

further indicates that the model has statistical

significance.

4 CONCLUSION

To sum up, this study systematically analyzed the key

factors affecting personal medical and health

insurance expenses through the multiple linear

regression method, built four prediction models based

on the Kaggle dataset, and conducted comprehensive

verification. Through a large number of calculations

and comparisons, this paper finally determined that

Model 3 was the optimal model among the four

candidate models, and its adjusted R ² reached

0.7342, and the predicted R² was 0.7821, indicating

that the model has good explanatory power and

prediction accuracy. In addition, residual analysis

shows that the error term of the model is

approximately a normal distribution, and the model

has excellent discrimination ability. Therefore, this

paper can determine that the age of the insured, its

BMI index, the number of children raised and whether

there is smoking habit are the main factors affecting

the personal medical expenses issued by the health

insurance, and these four variables are positively

correlated with the dependent variables, of which the

influence of smoking habit is the most prominent. It

is worth emphasizing that, different from the existing

research conclusions, this study finds that gender and

regional factors have no significant impact on health

insurance costs, which may reflect the specific

medical pricing policies or cultural factors in the

sample region.

REFERENCES

Bhawani, X. 2010. The determination of agglomeration in

health care sector employment in US metropolitan

areas. Paper Presented on 41st Annual and Conference

Analysis of Inﬂuencing Factors of Medical Health Insurance Based on the Multiple Linear Regression Method

Mid-Continent Regional Science Association, 12(7), 1-

23.

Chen, S., Lin, Z., Wang, X., & Xu, X. 2023. Pandemic and

insurance purchase: How do people respond to

unprecedented risk and uncertainty. China Economic

Review, 79, 61-62.

Feng, J., Xu, X., & Zou, H. 2023. Risk communication

clarity and insurance demand: The case of the COVID-

19 pandemic. Journal of Economic Dynamics and

Control, 146, 3-32.

Fulton, B., Scheffler, R., Keolanui, B., & Shortell, S. 2018.

Forecasts and drivers of health expenditure growth in

California. California Journal of Politics & Policy,

7(2), 177-178.

Guo, W. 2024. Income volatility and household commercial

insurance allocation. Finance Research Letters, 66, 5-

Huang, X., Tung, C., Wang, X., Xu, X., Lam, F., & Zhang,

T. 2022. Configurations of the driving factors

promoting China's commercial health insurance: A

comparative qualitative analysis based on the

Technology – Organization – Environment framework.

Heliyon, 8(11), 6-35.

Kettlewell, N., & Zhang, Y. 2024. Financial incentives and

private health insurance demand on the extensive and

intensive margins. Journal of Health Economics, 94, 2-

14.

Klymentiev, R. 2018. Health care cost prediction with linear

regression models.

https://www.kaggle.com/code/ruslankl/health-care-

cost-prediction-w-linear-regression/report

Lu, X., Teh, S., Tay, C., Kassim, N., Fam, P., & Soewono,

E. 2025. Application of multiple linear regression

model and long short-term memory with compartmental

model to forecast dengue cases in Selangor, Malaysia

based on climate variables. Infectious Disease

Modelling, 10(1), 240-256.

Qi, B. 2023. Property insurance company short-term

medical health insurance marketing strategy

optimization research. Master's thesis, Guizhou

University of Finance and Economics.

Qin, Y. 2024. A comparative study of housing price

forecasting models based on multiple linear regression

and random forest algorithm. Modern Information

Technology, 8(22), 127-131.

Tsvetkova, L., Okhrimenko, I., Belousova, T., &

Khuzhamov, L. 2022. Relationship and mutual

influence between poverty and insurance in a

developing insurance market. Journal of Behavioral

and Experimental Finance, 36, 66-67.

Zhao, J., & Li, F. 2024. Analysis of factors influencing

participation intention of inclusive commercial medical

insurance: Based on logistic regression and CHAID

decision tree model. Chinese Health Service

Management, 41(05), 523-528.

IAMPA 2025 - The International Conference on Innovations in Applied Mathematics, Physics, and Astronomy