NAMOUnc: Navigation Among Movable Obstacles with Decision
Making on Uncertainty Interval
Kai Zhang
1,2,3 a
, Eric Lucet
1 b
, Julien Alexandre Dit Sandretto
2 c
,
Shoubin Chen
3,∗ d
and David Filliat
2 e
1
Paris-Saclay University, CEA, List, 91120 Palaiseau, France
2
U2IS, ENSTA Paris, Institut Polytechnique de Paris, 91120 Palaiseau, France
3
Guangdong Laboratory of Artificial Intelligence and Digital Economy(SZ), 51800 Shenzhen, China
Keywords:
Navigation Among Movable Obstacles, Planning Under Uncertainty, Decision Making.
Abstract:
Navigation among movable obstacles (NAMO) is a critical task in robotics, often challenged by real-world un-
certainties such as observation noise, model approximations, action failures, and partial observability. Existing
solutions frequently assume ideal conditions, leading to suboptimal or risky decisions. This paper introduces
NAMOUnc, a novel framework designed to address these uncertainties by integrating them into the decision-
making process. We first estimate them and compare the corresponding time cost intervals for removing and
bypassing obstacles, optimizing both the success rate and time efficiency, ensuring safer and more efficient
navigation. We validate our method through extensive simulations and real-world experiments, demonstrat-
ing significant improvements over existing NAMO frameworks. More details can be found in our website:
https://kai-zhang-er.github.io/namo-uncertainty/.
1 INTRODUCTION
In real applications, robots take actions with par-
tial and noisy observation on the environment, and a
given action may cause unexpected effect due to un-
certainties. If the robot has over confidence on the
observation and action, it can lead to some subop-
timal decisions, even to dangerous actions resulting
in catastrophic effects, like destroying objects in the
workspace. It is therefore essential for the robot to
recognize the limitation of its observations and ac-
tions, and make decisions with awareness of uncer-
tainty and risks.
Recent studies on task and motion planning in-
corporate uncertainty and update plans based on the
observation and action uncertainties. For exam-
ple (Safronov et al., 2020; Pan et al., 2022) take suc-
cess rate (SR) into account in a manipulation task: if
a grasp action fails, the planner updates its estima-
a
https://orcid.org/0000-0003-1129-9944
b
https://orcid.org/0000-0002-9702-3473
c
https://orcid.org/0000-0002-6185-2480
d
https://orcid.org/0000-0002-9071-0051
e
https://orcid.org/0000-0002-5739-1618
∗
Corresponding author.
tion on SR, then replans for an action sequence with
a higher predicted SR. Methods such as probabilistic
symbolic planning (Silver et al., 2021) or Bayes op-
timization (Curtis et al., 2024) plan with uncertainty
but mainly focus on optimizing SR. They often ne-
glect joint optimization with efficiency, which is cru-
cial for navigation tasks.
Navigation among movable obstacles (NAMO)
task is mainly a navigation task but the robot is able
to manipulate movable obstacles (MO). Many exist-
ing solutions (Muguira-Iturralde et al., 2023; Ellis
et al., 2022) consider NAMO as a manipulation task,
assuming manipulation is necessary to complete the
task. However, the most common case is that the task
can be finished without moving the MO, by making a
detour. This oversight makes probability-based opti-
mization less useful, as bypassing with a SR close to 1
will be preferred even if it requires significantly more
time. Furthermore, in partial observation condition,
the invisible region in NAMO tasks is considerably
larger than in manipulation tasks. Common strategies
for reducing uncertainty in manipulation tasks, such
as exploring all occluded regions (Curtis et al., 2024),
are often inefficient or impractical for NAMO tasks
due to the scene complexity and large scale.
Zhang, K., Lucet, E., Sandretto, J. A. D., Chen, S. and Filliat, D.
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval.
DOI: 10.5220/0013806300003982
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 139-149
ISBN: 978-989-758-770-2; ISSN: 2184-2809
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
139

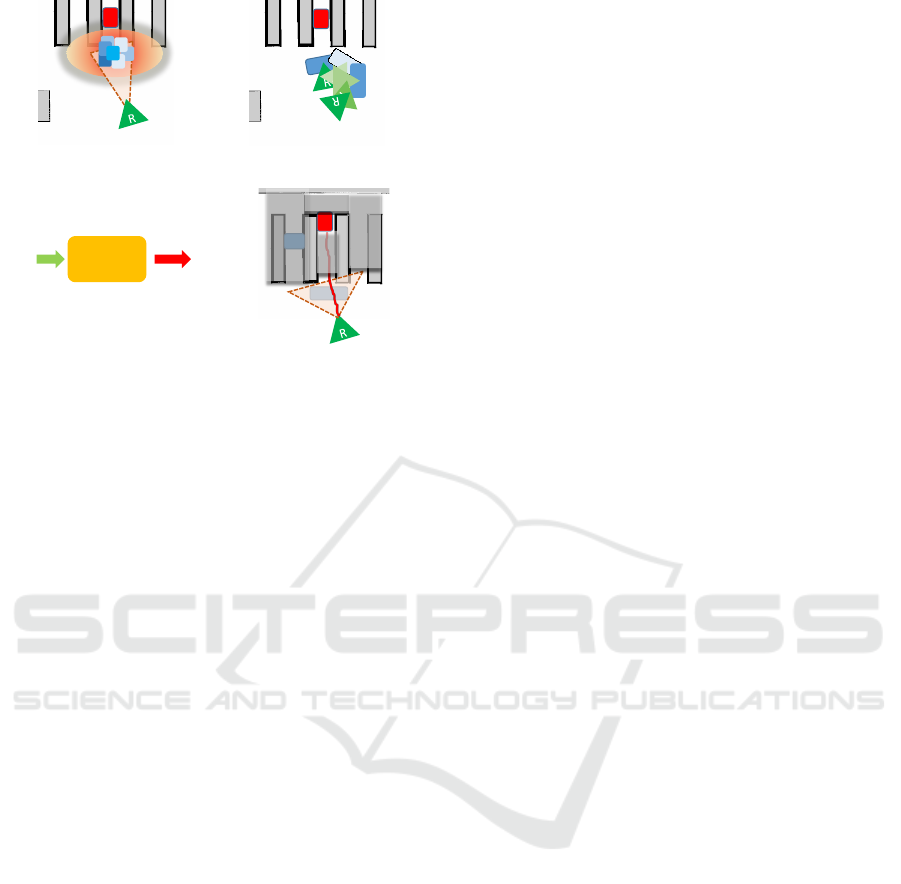
Model
𝑋
𝑦 ± 𝜎
(c) Model uncertainty
G
MO
(d) PO uncertainty
R
(a) Observation uncertainty (b) Action uncertainty
G
G
Figure 1: Primary sources of uncertainty in a NAMO
task.The illustration highlights four key uncertainties en-
countered during task execution. The blue rectangle rep-
resents the MO while the green triangle with R denotes the
robot. The red square labeled G indicates the goal. In sub-
figure (c), X denotes the observation while y and σ repre-
sent the prediction result and the corresponding prediction
uncertainty, respectively.
This paper presents NAMOUnc, a method for
solving NAMO tasks by optimizing both SR and goal
reaching time in real scenarios. Our main contribution
lies in enhancing the robustness of the NAMO method
with respect to the following uncertainties (Fig. 1):
(a) observation uncertainty on MO pose estimation
caused by sensor noise, (b) model approximation un-
certainty, (c) action uncertainty from imperfect con-
trollers, and (d) blockage uncertainty from partial ob-
servation. NAMOUnc estimates these uncertainties
as cost intervals and makes decisions based on their
utility values, balancing removal and bypass strate-
gies to achieve efficient and successful navigation.
In summary, our contribution includes:
1. A novel approach for solving NAMO tasks, opti-
mizing SR and efficiency under condition of par-
tial observability.
2. Four modules to systematically estimate and
quantify the uncertainties described in Fig. 1.
3. A novel method to estimate the uncertainty
caused by partial observation in unexplored re-
gion, which can effectively reduce the navigation
risk and improve the efficiency.
4. Experiments in simulated and real environments
to demonstrate the effectiveness of our method.
2 RELATED WORK
2.1 Navigation Among Movable
Obstacles
The NAMO task has been extensively studied, with
recent advancements focusing on end-to-end learn-
ing (Li et al., 2020) and hybrid approaches (Muguira-
Iturralde et al., 2023; Kim et al., 2019; Xia et al.,
2021). End-to-end learning methods typically em-
ploy hierarchical reinforcement learning (Li et al.,
2020), generating high-level subgoals alongside low-
level control parameters. Hybrid methods, on the
other hand, leverage machine learning either to pro-
duce subgoals (Xia et al., 2021) or to assist in generat-
ing action sequences (Muguira-Iturralde et al., 2023).
A comprehensive review of these techniques is pro-
vided in (Zhang et al., 2022).
Existing methods primarily focus on task comple-
tion without considering the associated costs. A re-
lated work (Zhang et al., 2023) introduced a strategy
selection mechanism based on estimated costs, jointly
optimizing SR and efficiency. However, this approach
does not incorporate uncertainty, which limits its gen-
eralizability and applicability in real-world scenarios.
Therefore, we propose NAMOUnc method in this pa-
per as an extension to deal with real-world cases.
2.2 Planning with Uncertainty
Uncertainty in real-world environments introduces
significant challenges, prompting the development of
methods to address various types of uncertainties, in-
cluding observation uncertainty, action uncertainty,
and uncertainty arising from partial observability.
Observation uncertainty in task planning pertains
to the confidence in object classification and pose es-
timation. Object classification uncertainty has been
extensively studied in computer vision (Feng et al.,
2021), with confidence scores commonly used to
quantify this uncertainty. Pose uncertainty, often re-
sulting from sensor noise, is often modeled as a Gaus-
sian distribution and mitigated through repeated ob-
servations (Kaelbling and Lozano-P
´
erez, 2013; Gar-
rett et al., 2020).
Action uncertainty has garnered increasing atten-
tion. In sampling-based methods, action uncertainty
is represented as a probabilistic transition matrix,
which can be approximated through frequent replan-
ning (Garrett et al., 2020) or learned from demonstra-
tions and datasets (Silver et al., 2021). This matrix
enables the selection and execution of the most likely
successful plan. Rather than treating it as an open-
loop process, some approaches (Pan et al., 2022) it-
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
140

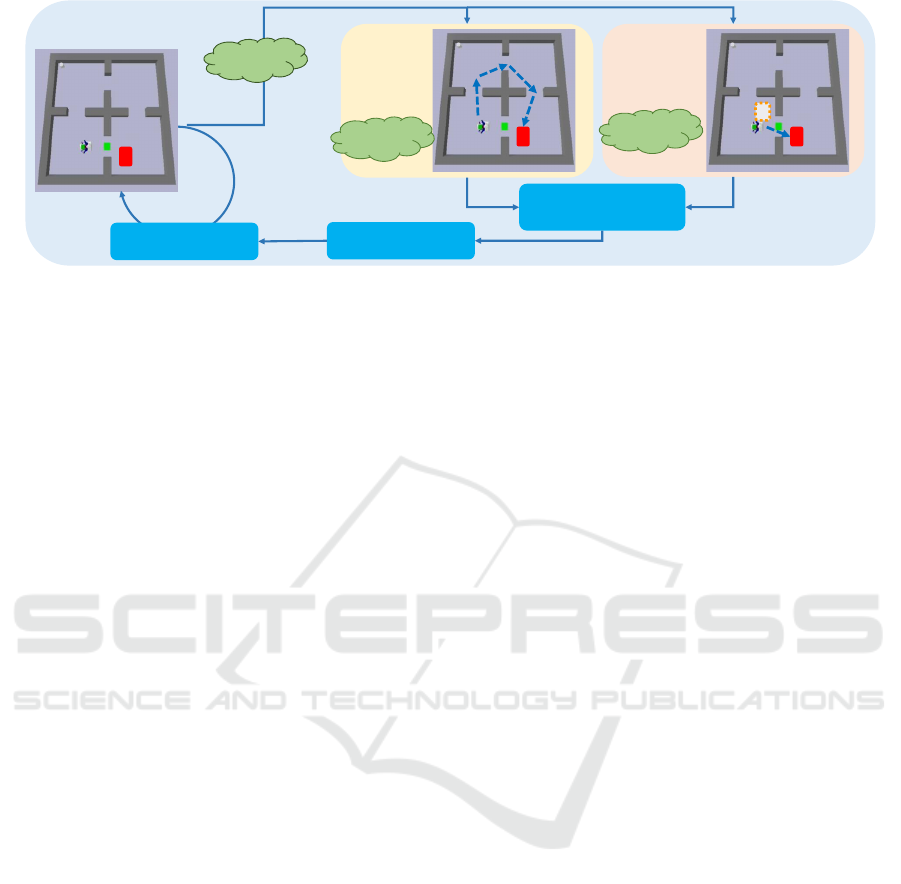
Decision making in
belief space
Detected MOs
Bypass or removal
Calculate
bypass cost
𝐶
𝑏𝑦
Estimate
removal cost
𝐶
𝑟𝑒
G
G
G
(a)
(b)(d)
(b)(c)(d)
Plan execution
Motion planning
Figure 2: Overview of the NAMO method pipeline. When being blocked by MOs during navigation, the robot estimates
the bypass and removal cost to choose an efficient strategy to continue its task. The green cloud symbols represent the
uncertainties associated with each module: (a) Observation uncertainty; (b) Model uncertainty; (c) Action uncertainty; (d)
Blockage uncertainty caused by partial observability.
eratively update transition probabilities based on ob-
served action effects, dynamically adjusting plans to
achieve task objectives.
Regarding uncertainty from partial observation,
most methods (Muguira-Iturralde et al., 2023; Cur-
tis et al., 2024; Wu et al., 2010) restrict actions to the
sensor’s field of view. In manipulation tasks, stud-
ies such as (Curtis et al., 2024; Garrett et al., 2020)
model the probability of unseen objects behind visible
ones, incorporating this into planning to trigger ex-
ploration actions when necessary. For NAMO tasks,
RNAMO (Wu et al., 2010) proposes pushing all ob-
stacles in invisible regions; if obstacles are immov-
able, the robot updates its internal map and plans a de-
tour. In larger workspaces, LaMB (Muguira-Iturralde
et al., 2023) employs backward reasoning to elimi-
nate environmental invisibility, though this approach
is limited to small environments due to its exhaustive
exploration of invisible regions. To address this limi-
tation, we introduce a method to quantify the potential
cost of navigating through unexplored areas, optimiz-
ing the trade-off between exploration (bypassing into
unknown regions) and exploitation (manipulating vis-
ible obstacles).
3 NAVIGATION AMONG
MOVABLE OBSTACLES WITH
UNCERTAINTY
In a NAMO task, shown in Fig. 2, a robot needs to
navigate to a goal while avoiding obstacles. With
the environment map, the first step is to plan and fol-
low the shortest path. If meeting a MO blocking this
path, the robot can choose to bypass it or clear the
path by removing it. As described in our previous
work (Zhang et al., 2023), we first estimates the by-
pass and removal cost before making decision. The
bypass cost is calculated based on a detour trajectory
while the removal cost is computed in two steps: pre-
dicting the stock region for the MO, then estimating
the time of moving the MO to this region. The mo-
tion planner outputs control parameters for the robot
to follow the best alternative.
Uncertainties across different system components
can significantly affect task success. In the context
of MO detection and localization, observation-related
uncertainties, such as recognition errors and pose es-
timation inaccuracies, can lead to collisions or unsuc-
cessful removal attempts. Similarly, model uncertain-
ties in estimating the costs of bypassing or remov-
ing obstacles may yield inaccurate evaluations. If the
robot opts to remove a MO, the action may fail due to
incomplete knowledge or discrepancies between the
predicted and actual outcomes of the action. Further-
more, operating in partially observable environments
introduces intrinsic uncertainty, which often results
in a divergence between anticipated and actual con-
ditions.
To quantify the impact of these uncertainties on
the decision-making process, we use time intervals,
denoted as [ ], which reflect the range of potential
outcomes generated by uncertainty, before selecting
the best option based on their utility values. In the
following section, we present the methods of quanti-
fying these uncertainties using intervals.
4 UNCERTAINTY ESTIMATION
METHOD
We now present four uncertainties considered in
NAMO tasks and the methods to estimate them, be-
fore detailing the decision process.
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval
141

4.1 Observation Uncertainty
While navigating the environment, the robot should
localize MOs and detect whether the planned path is
blocked. Due to the sensors’ noise in object detec-
tion and localization error of the robot, the estimated
MO pose is subject to uncertainty. However, multiple
observations can refine the result, and given a spec-
ified confidence interval, a belief region representing
the MO’s position can be calculated for path blockage
determination.
The obstacle pose is computed from the robot pose
plus the relative pose of the MO given by the sen-
sor. Assuming the robot pose from the localization
algorithm is X
r
= (x
r
,y
r
,θ
r
) with covariance Σ
r
, and
the relative distance and angle of the i-th MO mea-
sured by the depth camera Y
i
= (d
i
,φ
i
) with covari-
ance Σ
Y
, the obstacle pose X
i
MO
can be obtained by:
X
i
MO
= (x
r
+ d
i
cos(θ
r
+ φ
i
),y
r
+ d
i
sin(θ
r
+ φ
i
))
T
and
the covariance matrix Σ
MO
by:
Σ
i
MO
= J
r
Σ
r
J
T
r
+ J
y
Σ
Y
J
T
y
; J
r
=
∂X
i
MO
∂X
r
; J
y
=
∂X
i
MO
∂Y
i
(1)
When multiple observations of the same MO are
received, a Kalman filter (Kalman, 1960) is applied
to fuse the repeated observations and obtain the esti-
mated MO pose and its covariance.
Given a confidence score T
con f
, set to 95% in our
experiments, though other values are possible, the be-
lief region of the MO pose is represented as an ellipse
computed from the covariance matrix. We add the
size of the MO, expressed as its radius, to obtain the
ellipse region where a path would lead to potential
collision. In this case, the robot stops and chooses the
best strategy as described in Sec. 4.5.
4.2 Bypass Cost Model Uncertainty
The bypass cost, defined as the estimated travel time
to reach the goal when the robot follows a planned
detour, varies depending on the trajectory and the
robot’s moving speed. A deterministic predictor of
navigation time inherently involves uncertainty, since
in practice the robot may deviate from the planned
trajectory. To capture this prediction uncertainty, we
express the estimated time as an interval rather than a
single value.
To plan the detour, a MO and its uncertainty re-
gion (an ellipse with 95% confidence as described in
Sec. 4.1) is temporarily added to the obstacle map,
then the shortest path planner searches a path to by-
pass the MO. If no path is found, the bypass time cost
is set to C
by
nav
= In f . On the contrary, if a path is found,
we need to estimate the navigation time from trajec-
tory features. While the average speed was simply
used in (Zhang et al., 2023), we use a Gaussian lin-
ear regressor (GLR) (Williams and Rasmussen, 1995)
for better prediction and uncertainty evaluation (see
Sec. 5.3).
In practice, as rotation takes more time than fol-
lowing straight lines, we need to take the orientation
change of the trajectory into account during bypass
time estimation. In addition to the trajectory length
F
l
, we therefore calculate the trajectory smoothness F
s
and variance of direction change F
v
as features to esti-
mate the navigation time. Assuming a trajectory con-
sists of N waypoints pt
i
,i = 0,1,..,N, each pt
i
charac-
terized by position p
i
and orientation α
i
, smoothness
and variance are calculated using:
F
s
=
∑
N
i=1
|α
i
− α
i−1
|
N − 1
;F
v
= var(|α
i
− α
i−1
|) (2)
A trajectory is therefore characterized by X =
{F
l
,F
s
,F
v
}. Then, the bypass time cost and variance
are predicted by a GLR:
T
by
,σ
by
= GLR(X) (3)
The navigation time interval with T
con f
= 95% confi-
dence is: [C
by
nav
] = [T
by
− 2σ
by
,T
by
+ 2σ
by
].
To train the regression model, we collect a set of
trajectories by controlling the robot to navigate in a
warehouse environment. The pose and time stamp
are recorded along these trajectories, and we create
a large and varied dataset for the model by sampling
random start and goal points in these trajectories and
computing the corresponding features and duration.
4.3 Removal Action Uncertainty
The action uncertainty relates to the uncertain out-
come of loading a MO for displacement, which can
be either success or failure.
For a given SR, p
a
, the expected removal cost C
MO
is
C
MO
= T
MO
M
∑
i=1
ip
a
(1 − p
a
)
i−1
+
(MT
MO
+C
by
)(1 − p
a
)
M
(4)
where M defines the maximum attempts when the
robot continuously fails to load a MO (according to
the psychological view on learned helpless (Maier
and Seligman, 1976)). C
by
denotes the obstacle by-
pass cost, and T
MO
is the removal cost of a MO that
can be estimated by the method proposed in (Zhang
et al., 2023), where a stock region predictor and a re-
gression model are employed to predict the placing
pose and the removal time.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
142

In practice, the SR may not be fixed and can
evolve during robot operation, we therefore start by
an initial estimate and update it after each trial. Sim-
ilar to (Curtis et al., 2024), we model the SR of an
action and the uncertainty of its estimation after t tri-
als, p
t
a
, using a Beta distribution. To obtain the ini-
tial SR, p
0
a
, we control the robot to load the MO in
several trials (10 in our experiments) and record the
action results. Assuming there are α successful trials
and β failure cases, the initial knowledge on the trial
results can be described as p
0
a
∼ Beta(α, β). During
operation, when new trials are performed, the updated
posterior is p
t
a
∼ Beta(α +s,β + f ) where s and f are
the number of successful and failed object manipula-
tion respectively. With a confidence score T
con f
, we
can obtain the SR interval:
p
t
a
∈ [Beta.pp f (
1 − T
con f
2
),Beta.pp f (
1 + T
con f
2
)]
(5)
where the Beta.pp f is the point percent function to
obtain the confidence interval of the beta distribution
given a confidence score.
We compute the interval of the expected removal
cost [C
MO
] by using Eq. 4 with the minimum and max-
imum p
t
a
of the SR interval.
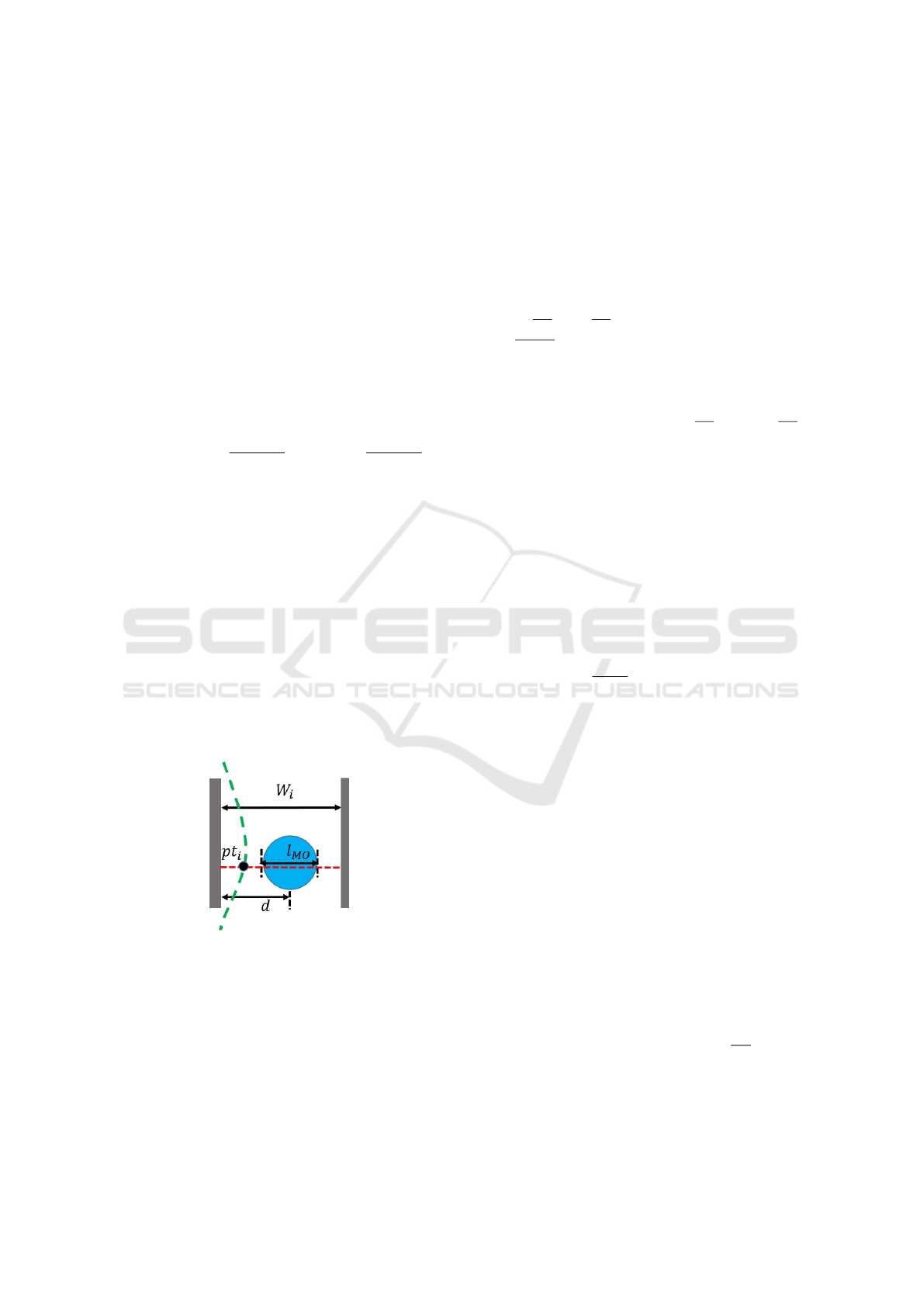
4.4 Blockage Uncertainty
Blockage uncertainty comes from the partial observa-
tion condition and results in a blocking probability of
the robot by some unseen MOs in unexplored region.
It is related to the passage width and robot size as it
is more risky if the planned navigation path passes a
narrow passage rather than an open space.
Figure 3: Blocking case. The blue circle represents the MO
in a corridor with width W
i
. The green dash curve is the
planned trajectory of the robot while the red dash line is the
traversal line at waypoint pt
i
.
To calculate the blockage probability of a trajec-
tory T , we take T as a set of way points pt
i
,i =
1,2, ...,N and compute the blockage probability of
each way point.
We model the blockage probability based on sev-
eral assumptions (shown in Fig. 3):
(i) The width of the passage W
i
at pt
i
,
(ii) The radius of the robot r,
(iii) The diameter of the MO, l
MO
, modeled as a
Gaussian distribution G(µ,σ) where µ is the av-
erage radius of the MOs and σ is the standard
deviation.
(iv) The distance between the MO center and the
wall d, modeled as a uniform distribution d ∼
U(
l
MO
2
,W
i
−
l
MO
2
), which leads to p(d|l
MO
,W
i
) =
1
W
i
−l
MO
.
Given d, l
MO
, r and W
i
, the blockage probability
is deterministic: p(b|d,l
MO
,W
i
,r) = 1 when the size
of robot is larger than the space of both sides of the
MO, represented by 2r > max(d −
l
MO
2
,W
i
−d −
l
MO
2
);
otherwise, p(b|d,l
MO
,W
i
,r) = 0.
To obtain the blockage probability conditioned
only on the passage width and the robot size
p(b|W
i
,r), we first eliminate the dependence on d
through marginalization:
p(b|l
MO
,W
i
,r) =
Z
W
i
−l
MO
/2
l
MO
/2
p(b|d,l
MO
,W
i
,r)p(d|l
MO
,W
i
,r)d
d
(6)
After simplification, we get:
p(b|l
MO
,W
i
,r) =









0, l
MO
< W
i
− 4r
4r
W
i
−l
MO
− 1, W
i
− 4r < l
MO
< W
i
− 2r
1, W
i
− 2r < l
MO
< W
i
0, W
i
< l
MO
(7)
The blockage probability in a corridor is then:
p(b|W
i
,r) =
Z
p(b|l
MO
,W
i
,r)p(l
MO
)d
l
MO
(8)
Considering that l
MO
satisfies a Gaussian distribu-
tion and p(b|l
MO
,W
i
,r) is piecewise constant, we ap-
proximate this integral by using a sampling method.
The previous p(b|W
i
,r) is calculated with the as-
sumption of a MO being on the line perpendicular to
the corridor passing through pt
i
(the red dash line in
Fig. 3). Because W
i
can be obtained from pt
i
using
a ray casting algorithm, and both are independent of
r, the blocking probability at pt
i
can be expressed as
p(b|pt
i
,r) = p(b|W
i
,r).
Assuming the MO is uniformly distributed in the
space with a free area A, the probability that the MO
is in the traversal line at pt
i
is p(pt
i
) =
W
i
K
A
. Here K
is a parameter characterising the obstacle appearance
probability. It’s worth noting that the assumption on
uniform distribution is based on the absence of prior
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval
143

knowledge about the object organization in the envi-
ronment. However, if prior information is available,
the distribution should be adjusted accordingly.
Therefore, the probability that the robot is blocked
at pt
i
is p(b|pt
i
,r) × p(pt
i
). Then, for a trajectory T ,
the blockage probability p(b|T,r) can be computed
by:
p(b|T,r) = 1 −
T
∏
pt
i
(1 − p(b|pt
i
,r) × p(pt
i
)) (9)
The estimated cost of blockage when passing the
invisible region is then :
[C
blocked
] = p(b|T,r) × [C
MO
] (10)
4.5 Decision Making with Uncertainty
Interval
The decision-making module aims to compare the
costs of bypassing and removal, then to choose the
one with the lower cost.
With the uncertainties considered, the final cost of
each option can be calculated by
[C
by
] = [C
by
nav
] + [C
by
blocked
] (11)
[C
re
] = [C
MO
] + [C
re
nav
] + [C
re
blocked
] (12)
where [C
by
blocked
] and [C
re
blocked
] are the blockage costs
of bypass and removal trajectories.
For the decision making between the cost inter-
vals, we apply the Laplace criterion, described in (De-
noeux, 2019), to compute the average utility of the
consequences of each option. Assuming the cost sat-
isfies the uniform distribution, the utility function can
be expressed as:
U =
Z
max([C])
min([C])
xp(x)dx =
max([C]) + min([C])
2
(13)
where [C] is either [C
re
] or [C
by
] to calculate the utility
while x and p(x) are samples in the cost interval and
its probability. Finally, the option with a smaller U is
chosen as the navigation strategy.
5 SIMULATION EXPERIMENTS
We first conduct individual modules evaluation in
simulation, and then compare our method with the
state of the art before demonstrating a real robot ap-
plication.
5.1 Simulation Environment
We implement our method in two simulated envi-
ronments, a simple room and a large warehouse, as
shown in Fig. 4. The room environment is built on Py-
Bullet (Coumans and Bai, 2021) while the warehouse
is based on Gazebo (Koenig and Howard, 2004).
There is one MO in the room while multiple MOs are
randomly put in the blue regions in the warehouse to
simulate the variety of MO positions. A wheeled mo-
bile robot with an arm needs to complete navigation
tasks to reach the red goal. A LiDAR and a stereo
camera are used to localize the robot and detect MOs
respectively.
Figure 4: Simulation environments. Two environments are
used including a simple room and a complex warehouse.
The blue regions are possible places for the MOs and the
red region is the goal.
5.2 Implementation Details
We use ROS Noetic (Stanford Artificial Intelligence
Laboratory et al., 2018) with Movebase as the nav-
igation framework. The environment map (includ-
ing only static obstacles) is generated using GMap-
ping (Grisetti et al., 2007) and provided to the robot
as prior knowledge. We use A* (Hart et al., 1968)
as the global path planner and TEB (R
¨
osmann et al.,
2015) as the local path planner. The AMCL package
is employed to localize the robot from LiDAR data.
The robot detects MOs by Aruco Marker (Romero-
Ramirez et al., 2018) to reduce the classification un-
certainty.
All the experiments are implemented in Python
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
144

with PyTorch (Paszke et al., 2017). We use an Intel
i7-12700H CPU with 16G memory for the quantita-
tive results.
5.3 Bypass Time Regression Results
To demonstrate the improved bypass time prediction,
we compare the GLR regression model with the av-
erage speed method from (Zhang et al., 2023) and a
trapezoid method that considers acceleration and de-
celeration. We collect a dataset manually by con-
trolling the robot using a joystick and recording the
planned path and corresponding time, including 1500
trajectory segments as training and 600 as testing.
The average speed method calculates the speed in the
training dataset, then applies it in the test set. For the
GLR method, the model is fitted on the training set to
predict on the test set. We calculate the absolute error
between the predicted and actual navigation time. The
results in Fig. 5 show that the applied GLR method
outputs more accurate estimation with the lowest me-
dian absolute error (1.59s), compared to the average
speed (3.43s) and trapezoid methods (3.31s). Ad-
ditionally, the GLR method is more stable, with an
interquartile range (IQR) of 0.69s, versus 1.35s and
1.91s for the other methods. In the case study, we
found that the large error in the average speed method
arises from its neglect of acceleration and deceler-
ation during navigation. In contrast, the trapezoid
method accounts for the time spent in speed changes
and therefore yields smaller errors than the average
speed method. However, for paths with multiple an-
gle changes, the trapezoid method’s initial assump-
tion, allowing only a fixed number of accelerations
and decelerations, limits its adaptability. By compari-
son, our GLR method incorporates trajectory smooth-
ness, enabling it to capture the key factors influencing
navigation time and thus achieve the lowest prediction
error.
5.4 Action Uncertainty Module
Evaluation
To evaluate the effectiveness of modeling action un-
certainty, we compare the task completion time with
(w/) and without (w/o) the action uncertainty module
in two cases: one with easy MOs (90% loading SR)
and one with hard MOs (20% SR). We test the meth-
ods in three setups: ABC, AB, BC. ABC (resp. AB
and BC) indicates three MOs are in regions A, B and
C (resp. 2 at AB and BC) in Fig. 4.
The results in Fig. 6 show that with easy MOs
(SR=90%), the w/o method takes less time in plan-
ning and making decision as it removes the MO at B
Figure 5: Boxplot of the absolute error of prediction re-
sults for the three bypass time prediction methods. The box
represents the interquartile range (IQR), with the lower and
upper edges indicating the 25th (Q1) and 75th (Q3) per-
centiles, respectively. The notch and orange line in the box
marks the median value of the absolute error. Whiskers ex-
tend to the smallest and largest values within 1.5 times the
IQR from Q1 and Q3.
Figure 6: Task completion time comparison on methods
with/without considering action uncertainty in three envi-
ronments, ABC, AB, BC. The top figure shows the case
with easy MO (high SR) while the bottom one shows the
hard MO (low SR).
directly. Conversely, the method w/ has the robot by-
pass B first to check MOs in A or C. If A and C are
also blocked, the robot returns and removes the MO
in B, requiring more planning and navigation time.
When MOs are hard to manipulate (SR=20%), the
method w/ bypasses all MOs due to the high potential
cost of the removal action, leading to faster naviga-
tion compared to w/o method that repeatedly attempts
to remove MOs regardless of the cost. As for the sta-
bility, the w/ method demonstrates much lower IQR
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval
145

with 2.53s for easy MOs and 1.35s for hard MOs,
compared to the w/o method’s 6.16s and 34.14s, re-
spectively.
5.5 Ablation Study on Bias Between
Estimated SR and Real SR
To obtain the initial SR value, we conduct prior ex-
periments, as explained in Sec. 4.3. However, the es-
timated and actual SR may differ, especially when as-
suming all MOs share the same SR. Since SR relates
to the estimated removal cost and affects the naviga-
tion strategy, we analyze the impact of errors in esti-
mating the SR. The results on the cases with and with-
out estimation bias in environment ABC are shown
in Table 1. All the values of running time in the ta-
ble are the average of 5 trials. In the method with
action uncertainty (w/), an unbiased SR estimation
gives the best navigation strategy with minimal time.
Even with biased estimation, the method w/ still out-
performs the method w/o, proving the effectiveness of
the proposed action uncertainty module.
Table 1: Average running time of methods with unbi-
ased/biased estimation on SR. The cell marked bold means
better result.
Estimated SR Real SR w/o (s) w/ (s)
Unbiased
0.90 0.90 68.99±4.42 93.80±4.53
0.50 0.50 98.31±21.81 94.19±12.86
0.20 0.20 164.15±80.89 85.14±1.92
Overall 110.48 91.04
Biased
0.90
0.20 164.15±80.89 168.19±39.50
0.50 98.31±21.81 109.24±15.91
0.50
0.20 164.15±80.89 113.46±22.17
0.90 68.99±4.42 91.03±6.95
0.20
0.50 98.31±21.81 85.57±2.31
0.90 68.99±4.42 84.45±2.42
Overall 110.48 108.66
Table 2: Average running time of method with/without
blockage uncertainty in two environments.
Methods
Env w/o (s) w/ (s)
AB 67.04±2.54 77.77±2.63
ABE 141.02±16.81 90.08±2.25
Overall 104.03 83.92
5.6 Blockage Uncertainty Module
Evaluation
To compare the impact of introducing the blockage
uncertainty module, we design two environments AB
and ABE for evaluation (with obstacles at the corre-
sponding positions shown in Fig. 4). Environment AB
demonstrates the difference of navigation strategy due
to blockage uncertainty while ABE illustrates the ad-
vantage of the blockage uncertainty module when an
unexpected MO appears on the detour.
The evaluation results in Table 2 report the mean
runtime of 5 trials. In environment AB, without con-
sidering the blockage uncertainty (w/o), the robot
bypasses all the MOs. In contrast, the w/ method
chooses to remove the MO in region B considering
the potential blockage risk of the detour in narrow
passage. In AB where no surprising MO appears, the
bypass takes less time than the removal. However,
in ABE, where an unexpected MO blocks the detour,
the method w/o bypasses the MO in region B, and the
MO in E (failing to find a suitable stock region for re-
moving E), finally it returns to remove the MO at B,
taking much longer time than the method w/ that re-
moves B initially. From the overall performance, the
method w/ is more efficient comparing to the method
w/o.
5.7 Overall Comparison
We evaluate the overall performance in the two sim-
ulation environments (Fig. 4), with configurations of
ABC, AB, BC, ABE, ABD, BCE in the warehouse.
The starting points and goal points are randomly se-
lected to create different navigation tasks. Then, we
compare our method with some baseline methods,
priority bypass (R
¨
osmann et al., 2015; Hart et al.,
1968), priority removal, random choice method and
LaMB (Muguira-Iturralde et al., 2023).
The priority bypass methods including
TEB (R
¨
osmann et al., 2015) and A* (Hart et al.,
1968), bypass all the obstacles but fail if there is no
alternative way to the goal. The priority removal
method refers to a category of NAMO methods (Ellis
et al., 2022; Wang et al., 2020), which removes the
MOs that block the path without considering the
removal cost. The random choice method chooses
to remove or bypass with a probability (0.5 in our
experiments). The LaMB method (Muguira-Iturralde
et al., 2023) is one of the latest methods considering
the partial observation constraints in NAMO tasks
but limited to small scale environments.
We record the running time of each method. Tasks
are marked as failed if the goal is not reached within
300 seconds. Results are shown in Fig. 7. In the room
environment, the only path to the goal is blocked by a
MO. Therefore, the bypass method (A*) always fails.
The NAMOUnc and priority removal methods com-
plete the task more quickly, with the priority removal
method slightly faster (77.68s vs. 79.56s) since it
takes less time to plan bypass and make decision. In
the warehouse environment, the NAMOUnc and the
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
146

Table 3: Overall performance comparison in the real environment. The columns marked bold represent the best results.
Env TEB(R
¨
osmann et al., 2015)
Priority
Removal
Random
Choice
NAMOUnc
(Ours)
ABC 300.00±0.00 96.33±9.01 115.34±14.58 137.69±13.19
BC 46.66±4.56 94.78±5.08 72.73±19.94 50.41±2.62
AB 61.11±4.90 97.94±5.72 107.44±22.40 72.56±2.09
Overall 135.93 96.35 98.5 86.88
Figure 7: Running time in two simulation environments (around 70 trials for each environment), the room (left) and the
warehouse (right). The outliers (circle around 300 in the figures) represent the failure cases. The orange line in the box marks
the median value.
Figure 8: Real environment setup. The blue regions marked
as A, B, C are possible positions of MOs. The red arrow
with G is the goal.
TEB methods finish the task with comparable time
cost but NAMOUnc has no failures.
6 REAL EXPERIMENTS
6.1 Environment Description
To evaluate the performance of our method in real ap-
plications, we use a Jackal differential mobile plat-
form in a small warehouse-like environment. As
shown in Fig. 8, there are maximum 3 MOs and the
robot should navigate to a goal G. It is equipped with
a LiDAR and a RealSense camera to observe the envi-
ronment, an arm to lift MOs and the control software
described in Sec. 5.2.
6.2 Experiment Results
We randomly pick goal points to create different
NAMO tasks and record the running time with dif-
ferent MO setups, including environments ABC (all
paths to the goal are blocked), AB and BC (at least
one path to the goal is feasible). The quantitative re-
sults are shown in Table 3, where each cell indicates
the average running time and corresponding standard
deviation on 5 repeated trials. The priority bypass
method (TEB) fails in the ABC environment because
it finds no feasible path to the goal. Although the pro-
posed NAMOUnc method does not achieve the best
result in every individual environment, it attains the
best overall performance across the three setups in
terms of average running time. This shows that it
achieves a good trade-off between completeness and
efficiency in the search for a solution.
7 CONCLUSION AND FUTURE
WORK
We have presented a NAMO framework capable of
planning task and motion under four kinds of uncer-
tainties related to observation, action, model and ob-
servability. Our planner jointly optimizes success rate
and running time. Experimental results in both sim-
ulation and real environments demonstrate its ability
to balance these objectives, suggesting potential ex-
tensions to optimize additional objectives like energy
and safety.
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval
147

A relevant perspective is to overcome simplified
assumptions. For instance, observation noise may
not always follow a Gaussian distribution, and ac-
tion failures can stem from various factors, such as
mechanical constraints that can depend on the obsta-
cles and the environment. We believe that with more
data collection, a more accurate model can be devel-
oped, such as a planner based on large language mod-
els (Honerkamp et al., 2024), enabling the proposed
method to provide more robust and effective solutions
for NAMO tasks.
ACKNOWLEDGEMENTS
The publication of this research was supported by the
National Natural Science Foundation of China [Grant
42101445] and the Director Foundation of Guang-
dong Laboratory of Artificial Intelligence and Digital
Economy(SZ) [Grant 25420001 and 24420004].
REFERENCES
Coumans, E. and Bai, Y. (2016–2021). Pybullet, a python
module for physics simulation for games, robotics and
machine learning. http://pybullet.org.
Curtis, A., Matheos, G., Gothoskar, N., Mansinghka, V.,
Tenenbaum, J., Lozano-P
´
erez, T., and Kaelbling, L. P.
(2024). Partially observable task and motion planning
with uncertainty and risk awareness. arXiv preprint
arXiv:2403.10454.
Denoeux, T. (2019). Decision-making with belief functions:
A review. International Journal of Approximate Rea-
soning, 109:87–110.
Ellis, K., Zhang, H., Stoyanov, D., and Kanoulas, D.
(2022). Navigation among movable obstacles with
object localization using photorealistic simulation. In
2022 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS), pages 1711–1716.
IEEE.
Feng, D., Harakeh, A., Waslander, S. L., and Dietmayer,
K. (2021). A review and comparative study on proba-
bilistic object detection in autonomous driving. IEEE
Transactions on Intelligent Transportation Systems,
23(8):9961–9980.
Garrett, C. R., Paxton, C., Lozano-P
´
erez, T., Kaelbling,
L. P., and Fox, D. (2020). Online replanning in be-
lief space for partially observable task and motion
problems. In 2020 IEEE International Conference on
Robotics and Automation (ICRA), pages 5678–5684.
IEEE.
Grisetti, G., Stachniss, C., and Burgard, W. (2007).
Improved techniques for grid mapping with rao-
blackwellized particle filters. IEEE transactions on
Robotics, 23(1):34–46.
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-
mal basis for the heuristic determination of minimum
cost paths. IEEE transactions on Systems Science and
Cybernetics, 4(2):100–107.
Honerkamp, D., B
¨
uchner, M., Despinoy, F., Welschehold,
T., and Valada, A. (2024). Language-grounded dy-
namic scene graphs for interactive object search with
mobile manipulation. IEEE Robotics and Automation
Letters.
Kaelbling, L. P. and Lozano-P
´
erez, T. (2013). Integrated
task and motion planning in belief space. The Interna-
tional Journal of Robotics Research, 32(9-10):1194–
1227.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems.
Kim, B., Wang, Z., Kaelbling, L. P., and Lozano-P
´
erez, T.
(2019). Learning to guide task and motion planning
using score-space representation. The International
Journal of Robotics Research, 38(7):793–812.
Koenig, N. and Howard, A. (2004). Design and use
paradigms for gazebo, an open-source multi-robot
simulator. In 2004 IEEE/RSJ IROS, volume 3, pages
2149–2154. IEEE.
Li, C., Xia, F., Martin-Martin, R., and Savarese, S. (2020).
Hrl4in: Hierarchical reinforcement learning for inter-
active navigation with mobile manipulators. In Con-
ference on Robot Learning, pages 603–616. PMLR.
Maier, S. F. and Seligman, M. E. (1976). Learned helpless-
ness: theory and evidence. Journal of experimental
psychology: general, 105(1):3.
Muguira-Iturralde, J., Curtis, A., Du, Y., Kaelbling, L. P.,
and Lozano-P
´
erez, T. (2023). Visibility-aware navi-
gation among movable obstacles. In 2023 IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 10083–10089. IEEE.
Pan, T., Wells, A. M., Shome, R., and Kavraki, L. E. (2022).
Failure is an option: task and motion planning with
failing executions. In 2022 International Conference
on Robotics and Automation (ICRA), pages 1947–
1953. IEEE.
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E.,
DeVito, Z., Lin, Z., Desmaison, A., Antiga, L., and
Lerer, A. (2017). Automatic differentiation in pytorch.
Romero-Ramirez, F. J., Mu
˜
noz-Salinas, R., and Medina-
Carnicer, R. (2018). Speeded up detection of squared
fiducial markers. Image and vision Computing,
76:38–47.
R
¨
osmann, C., Hoffmann, F., and Bertram, T. (2015). Timed-
elastic-bands for time-optimal point-to-point nonlin-
ear model predictive control. In 2015 european con-
trol conference (ECC), pages 3352–3357. IEEE.
Safronov, E., Colledanchise, M., and Natale, L. (2020).
Task planning with belief behavior trees. In 2020
IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), pages 6870–6877. IEEE.
Silver, T., Chitnis, R., Tenenbaum, J., Kaelbling, L. P., and
Lozano-P
´
erez, T. (2021). Learning symbolic opera-
tors for task and motion planning. In 2021 IEEE/RSJ
International Conference on Intelligent Robots and
Systems (IROS), pages 3182–3189. IEEE.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
148

Stanford Artificial Intelligence Laboratory et al. (2018).
Robotic operating system.
Wang, M., Luo, R.,
¨
Onol, A.
¨
O., and Padir, T. (2020).
Affordance-based mobile robot navigation among
movable obstacles. In 2020 IEEE/RSJ International
Conference on Intelligent Robots and Systems (IROS),
pages 2734–2740. IEEE.
Williams, C. and Rasmussen, C. (1995). Gaussian pro-
cesses for regression. Advances in neural information
processing systems, 8.
Wu, H.-n., Levihn, M., and Stilman, M. (2010). Navigation
among movable obstacles in unknown environments.
In 2010 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems, pages 1433–1438. IEEE.
Xia, F., Li, C., Mart
´
ın-Mart
´
ın, R., Litany, O., Toshev, A.,
and Savarese, S. (2021). Relmogen: Integrating mo-
tion generation in reinforcement learning for mobile
manipulation. In 2021 IEEE International Conference
on Robotics and Automation (ICRA), pages 4583–
4590. IEEE.
Zhang, K., Lucet, E., dit Sandretto, J. A., and Filliat, D.
(2023). Navigation among movable obstacles using
machine learning based total time cost optimization.
In 2023 IEEE/RSJ International Conference on In-
telligent Robots and Systems (IROS), pages 11321–
11327. IEEE.
Zhang, K., Lucet, E., Sandretto, J. A. D., Kchir, S.,
and Filliat, D. (2022). Task and motion planning
methods: applications and limitations. In ICINCO
2022-19th International Conference on Informatics in
Control, Automation and Robotics, pages 476–483.
SCITEPRESS-Science and Technology Publications.
NAMOUnc: Navigation Among Movable Obstacles with Decision Making on Uncertainty Interval
149