Satellite Navigation Constellation Optimisation Problem Deﬁnition for

the Application of Genetic Algorithms

Paula Pi

neiro Ramos

1 a

, Sebastian Bernhardt

1 b

, Helena Stegherr

2 c

and J

org H

ahner

2 d

DLR Galileo Competence Center, Oberpfaffenhofen, Germany

Universit

at Augsburg, Augsburg, Germany

Keywords:

Constellation Optimisation, Evolutionary Algorithms, GNSS, LEO-PNT, Multi-Objective Optimisation,

Navigation, Problem Characterisation.

Abstract:

Global Navigation Satellite Systems (GNSS) are used on a daily basis, providing Positioning, Navigation and

Timing (PNT) services for various applications ranging from smartphones over the ﬁnancial sector up to areas

such as aviation and space. Classical GNSS constellations positioned in Medium Earth Orbit (MEO) often

experience reduced performance in areas of low visibility like forests and cities. To rectify this, augmentation

constellations are deployed, improving the provided positioning accuracy. Recent proposals for augmentation

systems have often been based in Low Earth Orbit (LEO), which, for global coverage, require a large number

of satellites and are complex to design due to dependencies, coverage requirements and the large search space.

This makes the constellation design problem well-suited for applying Genetic Algorithms (GA) to ﬁnd an

optimal solution. However, previous research has only addressed highly constrained versions of the problem.

This paper presents an approach for applying GAs to constellation designs with a large search space. In

particular, the focus is on the description of the multi-objective ﬁtness function and the simulation necessary

for its evaluation, options for the solution encoding, and a discussion of algorithmic features applicable in this

scenario.

1 INTRODUCTION

Satellites have come a long way since the launch of

the ﬁrst satellite, Sputnik, in 1957. In today’s world

satellites have become a backbone of modern civilisa-

tion and are used for military as well as civilian appli-

cations on a daily basis, spanning a wide range, e.g.

telecommunication, television, internet access, recon-

naissance, earth observation, deep space telescopes

and Position, Navigation and Timing (PNT).

The focus of this work are PNT constellations

and mostly augmentative constellations supporting

Global Navigation Satellite Systems (GNSS). Cur-

rently, there are four GNSS constellations: Global Po-

sitioning System (GPS - USA), Global’naya Navigat-

sionnaya Sputnikovaya Sistema (GLONASS - Rus-

sia), Baidou (China) and Galileo (Europa). These

systems are mostly positioned in Medium Earth Orbit

(MEO) at an altitude between 19000 km and 23000

https://orcid.org/0009-0003-4169-1805

https://orcid.org/0009-0002-7411-0870

https://orcid.org/0000-0001-7871-7309

https://orcid.org/0000-0003-0107-264X

km, the only exception to this being Baidou, as it in-

tegrates augmentation satellites in the system in addi-

tion to MEO at Low Earth Orbit (LEO), Geostation-

ary Earth Orbit (GEO) and Geo Synchronous Orbit

(GSO). These MEO constellations are stable in their

constellation design and improvements are more fo-

cused on the onboard technologies. However, in ad-

dition to these constellations there are augmentation

constellations which are more varying and adaptive

in their constellation design and therefore in constant

development. These constellations enhance GNSS

performance in speciﬁc regions, such as the Indian

system Navigation with Indian Constellation (NavIC)

and the Quasi Zenith Satellite System (QZSS) over

Japan. Besides these regional systems, there are also

plans for new global constellations in LEO, on gov-

ernmental side as well as from commercial compa-

nies. Constellations in LEO come with certain advan-

tages, for example satellites can use less expensive

components due to less radiation, the launch costs are

reduced due to the lower orbits (400-2000 km) and the

strength of the signal reaching Earth is a lot higher.

However, there are drawbacks as well, for global cov-

Ramos, P. P., Bernhardt, S., Stegherr, H. and Hähner, J.

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms.

DOI: 10.5220/0013782000003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 329-339

ISBN: 978-989-758-770-2; ISSN: 2184-2809

329

erage the number of satellites needs to be higher than

for traditional GNSS constellations, also the satellites

need to correct their orbits more often due to atmo-

spheric drag at lower altitudes, causing them to have

a shorter lifetime than their MEO counterparts. (Li

et al., 2023)

These augmentative constellations are much more

suited for optimisation than classic GNSS constel-

lations, as either a speciﬁc region has to be im-

proved with a speciﬁc number of satellites or, on a

global scale for LEO, the same performance has to

be achieved with a minimal number of satellites. The

optimisation of constellations is important for multi-

ple reasons, while the primary objective for the end

user of a constellation would be improved perfor-

mance, for the operator it would be the reduction of

costs. Besides performance and costs another topic

that has become more important recently is sustain-

ability, one natural point is that a reduced number of

rocket launches will reduce the impact on the envi-

ronment. Furthermore satellites contain rare materials

and the long term effects of the residual materials of

them burning up in the atmosphere is currently barely

researched so until a better solution is found to retire

satellites it should be a goal to minimise their number.

In the following sections, the necessary back-

ground is provided to enable the understanding

of constellation design and performance indicators.

Then, an in-depth analysis of the optimisation prob-

lem is conducted before showing necessary prepara-

tions for the application of a Genetic Algorithm (GA).

2 BACKGROUND

Before describing the considerations necessary for the

application of GAs, the requirements and constella-

tion types for the optimisation approach are explained

in detail.

2.1 Need for Augmentation

There are some parameters that can be considered for

the optimisation of a constellation, but for navigation

constellations, the ﬁrst parameter to look at is the Di-

lution of Precision (DOP) value of the constellation.

The quality of a positioning solution is in direct cor-

relation with the DOP value of the constellation, it ac-

counts for the user aspect with the receiver position,

as well as the system design based on the satellite ge-

ometry. DOP measures the combined impact of satel-

lite geometry on both 3D position and time accuracy,

while Position Dilution of Precision (PDOP) mea-

sures only the effect on 3D position accuracy. PDOP

is chosen because it isolates the spatial position qual-

ity, providing a clearer assessment of how satellite ge-

ometry affects positioning without mixing in timing

errors. The PDOP is based on the relationship be-

tween the locations of the satellites in Line of Sight

(LOS) to the receiver. Within these lines of sight, a

reversed squared pyramid can be built between four

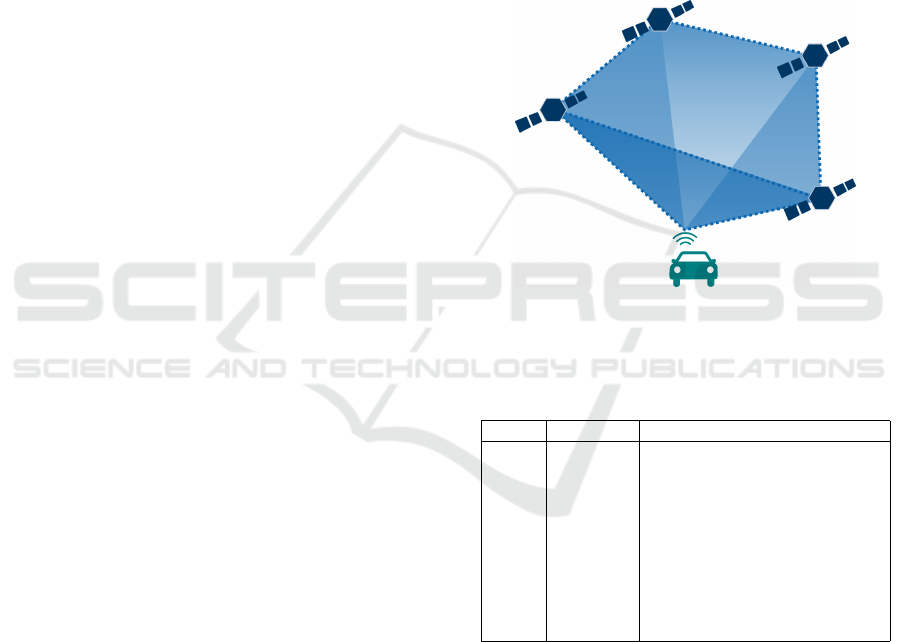
satellites and the receiver , this is shown in Figure 1.

Depending on the volume of the resulting pyramid,

the PDOP will change, a larger volume leading to a

smaller PDOP and thereby to a better positioning so-

lution. DOP values can be categorised depending on

their usability for positioning applications as shown

in Table 1.

Figure 1: Visualisation of geometry for the PDOP between

receiver and satellites.

Table 1: DOP ratings and classiﬁcation (Bernhardt et al.,

2024).

DOP Rating Classiﬁcation

<1 Ideal High conﬁdence for high preci-

sion

1-2 Excellent Appropriate for high precision

2-5 Good Minimum for accurate position-

ing

5-10 Moderate Minimum requirement for posi-

tioning

10-20 Fair Rough position estimation

>20 Poor Measurements should be dis-

carded

The global mean PDOP of Galileo is shown in

Figure 2. The data is analysed over one repeat orbit,

meaning that the ground tracks of the constellation

repeat themselves. For Galileo this happens every ten

days. This allows to make viable statements for the

behaviour of a constellation with a reduced data set.

The data in Figure 2 shows that the average PDOP

achieved by Galileo is around two, which is excellent

for positioning and, as most common receivers use

multi system GNSS, combining compatible systems

with each other, these values become even better.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

330

Figure 2: Visualisation of mean PDOP (values represented

by the colour bar) for Galileo. The stations were equally

distributed every 10° with a masking angle of 5°.

However, this only represents open ﬁeld conditions

with no constraints to visibility and a large part of

navigation in daily life happens in cities and, with

this, in urban canyons. In urban canyons, the masking

angles, depending on building height and positioning

of the user, can be much higher, reaching up to 90°

and by this greatly reducing the satellites in LOS (Xu

et al., 2020). Additionally, as MEO satellites appear

to move relatively slowly from an observer’s perspec-

tive on Earth, the conditions in a given location often

remain consistent over a long period. With the reduc-

tion of visible satellites this can increase the DOP by

a large factor (More et al., 2022) or even prevent po-

sitioning when the number of visible satellites falls

below four. The introduction of augmentation con-

stellations is meant to increase the number of visible

satellites. In the case of GEO satellites, these are in

a relatively ﬁxed position mostly at a very high angle

over the target region, while for LEO satellites, large

numbers combined with faster orbits lead to more fre-

quent changes in the geometry and a greater number

of visible satellites. Both approaches increase the per-

formance of GNSS in challenging environments.

Apart from the DOP, other optimisation objec-

tives that could be used for navigation constellations

or communication systems are, for example, visibil-

ity from a certain region for communication from a

ground station to a satellite, or the revisit time it takes

the satellite to come back to a certain location.

2.2 Constellation Types

Satellite constellation design is a complex problem,

as not only the individual orbits have to be chosen but

the different orbits have to be compatible as well. A

satellite’s orbit and its position on that orbit, is deﬁned

through the six Keplerian elements (cf. Figure 3):

semi-major axis, half of the major axis of the ellipse,

orbit eccentricity, indicating the deviation from a cir-

cular orbit, inclination of the orbit with respect to the

equatorial plane, longitude of ascending node, spec-

ifying where the orbit passes through the reference

plane, argument of periapsis, deﬁning the orientation

of the ellipse in the orbital plane and the true anomaly,

showing the current position of the satellite on the or-

bit.

Figure 3: Visualisation of Kepler Elements.

These elements offer an idealised representation

of the orbital plane of an object with respect to a refer-

ence plane and direction. Figure 3 describes an orbit

around an arbitrary body. Since the current satellite

constellations are focused on earth some further def-

initions can be made. The reference plane and direc-

tion are deﬁned as the equatorial plane and the vernal

equinox respectively. Additionally, for earth centred

orbits the terms apogee and perigee are used, as well

as Right Ascension of the Ascending Node (RAAN)

for the longitude of ascending node.

Since the description of a satellite orbit requires

all elements of each individual satellite to be deﬁned,

the number of variables quickly becomes impracti-

cal. To minimise the number of parameters required

to deﬁne a constellation, different design frameworks

have been developed to deﬁne relationships between

the satellites within a constellation. Some of the most

prominent constellation frameworks include Walker

(Delta/Star) constellations (Walker, 1970), Street-of-

Coverage (SOC) constellations (Beech and Dutruel-

Lecohier, 2013), and the newer Flower constella-

tions (Mortari et al., 2004).

J. G. Walker introduced two circular orbit constel-

lations in 1970, which set all orbital element apart

from the RAAN and true anomaly to the same value,

and have the orbital planes evenly distributed along

the equatorial line. The two constellation types dif-

fer in the plane distribution. The Walker Delta (cf.

Figure 4) has them distributed along the entire 360°,

while the Star pattern spreads them over 180°. In ad-

dition to the Keplerian elements of the ﬁrst satellite,

three constellation structure parameters are needed to

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms

331

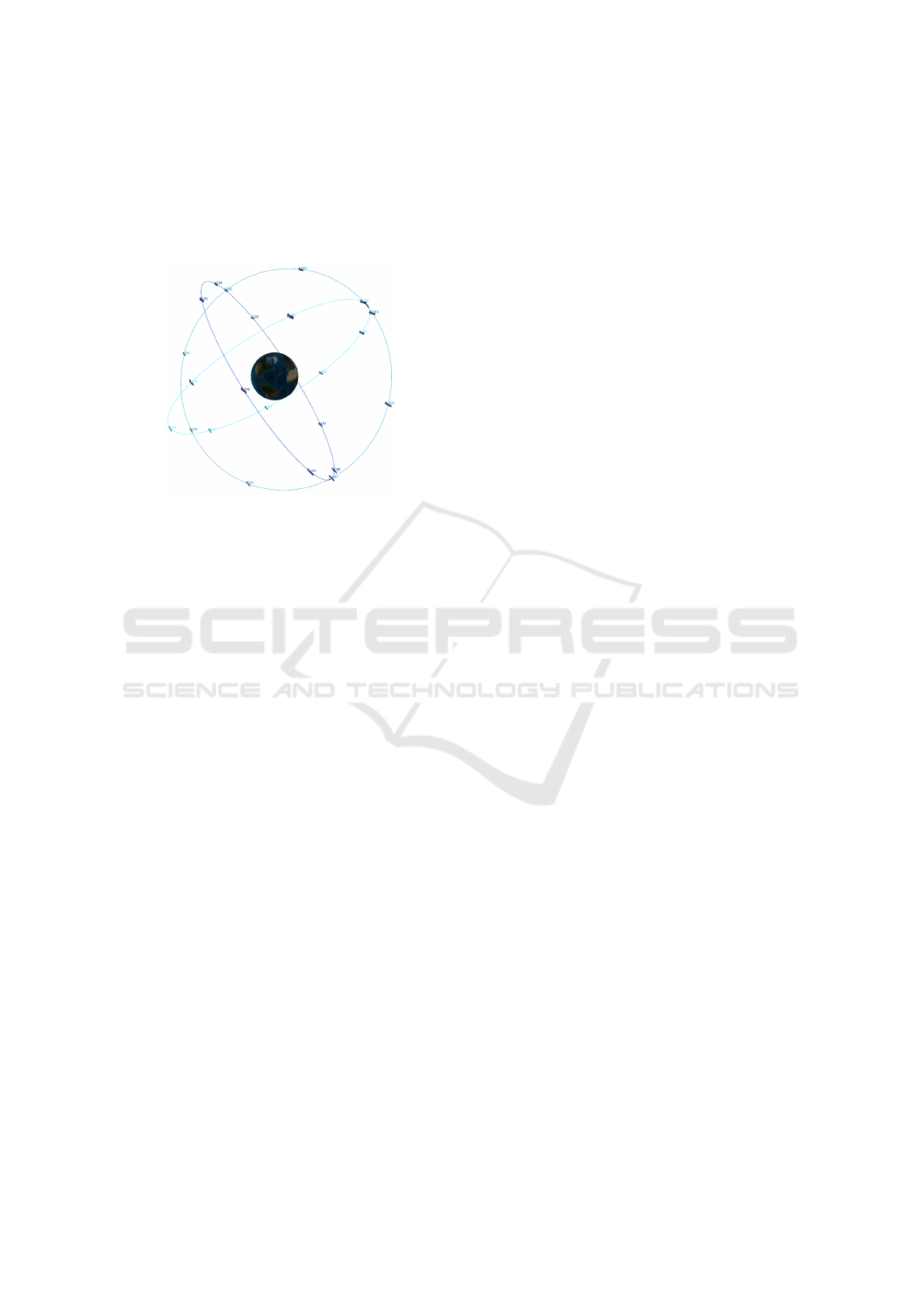
deﬁne a Walker constellation: the total number of

satellites, the number of orbital planes and the phase-

shift between adjacent planes. The Walker framework

can be used to describe most constellations, such as

for example the Galileo constellation (Delta) and the

telecommunication constellation Iridium (Star).

Figure 4: Visualisation of Walker Delta orbits at MEO in an

Earth Centered Inertial view.

Streets of Coverage constellations are one of the

few asymmetric constellations, distribution the orbits

heterogeneously along the equatorial line. Adjacent

orbits and satellites in the same orbit are synchronised

to offer swaths of coverage. The width of the swath,

also called ’street’ has to be set, along with the orbital

elements of the ﬁrst satellite. SOC constellations are

primarily used for communication.

The newer Flower constellations are designed to

have repeating ground tracks, meaning that after a

given time all satellites return to their initial posi-

tions. This property facilitates designing a constel-

lation for continuous coverage, since a complete con-

stellation analysis can be carried out in the time span

of one repetition (Nadoushan and Assadian, 2015).

To ensure repeating ground tracks, the framework sets

the orbital nodal period, the time needed for a satel-

lite to return to an orbital nodes, equal to the Green-

wich nodal period (24 hours). The Flower framework

creates very speciﬁc constellations and is therefore

mostly used for the derivation of more general rep-

resentations instead of directly in the design of a con-

stellation.

A derivation from the harmonic (symmetric) sub-

class of Flower constellation results in the Lattice

Flower frameworks, which seek to generalise mul-

tiple constellation types into one design framework.

The 2D Lattice theory combines Walker and Flower

constellations and requires the same parameters as the

Walker framework (Avenda

no et al., 2013). Having

set the initial values for the longitude of ascending

node and the mean anomaly, the positions of all satel-

lites are deﬁned by a two-dimensional system of equa-

tions. Expansion of the theory to higher dimensions

such as 3D and 4D is done to increase the degrees of

freedom of the design.

The 3D theory includes measures to counter the

effects of J

perturbations on the constellation orbits.

perturbation are the largest considered perturba-

tion effect caused by earths oblateness. These dis-

turbance in the gravity ﬁeld create forces, affecting

satellite orbits and distorting them over time, espe-

cially non-circular orbits. Instead of planning main-

tenance manoeuvres to upkeep the repeating ground

track, counter measures are included in the constella-

tion design. In the 3D representation, a term is added

for varying arguments of perigee, which accounts for

the rotation caused by J

perturbations (Davis et al.,

2013). The argument of perigee rotation changes the

relative position of the satellites in one orbital plane to

those in another, jeopardising coverage criteria. The

constellation can now be described using six integer

and six continuous parameters. The 4D Lattice frame-

work introduces an additional variation of the semi-

major axis of each orbit (Arnas et al., 2021). Usually,

varying satellite altitudes are introduced through dif-

ferent constellation layers, instead of different planes.

However, for some regional coverage scenarios, this

representation could be of use.

3 RELATED WORK

Due to the relevance of the ﬁeld, there have been

some past research efforts to develop an optimisation

method for satellite constellations (Choo et al., 2024).

Most literature focuses on the design of communica-

tion, navigation and earth observation constellations

with different types of coverage requirements: global,

regional or discontinuous regional coverage. Differ-

ent design approaches have been employed to iden-

tify optimal constellations, including simulation, ana-

lytical analysis and in recent years heuristic optimisa-

tion methods, such as GAs. Some of the objectives of

the optimisation are to minimise the number of satel-

lites as well as performance metrics such as the revisit

time and DOP values. In the following segment, lit-

erature designing navigation constellations based on

DOP values, as well and its limitations, will be re-

viewed. Some literature focuses on the minimisation

of the Geometric Dilution of Precision (GDOP), how-

ever for the reasons stated in Section 2.1 this paper

uses the PDOP.

Casanova (Casanova et al., 2014) attempts to re-

produce the Galileo constellation, using a basic GA,

a Particle Swarm Optimiser (PSO) and a coarse grid

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

332

enumeration and compares their results. While all

three algorithms produce promising results, they were

applied to a search space limited to eccentricity, incli-

nation, and argument of perigee alterations, and still

required a day and a half to reach convergence despite

the limitations.

Multi-objective constellation design is presented

in (Han et al., 2021) utilising a Multi-Objective Par-

ticle Swarm Optimiser (MOPSO) to minimise cost,

represented by the altitude, minimisation of the PDOP

and the maximisation of the number of visible satel-

lites. For the augmentative constellation, to be de-

signed, an altitude interval of 1000km is given and

only circular orbits are considered. The paper utilises

the 2D Lattice representation, ﬁxing the number of

satellites, as well as all orbital parameters except the

altitude and inclination. The MOPSO produces a con-

stellation with an improved homogeneous coverage,

but neglects the advantages a larger altitude range

and eccentric orbits have for global coverage (Ballard,

1980).

An example of a more complete optimisation is

presented in (Hitomi and Selva, 2018), which adds the

constellation size as a variable. Here, no constellation

framework is used, such that each satellite is placed

independently. But similarly to other publications, the

variable intervals are kept small with the semi-major

axis having a range of 600km and the satellite num-

ber being limited to twenty. Until now, no optimisa-

tion of the complete search space with large constel-

lations has been carried out, warranting further devel-

opments.

4 PROPOSED APPROACH

Having discussed basics and previous work in the

ﬁeld of constellation design, the following section

seeks to ﬁnd a suitable formulation for an optimiser

to solve the complete design problem.

4.1 Methodology Discussion

In (Casanova et al., 2014), single-objective optimisa-

tion is explored using the GDOP as the quality met-

ric, comparing a Simulated Annealing (SA) approach

with a classic GA. Here, the GA performs better in re-

gard to the given constellation design problem. Since

the design problem does not necessarily have a sin-

gle optimum (uni-modal), single-solution algorithms

such as SA relying on exploitation can get stuck in

local optima very easily. The exploration proper-

ties provided by population-based approaches, such

as GAs, help to avoid this issue, making population-

based algorithms the preferred methodologies for

high complexity problems, such as the one described

here. In most literature the design problem is run as

a single objective optimisation. While some papers

focus on the GDOP minimisation (Casanova et al.,

2014), in (Paek et al., 2019) a weighted sum of objec-

tives is used as the ﬁtness function, including constel-

lation cost and revisit time in addition to the GDOP.

Forming a weighted sum instead of using a multi-

objective algorithm simpliﬁes the program structure

and reduces computation time. However, due to a

signiﬁcant loss of solution quality the beneﬁts of the

simpler formulation are negated. So, while a single-

objective formulation can be used for an initial analy-

sis of the problem formulation and constellation rep-

resentation, an expansion to multiple objectives must

be incorporated at a later stage. The topology pre-

sented in (Choo et al., 2024) shows that in the con-

text of constellation design the focus lies on optimi-

sation algorithms such as PSO (Han et al., 2021)

and GAs (Whittecar and Ferringer, 2014), with arti-

cles such as (Casanova et al., 2014) and (Casanova

et al., 2012) comparing their performance. Gener-

ally, PSO shows higher ﬁtness results with faster con-

vergence, due to the deterministic nature of the up-

date mechanism compared to a generic GA (Casanova

et al., 2014). However, GAs are often preferred

for multi-objective optimisation, as extensive research

has gone into enabling simpliﬁed implementations

based on well-established base algorithms and pre-

deﬁned operators (Konak et al., 2006). Addition-

ally, there are enough well documented GA formu-

lations available, such as the Non-dominated Sorting

Genetic Algorithm 2 (NSGA-II) (Deb et al., 2002),

that allow an easy recreation of the base algorithms,

which can then be expanded and adapted for the spe-

ciﬁc use case. The wide variety of operators available

for GAs enables the improvement of the algorithm

to match, if not surpass the performance of multi-

objective PSO (Konak et al., 2006). Some potential

expansions of the algorithm include the introduction

of dynamic operator selection, and the reformulation

of the problem encoding into a variable-length chro-

mosome representation. This method is based on a

theory called building block hypothesis, which sug-

gests that constellations of different sizes will have

geometrical similarities like building blocks, mean-

ing constellations with similar orbital parameters will

also be similar in quality, even with different amounts

of satellites. The use of this representation allows

the inclusion of constellation size as a variable to

be optimised, avoiding the redundancies caused by

running separate optimisations for different constel-

lation sizes. (Hitomi and Selva, 2018) presents an ap-

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms

333

proach to using this method for constellation design,

introducing the necessary constellation representation

and operators to solve the problem. While the pa-

per demonstrates a signiﬁcant reduction of redundan-

cies when optimising for a given range of constella-

tion sizes, and therefore a reduced computational ef-

fort and increased convergence rate, the novelty of the

method introduces a few concerns. Neither the oper-

ators nor the representation presented in (Hitomi and

Selva, 2018) can be directly applied to the problem

formulation chosen for this setting, making the cre-

ation of new operators necessary. While the advan-

tages warrant further research into the use of variable-

length chromosomes, particularly for a broad constel-

lation size search space, it will not be a part of the

initial algorithm.

4.2 Constellation Representation

As discussed in Section 2.2, using an existing constel-

lation framework simpliﬁes optimisation immensely

due to the minimisation of the variables to be op-

timised. Ideally, the framework is formulated as

generic as possible to avoid exclusion of good per-

forming constellations. This is best done using the

Lattice Flower constellations, and since elliptical or-

bits should not be excluded, either the 3D or 4D for-

mulation has to be used. The 3D Lattice constellation

includes classical Walker, as well as elliptic Walker,

harmonic Flower and Draim constellations, only leav-

ing out non-symmetric constellations such as non-

harmonic Flower and SOC constellations. While 4D

provides the most generalised option, allowing differ-

ing semi-major axes, the complexity of the formula-

tion is not deemed worth it (Arnas et al., 2021). The

augmentation constellation to be designed is meant

as a single purpose constellation used for GNSS en-

hancement, and the variation of the semi-major axis

within a shell does not seem likely to provide higher

performance results for such a constellation, but in-

stead just an increase in launch cost and constellation

maintenance. A possible addition of further constel-

lation shells at different altitudes does not require a

4D representation. A representation including non-

symmetric constellations is presented in (Davis and

Mortari, 2012) but would need to undergo further re-

search to be used, therefore the non-symmetric con-

stellations have to be analysed separately. Since the

3D Lattice, while yielding good results (Xu et al.,

2022), is a new approach and requires more param-

eters, the 2D representation (Casanova et al., 2014;

Han et al., 2021) will be used initially to validate the

algorithm and ﬁtness function formulation. The later

expansion of the algorithm to incorporate additional

variables for the 3D lattice poses no issues, and the

constellation creation module simpliﬁes implement-

ing new constellation frameworks. An in-depth ex-

planation of the generation module is given in Sec-

tion 4.5. For the deﬁnition of a 2D Lattice Flower

constellation, three integer values and six continuous

orbital elements are needed. The integers to be de-

ﬁned are the number of satellites per plane, the num-

ber of planes and the phasing parameter. These vari-

ables introduce some dependencies that complicate

the inclusion into the optimiser loop. Firstly the satel-

lites have to be evenly distributed between planes, so

the total number of satellites has to be a multiple of

the number of planes. While using the number of

satellites per plane as a parameter instead of the to-

tal number of satellites does avoid this dependency,

new issues pertaining the parameter bounds are intro-

duced. Instead of introducing these dynamic bounds,

a correction function is used to round to the closest

integer that is a multiple of the number of planes. Ad-

ditionally the phasing parameter, describing the rela-

tive phasing between satellites on different planes, has

to be an integer smaller than the number of planes.

To ensure this, a second ﬁxing function introduced

in Section 4.3 is used. Since the Phasing parameter

inﬂuences the position of the satellites, it not only af-

fects coverage related metrics, such as the DOP and

number of visible satellites, but additionally has an

impact on the intra-constellation collision risk, deter-

mined by the distance between satellites. To minimise

the risk, (Liang et al., 2021) selects the phasing pa-

rameter to maximise the minimum distance between

satellites during the course of their simulations. Colli-

sions are unlikely to occur during the simulation peri-

ods, since they are mostly caused by small deviations

of the satellite positions over the long term operation

of a constellation. So, for the design of an operable

constellation, the collision risk should be taken into

account. This can be done by excluding the phas-

ing parameter from the optimisation and selecting it

as described in (Liang et al., 2021), or by including

the collision risk as an objective to be minimised. To

choose the adequate approach, the inﬂuence of the

phasing parameter on the remaining objectives needs

to be quantiﬁed, to see whether it is negligible or if

the phasing parameter needs to remain as an optimi-

sation variable. The necessary sensitivity study will

be carried out during later iterations of the approach

presented in this paper.

Excluding the phasing parameter from the opti-

misation would still leave the number of planes and

satellites as integer values. This introduces the ad-

ditional complexities of mixed integer programming.

To consider the desired data types of the different pa-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

334

rameters, they are written in, and read from an input

ﬁle. Since only continuous intervals are considered,

the values marked as integers are rounded after ap-

plication of the mutation operator. In addition to the

integer parameters, the six orbital elements of the ﬁrst

satellite have to be optimised. With these parame-

ters a single layer constellation can be created. How-

ever, multi-layer or multiple shell constellations can

be advantageous for a lot of applications, since having

satellites at different altitudes can combine the higher

signal strength of LEO satellites and greater coverage

of, for example, MEO constellations. Adding another

shell encompasses the full optimisation of an addi-

tional constellation, which can be done by extend-

ing the parameter list with further sets of constella-

tion parameters. This, however, means each shell is

part of the optimisation instead of allowing the num-

ber of layers to be an optimisation parameter itself.

The variable length chromosome representation can

be applied in this scenario. (Hitomi and Selva, 2018)

present an approach to optimising a constellation by

deﬁning each satellite individually. However, as dis-

cussed previously, an optimisation without the use of

a framework would cause enormous computational

costs as well as complications in the dynamic com-

patibility of the satellites, meaning this representation

cannot be seriously considered for the optimisation of

large constellations. Instead the satellite deﬁnitions

could be replaced by different constellations layers,

enabling the creation of multi-layer constellations.

4.3 Update Mechanism and

Termination

Choosing not to implement a variable-length chro-

mosome representation simpliﬁes the operator choice

considerably, as existing, well researched operators

can be used in the algorithm, and it is possible to

rely on a program structure that has been tested for its

quality and convergence. (Hitomi and Selva, 2018)

present two operators speciﬁcally designed to deal

with the chromosome length, which can be further

analysed when considering the expansion to multi-

layer constellation design. The implementation of the

NSGA-II includes selection, mutation and crossover

operators that are written to allow external alteration

of their hyperparameters. Tournament selection is

carried out to sample the parent individuals to be al-

tered. For this a batch of parents is sampled and the

one with the highest rank and lowest crowding dis-

tance is chosen to create offspring. The batch size

can be adapted to make the algorithm more or less

elitist, with the default being set to binary tourna-

ment selection. Two-point crossover is used unless

there are fewer than four parameters, in which case

NSGA-II falls back to one-point crossover. Since in-

equality constraints can be set between parameters, a

correction function is used in the case that a viola-

tion is caused due to crossover results. The correc-

tion function chooses a new parameter value from a

normal distribution centred at the violated boundary.

Mutation of the parameters is carried out based on

a truncated normal distribution with the mean set at

the parameter of the parent. Sampling from the trun-

cated distribution avoids having to rely on a correction

function to ﬁx parameters outside the allowed bounds.

The standard deviation can be adjusted to favour ex-

ploration or exploitation.

The main focus of (Hitomi and Selva, 2018) lies

on the variable-length chromosome representation,

but it additionally proposes a tool for Adaptive Oper-

ator Selection (AOS). The selection process consists

of a credit assignment and operator selection strategy,

meaning the performance of each operator is moni-

tored over a given amount of generations and given

a score. The operator performance is measured by

the quality of solutions produced, as well as the oper-

ator’s exploration ability, this is important to escape

local optima (Wei et al., 2023). Based on the as-

signed score the algorithm prioritises the use of high-

performance operators, while allowing some explo-

ration for possible improvement of lower scored oper-

ators (Fialho, 2010). Consistently adapting active op-

erators can lead to an improved convergence and qual-

ity of the optimisation. In recent years, approaches

to utilise reinforcement learning for the design of a

selection strategy have been proposed (Aydin et al.,

2023). The implementation of AOS requires further

investigation.

Due to the large variety of constellation applica-

tions, no universal number of generations can be set

for termination. A value for the number of genera-

tions can be determined on a case by case basis, based

on a target ﬁtness value and the given search space.

Adapting these hyperparameters to the problem, can

help avoid unnecessary computational effort, while

also allowing the discovery of above threshold solu-

tions. Computational cost can be further reduced by

not only terminating after a ﬁxed number of genera-

tions, but in addition tracking the improvement per-

centage between generations and setting a minimum

for it. When the improvement ends up at a plateau,

and sufﬁcient convergence is assumed the optimiser

can terminate without having reached the maximum

number of generations.

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms

335

4.4 Fitness Function

While the optimiser formulation presented in this pa-

per can be used for any type of constellation, the focus

lies on augmentative constellations for GNSS. There-

fore, the ﬁtness function formulation and evaluation

will be based on the corresponding requirements. As

introduced in Section 2.1, the PDOP is used as the

initial objective metric, with the number of satellites

as an additional objective. For the design of an aug-

mentation constellation, the constellation to be opti-

mised would be analysed as an overlay to an exist-

ing GNSS constellation. The PDOP is a value ob-

tained for deﬁned ground stations on Earth’s surface

and measured periodically over the simulation period.

Therefore, the ﬁtness function needs to be formulated

to combine the obtained values in a way, that allows

to optimise for the coverage and improvement goals

set. In (Casanova et al., 2014), the GDOP is mea-

sured on 30 000 globally distributed ground stations

over a sixty second propagation period. The ﬁtness

function is then chosen so that the maximal GDOP

found is minimised. Taking the example of Galileo

seen in Figure 2, the above-mentioned ﬁtness formu-

lation could lead to improvements in the lower per-

formance areas, such as the poles, but would only be

slightly better in other areas of interest. A more re-

liable formulation to ensure the wanted results would

be to choose the mean PDOP as the ﬁtness. This al-

lows to optimise for a global improvement by evenly

distributing the measurements, but also makes refor-

mulation for regional improvements very straightfor-

ward; the prioritisation could simply be represented

by the ground station distribution without needing ad-

ditional objectives for the same metric. Once the cho-

sen constellation is propagated, the PDOP is calcu-

lated by an analysis module (cf. Figure 5).

Satellite constellations, however, are analysed

based on more than one metric, so an expansion to

multiple objectives as in (Han et al., 2021) is reason-

able. Having decided against a weighted sum of ob-

jectives, a different ﬁtness function has to be formu-

lated for each objective. Some of the objectives that

will be considered after the initial testing of algorithm

and problem formulation include revisit time and cost

of the constellation. The minimisation of revisit time

and improved visibility from speciﬁc locations are vi-

tal factors for effective communication with ground

stations. Both can be calculated and analysed with

the propagated orbits of the constellation.

The calculation of the constellation cost is a more

complex problem, as numerous factors have to be

considered for a complete representation. The main

part of the cost is made up of the individual satellites,

which can be considered by minimising the number of

satellites. Additionally, LEO satellites tend to be less

expensive when compared to satellites for higher or-

bits, both due to the launch cost as well as the satellite

cost itself. Another expenditure that is highly depen-

dent on the optimisation parameters is the cost of the

launch, as it is affected by the speciﬁc orbits as well

as the number of planes and satellites. (Han et al.,

2021) seeks to minimise the orbit altitude to avoid the

cost of launching to higher orbits, but a more com-

plete representation is given in (Huang et al., 2021).

They include the effects of the orbital inclination with

respect to the latitude of the launch site, ﬁnding that

for high inclinations the advantages gained from the

Earth’s rotation are negated. This means a minimal

difference between orbital inclination and latitude of

launch site is preferred. The maintenance costs occur-

ring throughout the life time of the constellation can

be taken into account as well. These consist of cal-

culating the manoeuvres needed to counter the orbit

degradation caused by atmospheric drag and J

per-

turbations. (Han et al., 2021) proposes a formula for

the cost of altitude maintenance for LEO satellites,

since for lower orbits the drag effects have to be con-

sidered. A formulation for the J

effects is not given

since only circular constellations are considered in the

article and a standalone constellation is analysed for

which only the relative position of the satellites within

the constellation is relevant, as the J

effects are taken

as uniform over the whole constellation. However,

the algorithm presented in this paper, is meant to be

able to optimise non-circular orbits as well, making

the perturbations non-negligible. The use of the 3D

Lattice representation should allow for minimal main-

tenance cost, but its effectiveness and the long-term

propagation with respect to the main GNSS constella-

tions will have to be further analysed. While the cost

factors already require a trade-off, combining them

into a single ﬁtness function would avoid the com-

plexities of adding further objectives.

The complete formulation of the constellation de-

sign problem is made to allow exploration of aug-

mentation constellations outside of LEO constella-

tions. LEO augmentation constellations have recently

gained prominence due to their potential to improve

positioning accuracy, particularly in urban canyons.

Tall buildings and narrow streets in urban canyons of-

ten degrade signals, cause disruptions due to blockage

and attenuation, and obstruct satellite visibility (More

et al., 2022; Xu et al., 2020), causing positioning inac-

curacies and outages. However, due to the disadvan-

tages of LEO constellations detailed in Section 1 an

analysis of other augmentation constellations is also

deemed necessary.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

336

4.5 Implementation

The optimisation will be implemented inside the Sys-

tem and Service Volume Simulation Environment

(S²VSE) (Bernhardt et al., 2024) developed at the

Galileo Competence Center. S²VSE is a modular

and ﬂexible simulation and performance analysis tool,

it enables the reproduction, analysis and study of

current and future PNT systems and services. For

evaluations different parameter can be adjusted to

meet conditions like changes in constellation, impact

of new technologies or external factors like space

weather, overall this allows the assessment and pre-

diction of Key Performance Indicators (KPIs) like ac-

curacy, availability, continuity and integrity. S²VSE

is based on individual modules, which are mainly im-

plemented in Python and are connected via RCE (Re-

mote Component Environment).

The workﬂow, as depicted in Figure 5, starts with

the provision of a baseline constellation for the opti-

miser, which can either already be a multi-layer sys-

tem or a single layer constellation. Each layer of the

system is described in its own input ﬁle, based on the

characteristic of the layer like number of planes and

satellites per plane, these are then forwarded to the

constellation generator. This module will take the pa-

rameters from each ﬁle and sets up the complete con-

stellation for propagation. Currently, the propagation

is done via a third-party software the General Mis-

sion Analysis Tool (GMAT) provided by the National

Aeronautics and Space Administration (NASA). In

order to circumvent some constraints of the software

there are ongoing efforts to transition to an alterna-

tive solution that is being developed internally. The

duration of the propagation is dependent on the cre-

ated constellation and has to cover a complete repeat

orbit. After the propagation ﬁnishes, the data will be

parsed in a format to be compatible with the subse-

quent modules. At this point, visualisations can be

created, showing the resulting ground tracks or the

orbits. The next step is the calculation of the DOP

values. For this, in addition to the orbit data, the po-

sition of the receiver is necessary. The receiver can

be either a real location, an arbitrary number of re-

ceivers split over an area or a multitude of receivers

purposefully placed to create a certain scenario. Af-

ter the values have been calculated, the results can be

shown either as a plot of a region or as line charts for

each single receiver. The DOP values are also used

as input data for the optimiser to start the next itera-

tion of the loop with the goal to achieve an optimal

solution. Aside from the visualisation mentioned, the

data of each module can also be saved as a data ﬁle

and then used for additional analysis.

5 EXPERIMENT

5.1 Experimental Setup

The validation of the problem deﬁnition and workﬂow

set-up was carried out using the NSGA-II (Deb et al.,

2002) on a simple scenario. A Walker Delta constella-

tion is to be optimised for minimal PDOP achievable

with the minimum number of satellites.

Table 2: Constellation parameters. LB and UB describe the

upper and lower bounds, respectively.

Parameter LB UB

Number of Planes 4 20

Number of Satellites 32 400

Phasing Parameter 1 -

Semi-major axis 6771 km -

Argument of periapsis 0° -

Eccentricity 0 -

Inclination 45° 135°

Right Ascension 0° -

True Anomaly 0° -

All but three parameters were initially ﬁxed and

a limited search space was given for the parameters

to be optimised. The NSGA-II based optimiser was

set to have a population size of 30 constellations and

to terminate after 20 generations. To cover one re-

peat orbit, as explained in Section 2.1, the simulations

were set up to cover a time span of three days. Since

the time to repeat an orbit is dependent upon both alti-

tude and inclination, the maximum time interval was

selected to accommodate the chosen parameters. The

satellites were propagated with time steps of two min-

utes to reduce the time needed for simulations, while

still having multiple epochs during each overﬂight per

satellite. Even with reduced propagation time and the

coarse step size simulation time is around 30 min-

utes for each constellation. Relying on parallelisation

to run all constellations of a generation at the same

time it takes 30 minutes per generation and around 10

hours for one optimisation run, this will also change

depending on how many receiver are considered dur-

ing the PDOP analysis. For the initial scenario a sin-

gle station was simulated without any regard to Non-

Line of Sight (NLOS) situations, which will be cov-

ered in more detailed follow up scenarios. The ﬁt-

ness of a constellation is calculated by averaging the

PDOP values obtained at each time step and penal-

ising the constellations with discontinuous coverage.

The penalisation consists in setting the average PDOP

to 10000 and the number of satellites to the maximum

allowed, essentially disabling the constellation.

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms

337

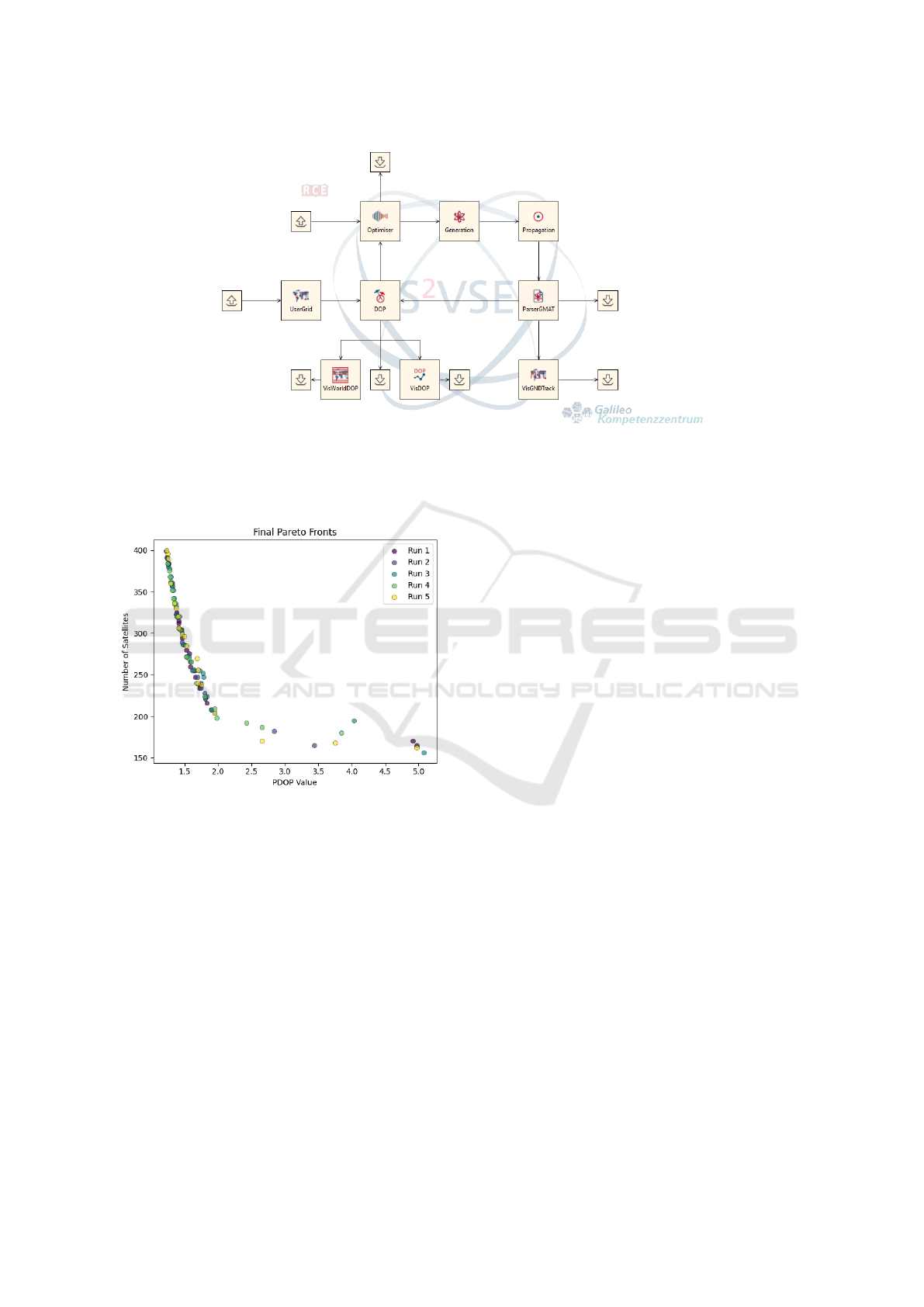
Figure 5: Workﬂow for the optimisation of constellations in regards to DOP values.

5.2 Simulation Results

Figure 6: Final Pareto front based on the results of ﬁve sim-

ulation workﬂows.

Figure 6 shows the Pareto fronts for the problem

described in Section 5.1, generated by running the

NSGA-II ﬁve times. The algorithm gives consistent

and plausible results, as visible in the front created

by the different runs and the fact that the PDOP fol-

lows the expected outcome for different numbers of

satellites. However, an ideal constellation can not be

chosen with the given set up, since more application

speciﬁc information has to be known to pick from the

front. This would include for example, more precise

data on constellation cost and budget, as well as the

required PDOP values.

6 DISCUSSION

The long simulation times, especially when consider-

ing global coverage and large receiver grids, required

constraints for initial testing, as shown in Section 5, to

provide justiﬁcation for more computationally expen-

sive optimisations. The provided results encourage

expanding the simulation scenarios to be able to cover

a broader range of use cases. This expansion should

also include a switch to a more general constellation

framework and the optimisation of more parameters

with larger intervals. Additionally, more objectives

should be introduced to consider more factors impact-

ing constellation design. Since more than three objec-

tives will be relevant, implementations of additional

GAs, such as NSGA-III and Strength Pareto Evolu-

tionary Algorithm II (SPEA-II) will be compared to

the current Algorithm. Due to the complexity of the

problem, the used algorithms need to be expanded to

improve the operators and their use. A static, gen-

eration dependent hyperparameter adjustment will be

used and later expanded to adaptive operator selec-

tion. As mentioned in Section 4.2, an implementation

of the 2D Lattice Flower representation and subse-

quently the 3D representation for perturbation con-

siderations will be used. However, the continuous

coefﬁcient representation (Davis and Mortari, 2012)

should also be considered, as it includes non-uniform

representations, in addition to the uniform constella-

tions included in the 3D Lattice representation. For

the optimisation of multi-layer constellations the vari-

able length chromosome representation will be inves-

tigated. This paper shows that the utilisation of GAs

could give insights into future possibilities in the ﬁeld

of augmentative PNT constellations and aid the com-

plex constellation design process.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

338

ACKNOWLEDGEMENTS

This work was partially funded by the Deutsche

Forschungsgemeinschaft DFG (HA 5480/10-1).

REFERENCES

Arnas, D., Casanova, D., and Tresaco, E. (2021). 4d lattice

ﬂower constellations. Advances in Space Research,

67:3683–3695.

Avenda

no, M., Davis, J., and Mortari, D. (2013). The 2-

D lattice theory of Flower Constellations. Celestial

Mechanics and Dynamical Astronomy, 116:325–337.

Aydin, M. E., Durgut, R., and Rakib, A. (2023). Adaptive

operator selection utilising generalised experience.

Ballard, A. H. (1980). Rosette constellations of earth satel-

lites. IEEE Transactions on Aerospace and Electronic

Systems.

Beech, T. and Dutruel-Lecohier, G. (2013). A study of three

satellite constellation design algorithms.

Bernhardt, S., Eiselbrecher, F., and Schmidt, A. (2024).

System and service volume simulation environment

s²vse. In Proceedings of the 37th International Tech-

nical Meeting of the Satellite Division of The Institute

of Navigation (ION GNSS+ 2024), pages 855–866.

Casanova, D., Avendano, M., and Mortari, D. (2012). Op-

timizing Flower Constellations for Global Coverage.

In AIAA/AAS Astrodynamics Specialist Conference

2012.

Casanova, D., Avenda

no, M., and Mortari, D. (2014). Seek-

ing GDOP-optimal Flower Constellations for global

coverage problems through evolutionary algorithms.

Aerospace Science and Technology, 39:331–337.

Choo, N., Ahner, D., and Little, B. (2024). A Survey of Or-

bit Design and Selection Methodologies. The Journal

of the Astronautical Sciences, 71.

Davis, J., Avenda

no, M., and Mortari, D. (2013). The 3-

D lattice theory of Flower Constellations. Celestial

Mechanics and Dynamical Astronomy, 116:339–356.

Davis, J. and Mortari, D. (2012). Reducing walker, ﬂower,

and streets-of-coverage constellations to a single con-

stellation design framework. Advances in the Astro-

nautical Sciences, 143:697–712.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

NSGA-II. IEEE Transactions on Evolutionary Com-

putation, 6(2):182–197.

Fialho, A. (2010). Adaptive Operator Selection for Opti-

mization. PhD thesis, Universite Paris-Sud.

Han, Y., Wang, L., Fu, W., Zhou, H., Li, T., Xu, B., and

Chen, R. (2021). Leo navigation augmentation con-

stellation design with the multi-objective optimiza-

tion approaches. Chinese Journal of Aeronautics,

34(4):265–278.

Hitomi, N. and Selva, D. (2018). Constellation optimization

using an evolutionary algorithm with a variable-length

chromosome representation. In 2018 IEEE Aerospace

Conference, pages 1–12.

Huang, S., Colombo, C., and Bernelli-Zazzera, F. (2021).

Multi-criteria design of continuous global coverage

walker and street-of-coverage constellations through

property assessment. Acta Astronautica, 188:151–

170.

Konak, A., Coit, D., and Smith, A. (2006). Multi-objective

optimization using genetic algorithms: A tutorial. Re-

liability Engineering & System Safety, 91:992–1007.

Li, X., Jiang, K., and Li, P. (2023). Analysis of naviga-

tion augmentation performance based on leo satellite

communication constellation. In China Satellite Nav-

igation Conference (CSNC 2024) Proceedings.

Liang, J., Chaudhry, A. U., and Yanikomeroglu, H.

(2021). Phasing parameter analysis for satellite col-

lision avoidance in starlink and kuiper constellations.

In 5G World Forum Workshop on Satellite and Non-

Terrestrial Networks.

More, H., Cianca, E., and Sanctis, M. D. (2022). Position-

ing performance of leo mega constellations in deep ur-

ban canyon environments. In 25th International Sym-

posium on Wireless Personal Multimedia Communi-

cations (WPMC).

Mortari, D., Wilkins, M., and Bruccoleri, C. (2004). The

ﬂower constellations. The Journal of the Astronautical

Sciences, 52.

Nadoushan, M. J. and Assadian, N. (2015). Repeat ground

track orbit design with desired revisit time and optimal

tilt. Aerospace Science and Technology, 40:200–208.

Paek, S. W., Kim, S., and de Weck, O. (2019). Opti-

mization of reconﬁgurable satellite constellations us-

ing simulated annealing and genetic algorithm. Sen-

sors, 19(4):765.

Walker, J. G. (1970). Circular Orbit Patterns Providing

Continuous Whole Earth Coverage. Technical report,

Royal Aircraft Establishment Farnborough.

Wei, W., Xuan, M., Li, L., Lin, Q., Ming, Z., and Coello

Coello, C. A. (2023). Multiobjective optimization al-

gorithm with dynamic operator selection for feature

selection in high-dimensional classiﬁcation. Applied

Soft Computing, 143:110360.

Whittecar, W. and Ferringer, M. (2014). Global Coverage

Constellation Design Exploration Using Evolutionary

Algorithms. In AIAA/AAS Astrodynamics Specialist

Conference 2014.

Xu, H., Hsu, L., Lu, D., and Cai, B. (2020). Sky visibil-

ity estimation based on gnss satellite visibility: an ap-

proach of gnss-based context awareness. GPS Solu-

tions, 24.

Xu, X., Ju, Z., and Luo, J. (2022). Design of constellations

for gnss reﬂectometry mission using the multiobjec-

tive evolutionary algorithms. IEEE Transactions on

Geoscience and Remote Sensing, 60.

Satellite Navigation Constellation Optimisation Problem Deﬁnition for the Application of Genetic Algorithms

339