Design Space Exploration and Performance Evaluation of a

Multi-Chamber, Multi-Curvature Soft Actuator for

Robotic Applications

Ansari Usama and Asokan Thondiyath

Department of Engineering Design, Indian Institute of Technology Madras, Chennai, 600 036, India

Keywords: Soft Actuator, Robotic Gripping, Parameter Identification, FEM.

Abstract: Soft actuators are finding wide applications in robotics due to the compliance they offer in handling delicate

objects. The design of soft actuators is challenging due to the fragile nature of the materials used and the

difficulty of fabricating them. Also, soft actuators must be designed to achieve the desired bending

performance that suits the application. This paper presents the design and analysis of a multi-chamber, multi-

curvature soft actuator for robotic gripping applications. This design combines two different configurations

to get the desired bending curvature of the actuator. Modeling of the actuator and analysis of the effect of

various design parameters on the bending angle and the tip force are presented. Prototype fabrication and

experimental results are also presented. The results confirm that it is possible to custom-design soft actuators

to meet specific performance requirements through design synthesis.

1 INTRODUCTION

Soft robots offer inherent compliance by using soft

materials and novel structures to adapt to the

surrounding environment, improving flexibility and

adaptability. They take inspiration from nature, such

as the octopus, starfish, and jellyfish. Soft robots aim

to provide safe and compliant interaction with

humans (Wu et al., 2019; Rogóż et al., 2016). Unlike

traditional robots made from rigid links, joints, or

inflexible components, soft robots are built using

flexible and stretchable materials such as silicone

rubbers, elastomers, and soft polymers, enabling them

to achieve nearly infinite degrees of freedom,

conform to various shapes and sizes, and manipulate

fragile or irregular objects (Navas et al., 2021).

Traditional robotic grippers, made from hard

materials like metal or plastic, are well suited for

high-precision, repetitive tasks in structured

environments due to their fast response, stability, and

higher payload capacity. However, their limitations

become evident in unstructured environments or tasks

requiring delicate handling, such as grasping soft,

fragile, or irregularly shaped objects (Zhang et al.,

2019; Zhang et al., 2017). In contrast, soft grippers

excel by utilizing compliant materials and bio-

inspired designs to offer safer, more adaptable

grasping solutions (Zaidi et al., 2021). The

performance of soft grippers depends strongly on the

design and bending behavior of soft actuators, which

is the focus of this paper.

Various actuation methods for soft robots have

been explored, including electroactive polymers,

cable-driven systems, shape memory alloys, material

jamming, magnetic actuation, and fluidics

(pneumatic and hydraulic) (Su et al., 2022). Among

these, pneumatic actuation is most widely adopted

due to its simplicity, low cost, light weight, high force

output, and ease of fabrication (Gariya et al., 2023).

The typical structure of a soft pneumatic actuator

(SPA) consists of an extensible top layer with

embedded air chambers and an inextensible bottom

layer. When pressurized, the chambers expand and

push against each other, causing the actuator to bend

toward the inextensible side. To guide this

deformation in a desired direction, the actuator is

designed with differing material thicknesses between

the chamber top wall and the inextensible bottom

layer (Polygerinos et al., 2015).

SPAs can be either single-chamber or multi-

chamber. Single-chamber actuators are easy to design

and fabricate but tend to show significant radial

expansion or ballooning effects under pressure,

reducing precise control and efficiency (Gariya et al.,

116

Usama, A. and Thondiyath, A.

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications.

DOI: 10.5220/0013777000003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 116-127

ISBN: 978-989-758-770-2; ISSN: 2184-2809

2023; Ariyano et al., 2019). Fiber reinforcement was

introduced to overcome ballooning and enable

directional bending by constraining deformation

(Soft Robotics Toolkit, n.d.; Hu et al., 2018). Multi-

chamber designs were introduced to overcome the

difficulties with single-chamber actuators. A multi-

cavity soft pneumatic actuator was developed in (Lei

et al., 2022), and a theoretical model linking input

pressure to bending deformation was proposed.

Although the actuator demonstrated good flexibility,

it was limited to a fixed single-curvature

configuration. A structurally optimized multi-

chamber soft actuator was proposed in (Hu et al.,

2018), but it produces single-curvature bending.

There were multiple approaches in the design of

multi-chamber actuators through segmented control

(Yang et al., 2020), multi-composite structures

(Huang et al., 2021), and slow and fast pneumatic

networks (sPN/fPN) (Mosadegh et al., 2014). These

works demonstrate continued progress in improving

actuation performance and structural optimization,

yet most remain limited to single-curvature, single-

configuration outputs. Such actuators are unsuitable

for many robotic grasping applications because they

struggle to conform to irregular shapes or delicate

objects, point contact at the actuator tip, have limited

surface conformability, and the contact force

generated is less uniform (Tang et al., 2022). (Song et

al. 2021) achieved multi-curvature deformation by

dividing the multi-chamber actuator into several

chamber groups and actuating those selectively using

independent pressure channels. This enabled

programmable deformation patterns and improved

dexterity but required complex multi-channel

pneumatic control, increasing system-level

complexity.

Building on our earlier work (Ansari et al., 2025),

this paper proposes a multi-chamber, multi-curvature

bending profile soft actuator using a multi-curvature

design and a single pneumatic channel. The actuator

also integrates an adhesion mechanism to improve

further grasping stability and adaptability.

Performance metrics, including taper optimization,

contact uniformity, and object compatibility, are

evaluated through numerical simulations and

parametric studies, demonstrating advantages of this

approach over conventional single curvature designs.

The remainder of the paper is organised as

follows: Section 2 provides Methodology, Section 3

explains Parametric Study, Section 4 provides Bio-

mimicry in Soft Actuator Design with Suckers,

Section 5 provides Simulation Studies, Section 6

includes Prototyping and Testing, Section 7 Actuator

Testing for Grasping, and Section 8 provides

Conclusion and future work, followed by References.

2 METHODOLOGY

The design of the soft actuator is achieved by

combining design configurations of air chambers, as

shown in Figure 1. The series arrangement of

Configuration B–C–A is inspired by the work of

(Ansari et al. 2025), while Configurations A and B

are based on (Mosadegh et al. 2014), and

Configuration C draws inspiration from (Yang et al.

2020).

Figure 1: Sectional view of SPA for Configuration B, C, A.

Referring to Figure 1, Configuration A has no gap

between chambers, which leads to high stiffness and

limited bending. Configuration B has gaps present but

chambers are attached to the bottom plate, which

slows bending. In contrast, in Configuration C, the

chambers are detached from the bottom plate, leading

to fast, less restricted bending.

Therefore, the proposed design combines

Configurations B and C, with seven chambers for

Configuration B and five for Configuration C, as

shown in Figure 2. Figure 3 shows the cross-sectional

view of the actuator. Parameter identification and

performance analysis were done to identify the best

design parameters for the proposed design

configuration.

This process was done in two steps: first,

optimizing the taper angle by inclining the four lateral

faces of the rectangular cross-section inward, inspired

by tapering seen in octopus arms and elephant trunks,

which improves bending (Calisti et al. 2011), and

second, performing a parametric analysis of

geometric dimensions such as chamber gap, wall

thickness, and other structural parameters.

2.1 Design Variants for Taper

Optimization

A systematic design study was performed to identify

the best taper angle for the multi-chamber, multi-

curvature soft actuator. Several design variants were

defined by varying the inclination of the lateral faces

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

117

of the rectangular cross-section of the actuator

tapering on actuator performance, inspired by octopus

arms and elephant trunks. Figures 4(a) and (b) show

the taper angle variations proposed in this study.

Table 1 summarizes the different design variants,

their descriptions, and the sets considered to support

the selection of the optimal design variant for further

parametric analysis.

Figure 2(A): Sectional View with Configuration B & C.

Figure 2(B): CAD Model of SPA with Configuration B&C.

Figure 3: Sectional view of SPA at Section X-X.

Figure 4: (A) Taper Angle Variation for SPA (Top View).

Figure 4: (B) Taper Angle Variation for SPA (Front View).

2.1.1 Design Variant Simulation Study and

Ranking Methodology

A systematic simulation study was carried out to

evaluate the bending performance. Each design

variant was modelled with specific combinations of

taper angle. 64 variants were analyzed and labelled as

different “sets” (for example, Set B, Set C, Set D),

where each set denotes a taper condition for each

actuator variant, a finite element simulation was

conducted in Abaqus/CAE to evaluate the bending

deformation under applied internal pressure, where

the actuator was modelled using a hyperelastic

material model (Yeoh model) to capture its nonlinear

elastic behaviour, and the analysis was performed

using a nonlinear static step. Boundary conditions

were applied by fixing the base of the actuator, while

pressure loading was applied uniformly to the inner

chamber surfaces. Further details on the geometry,

meshing, material properties, and loading are

provided in Section 5.

The key parameters recorded along the effective

gripping length (from 40 mm to 100 mm) were:

• Bending angle (θ): the angular change between

the base and tip,

• Slope of the actuator (s): the average angular

gradient along the curved body,

• Tip deflection (d): the vertical displacement of

the actuator tip from its original position, as

shown in Figure 5.

Figure 5: Illustration of actuator deformation parameters.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

118

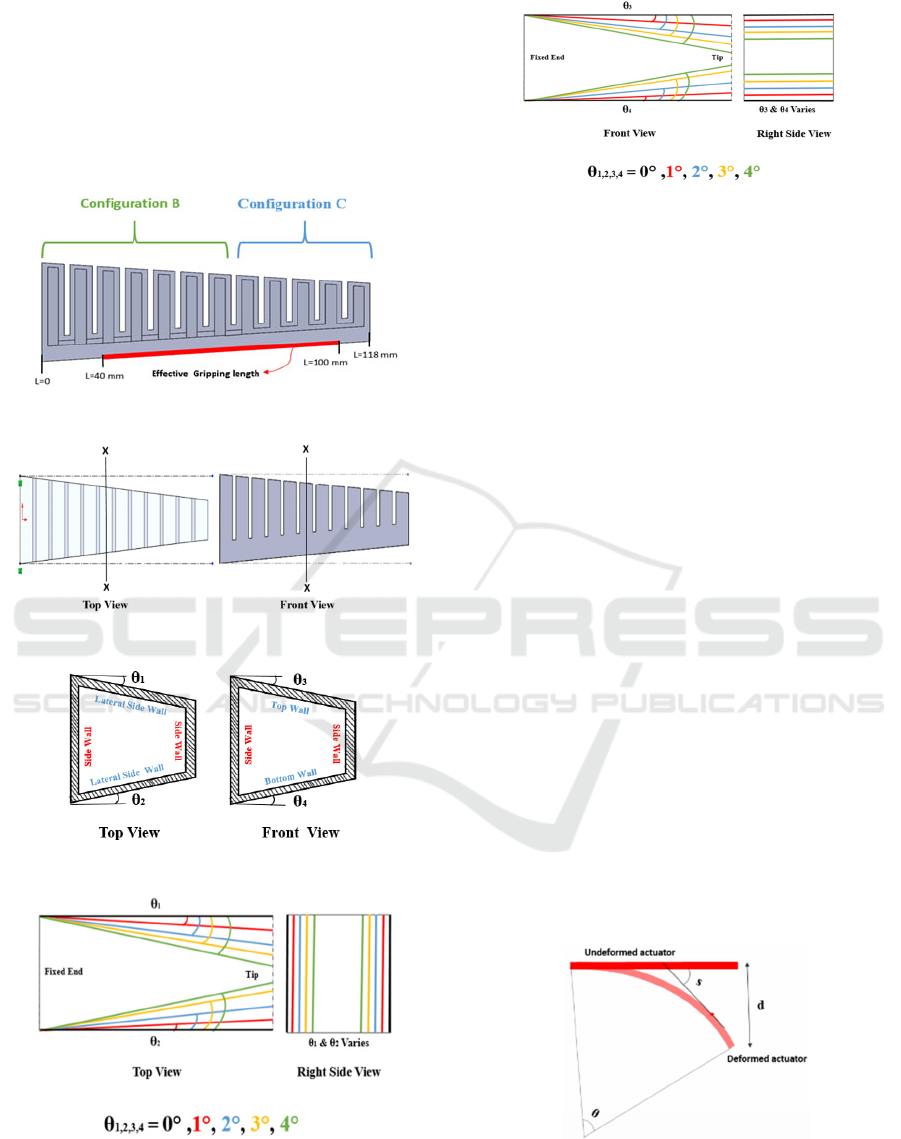
Table 1: Design variants considered for taper angle optimization in multi-chamber soft actuator.

Design

Varian

Description Set (At Section X-X)

1 All four faces varied from 1°– 4° taper, forming

sets A – D based on different taper assignments. 4

combinations formed. (1 variation per set).

2 One face fixed at 0°, other three faces varied from

1°–4° taper, forming sets A–D. 16 combinations

formed (4 sets × 4 taper variations in each set).

3 Two faces fixed at 0°, other two faces varied from

1°–4° taper, forming sets A–F. 24 combinations

formed (6 sets × 4 taper variations in each set).

4 Three faces fixed at 0°, one face varied from 1°–4°

taper, forming sets A–D. 16 combinations formed

(4 sets × 4 taper variations in each set).

5 All four faces tapered differently, with angles of 1°,

2°, 3°, and 4° assigned in permutations to form sets

A–D. 16 combinations formed (4 sets × 4

permutations).

V denotes a face with taper angle varied from 1° to 4°

in the stud

0 denotes a face with zero angle.

A multi-criteria ranking metric was developed to

objectively compare the variants, based on two

criteria: average performance and uniformity of

bending.

The scoring was calculated as follows:

Final Score = 0.5×Average Weighted Score +

0.5× (1−Average Normalized Variance) where, the

weighted score combines normalized values of

bending angle (0.4 weight), slope (0.3 weight), and

deflection (0.3 weight), this weight is assigned based

on the relative importance in grasping tasks.

Weighted Score=0.4× (Normalized Bending)

+0.3× (Normalized Slope) + 0.3×

(Normalized Deflection)

The normalization for bending, slope, and deflection

metrics was computed using min-max normalization,

i.e.

Normalized Value

 























where the min and max were computed across all

configurations over the effective gripping range (40

mm to 100 mm).

The Average Weighted Score is computed by

averaging the weighted scores across the seven

evaluation points in the gripping zone. The Average

Normalized Variance quantifies how consistently the

actuator performs along its length, by calculating the

variance of slope values normalized over the same

evaluation region.

Based on the final scores as in Table 2, Variant

4D with a 4° taper had the highest rank. However, its

asymmetric left-sided taper produced a diagonal or

inclined bending profile that was less suitable for

gripping. Therefore, Variant 3C with a 2° taper was

chosen, as both the side faces are tapered equally for

further experimental validation. This variant showed

a high bending angle, consistent slope distribution,

and a balanced deflection profile, making it better

suited for soft gripping applications where

predictable, symmetric bending is critical.

2.1.2 Taper Angle for Selected Design

Variants (3C2)

In this study, the actuator cross-section was

rectangular, and the tapering of the side faces was

varied to evaluate its effect on bending performance

Variants were categorized based on how many faces

were tapered and at what angle.

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

119

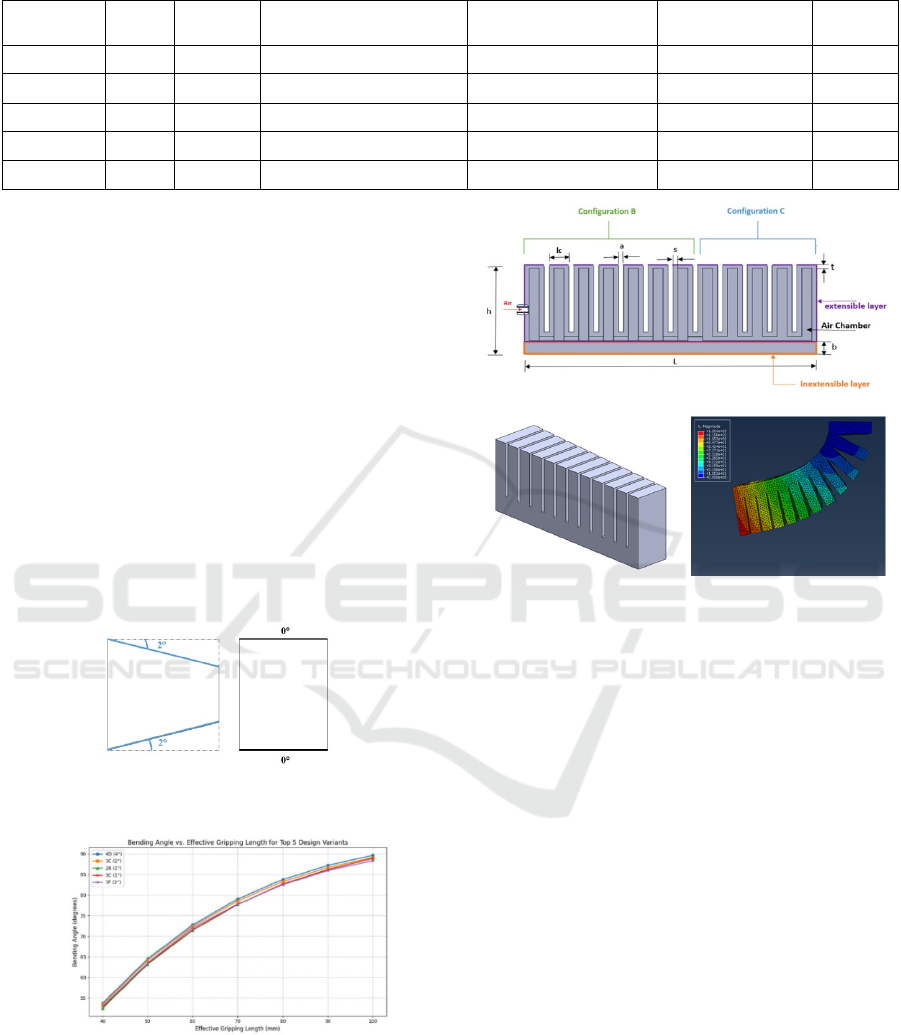
Table 2: Top 5 Ranked Design Variants Based on Weighted Performance Score and Normalized Slope Variance.

Design

Varian

Tape

Angle

Avg Weighte

Score

Avg Normalize

Slope Variance

Final Score Ran

4 D 4° 0.648 0.269 0.6729 1

3 C 2° 0.637 0.264 0.6667 2

2 B 1° 0.632 0.266 0.6626 3

3 C 1° 0.632 0.266 0.6626 3

3 F 2° 0.624 0.275 0.6543 5

• Design Variant 3: Two faces were fixed at 0°

(no taper), while the other two were tapered

at equal angles ranging from 1° to 4°.

• Set C of Variant 3 (3C): Corresponds to a

specific face arrangement where the top and

bottom faces are fixed at 0°, and the left and

right faces are tapered.

• 3C2: In this configuration, the left and right

faces were tapered inward at 2°, while the top

and bottom faces remained at 0.

• This design variant helps bending of actuator

inwards, as the tapered sides make it easier

for the walls to bend in that direction.

• Figure 6 illustrates the rectangular cross-

section from right-side and top views,

indicating the fixed and tapered faces (θ₁ = 0°,

θ₂ = 0°, θ₃ = 2°, θ₄ = 2°).

Top View Front View

Figure 6: Sectional Diagram for Design Variant 3C2.

Figure 7: Bending Behaviour for top design variant.

The selected Design variant 3C2 sectional view,

CAD model and simulation is shown in Figure 8

(a)

(b) (c)

Figure 8: (a) Actuator Sectional View and (b) CAD Model

for 3C-2 degree (c) Simulation.

3 PARAMETRIC STUDY (3C2)

A parametric study systematically investigates how

changing individual geometric parameters affects the

actuator’s bending behaviour and overall

performance.

The objectives of the study are:

1. Understand the Sensitivity: Know which

parameters significantly influence the

performance (e.g., bending angle, force, and

displacement).

2. Optimize the Design: Identify the best

parameters for desired performance (e.g.,

maximum bending angle).

3. Improve Efficiency: Reduce material cost,

air consumption, and increase reliability.

4. Design Guidelines: Propose guidelines for

future designs or prototypes.

To assess performance changes, two metrics were

used: Sensitivity (°/kPa), which measures how much

the bending angle changes per unit pressure (higher

values mean faster bending but harder control), and

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

120

R², which measures how well pressure predicts

bending (values near 1 mean more consistent and

reliable control)

The parameters examined include: chamber gap,

sidewall thickness, gap shape, actuator width, top

wall thickness, and bottom wall thickness. The results

and analysis for each parameter are presented in the

following subsections.

1. Chamber Gap

The chamber gap, i.e, spacing between adjacent

chambers, affects bending angle, sensitivity, and

control predictability. FEA results for 1 mm, 2 mm,

and 3 mm gaps (Figure 9) show that the bending angle

is inversely proportional to gap size. A 1 mm gap

yields the highest sensitivity (1.62°/kPa) due to strong

inter-chamber interaction, but lower predictability (R²

= 0.973) and complex fabrication. A 3 mm gap

minimizes interaction, giving the lowest sensitivity

(1.22°/kPa) but slightly better predictability (R² =

0.983). The 2 mm gap offers a balance with moderate

sensitivity (1.45°/kPa), highest predictability (R² =

0.987), and ease of manufacturing, thus selected as

optimal.

(a) (b)

(c)

Figure 9: (a) Chamber Gap (b) FEA Simulation (c) Pressure

and Bending Angle variation.

2. Side Wall Thickness

The side wall, i.e, the outer enclosure of each air

chamber, affects actuator flexibility, pressure

resistance, and deformation. FEA simulations for

thicknesses of 1 mm, 2 mm, and 3 mm (Figure 10)

show bending angle is inversely proportional to wall

thickness: thicker walls enhance pressure resistance

but reduce flexibility. At 1 mm, the actuator achieved

the highest bending sensitivity (1.718 °/kPa) but

slightly reduced predictability (R² = 0.997) and a

higher risk of ballooning. At 3 mm, stiffness limited

bending, yielding the lowest sensitivity (1.052 °/kPa)

and predictability (R² = 0.963). The 2 mm wall

provided an optimal balance with moderate

sensitivity (1.412 °/kPa), good predictability (R² =

0.973), and adequate structural stability, making it the

preferred choice.

(a) (b)

(c)

Figure 10: (a) Side Wall (b) FEA Simulation (c) Pressure

and Bending Angle variation.

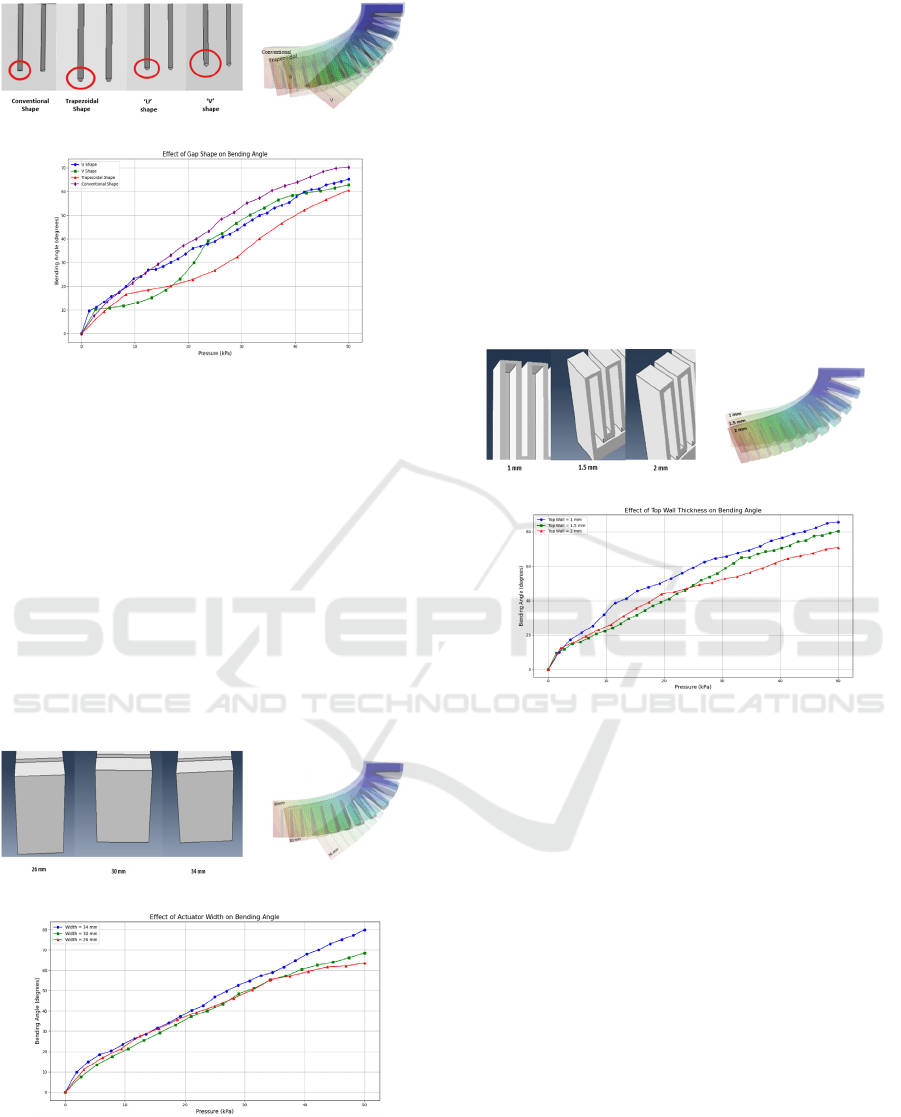
3. Gap Shape

The gap shape, i.e the geometric profile of the space

between adjacent chambers influences deformation

and stress distribution. Four geometries were studied:

rectangular (conventional), trapezoidal, U-shaped, and

V-shaped (Figure 11). The rectangular gap delivered

the highest bending sensitivity (1.41°/kPa) and strong

predictability (R² = 0.973), ensuring consistent

deformation and mechanical efficiency. The U-shape

offered moderate sensitivity (1.08°/kPa, R² = 0.967)

with balanced stress distribution and ease of

fabrication. The V-shape showed slightly lower

sensitivity (1.05°/kPa, R² = 0.963) and risk of localized

stress. The trapezoidal shape minimized stress

concentration but had the lowest sensitivity (1.03°/kPa,

R² = 0.961) and slower actuation. The rectangular gap

was selected for the final design due to its superior

performance and manufacturing simplicity.

4. Width of Actuator (Tapered Profile)

The actuator width, i.e, total lateral dimension at the

base of chambers with a 2° taper based on 3C2

optimization,

affects bending capability, pressure

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

121

(a) (b)

(c)

Figure 11: (a) Gap Shape (b) FEA Simulation (c) Pressure

and Bending Angle variation.

response, and stability. Three widths: 26 mm, 30 mm,

and 34 mm, were tested (Figure 12). The 34 mm

width showed the highest bending sensitivity

(1.41°/kPa, R² = 0.973) but increased material use and

reduced stiffness. The 26 mm width offered higher

stiffness and faster response but slightly lower

sensitivity (1.05°/kPa, R² = 0.963). The 30 mm width

achieved balanced performance (1.08°/kPa, R² =

0.967), combining substantial bending, stability, and

ease of manufacturing. It was selected as optimal,

avoiding the over-deformation of wider profiles while

maintaining high controllability.

(a) (b)

(c)

Figure 12: (a) Width at fixed end (b) FEA Simulation (c)

Pressure and Bending Angle variation.

5. Top Wall Thickness

Top wall thickness i.e material layer sealing each

chamber from above, inversely proportional to

bending angle, influences pressure containment,

bending range, and deformation uniformity. FEA

tests on 1 mm, 1.5 mm, and 2 mm thicknesses (Figure

13) showed that 1 mm yielded the highest sensitivity

(1.52°/kPa, R² = 0.971) but reduced pressure

resistance and increased ballooning risk. The 2 mm

wall was stiffest (1.05°/kPa, R² = 0.963), limiting

bending but improving high-pressure durability. The

1.5 mm thickness provided balanced performance

(1.26°/kPa, R² = 0.969), offering substantial bending

with improved stability, and was selected as optimal.

(a) (b)

(c)

Figure 13: (a) Top wall (b) FEA Simulation (c) Pressure and

Bending Angle variation.

6. Bottom Wall Thickness

Bottom wall thickness defines the actuator’s ability to

resist vertical deformation under internal pressure,

influencing stability and bending performance. FEA

tests on 5 mm, 6 mm, and 7 mm thicknesses show an

inverse relation with bending angle, as in Figure 14.

The 5 mm wall had the highest sensitivity (1.48 °/kPa,

R² = 0.972) but higher bulging risk; the 7 mm wall

was most rigid (1.06 °/kPa, R² = 0.965) but limited

bending. The 6 mm wall offered balanced sensitivity

(1.25 °/kPa, R² = 0.970), good durability, and

manufacturability, making it optimal.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

122

(a) (b)

(c)

Figure 14: (a) Bottom wall (b) FEA Simulation (c) Pressure

and Bending Angle variation.

4 BIO-MIMICRY OF MODIFIED

SOFT ACTUATOR DESIGN

WITH SUCKERS

Biomimicry draws inspiration from nature’s forms,

processes, and systems to inspire engineering

solutions (Benyus 1997). The modified soft actuator

here takes inspiration from the octopus tentacle,

which is a flexible, tapered, boneless structure with

rows of suckers decreasing in size toward the tip. The

suction force generated by a suction cup is given by:

F=ΔP×A

where ΔP is the pressure difference (assumed vacuum

pressure: –50 kPa, atmospheric pressure: 101.3 kPa),

and A=πr

is the effective area. Five suckers were

considered with radii from 5 mm to 9 mm.

A simulation study in Figure 15 shows that adding

more suckers increases total suction force by

enlarging the contact area, but too many suckers

reduce the actuator’s bending angle due to increased

surface stiffness. To balance adhesion with flexible

bending, three suckers were selected, placed at

40 mm, 70 mm, and 100 mm along the actuator, with

diameters of 20 mm, 18 mm, and 16 mm,

respectively. This configuration optimizes surface

contact, sealing, and bending for effective gripping of

spherical or irregular objects as shown in Figure 16.

Figure 15: Simulation for number of suckers.

Figure 16: Suction Force vs Bending Angle vs Number of

Suckers.

(a) (b)

Figure 17: (a) Actuator Sectional View (b) CAD Model for

3C-2 degree with Sucker.

Table 3: Parameters of SPA.

Parameters Value (mm)

Side wall thickness (s) 2

Top wall thickness (t) 1.5

Chamber

ap (a) 2

Bottom la

er (b) 6

Width at base 30

Sucker Diameter (D1) 20

Sucker Diameter (D2) 18

Sucker Diameter (D3) 16

5 SIMULATION STUDIES

The soft actuator was simulated and analysed using

the standard explicit model in ABAQUS/CAE

6.14 (Dassault Systems, 2021) to study the bending

angle under different pressure conditions. The

material parameters used for 3D printing 50A resin

was used in the simulation. The material coefficients

= 0.25 MPa, C

= −0.05 MPa, C

= 0.005 MPa

(Sun et al., 2019), were used for Yeoh hyper elastic

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

123

mathematical model to characterize the nonlinear

stress-strain behaviour of the soft actuator.

Since the actuator undergoes large deformations

with nonlinear effects in simulation, Nlgeom was

activated ‘ON’. The selected mesh type was 3D

stress, 10-node quadratic tetrahedral hybrid elements

(C3D10H).

A mesh convergence study was performed with

varying global mesh sizes (ranging from 1.5 mm to

4.0 mm).

A mesh size of 2.5 mm was selected as it offered

a good balance between simulation accuracy and

computational efficiency, with negligible variation

observed in deformation behavior upon further

refinement as shown in Figure 18.

(a) (b) (c)

Figure 18: (a) Meshing (b) Gravity Load, Internal Pressure,

BC (c) Self Contact Interaction.

6 PROTOTYPING AND TESTING

The soft actuator was fabricated using SLA (Stereo

lithography) 3D printing on a Formlabs Form 3L

printer with Elastic 50A resin, a flexible material

suitable for pneumatic actuation. The process began

with cleaning the build plate, loading the resin tank

and cartridges, and preparing the print file using

PreForm software for optimal orientation and

support. The final prototype is shown in Figure 19.

Figure 19: (a-c) 3D Printing Steps, (d) Final prototype.

The experimental setup, along with a schematic

diagram of the experimental setup, is shown in Figure

20.

(a)

(b)

Figure 20: (a) Experimental Setup (b) Schematic Diagram

for SPA.

6.1 Bending Angle Measurement

Figure 21: Bending angle of the actuator.

Figure 21 explains the methodology adopted for the

bending angle measurement of the multi-chamber

actuator. Figure 22 shows a comparison of the

bending angle for simulation and experiment.

Figure 22: Bending angle wrt Pressure: Comparison of

Simulation and Experimental results.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

124

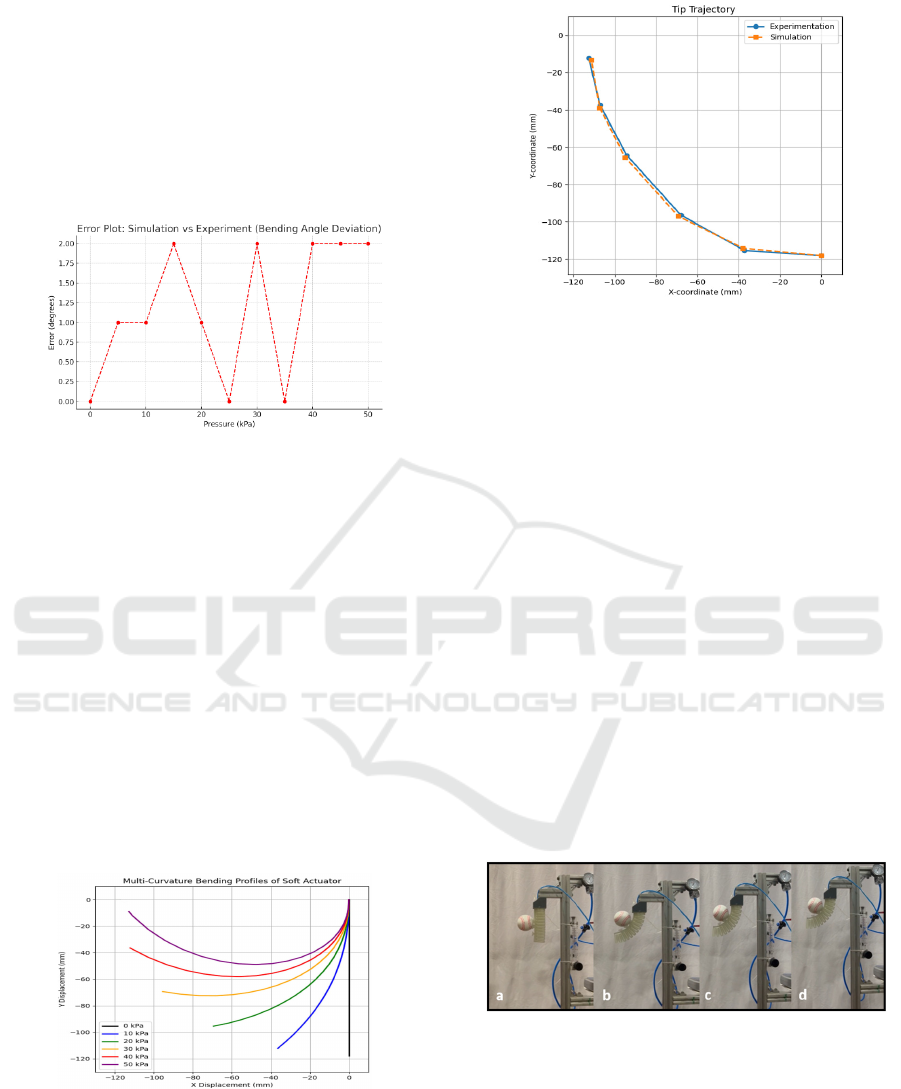
6.2 Error Analysis

To validate accuracy, an error plot of absolute

bending angle deviation between simulation and

experiments shows differences within 2° across the

pressure range, confirming strong agreement as

shown in Figure 23. Minor discrepancies may arise

from material nonlinearity, fabrication tolerances, or

experimental variability.

Figure 23: Bending Error Analysis.

6.3 Multi-Curvature Bending Shape

and Tip Trajectory Analysis

Two deformation analyses were conducted for the

multi-chamber, multi-curvature soft actuator.

Bending profiles were plotted at various pressures

by tracking midline points, revealing non-uniform,

multi-curvature bending shown in Figure 24. This

behavior enhances dexterity and spatial adaptability

in soft robotic tasks.

Tip trajectories were obtained from experimental

video tracking and Abaqus/CAE simulations by

recording X–Y displacements of the actuator tip

relative to the base. The curves show nonlinear tip

motion with pressure, reflecting multi-configuration

deformation shown in Figure 25.

Figure 24: Bending Curve Profiles.

Figure 25: Tip Trajectory.

6.4 Curvature Adaptability Index (CAI)

The CAI measures how effectively an actuator

changes curvature with pressure, which is critical for

adaptable grasping and shape conformity. For the 118

mm multi-chamber, multi-curvature actuator, the

CAI between 10 kPa and 50 kPa is 0.1886

rad·m⁻¹·kPa⁻¹, equivalent to a bending sensitivity of

1.275°/kPa, indicating high curvature responsiveness

and precise deformation control.

7 ACTUATOR GRASPING TEST

The Bending and Gripping capability of the Single

actuator was tested as discussed below.

(a) A small rubber ball was chosen to test the

actuator’s ability to handle compact and delicate

items. The actuator successfully demonstrated its

capability to conform to and grip this ball, as

illustrated in Figure 26.

Figure 26: Demonstration of grasping of a rubber ball.

(b) A smooth, soft plastic ball was used to test the

actuator’s ability to adapt to bigger, lightweight

spherical objects. The actuator reliably grasped

and held this object, as illustrated in Figure 27.

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

125

Table 4: Comparison of Proposed Actuator with Existing Designs from Literature.

Reference Type Curvature Profile Key Features

Gariya et al.,

2023

Single chamber Single Ballooning, limited control

Song et al.,

2021

Multi-chamber with

grouped

Multi

Programmable deformation, improved dexterity, Multi-

channel, Complex pneumatic system

Ansari et al.,

2025

Multi-chamber Multi Low output force, no adhesion

Ansari et al.,

2025 (Proposed)

Multi-chamber Multi

Improved curvature range, integrated adhesion i.e

suction for better grasps adaptability

Figure 27: Demonstration of grasping a plastic ball.

8 COMPARATIVE ANALYSIS

The proposed multi-chamber, multi-curvature soft

pneumatic actuator was compared with recent

literature and a previous in-house prototype (Ansari

et al., 2025), as summarized in Table 4. It shows that

the proposed actuator is superior to the available soft

actuators.

9 CONCLUSIONS AND FUTURE

SCOPE

This work presented a bioinspired multi-chamber,

multi-curvature soft pneumatic actuator with

integrated suction cups, designed for variable bending

curvature and adaptive grasping. Using Yeoh

hyperelastic model and FEA, the design space was

explored through parametric studies on chamber gap,

wall thickness, and taper angle. Tip trajectory and

Bending Curve profile confirms the multi-curvature

effects. The actuator achieved a Curvature

Adaptability Index (CAI) of 0.1886 rad·m⁻¹·kPa⁻¹

and bending sensitivity of 1.275°/kPa for a 118 mm

length, outperforming conventional single-curvature

designs in curvature adaptability and tip deflection.

Future work will address these through

asymmetry metrics for design evaluation, inverse

optimization for predictive modeling, multi-finger

gripper integration, exotic chamber geometries,

embedded sensing, and closed-loop control for

precision grasping, aiming to expand applicability in

industrial and service robotics.

REFERENCES

Ansari, U., Pramod, A. S., Varala, N., & Asokan, T. (2025,

July). Design and analysis of a multi-chamber, multi-

curvature soft pneumatic actuator for controlled

directional bending actuation. In AIR 2025 (to appear).

Ariyanto, M., Mulyanto, D., Munadi, M., Nugroho, T., &

Setiawan, J. D. (2019). Three-fingered soft robotic

gripper based on pneumatic network actuator. In 2019

6th International Conference on Information

Technology, Computer, and Electrical Engineering

(ICITACEE) (pp. 1–6). IEEE.

Benyus, J. M. (1997). Biomimicry: Innovation inspired by

nature. Harper Perennial.

Calisti, M., Giorelli, M., Levy, G., Mazzolai, B., Hochner,

B., Laschi, C., & Dario, P. (2011). An octopus-

bioinspired solution to movement and manipulation for

soft robots. Bioinspiration & Biomimetics, 6(3),

036002.

Dassault Systèmes. (2021). Abaqus/CAE User’s Guide

(Version 2021). Dassault Systèmes Simulia Corp.

Gariya, N., Asrani, A., Kumar, S., & Nautiyal, H. (2023).

Bending mechanics of the soft pneumatic single air

chamber bending actuator.

Gariya, N., Kumar, P., Prasad, B., & Singh, T. (2023). Soft

pneumatic actuator with an embedded flexible

polymeric piezoelectric membrane for sensing bending

deformation. Materials Today Communications, 35,

105910.

Hu, W., Mutlu, R., Li, W., & Alici, G. (2018). A structural

optimisation method for a soft pneumatic actuator.

Robotics, 7(2), 24.

Huang, W., Xiao, J., & Xu, Z. (2021). A variable structure

pneumatic soft robot. Scientific Reports, 11, 1–10.

Lei, J., Ge, Z., Fan, P., Zou, W., Jiang, T., & Dong, L.

(2022). Design and Manufacture of a Flexible

Pneumatic Soft Gripper. Applied Sciences, 12(13),

6306.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

126

Mosadegh, B., Polygerinos, P., Keplinger, C., Wennstedt,

S., Shepherd, R. F., Gupta, U., Shim, J., Bertoldi, K.,

Walsh, C. J., & Whitesides, G. M. (2014). Pneumatic

networks for soft robotics that actuate rapidly.

Advanced Functional Materials, 24(15), 2163–2170

Navas, E., Fernandez, R., Sepúlveda, D., Armada, M., &

Gonzalez-de Santos, P. (2021). Soft grippers for

automatic crop harvesting: A review. Sensors, 21(8),

2689.

Ogden, R. W. (1997). Nonlinear elastic deformations (2nd

ed.). Dover Publications.

Polygerinos, P., Wang, Z., Overvelde, J. T. B., Galloway,

K. C., Wood, R. J., Bertoldi, K., & Walsh, C. J. (2015).

Modeling of soft fiber-reinforced bending actuators.

IEEE Transactions on Robotics, 31(3), 778–789.

Qin, L., Peng, H., Huang, X., Liu, M., & Huang, W. (2023).

Modeling and simulation of dynamics in soft robotics:

A review of numerical approaches. Current Robotics

Reports, 5(1), 1–13.

Rogóż, M., Zeng, H., Xuan, C., Wiersma, D. S., &

Wasylczyk, P. (2016). Soft robotics: Light-driven soft

robot mimics caterpillar locomotion in natural scale.

Advanced Optical Materials, 4(11), 1902–1906.

Singh, K. S., & Asokan, T. (2019, October). Design and

analysis of a soft bidirectional bending actuator for

human-robot interaction applications. In 2019 28th

IEEE International Conference on Robot and Human

Interactive Communication (RO-MAN) (pp. 1–6).

IEEE.

Song, E. J., Lee, J. S., Moon, H., Choi, H. R., & Koo, J. C.

(2021). A multi-curvature, variable stiffness soft

gripper for enhanced grasping operations. Actuators,

10(12), 316.

Su, H., Hou, X., Zhang, X., Qi, W., Cai, S., Xiong, X., &

Guo, J. (2022). Pneumatic soft robots: Challenges and

benefits. Actuators, 11(3), 92.

Sun, Y., Zhang, Q., Chen, X., & Chen, H. (2019). An

optimum design method of Pneu-Net actuators for

trajectory matching utilizing a bending model and GA.

Journal of Robotics, 2019, 6721897.

Tang, X., Li, H., Ma, T., Yang, Y., Luo, J., Wang, H., &

Jiang, P. (2022). A review of soft actuator motion:

Actuation, design, manufacturing and applications.

Actuators, 11(11), 331.

Wu, Y., Yim, J. K., Liang, J., Shao, Z., Qi, M., Zhong, J.,

& Lin, L. (2019). Insect-scale fast-moving and

ultrarobust soft robot. Science Robotics, 4(32),

eaax1594.

Yang, F., Ruan, Q., Man, Y., Xie, Z., Yue, H., Li, B., & Liu,

R. (2020). Design and optimize of a novel segmented

soft pneumatic actuator. IEEE Access, 8, 3006865–

3006877.

Yeoh, O. H. (1993). Some forms of the strain energy

function for rubber. Rubber Chemistry and Technology,

66(5), 754–771.

Zhang, H., Kumar, S., Chen, F., Fuh, J. Y. H., & Wang, M.

Y. (2019). Topology optimized multimaterial soft

fingers for applications on grippers, rehabilitation, and

artificial hands. IEEE/ASME Transactions on

Mechatronics, 24(1), 120–131.

Zhang, J., Wang, T., & Hong, J. (2017). Review of soft-

bodied manipulator.

Journal of Mechanical

Engineering, 53(13), 19–28.

Zaidi, S., Maselli, M., Laschi, C., & Cianchetti, M. (2021).

Actuation technologies for soft robot grippers and

manipulators: A review. Current Robotics Reports,

2(3), 167–181.

Design Space Exploration and Performance Evaluation of a Multi-Chamber, Multi-Curvature Soft Actuator for Robotic Applications

127