Inferring Semantic Schemas on Tabular Data Using Functional
Probabilities
Gin
´
es Almagro-Hern
´
andez
1,2 a
and Jesualdo Tom
´
as Fern
´
andez-Breis
1,2 b
1
Departamento de Inform
´
atica y Sistemas, Universidad de Murcia, CEIR Campus Mare Nostrum, Murcia, Spain
2
IMIB-Pascual Parrilla, Murcia, 30100, Spain
Keywords:
Knowledge Engineering, Schema Inference, Functional Probability.
Abstract:
In the information age, tabular data often lacks explicit semantic metadata, challenging the inference of its
underlying schema. This is a particular challenge when there is no prior information. Existing methodologies
often assume perfect data or require supervised training, which limits their applicability in real-world sce-
narios. The relational database model utilizes functional dependencies (FDs) to support normalization tasks.
However, the direct application of strict FDs to real-world data is problematic due to inconsistencies, errors, or
missing values. Previous proposals, such as fuzzy functional dependencies (FFDs), have shown weaknesses,
including a lack of clear semantics and ambiguous benefits for database design. This article proposes the
concept of functional probability (FP), a novel approach for quantifying the probability of existence of a func-
tional dependency between incomplete and uncertain data, for supporting semantic schema inferencing. FP
measures the probability that a randomly selected tuple satisfies the functional dependency with respect to the
most frequent association observed. Based on Codd’s relational model and Armstrong’s axioms, this method-
ology allows for inferring a minimal and non-redundant set of FDs, filtering weak candidates using probability
thresholds. The method has been evaluated on two tabular datasets, yielding expected results that demonstrate
its applicability. This approach overcomes the limitations of strict dependencies, which are binary, and FFDs,
which lack clear semantics, offering a robust analysis of data quality and the inference of more realistic and
fault-tolerant database structures.
1 INTRODUCTION
Tabular data is pervasive but rarely carries ex-
plicit semantics, hindering automated interpreta-
tion, integration, and transformation into knowledge
graphs—especially under noise and missing values.
The question we aim to answer with our work is,
given only a raw table, how closely an induced se-
mantic schema can approximate the designer’s intent.
Without external ontologies or prior knowledge, we
recover inter-column relations and discover classes,
attributes, and properties directly from the data.
Our core notion is functional probability, p(A →
B), the probability that a functional dependency from
column set A to B holds in the dataset. Unlike clas-
sical FDs (binary) and fuzzy FDs (requiring prede-
fined similarities and thresholds), functional proba-
bility is a graded, data-driven measure that tolerates
noise and incompleteness. Estimating these prob-
a
https://orcid.org/0000-0002-1478-4286
b
https://orcid.org/0000-0002-7558-2880
abilities yields a probabilistic dependency structure
that guides schema induction: identifying candidate
keys, foreign-key–like links, attribute groupings, and
higher-level concepts.
The framework builds on Codd’s FDs and normal-
ization (Codd, 1970) and Armstrong’s axioms (Arm-
strong, 1974). We replace exact with probabilistic sat-
isfaction while retaining Armstrong-style inference
for implications; in the limit p(A→B) = 1, we recover
classical FDs. Normalization principles then drive
decompositions that reduce redundancy and maxi-
mize dependency confidence, producing near-lossless
schemas faithful to the underlying generative struc-
ture.
Related work spans: (i) knowledge-base–driven
annotation and matching (e.g., DBpedia, YAGO)
(Zhang and Balog, 2018); (ii) learning-based methods
requiring supervision or engineered features (Koci
et al., 2018); and (iii) profiling and dependency dis-
covery for uniqueness, inclusion, and deterministic
FDs (Papenbrock et al., 2015). These approaches of-
156
Almagro-Hernández, G. and Fernández-Breis, J. T.
Inferring Semantic Schemas on Tabular Data Using Functional Probabilities.
DOI: 10.5220/0013773000004000
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2025) - Volume 2: KEOD and KMIS, pages
156-163
ISBN: 978-989-758-769-6; ISSN: 2184-3228
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

ten assume clean data, depend on external resources,
or lack principled mechanisms under noise. Fuzzy
FDs relax strictness (Je
ˇ
zkov
´
a et al., 2017) but rely on
domain-specific similarities, are costly to verify, and
risk semantic drift.
By estimating functional probabilities directly
from data—without external ontologies, supervision,
or hand-crafted similarity rules—we construct a prob-
abilistic dependency graph for robust schema extrac-
tion. We infer column roles and relationships, pro-
pose normal-form–guided decompositions, and use
Armstrong-style reasoning to reconcile dependen-
cies. Empirically, this yields resilient inferences un-
der noise and missingness and enables automatic dis-
covery of classes, attributes, and properties in raw
CSVs.
In sum, functional probability offers a princi-
pled, domain-agnostic, and practical basis for seman-
tic schema induction from tabular data, preserving the
spirit of classical database theory while accommodat-
ing real-world imperfections. Allowing us to answer
these two questions: i) Can we extract the seman-
tic schema underlying a tabular dataset based solely
on its data?; ii) Can we compare this with what the
designer of that tabular dataset had theoretically in-
tended?
2 METHODS
2.1 Mathematical Foundations
Functional Dependency. According to Codd’s re-
lational model, let {A
1
,A
2
,...,A
n
} be a finite set of
attributes representing the name of the columns of a
dataset in tabular format, such as the CSV format.
Let {D
1
,D
2
,..., D
n
} be a finite collection of sets of
values called domains. Each of the above attributes
A
i
is associated with one of these domains D
i
, that
is, the values in the column they represent belong to
that domain. An abstract description of the structure
of the above table is made by means of a relational
schema R(A
1
: D
1
,A
2
: D
2
,..., A
n
: D
n
), which name is
R. A relation r(R) where X, Y are descriptors (set of
attributes) of R, since X ,Y ⊆ R, a functional depen-
dency (FD) X → Y is said to exist if, for any pair of
tuples t
1
,t
2
∈ r, it is true that:
t
1
[X] = t
2
[X] ⇒ t
1
[Y ] = t
2
[Y ] (1)
Where t
i
[X] is the projection of the tuple t
i
on the
set of attributes X. This means that the values of the
attributes in X uniquely determine the values in Y.
Armstrong’s Axioms. Armstrong’s axioms pro-
vide a sound and complete set of inference rules for
reasoning about functional dependencies in a rela-
tional schema: every dependency derivable by the ax-
ioms is logically implied (|=), and every logically im-
plied dependency is derivable . Let X,Y,Z be sets of
attributes. The axioms are as follows:
1. Reflexivity (Trivial Dependency): If Y ⊆ X , then
X → Y .
2. Augmentation: If X → Y , then XZ → Y Z for any
set of attributes Z.
3. Transitivity: If X → Y and Y → Z, then X → Z.
In addition to the three primary axioms, the fol-
lowing secondary rules can be derived: i) Union. If
X → Y and X → Z, then X → Y Z; ii) Decomposition.
If X → Y Z, then X → Y and X → Z. iii) Pseudo-
Transitivity: If X → Y and Y Z → W , then XZ → W .
Formal Definitions. Let R be a relation schema and
F a set of functional dependencies (FDs) on R.
• Closure. The closure of F is
F
+
= {X → Y | F |= X → Y }.
– Implication is tested via attribute closure: for
X ⊆ R,
X
+
F
= {A ∈ R | F |= X → A},
computed by iteratively applying the Arm-
strong axioms.
• Equivalence. Two FD sets F and G are equiva-
lent, F ≡ G, iff
F
+
= G
+
(equivalently, F |= G and G |= F ).
• Non-redundancy and canonical (minimal) cover.
F is non-redundant if for every f ∈ F ,
(F \ { f }) ̸|= f .
A canonical cover F
c
for F is an equivalent set
F
c
≡ F such that: (i) each FD has a singleton right-
hand side; (ii) no left-hand side contains extraneous
attributes; (iii) no FD is redundant. It is obtained by
iteratively decomposing right-hand sides, removing
extraneous left-hand-side attributes via attribute clo-
sures, and deleting implied FDs (e.g., Ullman’s algo-
rithm (Ullman, 1988) under the Armstrong axioms).
2.2 Functional Probability
Let R(X,Y ) be a finite relation consisting of N tuples,
representing a tabular dataset (e.g., a CSV file) con-
sidered as a population. Let t = (x,y) ∈ R be a tuple
drawn uniformly at random.
Inferring Semantic Schemas on Tabular Data Using Functional Probabilities
157

We define the functional probability of the de-
pendency X → Y , denoted P
f
(X → Y ), as the proba-
bility that a randomly selected tuple satisfies the func-
tional dependency between X and Y with respect to
the most frequent association observed in the dataset.
Formally:
P
f
(X → Y ) = P y = argmax
y
′
freq(x,y
′
) | (x,y) ∼ R
!
(2)
Alternatively, it can be computed directly from
frequency counts as:
P
f
(X → Y ) =
1
N
∑
x∈Dom(X)
max
y∈Dom(Y )
freq(x,y) (3)
Where:
• freq(x,y) denotes the number of times the pair
(x,y) appears in R,
• Dom(X) and Dom(Y ) denote the domains (dis-
tinct values) of attributes X and Y , respectively,
• N is the total number of tuples in R,
• In the case of a tie in max
y
freq(x,y), any of the
most frequent values may be used.
The functional probability estimates the likeli-
hood that a randomly selected tuple from the dataset
satisfies the most frequently observed functional rela-
tionship between attributes X and Y . In this context:
• P
f
(X → Y ) = 1: indicates that the functional de-
pendency holds exactly with no exceptions.
• 0 < P
f
(X → Y ) < 1: indicates the presence of vi-
olations or ambiguity in the dependency.
• P
f
(X → Y ) ≈ 0: suggests that X does not provide
meaningful information to determine Y .
This measure provides a probabilistic assessment
of how well X determines Y across the dataset, based
on the most frequent values observed for each x ∈
Dom(X).
Assumptions about missing values in the calcula-
tion of the functional probability:
• When there is no value in a cell of an attribute,
this is considered missing value (Nan).
• Any tuple of a descriptor is considered null (Nan)
if there is a missing value in any of the attributes
that compose it.
• Any dupla formed by the tuples of two descriptors
is considered null (Nan), if the tuple of any of the
descriptors is Nan.
• Nan duples do not count in the calculation of the
probability of functional dependence.
2.2.1 Functional Probability Matrix
Given a tabular dataset, we compute the functional
probability for every ordered pair of attributes (X,Y ),
where X acts as the determinant and Y as the depen-
dent attribute. Each value quantifies the empirical
probability that the value of X determines the most
frequent value of Y for each unique value of X in the
dataset.
The computed probabilities are stored in a square
matrix, referred to as the functional probability ma-
trix of the dataset. Each entry M
i, j
in this matrix
corresponds to the functional probability P
f
(X
i
→
X
j
), where rows index the determining attributes and
columns index the determined attributes.
Importantly, this matrix is generally not symmet-
ric, since the functional probability from X
i
to X
j
may
differ from that of X
j
to X
i
, reflecting the directional-
ity of the dependency.
To ensure consistency and numerical stability, all
probability values in the matrix are rounded according
to a predefined level of precision.
2.3 Dependency Quality Ratios
The functional probability P
f
(X → Y ) is computed
using only tuples with non-null values in X ∪Y . Miss-
ingness is handled via the following quality ratios.
Let R be a relation over attributes X (determinant)
and Y (implied). Define:
• n: total tuples
• n
′
: tuples with non-null X ∪Y (used in P
f
)
• n
s
: among the tuples used in P
f
, those that satisfy
X → Y
• n
Y
: tuples with Y ̸= null
• n
X
: tuples with X ̸= null
• n
XY
: tuples with X ̸= null and Y ̸= null
Functional Confidence Ratio
C
f
(X → Y ) =
n
′
n
(4)
Determinant Confidence Degree
D
c
(X → Y ) =
n
s
n
Y
(5)
Null-Implication Ratio
P
null
(X → Y ) =
n
X
− n
XY
n
X
(6)
C
f
measures evidential support; D
c
penalizes both
violations and cases with X null while Y is observed;
P
null
estimates how often non-null X implies missing
Y , informing optionality.
KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development
158

2.4 Semantic Schema Inference System
After computing, for every ordered pair of attributes
in the dataset, a functional probability matrix together
with the corresponding quality ratios, the next step is
to extract a semantically consistent and minimal set
of FDs that summarizes the strongest regularities sup-
ported by the data.
Inference Procedure:
• Candidate Generation and Filtering: Because em-
pirically extracted candidates may be noisy or ap-
proximate, from the functional probability matrix
and quality ratios, we retain X → Y only if the
estimated functional probability P
f
(X → Y ) and
its confidence satisfy user-defined criteria such as
P
f
(X → Y ) ≥ θ with θ ∈ [0,1], where θ = 1 en-
forces exact FDs and smaller values admit approx-
imate ones.
• Logical Consolidation: Use of Armstrong’s ax-
ioms (Armstrong, 1974) via attribute closure tests
to (i) confirm implication relationships between
the candidates and (ii) remove duplicates implied
by stronger dependencies.
• Redundancy elimination: compute a minimal
(canonical) cover F
min
⊆ F
+
, using the Ullman
algorithm (Ullman, 1988) on the filtered set by
eliminating redundant FDs and extraneous at-
tributes on the left-hand side.
The resulting FD set conforms the minimal set of
non-redundant and high-quality functional relation-
ships (F
min
with F
+
min
= F
+
) present in the dataset,
which defines an initial semantic schema that captures
the essential structure and constraints of the data, and
serves as a foundation for further schema design, nor-
malization, or knowledge extraction tasks.
2.5 Evaluation
The evaluation involved applying the developed con-
cepts of functional probability and quality-related ra-
tios on all attribute pairs of two selected Kaggle tab-
ular datasets. These datasets, ”BigBasket Products”
and ”E-Commerce Data”, underwent pre-processing
to remove duplicate rows, handle missing values,
and ensure atomic data, fulfilling the first normal
form (1NF). Subsequently, applying the inference
procedure, the semantic schemes of each dataset
were inferred for the thresholds from 1.0 to 0.90
of the functional probability that produce a change
in the scheme. The obtained schemes were anal-
ysed and compared with the Gold-standard bench-
mark schemes, developed manually by domain ex-
perts. We evaluate alignments using weighted pre-
cision, recall, and F1—rewarding partial matches be-
tween subject–object pairs even if predicates differ,
and coverage measures that penalize extra predicted
classes or properties absent from the gold standard.
These extended metrics complement standard evalu-
ation by providing a more fine-grained assessment of
semantic matching quality.
2.5.1 BigBasket Products
This dataset
1
contains the products listed on the web-
site of online grocery store Big Basket. It consists of
9 columns and 8208 rows. No rows were removed by
our pre-processing. A brief description of the name,
type of data and their values can be found in table 1.
Table 1: BigBasket dataset.
Columns Name Datatypes NoNull Unique
ProductName string 8208 6769
Brand string 8208 842
Price float 8208 1043
DiscountPrice float 8208 2180
Image Url anyURI 8208 8202
Quantity string 8208 781
Category string 8208 11
SubCategory string 8208 334
Absolute Url anyURI 8208 8208
2.5.2 E-Commerce Data
This dataset
2
contains all the transactions occurring
between 01/12/2010 and 09/12/2011 for a UK-based
and registered non-store online retail. This consists
of 8 columns and 541909 initial rows. 530652 rows
remained after our pre-processing. A brief description
of the name, type of data and their values can be found
in Table 2.
Table 2: BigBasket dataset.
Columns Name Datatypes NoNull Unique
InvoiceNo string 530652 25858
StockCode string 530652 3999
Description string 529198 4113
Quantity integer 530652 709
InvoiceDate dataTime 530652 23225
UnitPrice float 530652 1628
CustomerID integer 398005 4370
Country string 530652 38
1
https://www.kaggle.com/dsv/4100336
2
https://www.kaggle.com/datasets/carrie1/
ecommerce-data
Inferring Semantic Schemas on Tabular Data Using Functional Probabilities
159

3 RESULTS
We describe the main results obtained for the two
datasets analyzed.
3.1 BigBasket Products
We evaluated functional probabilities for the Big-
Basket Products dataset (Table 3), finding that
Absolute Url deterministically identifies all other
attributes (probability 1.0), while Image Url ap-
proaches 1.0 for most pairs and ProductName con-
sistently exceeds 0.82. Quality ratios confirm ro-
bustness, functional confidence is 1.0 for all pairs,
the null-implicated ratio is 0, and determinant confi-
dence matches functional probability due to the ab-
sence of missing values. Non-redundant schemas
induced across thresholds 1.0–0.93 (Figure 1) indi-
cate the most coherent structure at θ = 0.98, where
Absolute Url acts as a root (akin to a SalesArti-
cle) determining image, quantity, price, and discount,
and ProductName leads to Brand and Subcategory,
which connects to Category. Quantitatively, θ =
0.98 yields the best gold-standard alignment with
F
1
= 0.625 (Precision = 0.682, Recall = 0.577), ty-
ing the highest global cover (0.684) and class/relation
cover (0.600/0.500) while matching datatype cover
(0.800); this surpasses θ = 0.99 (F
1
= 0.542), θ =
0.93 (F
1
= 0.538), and θ = 1.0 (F
1
= 0.440). Compar-
ison with the expert-crafted gold schema (Figure 2;
(Almagro-Hern
´
andez et al., 2025)) shows strong con-
cordance: Although the method does not group
Price with DiscountPrice, it does associate both
with the SalesArticle class. However it does group
ProductName with Brand, and SubCategory with
Category recovering key associations without exter-
nal ontologies. A current limitation is the inability
to infer subclass relations (e.g., bbp:SubCategory ⊆
bbp:Category), as the approach focuses on column-
level dependencies rather than hierarchical abstrac-
tion. Despite expert subjectivity, the observed align-
ment supports the utility of the functional-probability
framework for schema understanding and semantic
enrichment in the absence of annotations. In addition
to determining the most appropriate instance granu-
larity, as in the case of the ‘Product’ class, which sets
it at the ProductName column level only, while in the
Gold Standard it is set as the union of the values be-
tween the ProductName and Brand columns.
3.2 E-Commerce Data
The functional-dependency probability matrix for
all unary attribute pairs (Table 4) shows no
globally dominant determinant, indicating a dis-
tributed schema; nonetheless, high P
f
(FD) val-
ues arise for InvoiceNo–CustomerID, InvoiceNo–
Country, InvoiceNo–InvoiceDate, InvoiceDate–
Country, CustomerID–Country, and StockCode–
Description, forming localized clusters consistent
with invoices, customers, and products. Qual-
ity ratios are mostly 1.0, except where missing-
ness limits confidence—most notably CustomerID
(∼25% nulls, capping attainable confidence at 0.75)
and Description (null-implication ≈ 0.3%), for
which determinant confidence can fall below P
f
(FD).
Non-redundant schemas generated across thresholds
1.0–0.91 (Figure 3) reveal that θ = 0.96 best matches
intrinsic semantics: InvoiceNo anchors an Invoice
(date, customer), StockCode a Product (description),
and CustomerID a Customer (country); however,
Quantity and UnitPrice remain isolated and no In-
voice–Product link appears due to the unary restric-
tion, which also prevents identifying composite keys
(e.g., InvoiceNo+StockCode). At θ = 0.91 the graph
becomes fully connected but admits spurious links
(e.g., Quantity/UnitPrice to Country), evidencing
a coverage–precision trade-off. Quantitatively, θ =
0.96 yields the best gold-standard fit: highest F
1
=
0.650 and precision 0.929 at recall 0.500 (vs. θ ∈
{1.0,0.99, 0.91} with F
1
= {0.411,0.546,0.520}),
with balanced coverage (class 0.50, datatype 0.75,
global 0.526) while avoiding the false positives ad-
mitted at θ = 0.91 despite its larger global cover
0.571. The inferred structure partially aligns with the
expert conceptual model (Almagro-Hern
´
andez et al.,
2025) (Figure 4) e.g. StockCode→Description,
InvoiceNo→{InvoiceDate, CustomerID}, despite
using no metadata, underscoring robustness to noise
and incompleteness; remaining limitations include
the inability to recover composite relations and to dis-
ambiguate whether dependents (e.g., Country) de-
note foreign keys versus properties, motivating mul-
tivariate/contextual extensions. For all thresholds ex-
cept θ = 0.99, the identifiers of the inferred classes are
obtained in accordance with those of the gold stan-
dard. This again indicates that this method is also
suitable for this function.
4 DISCUSSION
The experiments conducted on two structurally dis-
tinct datasets demonstrate the practical value of mod-
eling functional dependencies probabilistically. By
computing a functional dependency probability for all
pairs of attributes, and supplementing this with min-
imum and maximum confidence intervals as well as
KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development
160

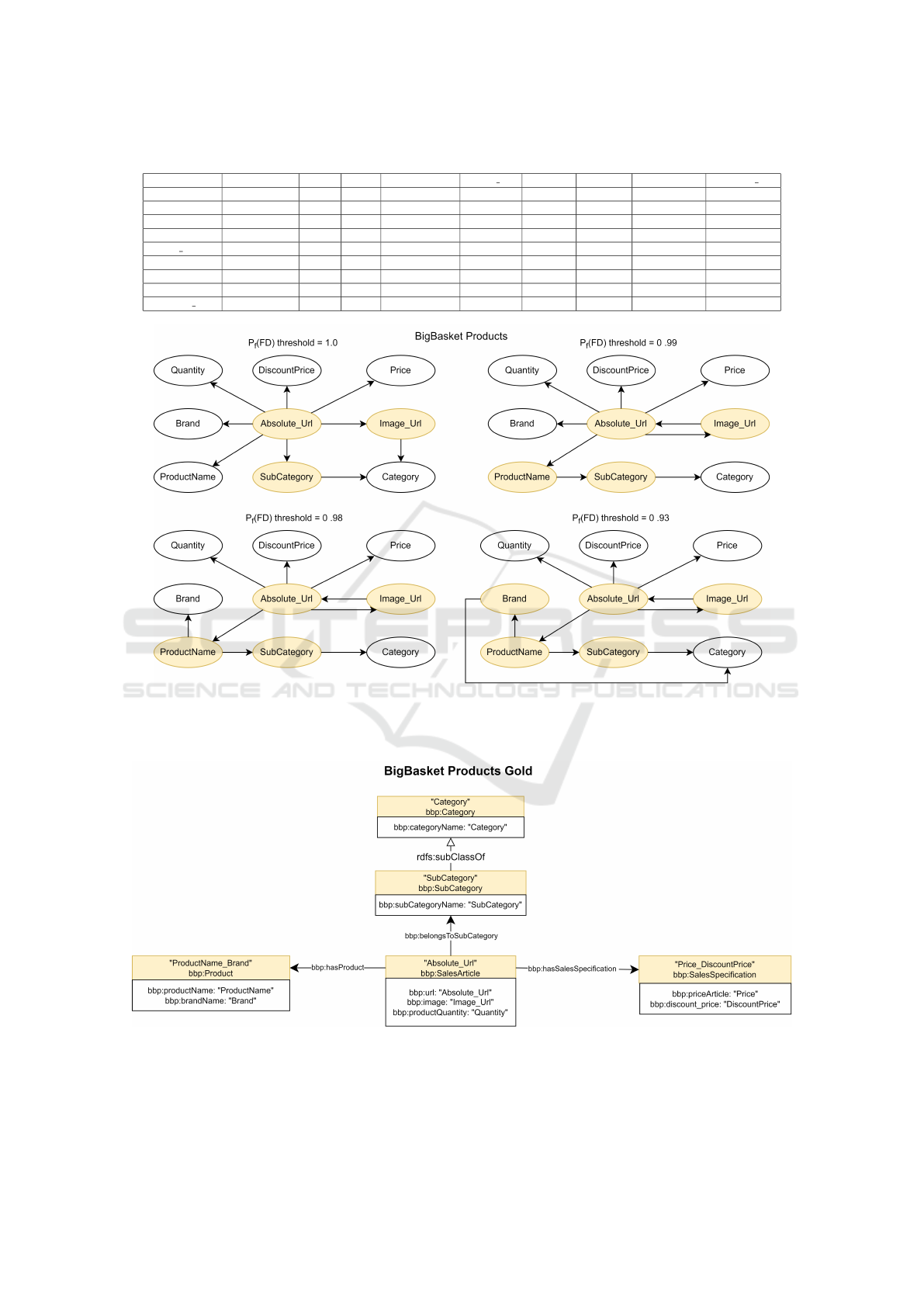
Table 3: Functional probability for the BigBasket dataset. An accuracy of 3 decimal numbers has been used.
ProductName Brand Price DiscountPrice Image Url Quantity Category SubCategory Absolute Url
ProductName 1.0 0.988 0.835 0.833 0.825 0.842 0.999 0.995 0.825
Brand 0.156 1.0 0.226 0.208 0.103 0.372 0.93 0.58 0.103
Price 0.134 0.28 1.0 0.319 0.127 0.291 0.604 0.291 0.127
DiscountPrice 0.272 0.441 0.591 1.0 0.266 0.46 0.696 0.432 0.266
Image Url 0.999 0.999 0.999 0.999 1.0 0.999 1.0 0.999 0.999
Quantity 0.106 0.304 0.193 0.171 0.095 1.0 0.667 0.348 0.095
Category 0.008 0.163 0.037 0.027 0.002 0.166 1.0 0.175 0.001
SubCategory 0.091 0.386 0.127 0.117 0.041 0.315 1.0 1.0 0.041
Absolute Url 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
Figure 1: Schemes inferred from the functional probability matrix, for the BigBasket dataset, according to the conditional
probability thresholds 1.0, 0.99, 0.98 and 0.93. The coloured node indicates that this is a determinant, in one of the functional
dependencies depicted.
Figure 2: Gold standard semantic schema manually derived by a domain expert for the BigBasket Products dataset. This
schema represents the reference relationships between attributes, used to evaluate the quality of automatically inferred seman-
tic structures.
Inferring Semantic Schemas on Tabular Data Using Functional Probabilities
161

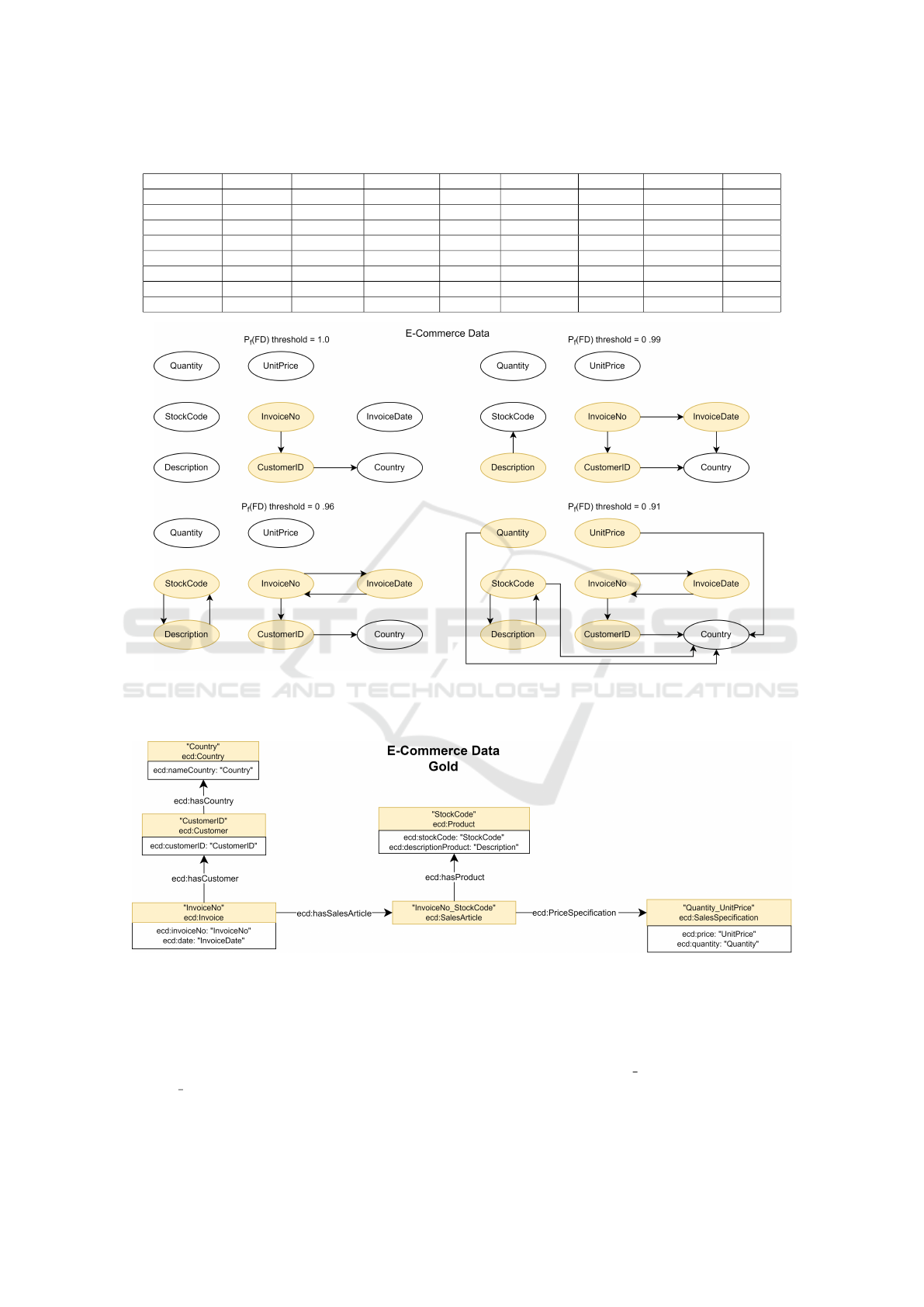
Table 4: Functional probability for the E-Commerce dataset. An accuracy of 3 decimal places has been used.
InvoiceNo StockCode Description Quantity InvoiceDate UnitPrice CustomerID Country
InvoiceNo 1.0 0.053 0.051 0.446 0.999 0.227 1.0 1.0
StockCode 0.011 1.0 0.986 0.379 0.011 0.692 0.051 0.914
Description 0.011 0.995 1.0 0.380 0.012 0.692 0.052 0.914
Quantity 0.005 0.018 0.018 1.0 0.005 0.144 0.035 0.913
InvoiceDate 0.963 0.049 0.047 0.437 1.0 0.220 0.965 0.994
UnitPrice 0.009 0.076 0.075 0.351 0.009 1.0 0.039 0.914
CustomerID 0.341 0.034 0.033 0.332 0.341 0.169 1.0 1.0
Country 0.008 0.007 0.007 0.285 0.008 0.094 0.057 1.0
Figure 3: Schemes inferred from the functional probability matrix, for the E-Commerce dataset, according to the conditional
probability thresholds 1.0, 0.99, 0.96 and 0.91. The coloured node indicates that this is a determinant, in one of the functional
dependencies depicted.
Figure 4: Gold standard semantic schema manually derived by a domain expert for the E-commerce Data dataset. This schema
represents the reference relationships between attributes, used to evaluate the quality of automatically inferred semantic struc-
tures.
quality ratios, we obtained a fine-grained view of the
dependency landscape inherent to each dataset.
In the BigBasket dataset, the attribute
Absolute Url emerges as a strong global deter-
minant with P
f
(FD) = 1.0 for all other attributes.
This behavior clearly identifies it as a surrogate
key and structural root of the data schema. Other
attributes such as Image Url and ProductName also
exhibit high dependency probabilities, reinforcing
their roles as identifiers and descriptors of product en-
KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development
162

tities. The non-redundant schemas derived from this
dataset—particularly at a threshold of 0.98—reveal
coherent semantic structures that mirror typical onto-
logical hierarchies (e.g., from product name to brand,
subcategory, and category). Among the evaluated
cutoffs, θ = 0.98 shows the strongest alignment with
the gold standard by optimizing the precision–recall
trade-off, maximizing agreement across axiom types,
and preserving a compact schema; stricter thresholds
underfit key concepts, whereas looser ones inflate the
axiom set without improving fidelity.
In contrast, the E-commerce Transactions dataset
displays a more fragmented structure, where no single
attribute universally determines the others. However,
clusters of strong dependencies (e.g., InvoiceNo →
CustomerID, StockCode → Description) suggest
the presence of localized semantic groupings such
as invoice, customer, and product entities. Despite
this, non-redundant schemas extracted from the de-
pendency matrix reveal limitations: at stricter thresh-
olds, key entities are isolated, while at looser thresh-
olds, semantically implausible dependencies emerge.
This highlights a central trade-off between seman-
tic precision and schema completeness when deter-
mining thresholds for dependency extraction. Within
this trade-off, a threshold of 0.96 best aligns with
the gold standard, recovering the core classes and
datatype properties with minimal noise—improving
completeness over tighter cutoffs (1.0, 0.99) while
avoiding the spurious links that appear at looser set-
tings (θ = 0.91).
The analysis of quality ratios confirms the impor-
tance of data completeness: missing values notably
reduce the interpretability and confidence of discov-
ered dependencies.
Our approach (i) provides a smooth and quantita-
tive spectrum for assessing how close a relationship
is to being functionally deterministic; ii) it supports
practical applications in data quality assessment, nor-
malization design, and error detection in tabular data;
iii) it also allows the granularity of instances to be de-
termined for each inferred class. Further work will
focus on the modeling of hierarchical attributes, cal-
culating multivariate dependencies, considering re-
lationships between multiple attributes and a score-
based schema selection.
5 CONCLUSIONS
This study presents a probabilistic framework for
modeling functional dependencies in tabular datasets.
Our approach is able to capture varying degrees of
functional association through the functional depen-
dency probability matrix, complemented by quality
ratios. This enables the identification of semantically
meaningful structures, even in the presence of noisy
or incomplete data, and facilitates the construction of
non-redundant schemas that align with intrinsic data
semantics.
DATA AVAILABILITY
The data generated in this work is available in our
GitHub repository
3
.
ACKNOWLEDGEMENTS
This research has been funded by MI-
CIU/AEI/10.13039/501100011033/ [grant numbers
PID2020-113723RB-C22, PID2024-155257OB-I00].
REFERENCES
Almagro-Hern
´
andez, G., Mulero-Hern
´
andez, J., Desh-
mukh, P., Bernab
´
e-D
´
ıaz, J. A., S
´
anchez-Fern
´
andez,
J. L., Espinoza-Arias, P., Mueller, J., and Fern
´
andez-
Breis, J. T. (2025). Evaluation of alignment meth-
ods to support the assessment of similarity between e-
commerce knowledge graphs. Knowledge-Based Sys-
tems, 315:113283.
Armstrong, W. W. (1974). Dependency structures of data
base relationships. In IFIP Congress.
Codd, E. F. (1970). A relational model of data for large
shared data banks. Commun. ACM, 13(6):377–387.
Je
ˇ
zkov
´
a, J., Cordero, P., and Enciso, M. (2017). Fuzzy func-
tional dependencies: A comparative survey. Fuzzy
Sets and Systems, 317:88–120. Theme: Logic and
Computer Science.
Koci, E., Neumaier, S., and Umbrich, J. (2018). A machine
learning approach for interlinking tabular data. In The
Semantic Web: ESWC 2018, volume 10843 of Lecture
Notes in Computer Science, pages 307–322. Springer.
Papenbrock, T., Ehrlich, J., Marten, J., Neubert, T.,
Rudolph, J.-P., Sch
¨
onberg, M., Zwiener, J., and Nau-
mann, F. (2015). Functional dependency discovery:
An experimental evaluation of seven algorithms. Pro-
ceedings of the VLDB Endowment, 8(10):1082–1093.
Presented at the 41st International Conference on Very
Large Data Bases (VLDB), 2015.
Ullman, J. D. (1988). Principles of Database and
Knowledge-Base Systems, Vol. I. Computer Science
Press, Rockville, MD.
Zhang, S. and Balog, K. (2018). Ad hoc table retrieval using
semantic similarity. In Proceedings of the 2018 World
Wide Web Conference on World Wide Web - WWW ’18,
WWW ’18, page 1553–1562. ACM Press.
3
https://github.com/gines-almagro/
Inferring-Semantic-Schemas-from-Functional-Probabilities
Inferring Semantic Schemas on Tabular Data Using Functional Probabilities
163