
Manipulability Maximization of a Liquid-Handling Manipulator for
Sloshing Suppression via Container Tilting
Ryuji Nakagawa
a
and Ryosuke Tasaki
b
Department of Mechanical Engineering, Aoyama Gakuin University, Sagamihara, Kanagawa, Japan
Keywords: Manipulability, Sloshing Suppression, Optimization Problem, Trajectory Constraint.
Abstract: The manipulability index measures a robot’s motion capability. To avoid singularity problems and to achieve
unexpected changes in tasks, a method that explicitly considers this metric is needed. However, the index is
a nonlinear function that depends on the state of the manipulator, making optimization difficult in a short
period of time. In addition, real-time control of the robot, which requires computational efficiency, is
necessary to ensure safety in a dynamic environment. Previous studies have generated trajectories that
increase this metric, but different tasks require different constraints to be considered. Controlling not only the
trajectory but also the posture and velocity of the end-effector expands the area of practical use. In this paper,
we formulate a manipulability optimization problem for real-time control in liquid transfer and solve it
efficiently using inequality constraints. In liquid transfer experiments, the method successfully generates safe
and kinematic trajectories with high performance by optimizing both manipulability and controlling velocity
and attitude to suppress liquid surface vibration.
1 INTRODUCTION
Recent advances in collaborative robots have
responded to the shift from high-volume to high-mix
production, with increasing demand driven by their
flexibility in adapting to complex tasks (Kavraki et
al., 1996). Unlike industrial robots, collaborative
robots operate safely alongside humans without
traditional safety barriers. In Human-Robot
Collaboration (HRC) spaces, safety remains a
primary concern. Various motion planning
approaches, including RRT and CHOMP, address
collision avoidance and task constraints (LaValle &
Kuffner, 2001; Wang et al., 2019). However,
dynamic environments demand that robots rapidly
adapt to unpredictable situations, requiring
trajectories that maintain high kinematic
performance. The manipulator’s posture critically
affects adaptability (Haowen et al., 2024); poor
configurations limit responsive movements.
The manipulability ellipsoid (Yoshikawa, 1985)
describes the robot’s directional motion capability, and
the manipulability index—proportional to ellipsoid
volume—assesses proximity to singularities.
a
https://orcid.org/0009-0001-0525-5729
b
https://orcid.org/0000-0002-3619-4498
Maximizing this index enhances adaptability in
dynamic environments. Dufour et al. integrated a
linearized manipulability index into inverse kinematics
using Quadratic Programming (2020). Other methods,
such as Gaussian process regression for trajectory
optimization (Maric et al., 2019) and neural networks
(Jin et al., 2017), have also been proposed. More
recently, manipulability optimization has been applied
to multi-arm coordination (Kennel-Maushart et al.,
2021) and human–robot collaboration tasks (Zhang,
2022). However, most studies address manipulability
improvement or task-specific constraints separately,
and few have integrated them into a unified
framework.
In parallel, liquid transfer with open containers is
another challenging problem, where sloshing
suppression has been studied through trajectory
shaping and container tilting strategies (Yano &
Terashima, 2001; Moriello et al., 2018; Muchacho et
al., 2022). These methods effectively reduce liquid
oscillations but generally ignore the kinematic
performance of the manipulator, limiting their
applicability in tasks that require both stability and
adaptability.
350
Nakagawa, R. and Tasaki, R.
Manipulability Maximization of a Liquid-Handling Manipulator for Sloshing Suppression via Container Tilting.
DOI: 10.5220/0013759200003982
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 350-356
ISBN: 978-989-758-770-2; ISSN: 2184-2809
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

Figure 1: Schematic of sloshing suppression control.
This study proposes a trajectory optimization
framework that maximizes the manipulability index
while simultaneously suppressing liquid vibrations. A
key feature of the formulation is that sloshing
suppression is expressed as an inequality constraint
rather than as part of the objective function. This
keeps the objective lightweight and computationally
efficient, while the introduction of flexible constraints
allows the feasible range to be adaptively adjusted,
reducing computational load without sacrificing task
feasibility. These characteristics make the approach
suitable for real-time implementation in dynamic
environments. Effectiveness is validated through
experiments with a 7-DOF manipulator performing
liquid transfer tasks, confirming that the proposed
method achieves safe and kinematically efficient
trajectories that enhance manipulability while
suppressing sloshing.
2 PRINCIPLE OF SLOSHING
SUPPRESSION
Sloshing suppression during liquid transfer has been
extensively studied, with approaches including CFD-
based modeling (Muller et al., 2003; Diavareshkian &
Khalili, 2006) and filtered trajectory generation
targeting vibration frequencies (Yano et al., 2001;
Yano & Terashima, 2001). These typically assume
horizontal container orientation in linear systems. In
contrast, manipulator-based studies explore container
tilting to counteract acceleration-induced liquid
motion (Moriello et al., 2018; Muchacho et al., 2022).
This study proposes a trajectory optimization
method that dynamically adjusts container orientation
based on acceleration while enhancing the
manipulability index. The vibration control strategy
is detailed in this chapter.
2.1 Statement of Tilting Method
Figure 1 illustrates the schematic of the proposed
sloshing suppression control method. Vibration is
mitigated by minimizing horizontal acceleration
within the container, achieved by aligning the
container’s orientation with the direction of the
applied acceleration. The container’s tilt angle 𝜃
[rad] is calculated based on the horizontal
accelerations 𝛼
and 𝛼
[m/s²], the vertical
acceleration 𝛼
[m/s²], and gravitational acceleration
𝑔 [m/s²].
𝜃=tan
𝛼
+𝛼
(
𝑔+𝛼
)
(
1
)
In essence, sloshing is suppressed when the net
acceleration vector acting on the liquid aligns with the
normal vector of the liquid surface.
2.2 Acceleration Smoothing
As shown in (1), the manipulator adjusts the
container’s tilt in response to acceleration. However,
abrupt changes in acceleration, such as step inputs,
can result in infeasible motion due to excessive speed
requirements. To ensure feasibility, the acceleration
profile must be smooth. By regulating the rate of
change of acceleration, the manipulator generates
motion within its operational limits.
The rate of change of acceleration is referred to as
jerk. A low-jerk trajectory ensures smooth
acceleration, enabling the desired tilt of the container.
Accordingly, the optimal trajectory is obtained by
minimizing jerk, as defined by the evaluation
function below, where 𝑥(𝑡) denotes position.
𝐽(𝑥
(
𝑡
)
)=
𝑑
𝑥
(
𝑡
)
𝑑𝑡
𝑑𝑡
(
2
)
The functional reaches its extremum when 𝑥(𝑡)
satisfies the Euler–Poisson equation, allowing the
trajectory to be expressed as a fifth-order polynomial.
𝑥
(
𝑇
)
=𝑥
+𝑥
−𝑥
(
6𝑇
−15𝑇
+10𝑇
)
−𝑣
(
3𝑇
−8𝑇
+6𝑇
−𝑇
)
−𝑣
(
3𝑇
−7𝑇
+4𝑇
)
(3)
−0.5𝑎
(
𝑇
−3𝑇
+3𝑇
−𝑇
)
+0.5𝑎
(
𝑇
−2𝑇
+𝑇
)
𝑇=
𝑡
𝑡
(4)
:
Horizontal acceleration
: Vertical acceleration
Gravity
Liquid surface
Manipulability Maximization of a Liquid-Handling Manipulator for Sloshing Suppression via Container Tilting
351

where 𝑥, 𝑣, and 𝑎 represent the position, velocity,
and acceleration, respectively, while the subscripts 0
and 𝑓 denote the starting and ending points. Equation
(4) is scaled by the final time 𝑡
. This is known as the
minimum jerk model (Flash & Hogan, 1985), which
generates a trajectory with minimal jerk based on the
current state and the endpoint state. In this study, the
trajectory generated using this model is referred to as
the minimum jerk trajectory. When the container is
transported along a smooth acceleration, the lateral
acceleration of the liquid is cancelled by tilting the
container.
3 MANIPULATOR KINEMATICS
AND MANIPULABILITY
Manipulator kinematics consists of forward
kinematics, which computes the end-effector pose
from joint angles, and inverse kinematics, which
determines joint configurations for a desired task-
space pose. The manipulability index, derived from
the Jacobian, reflects the manipulator’s motion
capability.
3.1 Kinematics and Manipulability
The forward kinematics of a manipulator with 𝑛
degrees of freedom at joint configuration 𝑞∈ℝ
is
expressed as
𝑥=𝑓
(
𝑞
)(
5
)
where 𝑥∈ℝ
is the end-effector pose (position and
orientation in task space) and 𝑓
(
∙
)
is a nonlinear
mapping. Since solving this relation directly is often
computationally demanding, it is commonly
linearized through differential kinematics:
𝑥 =𝐽
(
𝑞
)
𝑞
(
6
)
where 𝑥 =
𝑣
𝜔
∈ℝ
represents the linear
velocity 𝑣 and angular velocity 𝜔 of the end-effector,
and 𝑞 is the joint velocity vector. The Jacobian matrix
𝐽
(
𝑞
)
∈ℝ
×
maps joint velocities to task-space
velocities. In this context, 𝐽
(
𝑞
)
represents the
manipulator Jacobian, distinct from the cost
functional 𝐽(𝑥
(
𝑡
)
) defined in (2).
Manipulability is an important index in motion
planning, and increasing it allows for greater
flexibility in motion and avoidance of singularities.
This index is defined as follows
𝑚(𝑞)=
𝑑𝑒𝑡
(
𝐽(𝑞)𝐽(𝑞)
)
=𝜎
(
7
)
where 𝜎
are the singular values of 𝐽(𝑞). Since 𝜎
>
0, 𝑚(𝑞)>0. If 𝑚(𝑞) is close to 0, the manipulator is
close to a singular configuration. Conversely, larger
values correspond to configurations that allow greater
dexterity and adaptability.
3.2 Manipulability Optimization
Optimization-based motion planning enables robots
to generate efficient and safe trajectories under task-
specific constraints. In manipulability optimization,
the objective is to maximize 𝑚(𝑞) , thereby
enhancing motion flexibility and avoiding
singularities. The problem is formulated as:
min
𝑚
(
𝑞
)(
8
)
Subject to
𝑥 =𝐽
(
𝑞
)
𝑞
𝑞
≤𝑞≤𝑞
𝑞
≤𝑞 ≤𝑞
where 𝑞
and 𝑞
are the upper and lower limits of the
joint angle, and 𝑞
and 𝑞
are the joint velocity
limits. Maximizing 𝑚(𝑞) is crucial for generating
trajectories that exhibit high motion performance,
enhancing the overall agility and efficiency of the
manipulator.
The gradient of the manipulability index is
required for iterative optimization. In this study, the
gradient is computed numerically using finite
differences:
∇𝑚
=
𝜕𝑚
(
𝑞
)
𝜕𝑞
=
𝑚
(
𝑞+𝑑𝑒
)
−𝑚
(
𝑞
)
𝑑
(
9
)
where ∇𝑚
is the 𝑖-th element of vector ∇𝑚, and 𝑑 is
a small positive constant. 𝑒
is the unit vector in the
direction of the 𝑖-th joint.
4 MANIPULABILITY
OPTIMIZATION FOR LIQUID
TRANSFERRING TASK
This section proposes a method to optimize
manipulability during liquid transfer by formulating
motion planning as an optimization problem,
incorporating the minimum jerk trajectory as a
constraint.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
352
4.1 Minimum Jerk Trajectory
Constraint
To suppress sloshing during liquid transfer, it is
essential to generate smooth accelerations that do not
excite liquid oscillations. For this purpose, the
minimum jerk trajectory model is adopted as a
constraint in the manipulability optimization
problem. The minimum jerk model provides an
analytic trajectory with minimized jerk, defined by
the third derivative of position, and can be expressed
in polynomial form using the start and end conditions
of the motion.
The general expression of a minimum jerk
trajectory between initial state (𝑥
,𝑣
,𝑎
) and final
state 𝑥
,𝑣
,𝑎
is given by
𝑥(𝑡) = 𝑓(𝑥
,𝑥
,𝑣
,𝑣
,𝑎
,𝑎
,𝑡,𝑡
)
(
10
)
where 𝑡
is the final time. This trajectory guarantees
smooth position, velocity, and acceleration profiles.
In practical liquid transfer tasks, the final velocity and
acceleration are often set to zero (𝑣
= 0, 𝑎
= 0),
which simplifies the formulation.
For real-time implementation, it is convenient to
express the trajectory in recursive form. The position
at the next step is computed from the current state
(𝑥(𝑡),𝑣(𝑡),𝑎(𝑡)) and the target endpoint 𝑥
as
𝑥(𝑡+∆𝑡)= 𝑓(𝑥
,𝑥(𝑡),𝑣(𝑡),𝑎(𝑡),𝑇′)
(
11
)
where ∆𝑡 is the control interval and 𝑇
=∆𝑡𝑡
−𝑡
⁄
represents the normalized time increment. This
recursive formulation allows the trajectory to be
updated at each control step, making it suitable for
online optimization.
In the proposed framework, the minimum jerk
trajectory is not treated as an additional objective, but
rather as an inequality constraint on feasible motions:
𝑥
≤𝑥 ≤𝑥
(
12
)
where the bounds 𝑥
,𝑥
are derived from the
minimum jerk trajectory. To account for the trade-off
between manipulability and trajectory tracking, a
deviation parameter 𝜁 and a scaling function 𝛼(𝑡) are
introduced:
𝑣
±
=𝑓
𝑥
±𝜁𝛼,𝑥
(
𝑡
)
,𝑣
(
𝑡
)
,𝑎
(
𝑡
)
,𝑇
(
13
)
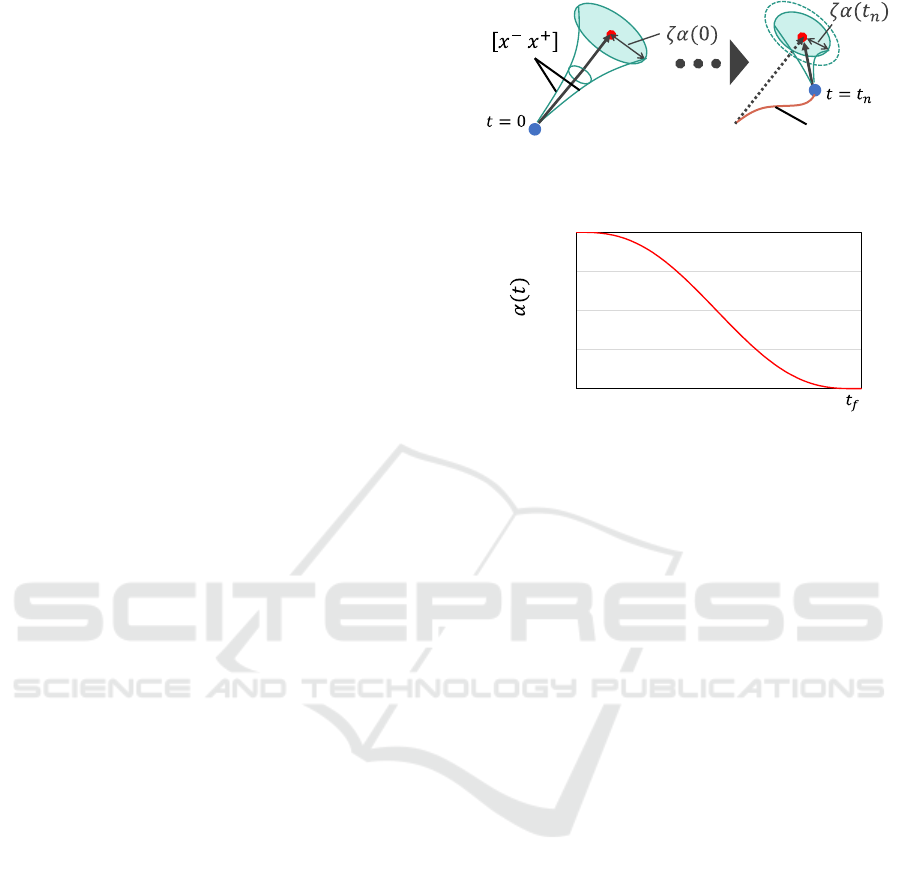
(a) Feasible search region defined by deviation parameter
𝜁 and scaling coefficient 𝛼(𝑡).
(b) Time profile of scaling coefficient 𝛼(𝑡).
Figure 2: Concept of minimum jerk trajectory constraint.
Here, 𝜁≥0 represents the maximum allowable
deviation from the nominal trajectory, while 𝛼(𝑡) is a
time-varying coefficient that gradually decreases
from 1 at the start of the motion to 0 at the end. This
flexible constraint design enlarges the search space at
the beginning of the motion and tightens it near the
goal, thereby reducing computational load while
ensuring convergence to the target. In this
formulation, 𝑣 represents the linear velocity subject
to inequality constraints, while the angular velocity 𝜔
is determined to satisfy the tilting condition in (1) at
every step. Thus, the container orientation is
continuously adjusted to align with the resultant
acceleration vector, ensuring sloshing suppression
during the transfer. Moreover, any sudden change in
deviation must be gradual, as it may lead to abrupt
shifts in the search range. Based on these conditions,
𝛼 was also derived using the minimum jerk model,
along with the trajectory. Figure 2 illustrates this
concept: (a) the feasible region defined by the flexible
constraint shrinks as the task approaches completion;
(b) the scaling coefficient 𝛼(𝑡) decreases smoothly
from 1 to 0 according to the minimum jerk model.
Combining these elements, the constraints of the
optimization problem for liquid transfer can be
expressed as:
𝑥 =𝐽
(
𝑞
)
𝑞
𝑞
≤𝑞≤𝑞
𝑞
≤𝑞 ≤𝑞
𝑥
≤𝑥 ≤𝑥
Start
Goal
Generated path
Range
0
0.25
0.5
0.75
1
Time
0
Manipulability Maximization of a Liquid-Handling Manipulator for Sloshing Suppression via Container Tilting
353
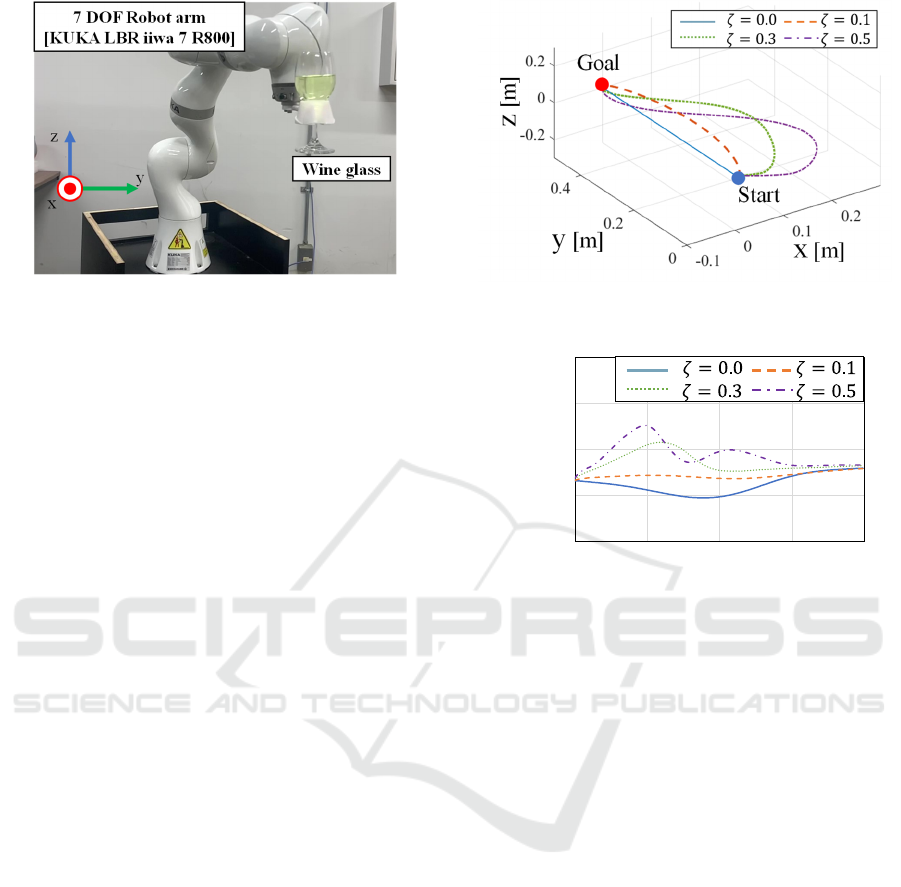
Figure 3: Experimental setup.
with
𝑥
±
=
𝑣
±
𝜔
±
𝑣
±
=𝑓
𝑥
±𝜁𝛼,𝑥
(
𝑡
)
,𝑣
(
𝑡
)
,𝑎
(
𝑡
)
,𝑇
By embedding the minimum jerk model as a
constraint rather than as part of the cost function, the
optimization remains computationally lightweight.
This design is essential for real-time liquid transfer,
where both manipulability enhancement and sloshing
suppression must be achieved simultaneously.
4.2 Experimental Results
To validate the proposed method, liquid transfer
experiments use a KUKA LBR iiwa 7 R800 (7 DOF).
The setup is shown in Figure 3. A wine glass was
transported from the origin (0, 0, 0) to a position
0.5 m along the y-axis within 2.0 s. Trajectory and
manipulability were evaluated for various values of
𝜁, representing the maximum deviation. The case
with 𝜁 = 0, where manipulability is not considered, is
defined as the reference trajectory.
In this study, proposed method is evaluated under
two conditions: Scenario A, a reference trajectory
with high manipulability, and Scenario B, a reference
trajectory with low manipulability that passes near a
singularity.
4.2.1 Scenario A: High Manipulability
Trajectory
Figure 4 shows the transport trajectories, while Figure
5 presents the corresponding manipulability,
normalized by the robot’s maximum value. As 𝜁
increases, trajectory deviation becomes more
pronounced. At 𝜁 = 0, the trajectory is a straight line,
reflecting the minimum jerk model without
manipulability optimization.
Figure 4: Liquid transferring trajectory (Scenario A).
Figure 5: Scaled manipulability (Scenario A).
Figure 5 indicates that the proposed method
maintains high manipulability across all conditions.
The reference trajectory ( 𝜁 = 0) results in lower
manipulability, suggesting limited kinematic
performance and potential instability near
singularities. In contrast, optimized trajectories avoid
such regions, confirming the method’s effectiveness.
Notably, 𝜁 = 0.3 achieves a favorable balance
between trajectory deviation and manipulability.
The observed increase in manipulability with
larger 𝜁 suggests that the most favorable postures lie
away from the reference path. Minor differences in
final manipulability are attributed to jerk
minimization delays. Since 𝜁 = 0.5 shows the largest
arrival error, adjusting the constraint coefficient α in
real time is recommended.
4.2.2 Scenario B: Low Manipulability
Trajectory
Figure 6 shows the transport trajectories, while Figure
7 presents the corresponding manipulability. Similar
to Scenario A, trajectory deviation increases with
larger 𝜁 values, and manipulability generally
improves as 𝜁 increases. The reference trajectory
0.6
0.7
0.8
0.9
1
00.511.52
Time [s]
Scaled manipulability
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
354

exhibits manipulability values near zero, whereas the
proposed method effectively maintains higher
manipulability, even for 𝜁 = 0.1, enabling singularity
avoidance.
These results indicate that manipulability
decreases near singularities, and the proposed method
effectively avoids such configurations. By
formulating sloshing suppression as a manipulability
optimization problem, the method simultaneously
enhances both manipulability and vibration
suppression. Under Scenario B, the method
demonstrates effectiveness for singularity avoidance.
Finally, Figure 8 illustrates the motion generated
by the proposed method. The container tilt aligns with
the direction normal to the liquid surface, confirming
the effectiveness of the control. The average and
maximum computation times are summarized in
Table 1. By avoiding a complex objective, the
proposed method achieved computation times below
10 ms in all cases, sufficient for 100 Hz real-time
control. A wider flexible constraint slightly increased
computation time, reflecting the expansion of the
feasible search space.
Table 1: Computation time under different constraints.
Condition
𝜁
0.0
0.1 0.3 0.5
Avg. time [ms] 0.182 0.472 0.807 1.08
Max. time [ms] 0.612 1.02 1.69 3.06
5 CONCLUSIONS
This study proposed a manipulability optimization
method that accounts for task-specific constraints,
such as end-effector speed and orientation during
liquid transfer. Trajectories were generated using a
minimum jerk model to achieve both vibration
suppression and high manipulability. By
incorporating trajectory flexibility as a constraint and
gradually tightening it, the method ensured timely
and feasible motion execution.
Experimental results confirmed that high-
manipulability trajectories can be achieved without
extending execution time, demonstrating the
method’s feasibility under time constraints. Although
the end time was fixed, further improvements could
be made by adapting it to the manipulator’s condition.
Future work will extend the constraint formulation to
both state and joint spaces and explore redundancy
resolution in highly constrained tasks.
REFERENCES
Diavareshkian, M. H., & Khalili, M. (2006). Simulation of
sloshing with the volume of fluid method. Fluid
Dynamics & Materials Processing, 2(4), 299–308.
Dufour, K., & Suleiman, W. (2020). On maximizing
manipulability index while solving a kinematics task.
Journal of Intelligent Robotic Systems, 100(1), 3–13.
Figure 8: Liquid transfer using tilting motion control. The red lines show the glass’s central axis and liquid surface’s
orientation. The different lengths of the vertical axis represent the tilt in the depth direction (t = 0.5 s, 1.5 s).
Figure 6: Liquid transferring trajectory (Scenario B).
Figure 7: Scaled manipulability (Scenario B).
0
0.2
0.4
0.6
0.8
1
0 0.5 1 1.5 2
Time [s]
Scaled manipulability
Manipulability Maximization of a Liquid-Handling Manipulator for Sloshing Suppression via Container Tilting
355
Flash, T., & Hogan, N. (1985). The coordination of arm
movements: An experimentally confirmed
mathematical model. The Journal of Neuroscience,
5(7), 1688–1703.
Haowen, Y., Laha, R., Figueredo, L., & Haddadin, S.
(2024). Enhanced Dexterity Maps (EDM): A new map
for manipulator capability analysis. IEEE Robotics and
Automation Letters, 9(2), 1628-1635.
Jin, L., Li, S., La, H. M., & Luo, X. (2017). Manipulability
optimization of redundant manipulators using dynamic
neural networks. IEEE Transactions on Industrial
Electronics, 64(6), 4710–4720.
Kavraki, L. E., Svestka, P., Latombe, J. C., & Overmars, M.
H. (1996). Probabilistic Roadmaps for Path Planning in
High-Dimensional Configuration Spaces, IEEE Trans.
on Robotics and Automation, 12(4), 556-580.
Kennel-Maushart, F., Poranne, R., & Coros, S. (2021).
Manipulability optimization for multi-arm
teleoperation. In Proceedings of the 2021 IEEE
International Conf. on Robotics and Automation
(ICRA) (pp. 3956–3962). IEEE.
LaValle, S. M., Kuffner, J. J. (2001). Rapidly-exploring
random trees: Progress and prospects, Algorithmic and
Computational Robotics, 303-307.
Maric, F., Limoyo, O., Petrovic, L., Ablett, T., Petrovic, I.,
& Kelly, J. (2019). Fast manipulability maximization
using continuous-time trajectory optimization. In
Proceedings of the 2019 IEEE/RSJ International
Conference on Intelligent Robots and Systems (IROS)
(pp. 8258–8264). IEEE.
Moriello, L., Biagiotti, L., Melchiorri, C., & Paoli, A.
(2018). Manipulating liquids with robots: A sloshing-
free solution. Control Engineering Practice, 78, 129–
141.
Muchacho, R. I. C., Laha, R., Figueredo, L. F. C., &
Haddadin, S. (2022). A solution to slosh-free robot
trajectory optimization. In Proceedings of the 2022
IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS) (pp. 223–230). IEEE.
Muller, M., Charypar, D., & Gross, M. (2003). Particle-
based fluid simulation for interactive applications. In
Proceedings of the 2003 ACM SIGGRAPH
/Eurographics Symposium on Computer Animation (pp.
154–159). ACM.
Wang, X., Li, X., Guan, Y., Song, J., & Wang, R. (2019).
Bidirectional potential guided RRT* for motion
planning. IEEE Access, 7, 95046–95057.
Yano, K., Higashikawa, S., & Terashima, K. (2001). Liquid
container transfer control on 3D transfer path by hybrid
shaped approach. In Proceedings of the 2001 IEEE
International Conference on Control Applications (pp.
1168–1173). IEEE.
Yano, K., & Terashima, K. (2001). Robust liquid container
transfer control for complete sloshing suppression.
IEEE Transactions on Control Systems Technology,
9(3), 483–493.
Yoshikawa, T. (1985). Manipulability of robotic
mechanisms. The International Journal of Robotics
Research, 4(2), 3–9.
Zhang, H., Sheng, Q., Hu, J., Sheng, X., Xiong, Z., & Zhu,
X. (2022). Cooperative transportation with mobile
manipulator: A capability map-based framework for
physical human-robot collaboration. IEEE/ASME
Transactions on Mechatronics, 27(6), 4396–4405.
APPENDIX
Only the main symbols frequently used throughout
the paper are listed here. Other symbols are defined
locally in the text.
Table A1: List of symbols.
Symbol Definition
𝑞
Joint angle vector
𝑞
Joint velocity vector
𝑥
End-effector pose
(position and orientation)
𝑥 =
𝑣
𝜔
End-effector velocity
(linear
𝑣, angular 𝜔)
𝐽
(
𝑞
)
Jacobian matrix of the
mani
p
ulato
r
𝑚(𝑞)
Manipulability index
𝜁
Deviation parameter for
flexible constraint
𝑎
(
𝑡
)
Time-varying scaling
coefficient
𝜃
Container tilt angle [rad]
𝑡,𝑡
Time, final time
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
356
