Pressing Force Regulation in Robotic 3D Printing

via CFD-Aided Nozzle Posture Control

Shinichi Ishikawa

, Ryo Yamada

, Wakana Tsuru

and Ryosuke Tasaki

Department of Mechanical Engineering, Aoyama Gakuin University, Kanagawa, Japan

Institute of Ocean Energy, Saga University, Saga, Japan

Keywords: Robotic 3D Printing, CFD Analysis, Force-Feedback Control, Extrusion Control, Force Sensing.

Abstract: In the 3D printing process of applying materials, inadequate extrusion pressure critically deteriorates the

deposition quality in robotic 3D printing. Feedback-based motion control with sensing and AI technology has

been studied to respond to uneven and flexible surfaces, but challenges remain in optimizing the application

force according to the situation. In this study, we investigate numerically and experimentally how the nozzle

can change its orientation during the printing motion in a way that reduces the extrusion force. Numerical

calculations are performed to derive the relationship between the clearance between the nozzle and the base

and the extrusion force for multiple nozzle orientation patterns. Based on the numerical results, the

relationship between the operating quantity (clearance) and the control quantity (maximum pressure and line

width) is expressed mathematically to predict the quality model based on numerical fluid dynamics. In a

variable-thickness printing experiment using a robot arm, a convex shape was reproduced by robot motion

control that continuously changed the nozzle orientation. The experimental results demonstrated that adjusting

the nozzle orientation effectively maintained extrusion force, preventing a reduction of approximately 0.01 N,

as verified through force sensor-based inspection.

1 INTRODUCTION

3D printing technology is a processing method that

creates 3D shapes by applying layers of material

ejected from a nozzle (Volodymyr K. et al., 2024).

Compared to conventional processing methods, this

method allows for more flexible processing, making

it suitable not only for desktop-scale printing but also

for large-scale printing such as architectural 3D

printing using concrete materials. Furthermore, as an

advanced application of 3D printing technology, the

technology is being developed for printing on the

ground (Salvatore B. et al., 2024), curved surfaces

(Jin Y. et al., 2016), and flexible surfaces (M.

Miyatake et al., 2020). However, the effects of

printing motion parameters and nozzle orientation on

the shape of the printing line and the underlying

foundation have not been fully elucidated.

Conventional additive technologies are mainly

used for printing on a flat surface and in environments

with little disturbance, and there are few examples of

https://orcid.org/0000-0002-8590-3019

https://orcid.org/0000-0002-3619-4498

printing on products or in environments with complex

conditions. Feedback-based 3D printing methods

using sensing methods (thickness control of printing

lines (Rob J. et al., 2017), width control of printing

lines (E. Shojaei et al., 2020), path change (S.

Ishikawa et al., 2023), and feed rate change (Philip F.

et al., 2022)) are being actively promoted to deal with

printing methods in complex environments with a lot

of uncertainty.

Figure 1: 3D printing process with CFD analysis and

motion control.

Ishikawa, S., Yamada, R., Tsuru, W. and Tasaki, R.

Pressing Force Regulation in Robotic 3D Printing via CFD-Aided Nozzle Posture Control.

DOI: 10.5220/0013748100003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 91-95

ISBN: 978-989-758-770-2; ISSN: 2184-2809

This study aims to clarify the effects of clearance and

nozzle orientation on the extrusion force using

numerical simulation and experiments. By

conducting numerical simulation under multiple

patterns of orientation angle conditions, the

relationship between the amount of manipulation,

including orientation and control in 3D printing is

evaluated to achieve quality model prediction based

on numerical fluid dynamics. The proposed 3D

printing approach with CFD analysis and motion

control is illustrated in Figure 1. In addition, a convex

shape is produced by a printing experiment utilizing

the orientation change of the nozzle by robot motion

control, and the effect of the orientation change of the

nozzle on the extrusion force is observed.

2 PRESSING FORCE CONTROL

AND ROBOTIC-ARM-BASED

3D PRINTING SYSTEM

2.1 Robotic-Arm-Based 3D Printing

and Force Measurement System

The Robotic-arm-based 3D printing system and the

measurement device for extrusion force measurement

are shown in Figure 2. The extruder using a stepping

motor is installed at the end of a 6-DOF robot arm to

perform multi-axis dispensing motions. A force

sensor with a fixed acrylic plate is used to measure

the force with which the dispensed material is

applied.

Figure 2: Appearance of the dispensing mechanism with

force measurement device.

A 6-axis force sensor with a rated capacity of ±50 N

in the Z-direction and a resolution of 1/4000 was

employed. Sensor values are measured in a PC with a

low-pass filter to remove noise.

Mortar putty (HI Level Super, KLASS) is used as

a printing material, which possesses specific viscosity

and yield value, making it suitable for construction

applications. The powdered putty is combined with

water, loaded into a syringe, and then dispensed.

Upon contact with water, the material undergoes a

reaction and solidifies after a certain period.

Figure 3: Simplified flow rate model for determining

dispensing operations.

2.2 Simplified Flow Rate Model for

Determining Dispensing Operations

A simplified flow rate model was developed to

determine the dispensing operation based on nozzle

movement, including nozzle orientation. The

relationship between the shape of the dispensed line

formed by dispensing, and printing parameters such

as clearance and nozzle orientation angle, is

represented as shown in Figure 3. Since the discharge

flow rate from the nozzle is equal to the dispensed

flow rate, this relationship can be expressed by the

continuity equation as shown in Equation (1).

In the simplified flow rate model represented by

Equation (1), the discharge flow velocity of the

material is denoted as 𝑈 [mm/s], the nozzle diameter

as 𝐷 [mm], and the nozzle feed velocity as v

[mm/s].

The dispensed line width, thickness, and cross-

sectional area correction coefficient are denoted as 𝑤

[mm], ℎ [mm], and 𝐶 [-], respectively. Based on our

previous research(S. Ishikawa et al., 2025), the value

of 𝐶 is assumed to be 0.8.

In the proposed convex shape printing method,

convex shapes are formed by altering the thickness

through changes in nozzle orientation. To establish a

one-to-one relationship between the rotation direction

and clearance variation, the rotation center during

nozzle orientation changes is set at the edge of the

nozzle outlet, as illustrated in Figure 3.

𝜋𝐷



𝑈/4  ℎ𝑤𝐶𝑣



)

ℎℎ



𝐷sin𝜃

)

The line thickness ℎ of the printed structure is

determined by the sum of the clearance ℎ

𝐺

at the

lowest point of the nozzle outlet and the clearance

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

variation due to the orientation angle 𝜃. The

dispensing operation is determined using this

relationship. The correlation between clearance and

line thickness is expressed in Equation (2).

3 NUMERICAL SIMULATION OF

DISPERSED MATERIAL

Using numerical simulation software, the effect of the

proposed convex-shape printing operation on mortar

putty was analysed. Pressure distribution changes

during clearance increases and nozzle orientation

changes are visualized.

3.1 Numerical Calculation Method

Numerical calculations were conducted to visualize

pressure distribution. As shown in Figure 3, the

mortar putty is discharged from the nozzle outlet and

flows outside the calculation domain. The calculation

focused on a steady-state flow within the domain. The

calculation domain is indicated in Figure 4. The

steady, incompressible Navier-Stokes equations

for mortar putty-air two-phase flow were solved

using Ansys Fluent 2024 R2. The calculation

conditions are summarized in Table 1.

Figure 4: Calculation domain for simulate of 3D printing

process.

Table 1: Main parameters of 3D printing simulation.

Nozzle diameter D [mm] 10

Feed velocit

[mm/s] 10

Dis

ensin

velocit

U [mm/s] 5.3

Clearance h

[mm] 4

Nozzle orientation angle θ [°]

Density ρ [kg/m

] 800

Viscosity µ [kg/(m・s)]

1000

Gravitational acceleration

[m/s

] 9.81

The viscosity of the mortar putty was estimated

based on literature values (N. Izumo et al., 2008), and

its density was measured from the bulk density. Since

the flow of mortar putty is dominated by viscous

forces over inertial forces, it was treated as laminar.

For this flow analysis, the Volume of Fluid (VoF)

model, a type of two-phase flow calculation model,

was utilized. Assuming symmetry in the 𝑧-𝑥 plane,

only half of the domain was solved. A structured grid

with 250,000 nodes was employed.

The 𝑧-𝑥 plane was set as a symmetry boundary,

and the average velocity of mortar putty at the nozzle

outlet tip, as shown in Table 1, was applied at the inlet

boundary in Figure 4. The lower wall velocity was set

to -𝑣

𝑥

, solving the flow in the relative coordinate

system of the nozzle. For the air flow outside the

nozzle, the right boundary of Figure 3 was set as an

inlet boundary for air with a velocity of -𝑣

𝑥

The nozzle and lower wall were treated as no-slip

walls, while other surfaces, including the mortar-air

boundary, were treated as open to the atmosphere.

The computational domain reflecting these

conditions is illustrated in Figure 4.

3.2 Pressure Distribution Changes

by Nozzle Orientation

The effects of conventional 3-degree-of-freedom

printing and the proposed multi-degree-of-freedom

printing methods on discharged materials were

investigated through numerical simulation. Based on

the simplified flow rate model in Equation (1), a

scenario was considered where the printed line

(a) without clearance change and orientation change

(b) with clearance change to 8 mm

Figure 5: Pressure distribution in longitudinal section and

on substrate.

Pressing Force Regulation in Robotic 3D Printing via CFD-Aided Nozzle Posture Control

thickness varies from 4 mm to form a convex shape.

Two cases were compared: increasing the clearance

from 4 mm to 8 mm to achieve a 4 mm thickness

increase and altering the nozzle orientation to achieve

the same thickness increase.

For the conditions in Table 1, Figure 5(a) shows

the pressure results obtained by the simulation for the

vertical and bottom surfaces of half the domain.

Figures 5(b) and (c) depict the results for an 8 mm

clearance increase and a 23.6° nozzle orientation

change, respectively. Comparing Figures 5(b) and (c),

the positive pressure distribution range of the mortar

putty in contact with the bottom surface was broader

in the clearance increase case. However, the

maximum pressure was 8,245 Pa in the nozzle

orientation case and 5,794 Pa in the clearance

increase case, showing a 1.42-fold higher pressure in

the former.

4 MEASUREMENT OF

PRESSING FORCE IN CONVEX

SHAPE PRINTING

In convex printing using nozzle orientation changes,

multiple convex shapes were reproduced to

investigate the effect of nozzle orientation changes on

extrusion force. The extrusion force was extracted

from the load values.

4.1 Experimental Conditions

Using the experimental setup shown in Figure 2, the

extrusion force during the printing of identical convex

shapes was measured and compared for cases of

clearance change alone and nozzle orientation change

alone. Both the clearance and orientation change

cycles were 4 seconds, with convex shapes formed at

four locations. Other printing parameters were

determined by referencing section 3 to match

numerical calculation conditions.

4.2 Results of The Convex Shape

Printing Experiment

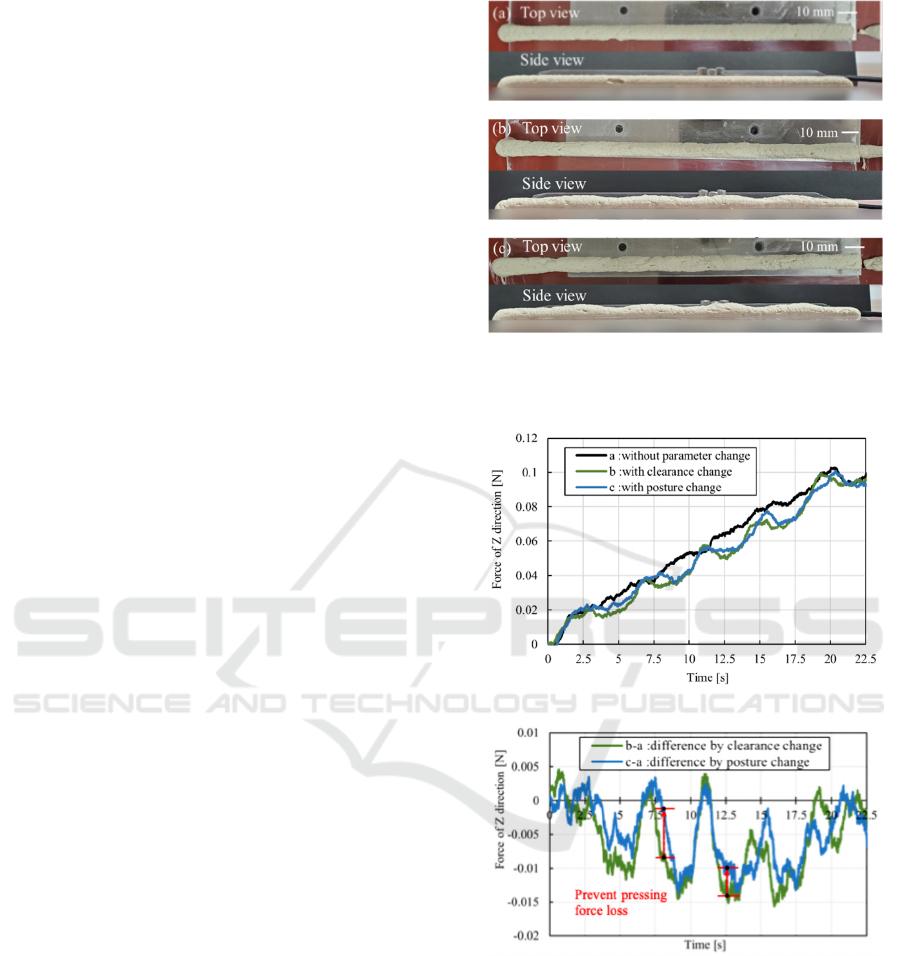
The printed line appearances for each operation are

shown in Figure 6, and the Z-direction load

measurements from the force sensor are presented in

Figure 7. Figure 7(a) confirms that extrusion force

decreases during convex shape printing. Figure 7(b)

extracts extrusion force changes by subtracting sensor

values during printing without clearance or

orientation changes. It shows that the reduction in

(a) without clearance change and orientation change

(b) with clearance change

Figure 6: Printed line by printing motion with clearance and

orientation change.

(a) measured pressing force of z direction

(b) difference in each force of z direction

Figure 7: Comparison of measured pressing forces by each

printing motion.

extrusion force during convex shape printing is

approximately 0.01 N smaller in the nozzle

orientation case than in the clearance change case.

This suggests that limiting clearance increases

through orientation changes can mitigate extrusion

force reduction.

Furthermore, this experimental tendency is

consistent with the CFD analysis presented in Section

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

3. The numerical results indicated that, for the same

convex height increase, the nozzle orientation change

produced a more concentrated pressure distribution

and a higher maximum pressure (1.42 times greater)

compared to the clearance increase case. The

experimental observation of smaller force reduction

therefore supports the simulation outcome,

confirming that nozzle orientation control effectively

maintains extrusion pressure. This agreement

between simulation and experiment demonstrates that

the CFD-derived pressure distribution can serve as a

predictive model for extrusion force behavior in

robotic 3D printing.

5 CONCLUSIONS

In this study, a 3D printing method utilizing nozzle

orientation changes via a robotic arm was verified

through numerical simulation and physical

experiments to suppress the decrease in extrusion

force and achieve high-quality 3D-printed structures.

In the numerical simulation, the effect of the

clearance between the nozzle and the base on the

extrusion force was evaluated, considering multiple

nozzle orientation angles. Furthermore, it was

confirmed that the maximum pressure becomes 1.42

times greater during orientation changes compared to

clearance changes, indicating its contribution to the

local enhancement of the extrusion force.

Furthermore, in experiments using robotic motion

control, the printing of convex shapes was

successfully reproduced through continuous nozzle

orientation changes. Quality inspection utilizing a

force sensor confirmed that the proposed printing

method suppressed the reduction in extrusion force by

approximately 0.01 N.

In this paper, a new 3D printing framework based

on CFD analysis is introduced, and this study

provides novel insights into the effect of nozzle

orientation on extrusion force during robotic 3D

printing. These findings highlight a novel design

perspective in robotic 3D printing that leverages

multi-axis motion planning informed by fluid

dynamics.

REFERENCES

Jin Yuan, Jianke Du, Yong He, and Guoqiang Fu (2016).

Modeling and process planning for curved layer fused

deposition, The International Journal of Advanced

Manufacturing Technology, Volume 91, pp. 273–285.

Mako Miyatake and Aoi Watanabe (2020). Interactive cake

decoration with whipped cream, ICMR '20:

International Conf. on Multimedia Retrieval, pp. 7–11.

Naoto Izumo and Hisanori Oda (2008). Observing the cure

processes of cement materials based on static viscosity

measurements, Ceramics Japan, Volume 3.

Philip F. Yuan, Qiang Zhan, Hao Wu, Hooi Shan Beh, and

Liming Zhang (2022). Real-time toolpath planning and

extrusion control (RTPEC) method for variable-width

3D concrete printing, Journal of Building Engineering,

Volume 46, 103716.

Rob J. M. Wolfs, Freek P. Bos, Emiel C. F. van Strien, and

Theo A. M. Salet (2017). A real-time height

measurement and feedback system for 3D concrete

printing, High Tech Concrete: Where Technology and

Engineering Meet, pp. 2474–2483.

Salvatore Bruno, Giuseppe Cantisani, Antonio D’Andrea,

Kristian Knudsen, Giuseppe Loprencipe, Laura

Moretti, et al. (2024). A small robot to repair asphalt

road potholes, Infrastructure, Volume 9, pp. 210–227.

Shinichi Ishikawa, Takahito Yamashita, and Ryosuke

Tasaki (2023). Vision-based monitoring and control for

3D printing process with dynamic ROI and path

modification algorithm, Journal of Advances in

Information Technology, Volume 14, No. 6, pp. 1443–

1449.

Shinichi Ishikawa, Ryo Yamada, and Ryosuke Tasaki

(2025). High-sensitivity Interlayer Force Measurement

and Multi-layer Smoothing Control for 3D Printing on

Uneven Surfaces, SICE Journal of Control,

Measurement, and System Integration, Volume 18,

Issue 1.

Shojaei Barjuei, E., Courteille, E., D. Rangeard, F. Marie,

and A. Perrot (2020). Real-time vision-based control of

industrial manipulators for layer-width setting in

concrete 3D printing applications, Advances in

Industrial and Manufacturing Engineering, Volume 5,

100094.

Volodymyr Khyzhynskyi, Mykola Lampeka and Valerii

Strilets (2024). The history of the development of 3D

printing technologies and their use in world artistic

ceramics, History of science and technology, Volume

14, issue 1, pp. 152-183.

Pressing Force Regulation in Robotic 3D Printing via CFD-Aided Nozzle Posture Control