3D Hand-Eye Calibration for Collaborative Robot Arm:

Look at Robot Base Once

Leihui Li

, Lixuepiao Wan

, Volker Krueger

and Xuping Zhang

1,∗

Department of Mechanical and Production Engineerin, Aarhus University, Denmark

Department of Computer Science, Lund University, Lund, Sweden

Keywords:

Hand-Eye Calibration, 3D Vision, Collaborative Robot, Robot Arm.

Abstract:

Hand-eye calibration is a common problem in the ﬁeld of collaborative robotics, involving the determination of

the transformation matrix between the visual sensor and the robot ﬂange to enable vision-based robotic tasks.

However, this process typically requires multiple movements of the robot arm and an external calibration

object, making it both time-consuming and inconvenient, especially in scenarios where frequent recalibration

is necessary. In this work, we extend our previous method which eliminates the need for external calibration

objects such as a chessboard. We propose a generic dataset generation approach for point cloud registration,

focusing on aligning the robot base point cloud with the scanned data. Furthermore, a more detailed simulation

study is conducted involving several different collaborative robot arms, followed by real-world experiments in

an industrial setting. Our improved method is simulated and evaluated using a total of 14 robotic arms from 9

different brands, including KUKA, Universal Robots, UFACTORY, and Franka Emika, all of which are widely

used in the ﬁeld of collaborative robotics. Physical experiments demonstrate that our extended approach

achieves performance comparable to existing commercial hand-eye calibration solutions, while completing

the entire calibration procedure in just a few seconds.

1 INTRODUCTION

3D vision systems, particularly those utilizing point

cloud data, provide detailed geometric surface in-

formation that enables comprehensive spatial under-

standing (Munaro et al., 2016). This capability has

signiﬁcantly advanced modern manufacturing sys-

tems (Wang et al., 2021, 2017), especially in the

ﬁelds of collaborative robot and automated opera-

tions (Robinson et al., 2023; Halme et al., 2018).

Furthermore, the integration of perception sensors

with robotic manipulators has greatly enhanced au-

tomation applications that require vision-based intel-

ligent control and manipulation (Zhou et al., 2021b;

Ten Pas et al., 2017; Zhou et al., 2021a). A fun-

damental problem in collaborative robot is establish-

ing accurate coordination between the sensing system

(eye) and the tool center point (hand) (Horaud and

Dornaika, 1995; Jiang et al., 2022; Enebuse et al.,

2021). This coordination, known as hand-eye cali-

bration, determines the spatial transformation, which

consists of both translation and rotation. Widely

∗

Corresponding author

used methodologies (Enebuse et al., 2021, 2022; Wi-

jesoma et al., 1993) typically depend on specialized

calibration equipment and complex procedures, creat-

ing practical limitations in dynamic industrial settings

where systems require frequent recalibration. In this

paper, we aim to achieve fast and effective hand-eye

calibration through 3D vision.

Calibration targets in conventional hand-eye cal-

ibration are essential components (Tsai et al., 1989;

Strobl and Hirzinger, 2006), with checkerboards and

circles being the most common standard patterns

(Mallon and Whelan, 2007). By executing multi-

ple collaborative robot arm movements while acquir-

ing corresponding images, the homogeneous trans-

form equation is constructed and solved to estimate

the hand-eye transformation (Wang and Song, 2024).

Such conventional target-based approaches have in-

herent limitations: mandatory manual integration of

calibration targets, inevitably approximate solutions

due to their nonconvex nature (Wu et al., 2020), and

multiple robot movements for data collection that sig-

niﬁcantly increase time consumption (Zhou et al.,

2023; Allegro et al., 2024; Ma et al., 2018).

To address challenges in traditional hand-eye cal-

Li, L., Wan, L., Krueger, V. and Zhang, X.

3D Hand-Eye Calibration for Collaborative Robot Arm: Look at Robot Base Once.

DOI: 10.5220/0013738500003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 333-341

ISBN: 978-989-758-770-2; ISSN: 2184-2809

333

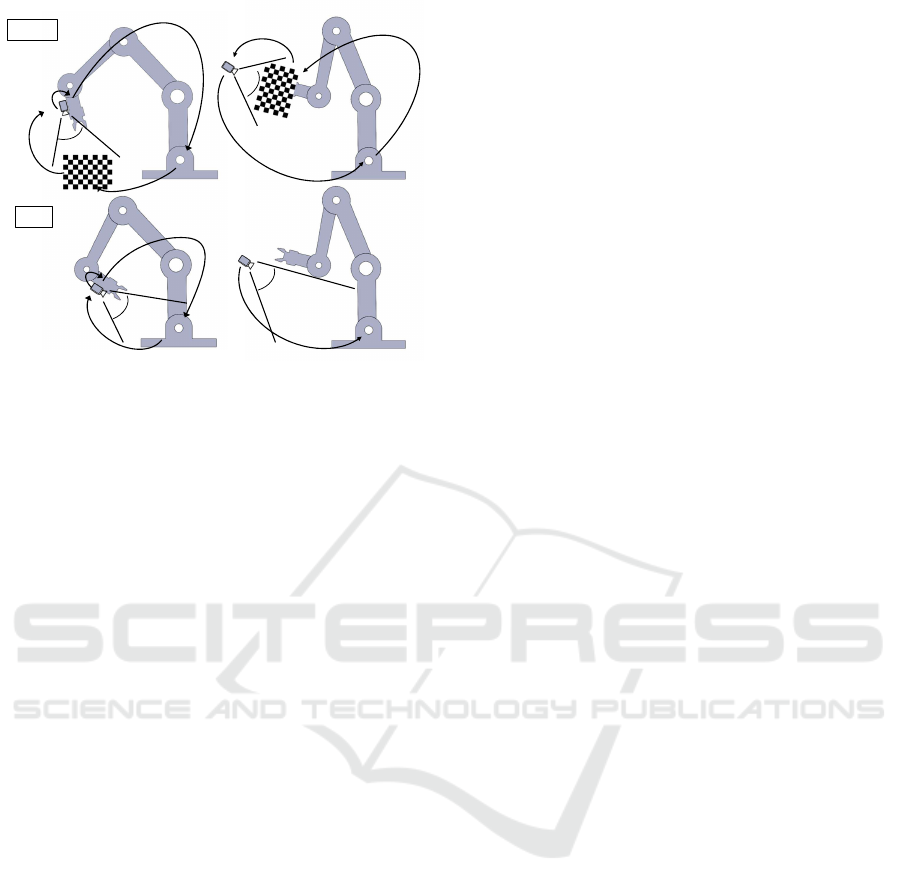
FoV

𝑇





𝑇





𝑇





? 𝑇





𝑇





𝑇





𝑇





𝑇





𝑇





𝑇





𝑇





Eye-to-hand calibrationEye-in-hand calibration

Ours

Classic

Figure 1: Our proposed hand-eye and the traditional cali-

bration that needs the external calibration objects.

ibration, we build on our previous work (Li et al.,

2024), which retains user-friendliness by eliminat-

ing additional calibration targets and using the robot

base as a uniﬁed target, enabling rapid calibration.

In this paper, a generic dataset generation method is

proposed to make our approach applicable to a wide

range of collaborative robots. Additionally, 14 robotic

arms are used in the simulation to thoroughly evaluate

the robustness and accuracy of our method, demon-

strating its feasibility. Finally, a physical experiment

compares our method with a commercial hand-eye

calibration solution, demonstrating its practical appli-

cability.

Our main contributions are as follows:

1. We improve and develop a generic dataset genera-

tion method: in addition to capturing point clouds

around the robot base on hemispheres with vary-

ing radii, we also simulate realistic robot poses by

exploring diverse joint angle combinations.

2. A total of 14 collaborative robot arms from 9

brands are included in our study, each contribut-

ing 900 hand-eye calibration results. Individual

and aggregated results are analyzed, demonstrat-

ing the approach’s generalizability.

3. Real-world experiments are conducted in an in-

dustrial setting, where our proposed method is

compared with a commercial calibration setup.

Our method is validated using both single and

multiple joint conﬁgurations, demonstrating its

effectiveness and comparable performance.

2 RELATED WORK

Hand-eye calibration is a prerequisite for vision-

guided robotic manipulation systems using collabo-

rative robot arms (Hong and Ha, 2025), and the ac-

curacy of this calibration fundamentally determines

the subsequent precision of vision-based control and

manipulation within the system. To compute the un-

known transformation between a robot end-effector

and a camera, the methodological approaches to ad-

dressing hand-eye calibration can be categorized into

(Enebuse et al., 2021): solving homogeneous trans-

form equations, reprojection error minimization tech-

niques, and learning-based methods.

The conventional equation formulations can be

represented as (Zhu et al., 2024):AX = X B (Shiu and

Ahmad, 1987) or AX = Y B (Zhuang et al., 1994).

The former approach determines the hand-eye ma-

trix X through multiple sets of robot movements.

To eliminate error propagation inherent in this for-

mulation and improve noise sensitivity, Zhuang and

Shiu (Zuang and Shiu, 1993) proposed a sequential

method for solving matrix X . Recently, Ma et al.

(Ma et al., 2016) proposed novel probabilistic ap-

proaches that extend the Batch method to ﬁlter out-

lier data. The second equation seeks to simultane-

ously determine both the hand-eye matrix X and the

transformation matrix Y from the robot base to the

world coordinate. To solve this equation, many solu-

tion strategies utilize linear least-squares minimiza-

tion combined with iterative optimization schemes

(Tabb and Ahmad Yousef, 2017). In response to these

approaches, Ha (Ha, 2022) proposed a probabilistic

framework that elucidates the ambiguous aspects of

existing methods by revealing their underlying as-

sumptions about system noise. An alternative ap-

proach leverages reprojection error minimization for

hand-eye calibration. Based on this principle, Kenji

and Emanuele (Koide and Menegatti, 2019) proposed

a hand–eye calibration method that minimizes repro-

jection error via pose graph optimization, allowing ro-

bust estimation across various camera models. How-

ever, these conventional methods and their deriva-

tive approaches typically require either multiple robot

movements (at least two), additional calibration tar-

gets, or suffer from high algorithmic complexity and

extended computational time.

To overcome the limitations of conventional ap-

proaches, learning-based methodologies have been

progressively incorporated into hand-eye calibration

procedures. Hua and Zeng (Hua and Zeng, 2021)

established coordinate transformation relationships

through neural network training, achieving enhanced

grasping accuracy even under the inﬂuence of noise

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

334

perturbations. In constrained surgical scenarios, Krit-

tin et al. (Pachtrachai et al., 2021) estimated hand-eye

transformation through a deep convolutional network,

leveraging temporal information between frames and

kinematic data without requiring calibration objects.

Bahadir et al. (Bahadir et al., 2024) proposed Con-

tinual Learning-based approaches that enable pro-

gressive extension of the calibration space without

complete retraining, while accommodating changes

in camera pose over time. Nevertheless, exist-

ing learning-based methods still present considerable

room for improvement. The associated neural net-

works exhibit high computational complexity, lim-

ited generalizability for straightforward implementa-

tion in common robotic manipulators, and in some

cases, continued dependence on external calibration

objects. Furthermore, some approaches are limited to

either eye-in-hand or eye-to-hand calibration, failing

to address both scenarios.

In comparison with the aforementioned method-

ologies, our proposed method maintains the advan-

tage of calibration-object-free operation while accom-

modating both eye-in-hand and eye-to-hand calibra-

tion conﬁgurations. By looking at the robot base, a

closed kinematic chain is established, allowing the

transformation matrix between the camera and the

robot ﬂange to be determined straightforwardly. In

addition, we introduce a dataset generation method

for point cloud registration of the robot base, en-

hancing the generality of our approach. Simula-

tions involving 14 commonly used collaborative robot

arms, along with physical experiments comparing our

method to commercial solutions, demonstrate the ap-

plicability and effectiveness of the proposed method.

3 PROBLEM DEFINITION AND

METHODS

In vision-guided collaborative robot systems, hand-

eye calibration aims to determine the transformation

between the camera and the tool center point (eye-in-

hand) or the robot base (eye-to-hand). In eye-in-hand

calibration, the camera is mounted on the robot’s end-

effector, moving with the arm. In contrast, in eye-to-

hand calibration, the camera is ﬁxed in the environ-

ment to observe the robot’s workspace. To formalize

this, we deﬁne the coordinate systems: the robot base

as F

, the tool center point as F

, calibration object as

, and the camera as F

3.1 Eye-in-Hand Calibration

In the eye-in-hand conﬁguration, the camera is rigidly

mounted on the robot’s ﬂange, as illustrated in the

ﬁrst one in Figure 1. The primary objective is to

compute the rigid transformation matrix between the

camera coordinate system and the tool center point

(TCP) frame. This problem is commonly formulated

as AX = XB, where X represents the transformation to

be solved. This calibration typically requires the robot

to move to multiple poses while observing a calibra-

tion target. Speciﬁcally, it can be expressed as

−1

T =

−1

(1)

where i and j denote two distinct robot poses from the

set of calibration measurements, and

T represents the

transformation matrix from the frame of the tool cen-

ter point to the robot base coordinate system.

T can

be computed through forward kinematics,

T is the

unknown hand-eye transformation matrix to be deter-

mined, and

T denotes the transformation from the

calibration object frame to the camera frame.

3.2 Eye-to-Hand Calibration

In the eye-to-hand conﬁguration, the camera is

mounted at a ﬁxed position within the workspace, ex-

ternal to the robot arm. This setup allows the camera

to maintain a static, global viewpoint while the robot

manipulator performs its movements. The primary

objective of eye-to-hand calibration is to determine

the rigid transformation matrix between the camera

coordinate system and the robot base coordinate sys-

tem. Through multiple movements of the calibration

board at the robot arm’s end-effector, the mathemati-

cal relationship can be established:

−1

T =

−1

(2)

where

T is the unknown transformation from the

camera coordinate system to the robot base coordinate

system to be calculated, and

T denotes the transfor-

mation from the camera frame to the observed cali-

bration target, measured at different robot poses.

3.3 Look at Robot Base Once

The proposed methodology eliminates the need for a

dedicated calibration object by directly observing the

robot base, as illustrated in the second setup in Fig-

ure 1. Given the 3D data of the robot base, its 6D pose

can be estimated, allowing the determination of the

transformation matrix between the camera coordinate

3D Hand-Eye Calibration for Collaborative Robot Arm: Look at Robot Base Once

335

system and the robot base coordinate system. This ap-

proach can be further extended to compute the trans-

formation matrix between the TCP coordinate system

and the camera coordinate system.

Given the captured robot base point cloud P =

∈ R

|i = 1 . . . n} and the reference model point

cloud Q = {q

∈ R

| j = 1. . . m}, the objective of

registration is to ﬁnd the optimal rigid body trans-

formation parameters: an orthogonal rotation matrix

R ∈ SO(3) and translation vector t ∈ R

that minimize

the error between the transformed actual point cloud

and the reference model point cloud. The optimiza-

tion objective can be expressed as

min

R,t

∑

i=1

min

j=1

∥p

− (Rq

+t)∥

(3)

where ∥p

− (Rq

+t)∥

is the Euclidean distance be-

tween the acquired point cloud and the reference point

cloud of robot base. Due to a scale mismatch between

the reference model and the acquired data, a pre-

transformation of the reference data, denoted

re f

′

re f

T, is

applied. The registration module provides the trans-

formation

re f

′

T, leading to the formulation in Eq. 4.

re f

T =

re f

′

re f

′

re f

T (4)

T =

re f

−1

(5)

Here, the frame of the reference data is aligned with

the frame of the robot base in the real world, which

gives Eq. 5. For eye-in-hand calibration, each move-

ment forms a closed kinematic chain as

I =

T (6)

The transformation matrix

T therefore can be ob-

tained by performing the transformation as

T =

−1 c

−1

(7)

The eye-in-hand setup is more computationally

challenging due to the moving camera frame, whereas

in eye-to-hand calibration,

T can be estimated

straightforwardly using a point cloud registration

module. Therefore, we adopt the eye-in-hand con-

ﬁguration for experimental validation to demonstrate

the robustness of our approach.

The main challenge lies in generating a dataset

of robot base point clouds for registration training,

where both the source data (captured point clouds)

and the target data (reference model) are represented

as point clouds. We begin by capturing the robot

base through simulated 3D camera views positioned

around a sampled hemisphere centered at the base ori-

gin. Additionally, to enhance realism, we augment the

dataset by simulating valid robot poses based on joint

constraints, reﬂecting realistic conﬁgurations seen in

actual applications. Both datasets are used for train-

ing the point cloud registration network.

The ﬂowchart of our proposed method is illus-

trated in Figure 2, where the ﬁrst step involves mov-

ing the robot arm to position the robot base within

the camera’s ﬁeld of view. Given the

T, which can

be estimated by the point cloud registration module,

and

T, provided by forward kinematics, the

T can

ﬁnally be estimated as the result of the hand-eye cali-

bration.

𝑇





𝑇





Camera-to-Base

Movement

Base Point

Cloud

Acquisition

Point Cloud

Registration

Collaborative Robot

Configuration

Hand-Eye

Calibration

𝑇





Figure 2: Flowchart of the developed hand-eye calibration.

4 EXPERIMENTS

4.1 Preparation and Experiment Setup

The robot arms used in our simulation environment

are listed in Table 2. We utilize PyBullet as the sim-

ulation platform, where the robot arm is represented

in URDF and OBJ ﬁle formats for loading and gen-

erating the trainable dataset. PREDATOR (Huang

et al., 2021), a registration network designed for low-

overlap point clouds, is adopted in our study, fol-

lowed by an ICP reﬁnement step. This combination,

as shown in our previous work (Li et al., 2024), im-

proves robustness under partial overlap between the

captured data and the robot base reference model.

In our study, the raw point clouds are used with-

out background ﬁltering. The camera is positioned on

a virtual hemisphere with radii of 0.5 and 0.7 meters,

capturing data from multiple perspectives to simulate

real 3D camera acquisition. The ﬁnal dataset, avail-

able online, which is combined with realistic simu-

lated acquisition data, is used for training and is de-

tailed in Table 1. Five random transformation ma-

trices are applied to the captured data, and the point

clouds are downsampled with a 2 mm voxel size.

Table 1: The size of the dataset for registration training.

FR3 Gen3 iiwa 7 iiwa 14

CRX

-10iA

CRX

-5iA

UR10e

1224 1074 810 954 1230 1026 816

UR5e xArm6 xArm7

CRB

15000

HC10 EC66 EC63

1110 756 1140 768 1104 1014 1140

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

336

FR3 Gen3 iiwa7 iiwa14 CRX-5iA CRX-10iA UR10e

UR5e xArm7

xArm6

CRB15000 HC10 EC66 EC63

Figure 3: Visualization of randomly selected robot base-looking poses for various robotic manipulators, with one representa-

tive joint conﬁguration shown.

Table 2: The collaborative robot arm used in our study.

Index Robot Arm Manufacturer

1 FR3 Franka Robotics

2 Gen3 Kinova

3 iiwa 7 KUKA

4 iiwa 14 KUKA

5 CRX-5iA FANUC

6 CRX-10iA FANUC

7 UR10e Universal Robots

8 UR5e Universal Robots

9 xArm6 UFACTORY

10 xArm7 UFACTORY

11 CRB 15000 ABB

12 HC10 Yaskawa Motoman

13 EC66 Elite Robots

14 EC63 Elite Robots

4.2 Experimental Results

We evaluate the proposed approach in simulation,

where the ground-truth transformation between the

camera and TCP frame is known. For each robot

arm, 30 random poses are generated within realis-

tic joint angle limits to ensure kinematic feasibility,

where the camera looks at the robot base and the joint

rotations differ by at least 20 degrees to avoid near-

duplicate conﬁgurations, as shown in Figure. 3. In

all selected poses, the robot base remains within the

camera’s ﬁeld of view to satisfy the method’s require-

ments. At each pose, the end-effector-mounted 3D

camera captures multiple base scans, each yielding an

individual calibration result.

The ﬁnal calibration result is obtained by averag-

ing the rotation matrices in quaternion space and the

translation vectors in Euclidean space. Ideally, the

hand-eye calibration results obtained from the poses

match the ground truth (

R and

t), meaning the RTE

and RRE in translation and rotation should be zero,

RTE = ∥t −

t∥

(8)

RRE = arccos



trace(R

R) − 1



(9)

In addition to 30 unique base-looking poses for

each robotic arm, we captured 30 repeated scans per

pose, resulting in 900 calibration results per robot.

The calibration performance across all robot arms is

analyzed. As shown in Figure 4, it illustrates the av-

erage deviations in position and rotation errors, and

reports the median and standard deviation for each

robot. According to the results, the positional devi-

ation for all poses remains below approximately 1.5

mm, and most rotational deviations are under 0.5

◦

The largest deviation is observed in the Gen3 robot

arm. Overall, considering the point cloud voxel size

of 2 mm, the tested poses yield reliable calibration

performance, with a mean error of 1.29 mm in posi-

tion and 0.39

◦

in rotation.

Figure 4: The hand-eye calibration results calculated from

all poses for each robot arm are shown, with the mean value

represented by a black dot. In the box plot, the horizontal

line indicates the median value, while the top and bottom

edges represent the standard deviation.

At each pose, 30 sets of 3D data from the robot

base are collected, resulting in 30 calibration results.

The deviation of different poses is shown in Figure.

3D Hand-Eye Calibration for Collaborative Robot Arm: Look at Robot Base Once

337

5. According to the results, the positional deviation

for each pose ranges from 1 mm to 1.6 mm, with the

largest variation observed in robot CRX-5iA. The ro-

tational deviation ranges from 0.16

◦

to 1

◦

, with the

highest occurring in the Gen3 robot. The results in-

dicate that, for the tested robot arm with different

poses, the proposed method generally achieves a sim-

ilar level of accuracy; that is, our method does not rely

on any speciﬁc pose of the robot arm.

Figure 5: The differences between poses are illustrated by

data points connected with red and blue lines, representing

positional and rotational deviations, respectively.

This deviation, observed in the simulation envi-

ronment, primarily arises from registration errors and

the density of the point clouds, including both the re-

trieved data and the standard model. However, in real-

world applications, additional factors such as cam-

era imaging inaccuracies, point cloud noise, and dis-

crepancies between the CAD model and the scanned

robot base can further contribute to calibration errors.

Therefore, real-world experiments are conducted to

compare our proposed method with current commer-

cial and mature solutions.

4.3 Real-World Experiments

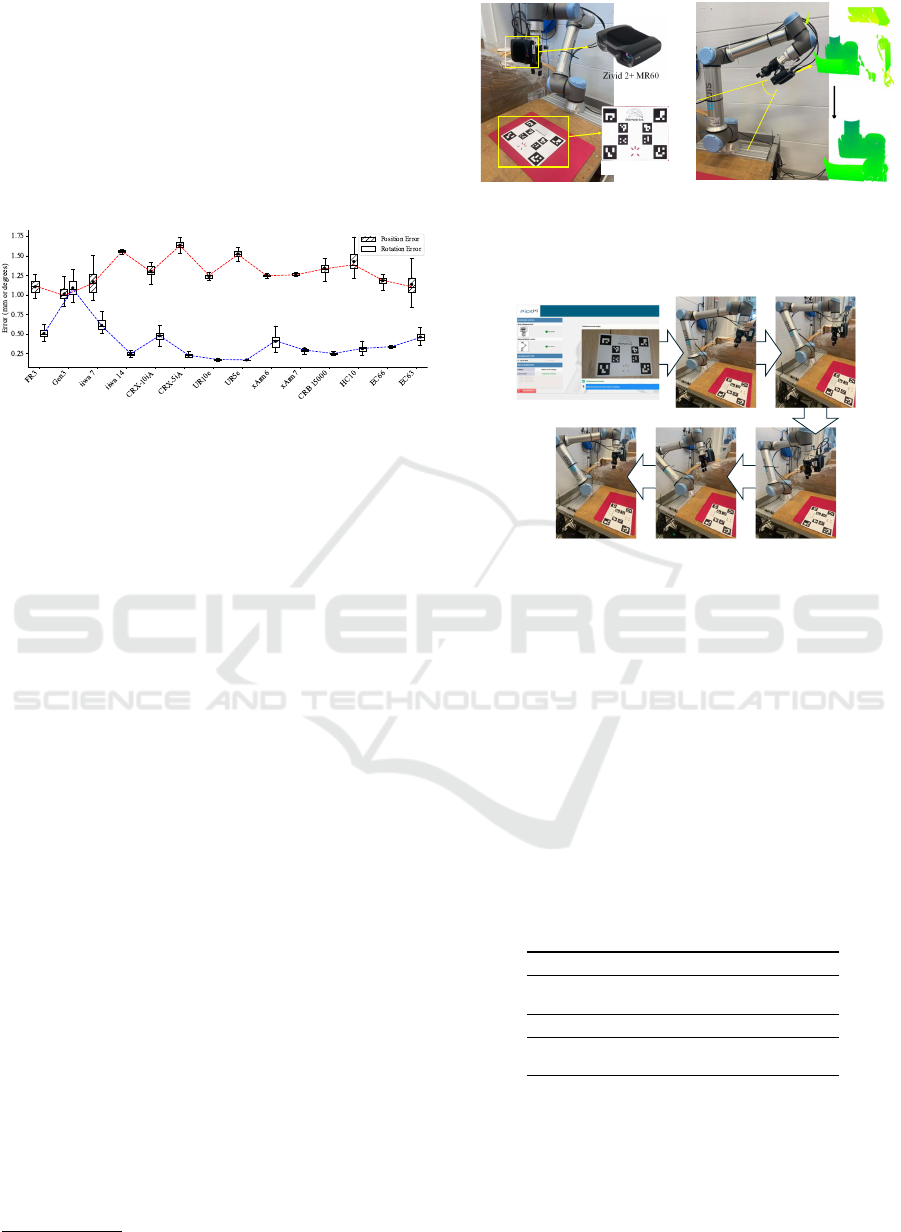
The experiment is conducted on the UR10e robot

with a high-accuracy 3D camera, the Zivid 2+ MR60,

which achieves a spatial resolution of 0.24 mm at

a working distance of 60 cm and generates highly

detailed point clouds with a density of 5,000 points

per cm². Although a high-precision 3D camera was

used for real-world validation, the method is sensor-

agnostic and applicable to other 3D cameras capable

of capturing the robot base geometry. The experimen-

tal setup is shown in Figure. 6a, where a calibration

board is needed. Figure. 6b illustrates the calibration

setup, with the camera oriented toward the robot base.

We compared our method with the current com-

mercial eye-in-hand calibration solution, BM-HEC

which is based on the AX = XB formulation. The tra-

ditional calibration process was repeated four times,

as shown in Figure 7, where multiple robot move-

ments are required during each calibration. Our

www.bitmetrics.es

Zivid 2+ MR60

Calibration Object

Eye-in-hand calibration setup

Cropped using

axis range

constraints

Field of view

(a)

Zivid 2+ MR60

Calibration Object

Eye-in-hand calibration setup

Cropped using

axis range

constraints

Field of view

(b)

Figure 6: (a) Traditional calibration with external object and

multiple robot movements. (b) Our calibration focusing on

the robot base without external object.

BM-HEC configuration GUI

Figure 7: Traditional calibration requires multiple move-

ments to capture the calibration object from different per-

spectives.

method was also performed four times, with each in-

dividual scan producing a complete calibration result.

The calibration process typically takes an average of

2 minutes and 48 seconds, requiring 14 poses and im-

ages of the calibration board placed on the table. In

contrast, our method completes the calibration in just

a few seconds with a single pose. The average cali-

bration results, i.e., the rigid relationship between the

robot ﬂange and the camera frame, are shown in Ta-

ble 3, where the rotation in Euler space and position

in Euclidean space are provided.

Table 3: Comparison of Eye-in-Hand Calibration with a

Commercial Calibration Solution.

Method TX (m) TY (m) TZ (m) Time

BM-HEC -0.054 -0.094 0.127 2m48s /

per calibOurs -0.051 -0.096 0.125

Method RX (rad) RY (rad) RZ (rad) Time

BM-HEC 0.013 0.044 0.017 6s /

per calibOurs 0.014 0.044 0.019

According to the results in Table 3, The offsets

between our method and BM-HEC are 3 mm, 2 mm,

and 3 mm in terms of position, and 0.001 and 0.002 in

rotation along the X and Z axes, respectively. The off-

set along the Y-axis is nearly zero. Most importantly,

the calibration time of our proposed method is within

6 seconds, whereas the traditional method takes over

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

338

Pose#1 Pose#2 Pose#3 Pose#4 Pose#5 Pose#6

Figure 9: Different poses used in our proposed hand-eye calibration method.

2.5 minutes, requiring multiple robot movements and

a physical external calibration object.

Furthermore, given a single pose with multiple

frames captured at that pose, calibration is computed

multiple times. The results are shown in Figure. 10,

where the average of the ﬁrst N result(s) is presented

for N = 1, 2, 5, 8, and 10. The results demon-

strate that the largest translation deviation along the

X-axis is approximately 0.2 mm, and the rotational

deviation around the Y-axis is about 3 × 10

−4

radi-

ans (0.019

◦

). Given a standard deviation of approxi-

mately 0.1 × 10

−3

, using additional frames results in

nearly identical calibration performance. Therefore,

our method can reliably perform hand-eye calibration

using just a single frame of 3D point cloud data.

Figure 10: Average of the ﬁrst n calibrations at a single

pose.

In addition, different poses for eye-in-hand cali-

bration on the UR10e, as illustrated in Figure 9, are

validated. The results in Figure 11 show the maxi-

mum translation deviation was about 1.8 mm and the

minimum about 0.6 mm, with rotation deviations be-

tween 0.001 and 0.002 radians. These results demon-

strate that our proposed calibration method maintains

consistent performance across multiple poses. To-

gether with the large-scale evaluation on 14 collab-

orative robot models from 9 brands in simulation,

this conﬁrms the robustness and applicability of the

method across diverse platforms.

Figure 11: Hand-eye calibration results across 6 poses.

5 CONCLUSION AND FUTURE

WORK

In this work, we extended and improved our previ-

ous method, a 3D vision-based hand-eye calibration

approach. Our learning-based framework estimates

the pose of the robot base, enabling the computation

of the transformation matrix between the robot ﬂange

and the camera within seconds. We enhance the regis-

tration dataset by incorporating captured point clouds

from diverse perspectives and realistic robot arm con-

ﬁgurations. We conduct large-scale evaluations in-

volving 14 collaborative robot models from 9 brands,

including KUKA, ABB, and FANUC, and real-world

validation with a high-precision 3D camera on an

industrial-grade robot. These experiments conﬁrm

that our approach matches the calibration accuracy of

commercial solutions, while greatly reducing calibra-

tion time and eliminating the need for external ob-

jects, making it broadly applicable to diverse collabo-

rative robot systems.

In future work, we will focus on enhancing usabil-

ity and long-term stability to further support deploy-

ment in diverse industrial environments.

ACKNOWLEDGMENTS

The authors thank Jialong Li for his excellent col-

laboration and patient support, everyone in RobotLab

3D Hand-Eye Calibration for Collaborative Robot Arm: Look at Robot Base Once

339

LTH for their valuable assistance, and Jungner Com-

pany for its support.

REFERENCES

Allegro, D., Terreran, M., and Ghidoni, S. (2024). Multi-

camera hand-eye calibration for human-robot collab-

oration in industrial robotic workcells. arXiv preprint

arXiv:2406.11392.

Bahadir, O., Siebert, J. P., and Aragon-Camarasa, G. (2024).

Continual learning approaches to hand–eye calibra-

tion in robots. Machine Vision and Applications,

35(4):97.

Enebuse, I., Foo, M., Ibrahim, B. S. K. K., Ahmed, H.,

Supmak, F., and Eyobu, O. S. (2021). A comparative

review of hand-eye calibration techniques for vision

guided robots. IEEE Access, 9:113143–113155.

Enebuse, I., Ibrahim, B. K. K., Foo, M., Matharu, R. S., and

Ahmed, H. (2022). Accuracy evaluation of hand-eye

calibration techniques for vision-guided robots. Plos

one, 17(10):e0273261.

Ha, J. (2022). Probabilistic framework for hand–eye and

robot–world calibration ax = yb. IEEE Transactions

on Robotics, 39(2):1196–1211.

Halme, R.-J., Lanz, M., K

ainen, J., Pieters, R., La-

tokartano, J., and Hietanen, A. (2018). Review of

vision-based safety systems for human-robot collab-

oration. Procedia Cirp, 72:111–116.

Hong, I. and Ha, J. (2025). Generative adversarial networks

for solving hand-eye calibration without data corre-

spondence. IEEE Robotics and Automation Letters.

Horaud, R. and Dornaika, F. (1995). Hand-eye calibra-

tion. The international journal of robotics research,

14(3):195–210.

Hua, J. and Zeng, L. (2021). Hand–eye calibration algo-

rithm based on an optimized neural network. In Actu-

ators, volume 10, page 85. MDPI.

Huang, S., Gojcic, Z., Usvyatsov, M., Wieser, A., and

Schindler, K. (2021). Predator: Registration of 3d

point clouds with low overlap. In Proceedings of the

IEEE/CVF Conference on computer vision and pat-

tern recognition, pages 4267–4276.

Jiang, J., Luo, X., Luo, Q., Qiao, L., and Li, M. (2022).

An overview of hand-eye calibration. The Interna-

tional Journal of Advanced Manufacturing Technol-

ogy, 119(1):77–97.

Koide, K. and Menegatti, E. (2019). General hand–eye

calibration based on reprojection error minimization.

IEEE Robotics and Automation Letters, 4(2):1021–

1028.

Li, L., Yang, X., Wang, R., and Zhang, X. (2024). Auto-

matic robot hand-eye calibration enabled by learning-

based 3d vision. Journal of Intelligent & Robotic Sys-

tems, 110(3):130.

Ma, L., Bazzoli, P., Sammons, P. M., Landers, R. G., and

Bristow, D. A. (2018). Modeling and calibration of

high-order joint-dependent kinematic errors for indus-

trial robots. Robotics and Computer-Integrated Man-

ufacturing, 50:153–167.

Ma, Q., Li, H., and Chirikjian, G. S. (2016). New proba-

bilistic approaches to the ax= xb hand-eye calibration

without correspondence. In 2016 IEEE international

conference on robotics and automation (ICRA), pages

4365–4371. IEEE.

Mallon, J. and Whelan, P. F. (2007). Which pattern? bias-

ing aspects of planar calibration patterns and detection

methods. Pattern recognition letters, 28(8):921–930.

Munaro, M., Rusu, R. B., and Menegatti, E. (2016). 3d

robot perception with point cloud library.

Pachtrachai, K., Vasconcelos, F., Edwards, P., and Stoy-

anov, D. (2021). Learning to calibrate-estimating the

hand-eye transformation without calibration objects.

IEEE Robotics and Automation Letters, 6(4):7309–

7316.

Robinson, N., Tidd, B., Campbell, D., Kuli

c, D., and Corke,

P. (2023). Robotic vision for human-robot interac-

tion and collaboration: A survey and systematic re-

view. ACM Transactions on Human-Robot Interac-

tion, 12(1):1–66.

Shiu, Y. C. and Ahmad, S. (1987). Calibration of wrist-

mounted robotic sensors by solving homogeneous

transform equations of the form ax= xb.

Strobl, K. H. and Hirzinger, G. (2006). Optimal hand-eye

calibration. In 2006 IEEE/RSJ international confer-

ence on intelligent robots and systems, pages 4647–

4653. IEEE.

Tabb, A. and Ahmad Yousef, K. M. (2017). Solving the

robot-world hand-eye (s) calibration problem with it-

erative methods. Machine Vision and Applications,

28(5):569–590.

Ten Pas, A., Gualtieri, M., Saenko, K., and Platt, R. (2017).

Grasp pose detection in point clouds. The Interna-

tional Journal of Robotics Research, 36(13-14):1455–

1473.

Tsai, R. Y., Lenz, R. K., et al. (1989). A new technique for

fully autonomous and efﬁcient 3 d robotics hand/eye

calibration. IEEE Transactions on robotics and au-

tomation, 5(3):345–358.

Wang, G., Li, W., Jiang, C., Zhu, D., Li, Z., Xu, W.,

Zhao, H., and Ding, H. (2021). Trajectory planning

and optimization for robotic machining based on mea-

sured point cloud. IEEE transactions on robotics,

38(3):1621–1637.

Wang, X. and Song, H. (2024). One-step solving the hand–

eye calibration by dual kronecker product. Journal of

Mechanisms and Robotics, 16(10).

Wang, X. V., Wang, L., Mohammed, A., and Givehchi,

M. (2017). Ubiquitous manufacturing system based

on cloud: A robotics application. Robotics and

Computer-Integrated Manufacturing, 45:116–125.

Wijesoma, S., Wolfe, D., and Richards, R. (1993). Eye-

to-hand coordination for vision-guided robot control

applications. The International Journal of Robotics

Research, 12(1):65–78.

Wu, J., Liu, M., Zhu, Y., Zou, Z., Dai, M.-Z., Zhang, C.,

Jiang, Y., and Li, C. (2020). Globally optimal sym-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

340

bolic hand-eye calibration. IEEE/ASME Transactions

on Mechatronics, 26(3):1369–1379.

Zhou, P., Peng, R., Xu, M., Wu, V., and Navarro-Alarcon,

D. (2021a). Path planning with automatic seam ex-

traction over point cloud models for robotic arc weld-

ing. IEEE robotics and automation letters, 6(3):5002–

5009.

Zhou, Z., Li, L., Wang, R., and Zhang, X. (2021b). Deep

learning on 3d object detection for automatic plug-in

charging using a mobile manipulator. In 2021 IEEE

International Conference on Robotics and Automation

(ICRA), pages 4148–4154. IEEE.

Zhou, Z., Ma, L., Liu, X., Cao, Z., and Yu, J. (2023). Si-

multaneously calibration of multi hand–eye robot sys-

tem based on graph. IEEE Transactions on Industrial

Electronics, 71(5):5010–5020.

Zhu, D., Wu, H., Ding, T., and Hua, L. (2024). Point cloud

registration-enabled globally optimal hand–eye cali-

bration. IEEE/ASME Transactions on Mechatronics.

Zhuang, H., Roth, Z. S., and Sudhakar, R. (1994). Si-

multaneous robot/world and tool/ﬂange calibration by

solving homogeneous transformation equations of the

form ax= yb. IEEE Transactions on Robotics and Au-

tomation, 10(4):549–554.

Zuang, H. and Shiu, Y. C. (1993). A noise-tolerant algo-

rithm for robotic hand-eye calibration with or without

sensor orientation measurement. IEEE transactions

on systems, man, and cybernetics, 23(4):1168–1175.

3D Hand-Eye Calibration for Collaborative Robot Arm: Look at Robot Base Once

341