CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space

Through Sinusoidal Representation Networks

Christoforos Vlachos

and Konstantinos Moustakas

Department of Electrical and Computer Engineering, University of Patras, 26504 Rion-Patras, Greece

Keywords:

Conﬁguration Space Signed Distance Function (CSDF), Sinusoidal Representation Networks (SIREN), Neu-

ral Implicit Representation, Robot Conﬁguration Space, Signed Distance Function (SDF), Inverse Kinematics.

Abstract:

Signed Distance Functions (SDFs) are used in many ﬁelds of research. In robotics, many common tasks,

such as motion planning and collision avoidance use distance queries extensively and, as a result, SDFs have

been integrated widely in such tasks, fulﬁlling even the tightest speed requirements. At the same time, the

idea of the more natural representation of distances directly in the conﬁguration space (C-space) has been

gaining ground, resulting in many interesting publications in the last few years. In this work, we aim to deﬁne

a C-space Signed Distance Function (CSDF) in a way that parallels other SDF deﬁnitions. Additionally,

coupled with recent advancements in machine learning and neural representation of implicit functions, we

attempt to create a neural approximation of the CSDF in a way that is fast and accurate. To validate our

contributions, we construct an experiment environment to test the accuracy of our proposed workﬂow in an

inverse kinematics contact test. Comparing these results to the performance of another published approach to

the neural implicit representation of distances in the Conﬁguration Space, we found that our method offers a

considerable improvement, reducing the measured errors and increasing the success rate.

1 INTRODUCTION

Among the many ﬁelds of robotics, the concept of

distance has always played a critical role in the way

a robot interprets and interacts with its environment.

Whether it is used as a measurement of separation be-

tween points, obstacles, or a robot’s end effector and

its target location, it provides valuable information for

many common tasks.

Speciﬁcally regarding the ﬁeld of robotics, Signed

Distance Functions (SDFs) have been studied exten-

sively and are well-incorporated in many manipula-

tion, control, and optimization tasks. A lot of op-

erations in robotics often need to transition between

representing quantities in task-space or conﬁguration-

space (often abbreviated to “C-space”). As such, rep-

resentations of the SDF in C-space by transforming

the task-space are often used.

A different approach which, among many advan-

tages, ﬁts well in multiple common robotics work-

ﬂows, is the deﬁnition of a distance function directly

in the C-space. This function may be used instead of

https://orcid.org/0000-0003-2863-7823

https://orcid.org/0000-0001-7617-227X

the transformed task-space SDF in order to intuitively

and robustly represent the angular distance between a

robotic arm and some point in the C-space.

The learning of implicit functions has been a focal

point in many publications during the last years, ex-

hibiting remarkable results (Park et al., 2019; Milden-

hall et al., 2020; Mescheder et al., 2019). Natu-

rally, SDFs have played a major role in this oppor-

tune occasion, with many researchers opting to use

this form of implicit representation as an alternative to

explicit mesh representation, featuring important ad-

vantages (Gropp et al., 2020; Hao et al., 2020; Yariv

et al., 2021). And while neural networks for learn-

ing SDFs in the convenience of readily deﬁned Eu-

clidean spaces have been well investigated, learning

such functions directly in a robot’s C-space is a rela-

tively immature and largely uncharted subject.

Code and pretrained models of this work may be

found in the following repository: https://github.com/

ChristoforosVlachos/CSDF.git

Vlachos, C. and Moustakas, K.

CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space Through Sinusoidal Representation Networks.

DOI: 10.5220/0013736900003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 82-90

ISBN: 978-989-758-770-2; ISSN: 2184-2809

2 RELATED WORK

2.1 Implicit Representation

Although a very traditional technique, the explicit

representation of surfaces has been questioned numer-

ous times as a choice for a lot of applications. This is

especially true when we are interested in representing

continuous surfaces where a discretization of space

may prove detrimental to the task. As such, level set

methods surfaced very early on (Osher and Fedkiw,

2003; Breen and Whitaker, 1999; Bloomenthal and

Bajaj, 1997) to apply implicit functions to the com-

mon task of surface representation in ﬂuid dynamics,

modeling, as well as motion planning and robotics

jobs.

2.2 Neural Implicit Representation

Amid neural methods becoming mainstream, implicit

representations turned to leverage the neural research

that was quickly becoming the status quo. Thus, many

researchers were now using deep learning in order to

accurately and efﬁciently approximate continuous im-

plicit functions. As far as radiance ﬁelds go, NeRFs

as introduced by Mildenhall et al. (Mildenhall et al.,

2020) went on to become complete game-changers,

whereas Mescheder et al. promoted occupancy ﬁelds

for 3D shape representation (Mescheder et al., 2019).

Signed Distance Fields and Signed Distance Func-

tions played a major role in neural implicit represen-

tation. The ﬁrst major work to introduce neural SDFs

for implicitly representing 3D shapes was Park et al.’s

DeepSDF in 2019 (Park et al., 2019), competing with

Mescheder et al.’s Occupancy Networks (Mescheder

et al., 2019). Other works soon followed to improve

upon those initial concepts (Gropp et al., 2020; Or-

tiz et al., 2022), with Sitzmann et al.’s noteworthy re-

search in the use of periodic activation functions in

place of other nonlinearities to very accurately rep-

resent continuous functions (Sitzmann et al., 2020).

Those networks were nicknamed SIRENs (Sinusoidal

Representation Networks) and provide the technical

basis of our proposed workﬂow.

2.3 Signed Distance Functions in

Robotics

The concept of Signed Distance Functions was

brought over to robotics, as it seemed a natural ﬁt for

common tasks, such as collision detection/avoidance

and motion planning. Ratliff et al. (Ratliff et al., 2015)

were among the ﬁrst to use the notion of a distance

function that is negative inside an object and positive

outside to encode obstacles for motion planning in

2015. Liu et al. (Liu et al., 2022) later extended SDF-

based representations with deep learning, a concept

which led Ortiz et al. (Ortiz et al., 2022) to develop

iSDF, a real-time neural SDF approach, enabling the

use of SDFs in dynamically changing environments.

2.4 C-Space Distance Functions

While SDFs usually operate in the robot’s workspace,

an extension to this notion has been presented in the

literature that aims to express distance functions di-

rectly in the C-space, where robot motion is naturally

deﬁned. Recent work by Li et al. (Li et al., 2024a)

formalized the (unsigned) Conﬁguration space Dis-

tance Field (CDF) and used them in various applica-

tions such as inverse kinematics and motion planning.

Doing the required computations analytically though

is quite expensive.

To combat this problem, Koptev et al. (Koptev

et al., 2023) had earlier focused and experimented on

a neural representation of signed distance functions

for articulated robots. Inspired by this work, Li et

al. (Li et al., 2024a) also propose a neural extension of

their work, named the “neural-CDF” (since our work

also focuses on a neural approach, we will often omit

that part and refer to it simply as “CDF”).

3 MOTIVATION –

CONTRIBUTIONS

In the rest of this paper, we will cover a mathemat-

ical deﬁnition of a Conﬁguration Space Signed Dis-

tance Function, a complete methodology for obtain-

ing a robust neural approximation of such a function,

as well as rigorous validation and comparison in stan-

dard robotics workﬂows. Our work aims to ﬁll exist-

ing gaps in research, hoping to serve this innovative

ﬁeld of research.

Concisely, our contribution focuses on the follow-

ing items:

• formalize the deﬁnition of a Conﬁguration Space

Signed Distance Function (CSDF) as a mathemat-

ical quantity and ﬁt it inside the distance functions

spectrum.

• deﬁne a methodology to enable the creation of a

neural structure to obtain the CSDF quickly and

accurately. Similar structures have yet to be de-

ployed and examined in such high dimensional

environments.

• improve upon existing relevant solutions in terms

of speed, memory requirements, and ﬁdelity.

CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space Through Sinusoidal Representation Networks

4 METHODS

4.1 Background

A distance function is usually deﬁned as a scalar func-

tion f (x) that represents the (minimum) distance be-

tween point x and a second object. This deﬁnition

holds, even when x ∈ R

and n > 3.

In the case of the SDF, φ(x), it is commonly ex-

pressed as:

φ(x) =











0 , x ∈ ∂Ω

d(x), x ∈ Ω

−d(x), x ∈ Ω

−

, (1)

where Ω ⊆ R

and ∂Ω represents an airtight boundary

iso-surface splitting Ω into Ω

(the part of the space

outside the iso-surface) and Ω

−

(the part of the space

enclosed by the iso-surface). d(x) then represents the

distance between x and the nearest point of ∂Ω. The

negative sign is given to Ω

−

by convention.

While the concept of the SDF is often seen and

used in a multitude of manners and in various prob-

lems of robotics, a new form of distance functions, the

C-space Distance Functions, is gaining ground. Even

though our human intuition processes perfectly Eu-

clidean robot workspaces well, to a robot the (usually

non-Euclidean) C-space is a much more intuitive en-

vironment where its operations can be deﬁned easily,

even naturally. To this extent, the collection of dis-

tance functions may be broadened to contain

(x) =











0 , x ∈ ∂Ω

(x), x ∈ Ω

−d

(x), x ∈ Ω

−

, (2)

where d

represents distance in C-space, which may

be geodesic, angular, or a combination of the two.

Here ∂Ω

is, again, a boundary surface splitting Ω

into an outside region Ω

and an inside region Ω

−

Ω

may be chosen to be a subset of the C-space or it

may not; this detail is heavily inﬂuenced by the con-

ditions of the relevant task.

It should be emphasized that Equation 2 is no dif-

ferent than Equation 1. It is only a speciﬁc case ex-

pressed formulaically for clarity. This is in contrast to

simply applying a transformation to an existing SDF

deﬁned in the robot’s workspace to be expressed in

the domain of its C-space, as is very well demon-

strated in (Li et al., 2024a). Moreover, the CSDF is

similarly distinct from its unsigned counterpart intro-

duced in the same work in that a CSDF is not merely a

sub-category of SDF – it is an SDF, deﬁned in a space

where distance is measured geodesically.

One more point of note is that, when talking in

terms of the CSDF (or, likewise, the SDF) of a robot,

this function is modiﬁed as the robot navigates its

workspace. Therefore, we should rewrite the CSDF

in the form φ

(p, q), expressing it relative to both the

query point p ∈ R

and the robot’s current conﬁgura-

tion q ∈ R

, with n representing the dimensionality

of the workspace (normally, 2 or 3) and m being the

number of Degrees-of-Freedom of the robot in use.

With our proposed approach, the neural repre-

sentation of the CSDF φ

(p, q) is equivalent to the

representation of the distance function φ

(x), when

x = [p, q] and x ∈ R

(n+m)

(in other words, here we set

Ω

⊆ R

(n+m)

). This approach exposes the problem of

the CSDF representation to be completely analogous

to that of representing any SDF of possibly high di-

mensionality n + m – and it should be treated as such.

4.2 Neural Implicit Representation

We are interested in obtaining an approximation of

(p, q), which we call

(p, q), by neural network.

There are many possibilities for the choice of archi-

tecture that have appeared in literature (Park et al.,

2019; Gropp et al., 2020), each with their own ad-

vantages, prevalent features, and areas of expertise.

One speciﬁc architecture, namely the Sinusoidal Rep-

resentation Network (SIREN) (Sitzmann et al., 2020),

has demonstrated great results in the representation

of continuous signals (including SDFs) (Vlachos and

Moustakas, 2024) and appears very well suited for the

task at hand.

SIRENs, to be concise, are comprised of a few

fully connected NN layers. They differ from usual

MLPs in that they employ sinusoidal activation func-

tions instead of opting for the usual nonlinearities

(ReLU, tanh, etc.). While their usefulness has been

demonstrated in tasks of generally low dimensional-

ity, they are yet to be tested in high dimensionality

problems, as is the approximation of the CSDF.

We constructed a SIREN consisting of 1 input, 1

output, and 3 hidden layers. This distribution of layers

is common in literature and usually obtained the best

results in our own testing. The input layer consists of

(n + m) neurons to input the query point p ∈ R

and

current robot conﬁguration q ∈ R

, while the output

layer contains only a single neuron to output the value

of the predicted CSDF,

(p, q). Different amounts of

neurons for the hidden layers were investigated. Two

variants are showcased here, one with 512 neurons per

hidden layer, and a lighter one, with 256 neurons per

hidden layer. The architecture of our proposed SIREN

solution can be examined in Figure 1.

To aid the SIREN in its difﬁcult task of approxi-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

SDF

query coordinates

3 hidden layers

robot configuration

Figure 1: The architecture of our proposed SIREN for a qual-

ity approximate representation of the C-Space Signed Dis-

tance Function (CSDF).

mating the CSDF, an appropriate loss function must

be deployed. Based on previously published litera-

ture of similar tasks (Li et al., 2024a; Sitzmann et al.,

2020), we constructed the following loss function:

csd f

= w

Ω

∥|∇

(p, q)| − 1∥dx

+ w

Ω

(1 − ⟨∇

(p, q), ∇

(p, q)⟩)dx

+ w

Ω

(p, q) − φ

(p, q)|dx

+ w

Ω

∥∇

(p, q)∥

(3)

In Equation 3, the ﬁrst integral enforces the, so

called, eikonal equation on the entire space Ω

. Be-

ing a distance function, for the CSDF it is fundamen-

tal that ∥∇

(x)∥ = 1 almost everywhere (except for

a few degenerate points (Osher and Fedkiw, 2003)).

The second integral is a classic cosine similarity loss

which ensures that the predicted CSDF has a similar

direction with the ground-truth CSDF.

The third integral is a direct comparison of the pre-

dicted function to the ground-truth values. There is

a key distinction between this term and the one sug-

gested by (Li et al., 2024a): instead of minimizing

distance errors using the L2 norm, we use the L1

norm (absolute difference). This subtle change leads

to improved accuracy and stability, preventing exces-

sive error penalization and ensuring smoother conver-

gence. In high-dimensional C-space representations,

our approach mitigates the disproportionate inﬂuence

of large errors seen with L2-based losses, resulting in

a more precise CSDF approximation.

A fourth integral may be optionally added in order

to curb the second-order derivatives of the predicted

function, maintaining smooth changes. We identiﬁed

this term as a viable regularization option by our own

ablation experiments and observed a measurable im-

provement when using it.

Studying the proposed loss function, since the sec-

ond and third integral terms require knowledge of the

ground truth CSDF, φ

(p, q), it is immediately evi-

dent that the calculation of the ground truth CSDF, at

least for select samples to be used as input data will

be unavoidable. For lower dimensionality distance

functions, we might have evaded using different loss

terms that do not require knowledge of the ground-

truth CSDF, leveraging insightful heuristics, similar

to (Sitzmann et al., 2020). Here, such a simpliﬁcation

is likely not possible. In the following experiments,

the weights of the individual loss terms were set to

= 0.01, w

= 0.1, w

= 5.0, and w

= 0.01, as

per the existing literature (Li et al., 2024a). These

ensure a good match with the available ground truth

data, while also using less enforced terms to assist in

regularization.

5 EXPERIMENTS

To assess the performance of our proposed solution,

both in terms of accuracy and speed, we simulated

an environment where a single 7-DoF Franka Emika

robotic arm was tasked to make contact with one spe-

ciﬁc point in the robot’s 3D task space.

As ground truth data, we followed the dataset gen-

eration instructions in (Li et al., 2024a). They were

obtained by creating a sampling grid of dimensions

20×20×20 from the robot’s workspace and, through

optimization techniques, ﬁnding the conﬁgurations q

′

that satisfy φ(p, q

′

) = 0 for each point p in the grid.

φ(p, q) represents the SDF model of the robot i.e., a

function that is able to represent the signed distance

of point p to the robot in conﬁguration q. This kind of

problem has been tackled before (Koptev et al., 2023;

Liu et al., 2022). We made use of the SDF model pub-

lished in (Li et al., 2024b) in order to compete with

neural-CDF (Li et al., 2024a) in a fair manner.

As far as the implementation of the contact task is

concerned, we adopt the following process. By cal-

culating

(p, q

i−1

) = d

at each iteration i, we deter-

mine the appropriate movement as:

∆q

= −

(p, q

i−1

) × ∇

(p, q

i−1

) (4)

and, consequently, q

= q

i−1

+ ∆q

. The derivative is

calculated by auto-differentiation.

If the solution works well, it is expected that q

would converge to a conﬁguration q

′

with the property

that φ(p, q

′

) = 0. Therefore, after each iteration step,

φ(p, q

) is calculated and this function’s magnitude is

CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space Through Sinusoidal Representation Networks

regarded as error. For increased precision in testing,

we repeat this test for 1000 pairs of points p and ini-

tial conﬁgurations q

. As metrics, we report the mean

average error (MAE) and the root mean square error

(RMSE). The success rate (SR) is also reported as an-

other metric and is deﬁned as the percentage of con-

ﬁgurations q

that were sufﬁciently close to the target

point p, less than 3 cm away.

6 RESULTS

Li et al. (Li et al., 2024a) have recently worked on

C-Space Distance Fields, presenting a similar method

for obtaining a neural representation of the (unsigned)

C-Space Distance Function using a simple MLP en-

hanced by positional encoding. Although our ap-

proach targets a similar representation, our individ-

ual methods differ signiﬁcantly in many important

details. Thus, we consider this a suitable method to

compare our solution to, highlighting the value those

details carry.

Our proposed SIREN network consists of 3 hidden

layers of 512 neurons per layer. On the input side, the

3 cartesian coordinates of the query point are passed

to the network, along with the 7 joint angles of the

robotic arm (matching the 7 Degrees of Freedom of

the Franka Emika), giving us an input dimension of 3

+ 7 = 10.

We are also proposing and testing a lighter version

of the above SIREN (“SIREN light”), one with only

256 neurons per hidden layer. This is done in order to

push the SIREN architecture to its limit and assess its

potential.

Each network was trained for 50 000 epochs on an

AWS “g5.xlarge” instance featuring a single NVidia

A10G Tensor Core GPU with 24 GB of VRAM and

4 vCPUs on a system with 16 GB of RAM. On each

epoch, 20 000 points were sampled from the dataset,

along with 100 conﬁgurations per query point, total-

ing a batch size of 20 000 × 100.

After training, each network was tested on the

contact experiment. For each test, the number of it-

erations the network was allowed in order to manage

contact was kept ﬁxed. The results of these experi-

ments may be found on Table 1. Reported are means

and variances of the relevant metrics obtained by re-

peating each test 100 times. A few sample iterations

may be seen rendered in Figure 2.

Looking at Table 1, we notice that the CDF ap-

proach (MLP with positional encoding) gives a poor

success rate after the ﬁrst iteration, and signiﬁcantly

better results afterwards, reaching its peak perfor-

mance after 5 iterations. In contrast, using our pro-

Figure 2: Four rendered frames from the contact experi-

ments. In each run, the Franka Emika robot is tasked with

making contact with a speciﬁc point inside its task space (a

small, colored sphere is used to represent said point) but has

only a set amount of C-space moves to get there. It is ob-

served and validated that contact is apparently achieved.

posed SIREN, we achieve adequate results after the

ﬁrst iteration already. By the second iteration, we

have honed the success rate to 93.8%, 2% better than

CDF ever managed. At the third iteration, the suc-

cess rate rises to its peak: 95.4%. Even our proposed

“SIREN light” variant hits consistently lower errors

and a higher success rate than CDF.

SIRENS are known for converging very fast and

with little data to an accurate solution. In order to

let our approach truly demonstrate its potential, we

chose to repeat the experiment, this time training each

network on a way smaller batch size of 10 points ×

100 conﬁgurations, for 50 000 epochs too. Then, a

repeat of the contact task was performed, providing

the results of Table 2.

This time, we notice that the CDF method fails

to produce decent results, struggling to reach a 78%

success rate even after 5 iterations. On the other

hand, our proposed SIREN for approximating the

CSDF achieves great results after only 2 iterations.

With further adjustment iterations, the success rate

reaches 90.7%. The “SIREN light” follows the same

story, trailing closely behind “SIREN” and managing

a plateau of 90% success rate.

Another dimension of the problem, which we have

yet to discuss is the ofﬂine training time of each rep-

resentation, as well as the number of trainable param-

eters, which directly inﬂuences the memory require-

ments. For the experiments that were performed, a

collection of these measurements can be seen on Ta-

ble 3. It should be noted that all the improvements that

were achieved by our method, were attained with less

training time on a representation utilizing fewer pa-

rameters. It is also worth pointing out that our testing

suggested that the large training time of the full SIREN

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

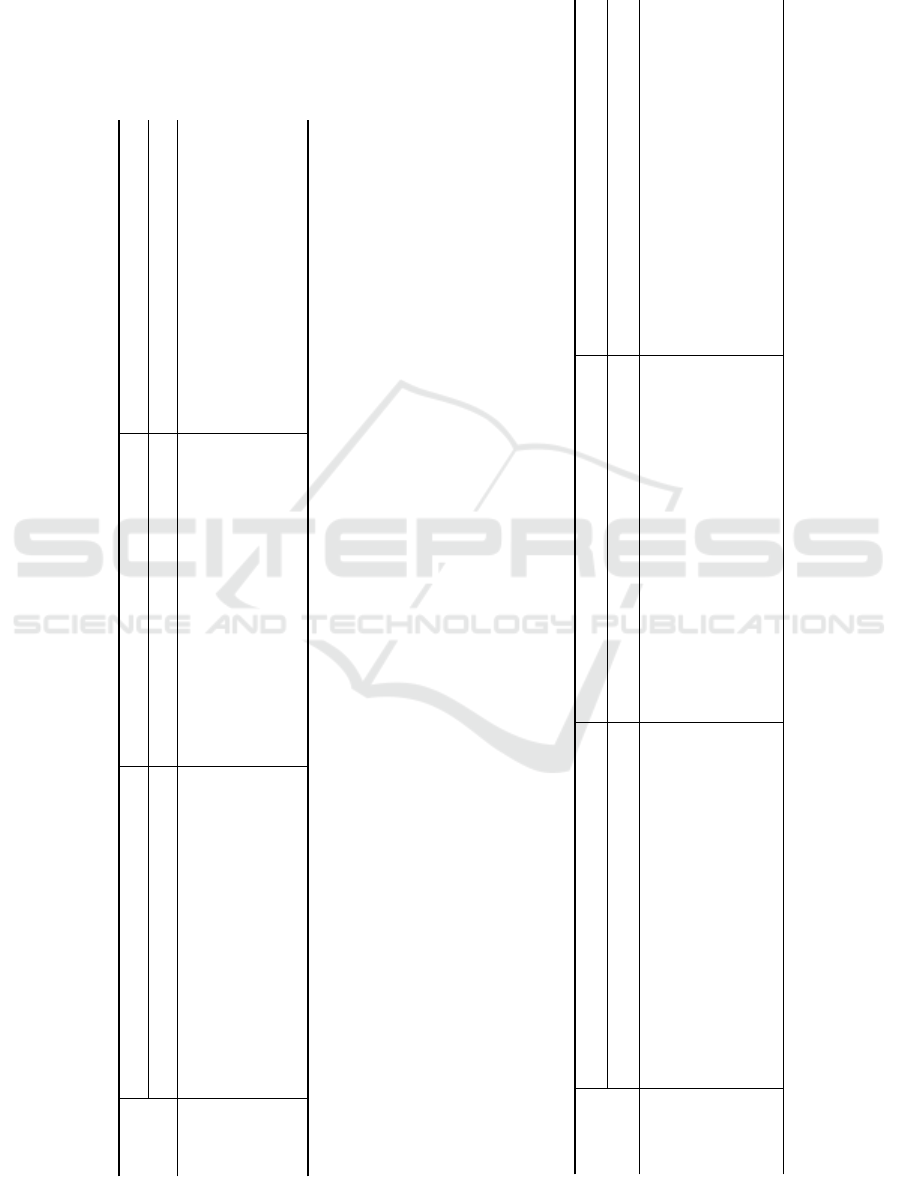
Table 1: Results of the contact experiment. Calculation

of the C-space distances and gradients is performed by

CDF (Li et al., 2024a), our SIREN-based approach for

CSDF, and by a lighter version of the same network. All

networks were trained on a batch size of 20000 × 100 for

50000 epochs. Results after 1, 2, 3, 4, 5, or 10 iterations

are displayed. For Mean Average Error (MAE) and Root

Mean Squared Error (RMSE), lower is better. For Success

Rate (SR), higher is better.

Projection

Iterations

CDF SIREN SIREN light

MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑

1 5.01 ± 1.87 8.62 ± 3.12 59.8 ± 12.1 4.61 ± 1.94 8.91 ± 3.75 70.2 ± 10.3 5.03 ± 2.06 9.46 ± 3.82 67.6 ± 9.8

2 1.66 ± 0.59 2.81 ± 1.19 87.5 ± 9.0 1.38 ± 0.43 2.78 ± 1.24 93.8 ± 5.6 1.46 ± 0.47 3.03 ± 1.37 93.1 ± 4.8

3 1.37 ± 0.50 2.02 ± 0.84 91.2 ± 8.6 1.17 ± 0.34 1.73 ± 0.67 95.4 ± 5.0 1.21 ± 0.37 1.79 ± 0.71 95.0 ± 5.3

4 1.37 ± 0.54 1.95 ± 0.85 91.4 ± 9.0 1.20 ± 0.38 1.61 ± 0.55 94.9 ± 6.2 1.22 ± 0.41 1.66 ± 0.71 94.6 ± 7.2

5 1.36 ± 0.53 1.91 ± 0.84 91.7 ± 8.7 1.24 ± 0.41 1.66 ± 0.60 94.2 ± 6.6 1.27 ± 0.44 1.72 ± 0.76 93.5 ± 7.7

10 1.37 ± 0.55 1.91 ± 0.82 91.2 ± 8.9 1.33 ± 0.49 1.75 ± 0.78 93.4 ± 8.0 1.34 ± 0.55 1.81 ± 1.00 93.1 ± 8.4

Table 2: Results of the contact experiment, similar to Ta-

ble 1. All networks were trained on a batch size of 10 ×100

for 50000 epochs.

Projection

Iterations

CDF SIREN SIREN light

MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑

1 7.86 ± 2.73 11.48 ± 3.93 39.5 ± 12.2 6.69 ± 2.75 11.00 ± 4.24 53.4 ± 13.1 7.33 ± 3.04 11.73 ± 4.49 50.4 ± 12.7

2 2.98 ± 1.07 4.79 ± 1.66 69.8 ± 12.4 1.94 ± 0.76 3.79 ± 1.62 85.9 ± 9.3 2.17 ± 0.83 4.25 ± 1.81 83.5 ± 9.5

3 2.23 ± 0.92 3.38 ± 1.36 77.8 ± 13.2 1.47 ± 0.57 2.32 ± 1.06 90.4 ± 8.0 1.58 ± 0.53 2.58 ± 1.04 88.7 ± 8.1

4 2.18 ± 0.86 3.20 ± 1.26 77.8 ± 13.5 1.42 ± 0.58 2.07 ± 0.93 90.7 ± 8.1 1.47 ± 0.54 2.17 ± 0.93 90.0 ± 8.1

5 2.19 ± 0.93 3.20 ± 1.43 77.9 ± 14.0 1.41 ± 0.49 2.02 ± 0.84 90.7 ± 7.9 1.51 ± 0.60 2.19 ± 1.01 89.3 ± 9.1

10 2.31 ± 1.01 3.29 ± 1.43 75.5 ± 14.8 1.46 ± 0.64 2.09 ± 1.15 90.4 ± 9.3 1.57 ± 0.72 2.23 ± 1.20 88.4 ± 11.2

CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space Through Sinusoidal Representation Networks

Table 3: Training time for 50000 epochs and number of trainable parameters for the neural-CDF network (Li et al., 2024a),

for our SIREN-based approach, and for the lighter version of the same network.

Batch Size Approach Training Time Trainable Parameters

20000 CDF 5:37:13 737 409

× SIREN 5:53:40 531 457

100 SIREN light 4:17:30 134 657

10 CDF 2:15:44 737 409

× SIREN 1:33:33 531 457

100 SIREN light 1:34:14 134 657

approach at a large batch size was likely caused by a

memory fragmentation issue in our system. Further-

more, no decrease in training time is observed using

the light variant over the full SIREN variant for the

smaller batch size, as for a batch size this small the

training operations take severely less time and hard-

ware overheads come heavily into play. Although this

means that training may take less time on different

systems, the fact that such issues can occur should be

kept in mind when implementing any of the discussed

methods.

Ultimately, it is important to note that, evidently,

the “light” variant of our proposed workﬂow is likely

the most desirable middle ground in terms of accu-

racy, training time, and memory requirements. In or-

der to squeeze out that last bit of a accuracy, one may

use our full-sized SIREN workﬂow. Either way, our

proposed solutions far outperform the alternatives.

7 CONCLUSION AND FUTURE

WORK

We have clearly and robustly deﬁned the C-space

Signed Distance Function (CSDF) as a form of a

SDF. We have posed the problem of representing an

implicit function, such as the CSDF, utilizing recent

advancements in neural implicit representation and

work on C-space Distance Functions. We have pro-

posed a methodology for creating a neural approxima-

tion and implemented two variations of our proposed

method. We have set up an experiment to validate and

compare our method to another recently published ap-

proach tackling the same problem and found that our

method of representing the CSDF easily outperforms

the alternative.

In the future we aim to reﬁne our approach with

more rigorous experimentation across many scenarios

and between different methods. Our very promising

results indicate that, provided a careful approach is

taken, this method can offer robust solutions to many

problems in the general ﬁeld of robotics, such as mo-

tion planning and inverse kinematics. Speciﬁcally,

details such as the loss function should be investigated

further, as, while most of the literature agrees on the

fundamental parts, some details are left to be settled.

ACKNOWLEDGMENTS

The research project is implemented in the framework

of H.F.R.I. call “Basic research Financing (Horizontal

support of all Sciences)” under the National Recovery

and Resilience Plan “Greece 2.0” funded by the Eu-

ropean Union – NextGenerationEU (H.F.R.I. Project

Number: 16469).

REFERENCES

Bloomenthal, J. and Bajaj, C. (1997). Introduction to im-

plicit surfaces. Morgan Kaufmann.

Breen, D. E. and Whitaker, R. T. (1999). A level-set ap-

proach for the metamorphosis of solid models. In

ACM SIGGRAPH 99 Conference abstracts and appli-

cations, SIGGRAPH99, page 228. ACM.

Gropp, A., Yariv, L., Haim, N., Atzmon, M., and Lipman, Y.

(2020). Implicit geometric regularization for learning

shapes. In 37th International Conference on Machine

Learning, ICML 2020, pages 3747–3757.

Hao, Z., Averbuch-Elor, H., Snavely, N., and Belongie, S.

(2020). Dualsdf: Semantic shape manipulation us-

ing a two-level representation. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition.

Koptev, M., Figueroa, N., and Billard, A. (2023). Neural

joint space implicit signed distance functions for re-

active robot manipulator control. IEEE Robotics and

Automation Letters, 8(2):480–487.

Li, Y., Chi, X., Razmjoo, A., and Calinon, S. (2024a). Con-

ﬁguration space distance ﬁelds for manipulation plan-

ning. In Robotics: Science and Systems XX, RSS2024.

Robotics: Science and Systems Foundation.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

Li, Y., Zhang, Y., Razmjoo, A., and Calinon, S. (2024b).

Representing robot geometry as distance ﬁelds: Ap-

plications to whole-body manipulation. In 2024 IEEE

International Conference on Robotics and Automation

(ICRA), page 15351–15357. IEEE.

Liu, P., Zhang, K., Tateo, D., Jauhri, S., Peters, J., and

Chalvatzaki, G. (2022). Regularized deep signed

distance ﬁelds for reactive motion generation. In

2022 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS). IEEE.

Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S.,

and Geiger, A. (2019). Occupancy networks: Learn-

ing 3d reconstruction in function space. In 2019

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition (CVPR). IEEE.

Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T.,

Ramamoorthi, R., and Ng, R. (2020). NeRF: Rep-

resenting Scenes as Neural Radiance Fields for View

Synthesis, page 405–421. Springer International Pub-

lishing.

Ortiz, J., Clegg, A., Dong, J., Sucar, E., Novotny, D., Zoll-

hoefer, M., and Mukadam, M. (2022). isdf: Real-

time neural signed distance ﬁelds for robot perception.

In Robotics: Science and Systems XVIII, RSS2022.

Robotics: Science and Systems Foundation.

Osher, S. and Fedkiw, R. (2003). Level Set Methods and

Dynamic Implicit Surfaces. Springer New York.

Park, J. J., Florence, P., Straub, J., Newcombe, R., and

Lovegrove, S. (2019). Deepsdf: Learning continuous

signed distance functions for shape representation. In

2019 IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR), page 165–174. IEEE.

Ratliff, N., Toussaint, M., and Schaal, S. (2015). Under-

standing the geometry of workspace obstacles in mo-

tion optimization. In 2015 IEEE International Con-

ference on Robotics and Automation (ICRA), page

4202–4209. IEEE.

Sitzmann, V., Martel, J., Bergman, A., Lindell, D., and Wet-

zstein, G. (2020). Implicit neural representations with

periodic activation functions. Advances in neural in-

formation processing systems, 33:7462–7473.

Vlachos, C. and Moustakas, K. (2024). High–ﬁdelity hap-

tic rendering through implicit neural force representa-

tion. In International Conference on Human Haptic

Sensing and Touch Enabled Computer Applications,

pages 493–506. Springer.

Yariv, L., Gu, J., Kasten, Y., and Lipman, Y. (2021). Vol-

ume rendering of neural implicit surfaces. Advances

in Neural Information Processing Systems, 34:4805–

4815.

APPENDIX

During the initial stages of the presented research,

a debate in the literature between signed and un-

signed distance functions and their advantages, made

us wonder whether choosing a signed representation

was the better option. While a signed representation

was more intuitive to us and we felt that the continu-

ous derivatives was a very attractive feature, unsigned

CDFs had been successfully used already. After care-

ful testing, the signed representation appeared as a

more robust and stable option for our use cases. It

is worth mentioning that under certain circumstances

using an unsigned representation might be desirable,

if one is willing to sacriﬁce stability for marginally

higher peaks. For the sake of completeness, results for

an unsigned C-space Distance Function represented

using the same SIRENs are included in Table 4 for the

batch size of 20000 × 100 and Table 5 for the batch

size of 10 × 100. These may be directly compared to

the results of Table 1 and Table 2, respectively. Ad-

ditionally, Table 6 serves as an expansion to Table 3

that includes training time for the unsigned cases.

Table 4: Additional results of the contact experiment. Calculation of the C-space distances and gradients is performed by an

unsigned variant of our SIREN-based approach, and by a lighter version of the same network. Both networks were trained on

a batch size of 20000 × 100 for 50000 epochs. Results after 1, 2, 3, 4, 5, or 10 iterations are displayed. For Mean Average

Error (MAE) and Root Mean Squared Error (RMSE), lower is better. For Success Rate (SR), higher is better.

Projection

Iterations

SIREN (unsigned) SIREN light (unsigned)

MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑

1 4.58 ± 1.80 8.97 ± 3.49 70.5 ± 9.7 4.94 ± 1.93 9.25 ± 3.64 67.5 ± 10.0

2 1.37 ± 0.46 2.78 ± 1.19 93.9 ± 6.3 1.46 ± 0.45 2.99 ± 1.26 93.0 ± 5.8

3 1.15 ± 0.34 1.68 ± 0.63 95.6 ± 4.6 1.20 ± 0.35 1.75 ± 0.65 95.3 ± 5.5

4 1.23 ± 0.41 1.65 ± 0.66 94.6 ± 6.9 1.22 ± 0.37 1.63 ± 0.60 94.5 ± 5.8

5 1.27 ± 0.45 1.71 ± 0.75 93.9 ± 7.8 1.24 ± 0.40 1.65 ± 0.59 93.8 ± 6.6

10 1.37 ± 0.54 1.86 ± 0.91 92.8 ± 8.1 1.34 ± 0.52 1.75 ± 0.78 92.8 ± 9.2

CSDF-by-SIREN: Learning Signed Distances in the Conﬁguration Space Through Sinusoidal Representation Networks

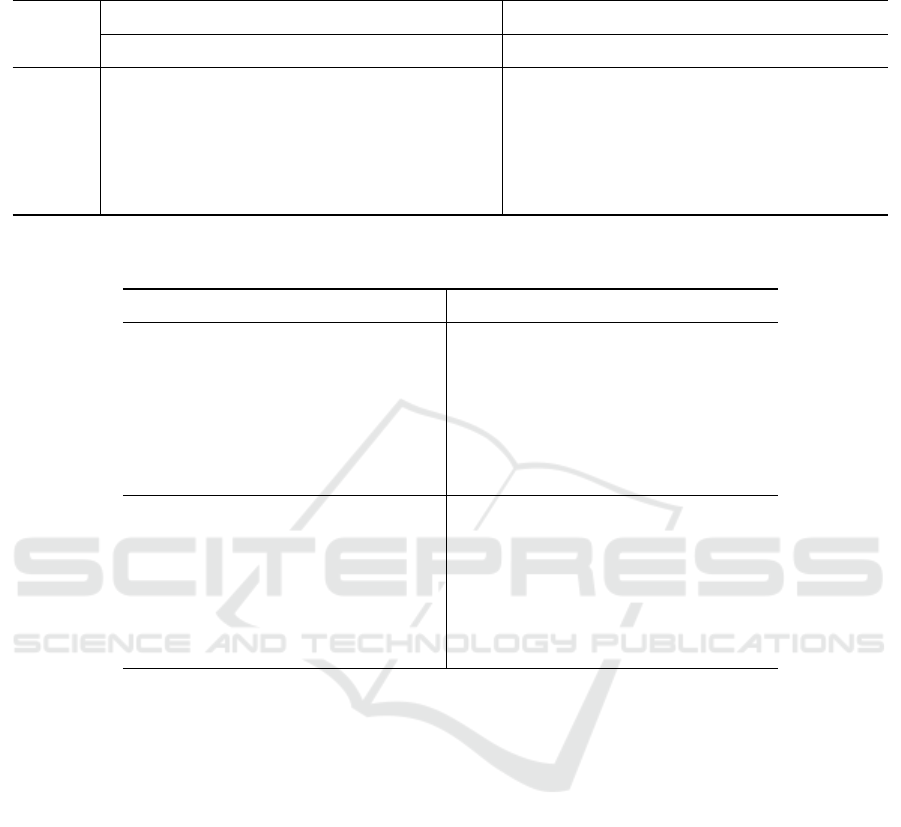
Table 5: Additional results of the contact experiment, similar to Table 4. Both networks were trained on a batch size of

10 × 100 for 50000 epochs.

Projection

Iterations

SIREN (unsigned) SIREN light (unsigned)

MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑ MAE (cm) ↓ RMSE (cm) ↓ SR (%) ↑

1 6.76 ± 2.62 11.11 ± 4.12 52.8 ± 12.2 7.20 ± 2.97 11.64 ± 4.46 51.5 ± 13.1

2 1.87 ± 0.73 3.58 ± 1.56 86.5 ± 8.8 2.05 ± 0.84 3.93 ± 1.77 84.7 ± 9.4

3 1.45 ± 0.59 2.26 ± 1.00 90.5 ± 8.1 1.58 ± 0.64 2.51 ± 1.10 88.5 ± 9.4

4 1.39 ± 0.48 1.98 ± 0.77 91.2 ± 7.6 1.49 ± 0.53 2.17 ± 0.94 89.4 ± 8.4

5 1.40 ± 0.54 1.99 ± 0.92 91.0 ± 8.2 1.54 ± 0.62 2.23 ± 1.04 88.8 ± 9.4

10 1.46 ± 0.55 2.09 ± 1.07 90.0 ± 8.9 1.65 ± 0.84 2.36 ± 1.36 87.4 ± 11.9

Table 6: Expanded form of Table 3 to include an unsigned variant of our SIREN-based approach and a lighter version of the

same network. Training time is measured for 50000 epochs.

Batch Size Approach Training Time Trainable Parameters

20000

CDF 5:37:13 737 409

SIREN 5:53:40

531 457

× SIREN (unsigned) 5:41:46

100

SIREN light 4:17:30

134 657

SIREN light (unsigned) 4:09:08

CDF 2:15:44 737 409

SIREN 1:33:33

531 457

× SIREN (unsigned) 1:32:05

100

SIREN light 1:34:14

134 657

SIREN light (unsigned) 1:32:52

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics