Performance Analysis and Improvement of Double Circuit EHV AC

Transmission Lines by Increasing Surge Impedance Loading Level

Jitendra G. Jamnani

and Varun Patel

School of Energy Technology, Pandit Deendayal Energy University, Gandhinagar, Gujarat, India

Keywords: SIL (Surge Impedance Loading), Bundle Spacing, EHV (Extra High Voltage) AC Transmission, Expanded

Hexa, Delta Configuration, Hexagon Configuration.

Abstract: The demand of Electrical Energy is continuously increasing due to the growth of society and industrialization

and to fulfil this requirement, increase in power generation and its transmission at high efficiency is required.

Extra high voltages are necessary to transfer large amount of power over linger distances as the power transfer

limit is proportional to the square of rated voltage. Generally the power generating stations are far away from

the distribution network and to connect the power surplus region to power deficit region we need long EHV

AC double circuit transmission lines to carry large amount of power. But the long EHV AC transmission lines

are limited by their SIL (Surge Impedance Loading) limit which is much below the thermal limit of conductor

due to large inductive reactance of the line. SIL depends on various factors and geometrical arrangement of

double circuit transmission lines i.e. bundle spacing, size of conductor, number of sub-conductors per phase,

etc. This paper presents various methodologies to improve SIL level of EHV AC lines and also its effect on

corona loss. MATLAB is used as platform for development of GUI based software to calculate and analyze

the various parameters related to SIL and corona loss. The various double circuit configurations used for EHV

AC transmission lines and its comparison is also presented.

1 INTRODUCTION

Extra high voltages are necessary for transfer of large

amount power over longer distances. To transfer

more power, higher transmission voltage is

necessary. Power transfer limit is proportional to the

square of rated voltage. For the same power transfer,

the line losses reduce with higher rated voltage due to

reduction in current. With higher Transmission

Voltage, conductor size requirement is reduced.

Therefore conductor cost will reduce. To transfer

large amount of power from power surplus region or

state to power deficit states or region requires long

EHV AC transmission lines. However long EHV AC

transmission lines are limited by SIL (Surge

Impedance Loading) / Stability limits due to large

inductance of the lines(Nayak, Sehgal, et al. , 2022),

(Daconti and Daniel, 2023).

https://orcid.org/0000-0001-6238-1222

2 SURGE IMPEDANCE

LOADING (SIL) AND CORONA

LOSS

SIL is the MW loading of the line where natural

reactive power balance occurs i.e. reactive power

produced by a line is equal to reactive power

consumed by a line. If we load the line above SIL the

line would consume reactive power and limits the

power transfer capacity to maintain stability of the

system.

The surge impedance loading concept is suitable

for EHV AC lines to decide the MW loading and

corresponding voltage variation along the line length.

To increase SIL level, line inductance is to be reduced

and /or capacitance is to be increased. (Hao and Xu,

2022), (Kishore, Singal, et al. , 2021), (Siva, Rani, et

al. , 2020)

Corona is formed due to ionisation of air

surrounding the conductors. The formation of corona

is always accompanied by Energy loss which is

Jamnani, J. G. and Patel, V.

Performance Analysis and Improvement of Double Circuit EHV AC Transmission Lines by Increasing Surge Impedance Loading Level.

DOI: 10.5220/0013734200004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 3, pages 871-876

ISBN: 978-989-758-763-4

871

dissipated in the form of light, heat, sound and

chemical action. When corona occurs, it produces

loss of power. For calculation of SIL,

SIL =







, where Zs is surge impedance and is

given by

Zs =







and inductance L is given by

L = Ls–Lm

Ls = self-inductance of line=2* 10



𝑙𝑛





H/m

Lm = mutual inductance of the line=2* 10



𝑙𝑛





H/m

Where GMD is geometric mean distance between

conductors and GMR is the geometric mean radius of

conductor.

For calculation of corona, the foul weather

condition is selected which is worst. So the formula

used to calculate corona is Project EHV, USA by

Anderson, Baretsky and McCarthy Formula.

Pc = Pfw + 0.3606 k. V. 𝑟



.ln (1+10ρ).

∑

𝐸







Where,

Pc = Foul weather corona loss

Pfw = total fair weather corona loss = 1 to 5

kw/km for 500 kV and 3 to 20kw/km for 700kV,

for calculation of 400kV line Pfw is taken as 5

kw/km.

K = 7.04 * 10



for 400kV (based on Rheinau

results)

V = conductor voltage in kV, l-l r.m.s

E = surface voltage gradient on the underside of

the conductor, kV/cm, peak

ρ = rain rate in mm/hr, taken as 5mm/hr

r = radius of conductor in cm

N = no. of sub conductors in bundle of each phase

Voltage gradient is calculated using standard

mangoldt’s formula.

3 METHODOLOGIES TO

INCREASE SURGE

IMPEDANCE LOADING LEVEL

CONSIDERING CORONA LOSS

For long transmission lines the power transfer

capacity is limited by its SIL level only which is much

below its thermal capacity due to large inductance.

Also Decrease in line inductance and surge

impedance shall increase the SIL and transmission

capacity.

The surge impedance loading (SIL) depends on

many factors such as (a) phase spacing (b) Bundle

spacing (c) size of conductor (d) number of sub-

conductors per phase and (e) conductor

configurations. In this research paper, for a particular

data of 400kV double circuit transmission line

configurations, the effect of Bundle spacing, size of

conductor, Number of sub-conductors per phase,

Horizontal and vertical spacing on SIL level and

corona loss is presented and hence to improve the

power transmission capacity.

MATLAB is used as platform for development of

GUI based software to calculate and analyze the

various parameters related to SIL and corona loss.

The various double circuit configurations used for

EHV AC transmission lines and its comparison is also

presented.

The above methods have been analyzed and

discussed for 400kV Double circuit transmission line

and there result tables and graphs showing its effect

on SIL and Corona loss has been presented. The

parameters used to obtain the results have been shown

in the graph itself

. (Sakhavati, Yaltagiani, et al. , 2020),

(Begamudre, 2020), (Saadat, 2020), (Dritsas, Alexiou, et al.

, 2022), (Gupta, Saha, et al. , 2021)

3.1 Bundle Spacing (B)

Bundle spacing is the spacing between sub-

conductors, as the B increases Bundle radius R

increases and GMReq of bundled conductor

increases, which leads to reduction in self-inductance

of the line and we can have reduction in line

inductance and increase in SIL level as the B

increases. However the corona loss would slightly

increase with increase in bundle spacing but

comparative to that there is large increment in SIL

level is obtained. The Table 1 and Figure 1 show the

effect of change in bundle spacing on SIL and corona

loss.

Table 1: Bundle Spacing (B) in cm v/s SIL and Corona

(cm

)

L(mH/k

C(nF/k

SIL

(MW)

Pc(kw/3phas

e km)

35 0.389 29.05 1382.65 11.55

40 0.379 29.84 1419.48 11.76

45 0.37 30.56 1453.63 12.04

50 0.362 31.24 1485.0 12.37

55 0.355 31.88 1515.77 13.13

60 0.349 32.48 1544.39 13.55

INCOFT 2025 - International Conference on Futuristic Technology

872

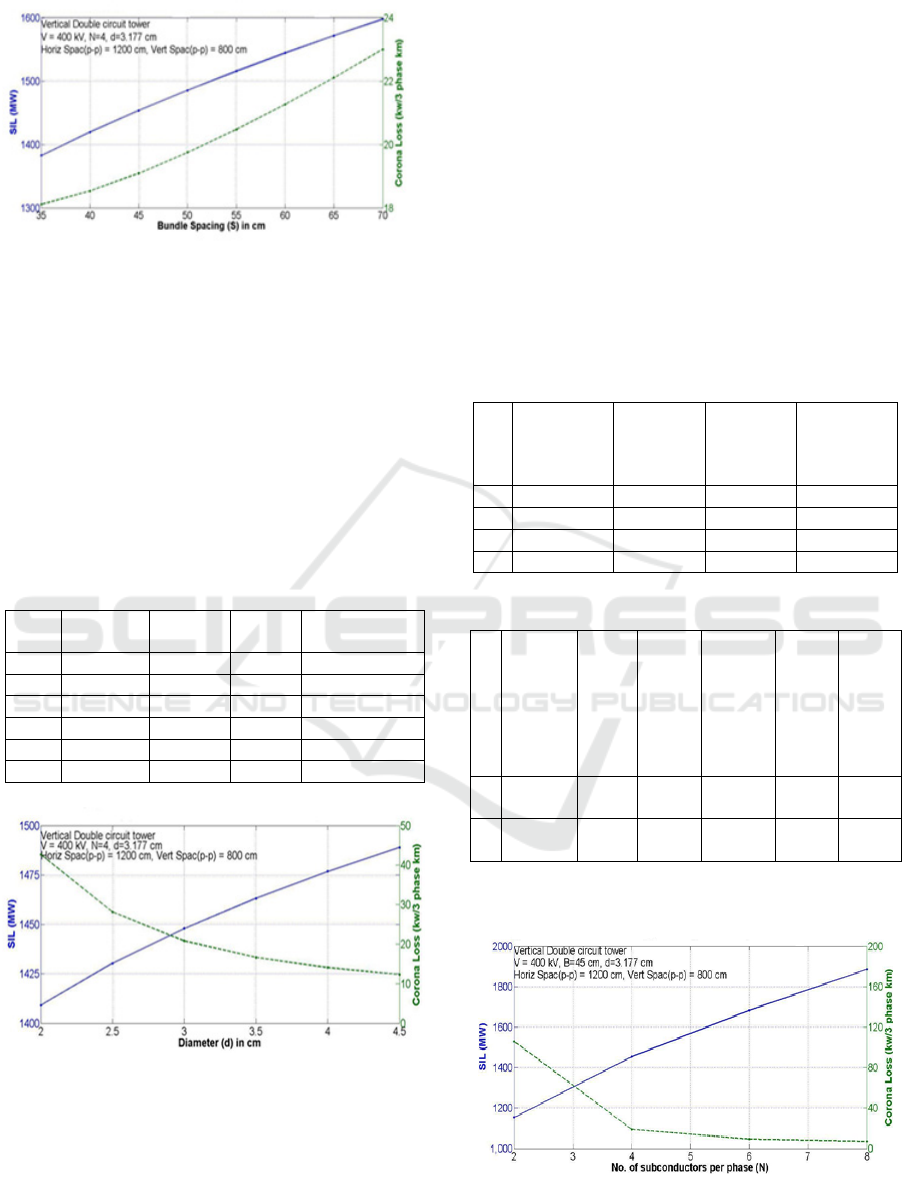
Figure 1: Bundle Spacing (B) v/s SIL and Corona

3.2 Size of Conductor (d)

The diameter of the conductor is the size of conductor,

with the increase in diameter of conductor the GMReq of

the conductor increases and self-inductance of the line

reduces, hence there is reduction in inductance of the line

and there is increase in SIL level. There would also be more

reduction in the corona loss is obtained with increase in

diameter of conductor. The Table 2 and Figure 2 show the

effect of change in diameter of conductor on SIL and corona

loss.

Table 2: Diameter of Conductor (d) in cm v/s SIL and

Corona

(

)

(

mH/km

)

(

nF/km

)

SIL

(

)

Pc(kw/3phase

)

2 0.381 29.62 1409.2 11.55

2.5 0.376 30.06 1430.2 11.76

3 0.371 30.44 1447.9 12.04

3.5 0.367 30.76 1463.2 12.37

4 0.364 31.05 1476.8 13.13

4.5 0.361 31.31 1488.9 13.55

Figure 2: Diameter of conductor (d) v/s SIL and Corona

3.2.1 No. of Sub-conductors per phase

(Bundle) (N)

The No. of sub-conductors in a bundle increases there

would be rise in the GMReq of the conductor which

would reduce self-inductance of the line, and

reduction in inductance of the line, therefore there

will be increment in SIL level. There is a large

increment in SIL level is obtained and current

carrying capacity also increases. Also corona loss

would reduce drastically with increase in N. However

increase in N the loading on existing transmission

tower increases so to reduce the weight we can shift

from twin ASCR moose conductor to quad ACSR

zebra conductor having reduced diameter and weight,

but still the overall weight on tower increases, so it is

possible only when from the tower is designed to

carry increases weight so that we can fulfil the

requirement of future increase in power demand. The

following Table 3,4 and Figure 3 shows the effect of

change in No. of sub conductors per phase on SIL.

Table 3: N v/s SIL and Corona

(mH/km)

(nF/km)

SIL

(MW)

(kw/

3phase

km)

2 0.469 24.38 1153.9 55.49

4 0.37 30.56 1453.63 12.04

6 0.319 35.32 1683.33 7.16

8 0.285 39.52 1885.39 5.95

Table 4: N v/s SIL and Corona (including weight and cost)

ACSR

Condu

ctor

diamet

er (cm)

Wei

ght

(kg/

km)

Appr

ox.

Cost

cond.

(Rs./

SIL

(MW)

Diffe

rence

(kw/

3phas

e km)

Moose

3.177

2004 300 1153.9 0 55.49

Zebra

2.862

1621 260 1443.4 289.5 13.71

Figure 3: No. of Sub-conductors per phase (N) v/s SIL and

Corona

Performance Analysis and Improvement of Double Circuit EHV AC Transmission Lines by Increasing Surge Impedance Loading Level

873

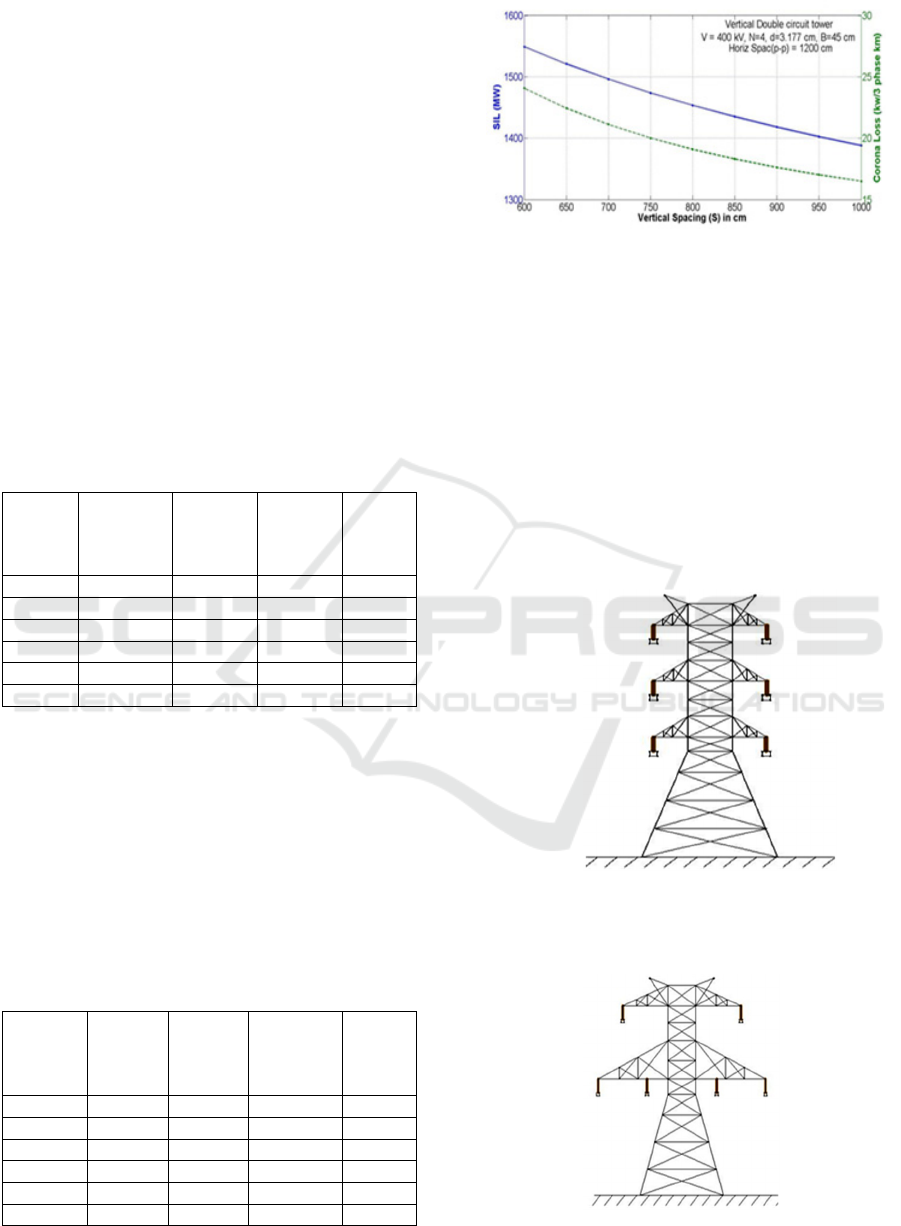
3.2.2 Horizontal Spacing

The phase to phase spacing is a factor of GMD

(Geometric Mean Distance), i.e. if the spacing

between conductors is reduced GMD will decrease

and there will be increase in mutual inductance of the

line which leads to reduction in line inductance and

increase in SIL level. However there is limit on the

spacing between conductors due to sag of the

conductors. This is due to the fact that more the sag

more is the swing of the conductor and there are

chances of p-p faults, but if we use V string insulators

or conductor is replaced with HTLS (high

temperature low sag conductors) eg. ACSS

(Aluminium Conductor Steel Supported) either both

the swinging of conductor is reduced and the spacing

of conductors can be reduced. The Table 5 and Figure

4 show the effect of change in spacing between the

bundles on SIL.

Table 5: P-P Spacing v/s SIL and Corona

P-P

spacin

g (m)

(mH/km)

(nF/km)

SIL

(MW)

(kw/3p

hase

km)

10 0.366 30.90 1469.80 12.63

11 0.368 30.72 1461.32 12.31

12 0.37 30.56 1453.63 12.04

13 0.372 30.41 1446.69 11.83

14 0.374 30.28 1440.43 11.66

15 0.375 30.16 1434.81 11.51

3.2.3 Vertical Spacing

The reduction in vertical spacing reduces GMD

which leads to increases in the SIL level. But we

cannot reduce this spacing much because we have to

see the spacing of conductor from tower as well as the

below crossarm. However we can reduce this spacing

till the voltage gradient and corona loss is within

limit. The Table 6 and Figure 5 show the effect of

change in vertical spacing between the phases on SIL.

Table 6: Vertical Spacing v/s SIL and Corona

Vertical

spacing

(m)

L(mH/k

(nF/km

)

SIL

(MW)

(kw/

3phase

)

7 0.36 31.46 1496.14 13.06

7.5 0.365 30.99 1473.83 12.51

8 0.37 30.56 1453.63 12.04

8.5 0.375 30.17 1435.19 11.65

9 0.379 29.81 1418.23 11.30

9.5 0.384 29.48 1402.53 11.01

Figure 5: Vertical Spacing v/s SIL and Corona

4 DOUBLE CIRCUIT

CONFIGURATIONS

The arrangement of conductors also affects the SIL.

The transmission line inductance can be reduced by

proper geometrical configuration of conductors. For

a 400kV Double circuit tower the configurations are

as shown in figure 6, 7, 8 and 9.

4.1 Vertical tower

Figure 6: Vertical tower

4.2 Delta tower

Figure 7: Delta tower

INCOFT 2025 - International Conference on Futuristic Technology

874

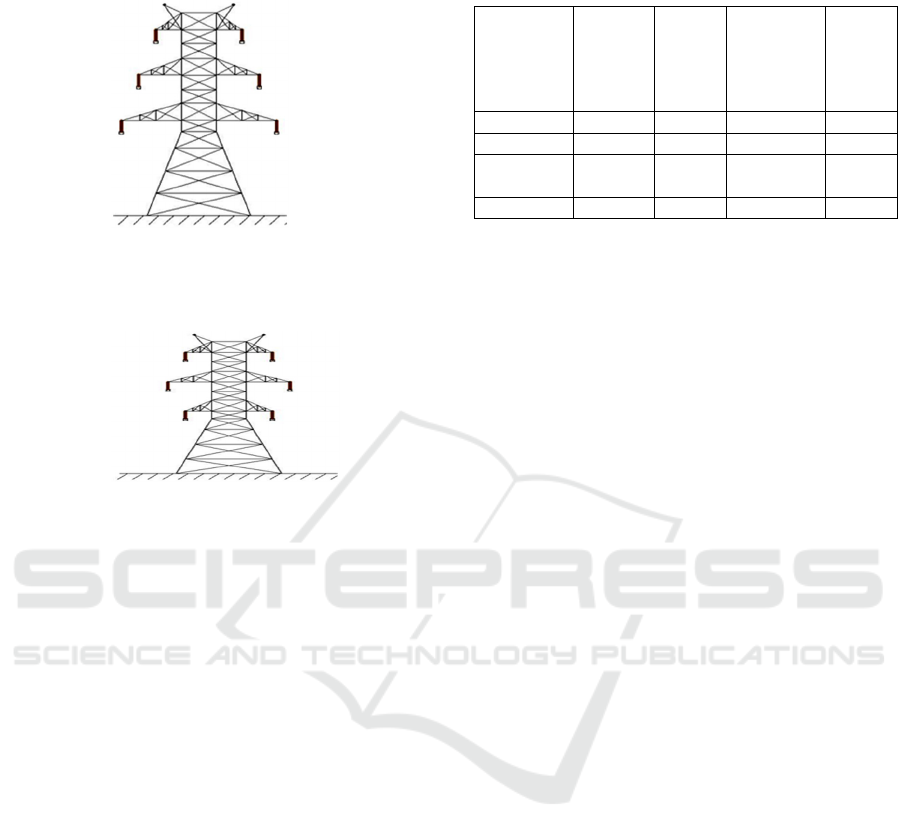
4.3 Inverted V tower

Figure 8: Inverted V tower

4.4 Hexagon tower

Figure 9: Hexagon tower

5 COMPARISON OF DOUBLE

CIRUCIT CONFIGURATIONS

Comparing Horizontal, Delta and L configuration

Towers in terms of SIL level for a specific given data

V = 400kV, N = 4, B = 45 cm, d = 3.177 cm

(moose conductor)

•

For vertical configuration S = 1200 cm (

horizontal p-p spacing), S = 800 cm

(Vertical p-p spacing)

•

For delta configuration Dhb = Dhy1 = 600

cm, Dhy = Dhr1 = 1400 cm, Dhr = Dhb1 =

1000 cm, Dvry = Dvbr = Dvy1b1 = Dvr1b1

= 692.82 cm, Dvyb = Dvr1y1 = 0 cm, Dry =

Dyb = Dbr = Dr1y1 = Dy1b1 = Db1r1 = 800

•

For Inverted V Configuration Dhr = Dhb1 =

600cm, Dhb = Dhr1 = 800 cm, Dhy = Dhy1

= 700 cm, Dvry = Dvyb = Dvr1y1 = Dvy1b1

= 800 cm, Dvbr = Dvr1b1 = 1600 cm

• For Hexagon configuration Dhr = Dhb1 =

Dhb = Dhr1 = 600cm, Dhy = Dhy1 = 800

cm, Dvry = Dvyb = Dvr1y1 = Dvy1b1 = 800

cm, Dvbr = Dvr1b1 = 1600 cm

Where, Dhr = Horizontal distance of R phase

from centre of tower, Dvry = Vertical distance

between R and Y phase.

Table 7: Comparison of various Double circuit line

configurations

Double

Circuit

Configura

tions

L(mH/

km)

C(nF/

km)

Fair

corona

loss

(kw/3phas

e km)

SIL

(MW)

Vertical 0.37 30.56 0.65 1453.6

Delta 0.365 31.04 0.65 1476.2

Inverted

0.374 30.25 0.64 1439.0

Hexagon 0.369 30.63 0.64 1456.9

5.1 Advantages of using Delta

configuration and Hexagon

Configuration over Vertical

• There is an increase of approx. 23 MW in

SIL for delta compared to Vertical.

• The advantage of using Delta

configuration is reduction in no. of cross

arm requirement. Also height of the tower

can be reduced using Delta tower

compared to vertical.

• There is no need for transposition of lines

as the spacing between the lines is

symmetrical, hence the voltage drop

would be equal among the lines.

• There is an increase of approx. 3.3 MW in

SIL for Hexagon compared to Vertical.

6 CONCLUSIONS

The power transmission capacity of long EHV AC

lines is limited by SIL/Stability limits due to the

presence of large inductance of the line. So by

reducing the inductance and hence inductive

reactance and surge impedance, the power transfer

capacity can be enhanced. The decrease in inductance

and surge impedance would increase SIL level. The

Various techniques to increase SIL level close to

thermal limit can be done by

• Reduction in spacing between conductors (p-

p),

• Increase in bundle spacing

• Increase in diameter of conductor

• Increase in no. of sub-conductors per phase

The comparison for EHV AC 400 kV double

circuit tower configurations have been done. The

double circuit configurations considered for

comparisons are Vertical, Hexagon, Inverted V, and

delta tower configuration. The delta and Hexagon

Configuration shows increment in SIL compared to

Performance Analysis and Improvement of Double Circuit EHV AC Transmission Lines by Increasing Surge Impedance Loading Level

875

vertical tower, as well as it is possible to reduce height

of tower. Hence it is possible to enhance the power

transfer capability by above different techniques.

REFERENCES

R. N. Nayak, Y K Sehgal and Subir Sen, “EHV

Transmission line capacity Enhancement through

increase in Surge Impedance Loading Level, Published

in Power India Conference, (2006 IEEE).

Jose R. Daconti and Daniel c. Lawry “Increasing Power

Transfer Capability of Existing Transmission Line”,

Published in Transmission and Distribution Conference

and Exposition, (2003 IEEE).

Jin Hao and Wilsun Xu, “Extended Transmission line

Loadability Curve by including Voltage Stability

Constraint”, Published in Electric Power Conference,

(2008 IEEE Xplore).

Kishore T.S; Singal S.K., “Design Economics of EHV

Power lines ”, Advances in Electrical Engineering

(ICAEE), 2014 international IEEE conference

publication.

Gaddam Siva, Priyanka Rani, Anubhav Tiwari, Aditya

Gaddam, “Methods, Merits and Demerits of Improving

Power Transfer Capability based on Voltage and Surge

Impedance”, International Journal of Engineering

Research & Technology, Vol. 3 Issue 3, March 2014,

ISSN : 2278-0181.

Aydin Sakhavati, Mostafa Yaltagiani, Shirin Saleh Ahari,

Seyed Mahdi Mahaei,“765 kV Transmission line

Design (Electrical Section)” International Journal of

Electrical and Computer Engineering (IJECE) Vol.2,

No.5, October 2012, pp. 698~707 ISSN: 2088-8708

Rakosh Das Begamudre, Extra High Voltage Ac

Transmission Engineering, 3

edition, New Delhi, New

Age International Publisher, (2006).

Hadi Saadat, Power System Analysis, McGraw Hill

Publisher (1999).

CEA yearly Report on Electricity Generation Review 2011-

2012.

Indian Standard IS 5613 (part 3) Code of Practice for

Design, Installation and Maintenance of 400kV

Overhead Power Lines.

Fajar Tri Wardana; Rudy Setiabudy, Study of Increasing

Surge Impedance Loading (SIL) and Voltage at

DEPOK Substation by Changing TASIK-DEPOK 500

kV Transmission Line's Configuration, at IEEE 2019

2nd International Conference on High Voltage

Engineering and Power Systems (ICHVEPS), October

01-04,2019, held at Denpasar, Indonesia.

Amir Lotfi; Mona Ghassemi, Smart Transmission

Expansion Planning Based on Unconventional High

Surge Impedance Loading Line Designs, at 2021 IEEE

Power & Energy Society Innovative Smart Grid

Technologies Conference (ISGT), February 16-18,

2021 held at Washington, DC, USA.

Jitendra Jamnani; Varun Patel, Surge Impedance Loading

level enhancement of 765 kV long EHV AC line

through bundle configurations, at IEEE 2016 Biennial

International Conference on Power and Energy

Systems: Towards Sustainable Energy (PESTSE),

January 21-23, 2016 held at Bengaluru, India.

Bhuban Dhamala; Mona Ghassemi, Transmission

Expansion Planning via Unconventional High Surge

Impedance Loading (HSIL) Lines, at 2023 North

American Power Symposium (NAPS), October 15-17,

2023 held at Asheville, NC, USA.

INCOFT 2025 - International Conference on Futuristic Technology

876